In-Trajectory Inverse Reinforcement Learning: Learn Incrementally From An Ongoing Trajectory

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it addresses a critical limitation in current Inverse Reinforcement Learning (IRL) methods—the inability to learn incrementally from ongoing trajectories. This opens up new avenues for real-time applications, such as robotics, human-computer interaction, and autonomous systems, where immediate feedback and adaptation are vital. The theoretical guarantees and empirical validation further strengthen its contribution, providing a solid foundation for future advancements in online IRL.

Visual Insights

#

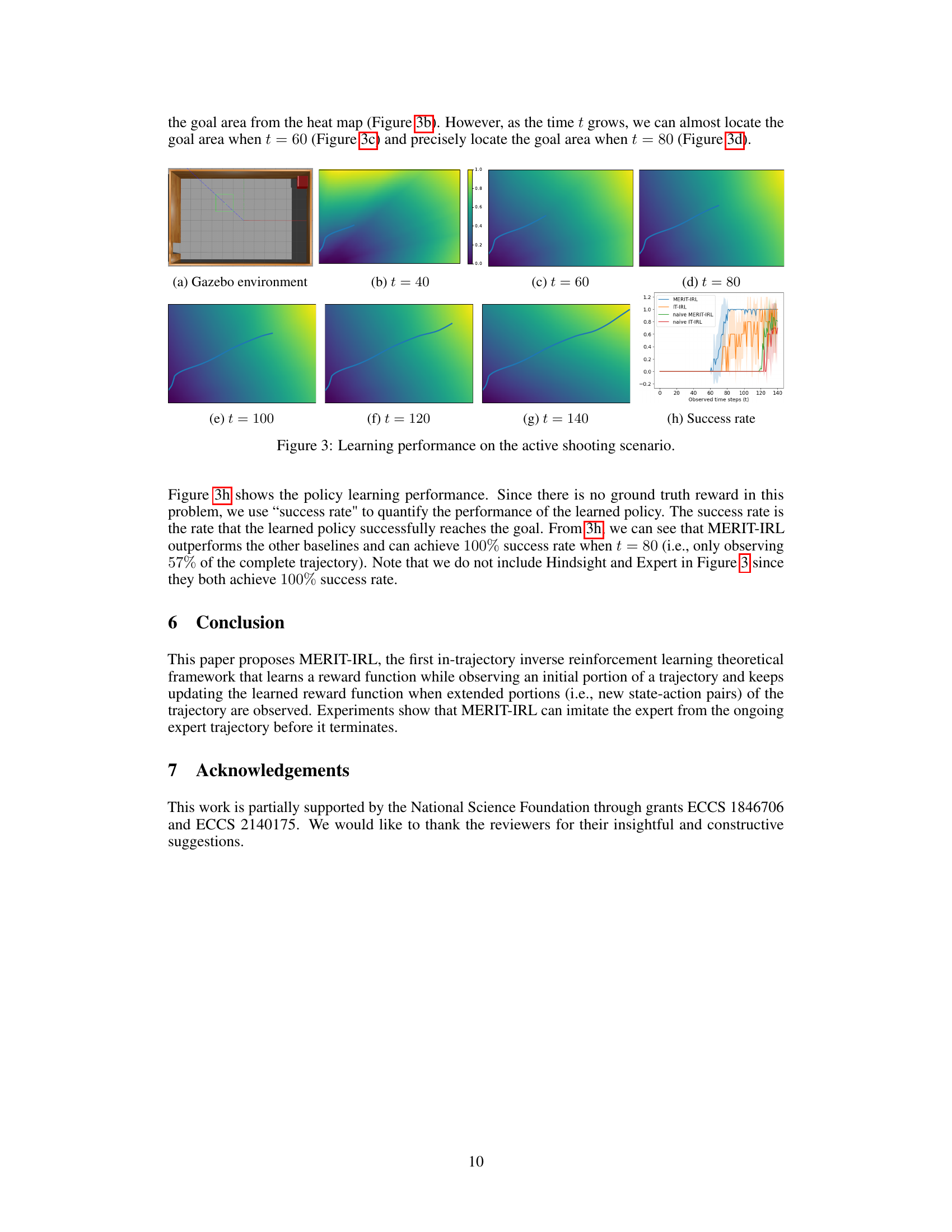
This figure visualizes three different approaches to reward updates in inverse reinforcement learning (IRL). The left panel shows the standard IRL method, which compares complete expert and learner trajectories. The middle panel illustrates a naive in-trajectory method, comparing only the trajectory prefixes up to the current time step. The right panel presents the proposed MERIT-IRL method, which creates a complete trajectory by combining the expert’s trajectory prefix with a learner-generated suffix, allowing for a comparison of complete trajectories even with incomplete data.

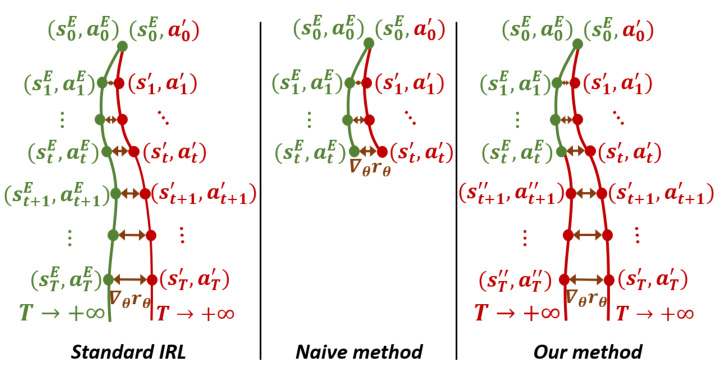
This table presents the quantitative results of four different in-trajectory inverse reinforcement learning algorithms (MERIT-IRL, IT-IRL, Naive MERIT-IRL, Naive IT-IRL) and two baselines (Hindsight and Expert) across four different tasks (HalfCheetah, Walker, Hopper, and Stock Market). For each task and algorithm, the mean and standard deviation of a performance metric (likely cumulative reward) are reported, calculated across 10 test runs. This allows for a comparison of the performance of each algorithm in various situations.

In-depth insights

#

In-trajectory IRL

#

In-trajectory Inverse Reinforcement Learning (IRL) presents a novel approach to learning reward functions and policies directly from ongoing trajectories. Unlike traditional IRL methods that require complete trajectories, In-trajectory IRL addresses the limitations of waiting for trajectory completion, especially crucial in scenarios demanding real-time adaptation. This method dynamically updates the reward and policy as new state-action pairs from an ongoing trajectory become available. The formulation of this problem as an online bi-level optimization problem is a significant contribution, enabling continuous learning and adaptation. The proposed algorithm, MERIT-IRL, incorporates a meta-regularization term to mitigate overfitting, given the limited data available in an ongoing trajectory. Furthermore, theoretical guarantees of sub-linear regret are provided, showcasing the algorithm’s efficiency and robustness. The experimental results on several tasks, including MuJoCo robotic control and stock market prediction, demonstrate the effectiveness of In-trajectory IRL and its ability to learn effectively from incomplete data, providing a significant advance in the field of IRL.

MERIT-IRL Algo

#

The MERIT-IRL algorithm is a novel approach to in-trajectory inverse reinforcement learning (IRL). It addresses the limitations of traditional IRL methods which require complete trajectories before learning can begin. This is achieved by formulating the learning process as an online bi-level optimization problem. The upper level dynamically updates the reward function based on newly observed state-action pairs from the ongoing trajectory, incorporating a meta-regularization term to prevent overfitting. The lower level, concurrently, updates the corresponding policy. The algorithm cleverly uses a single-loop approach, enhancing computational efficiency. Theoretically, MERIT-IRL is proven to achieve sub-linear regret, guaranteeing its effectiveness in online settings with temporally correlated data. The algorithm’s design is particularly suited for real-time applications where quick inference is crucial, such as in safety-critical situations involving ongoing actions.

Regret Bounds

#

Regret bounds are a crucial concept in online learning, quantifying the difference in performance between an algorithm’s choices and those of an optimal, clairvoyant algorithm. In the context of in-trajectory inverse reinforcement learning (IRL), regret bounds are particularly important because the learning happens incrementally on an ongoing trajectory, not a batch of complete trajectories. The paper focuses on minimizing the local regret, a metric appropriate for non-convex problems where global optimality is unattainable. The key result is demonstrating sub-linear regret bounds, meaning the algorithm’s cumulative loss grows sublinearly in the number of observed state-action pairs. Importantly, the authors prove a tighter bound (O(log T)) under the assumption of a linear reward function. These bounds provide theoretical guarantees for the algorithm’s performance, demonstrating its efficiency in learning even with limited and temporally correlated data. The analysis addresses the challenges of non-i.i.d. data inherent in this online setting. The meta-regularization technique used helps in achieving these favorable regret bounds by preventing overfitting to the limited available data. Therefore, the theoretical analysis strongly supports the practical effectiveness of their method in handling the complexities of in-trajectory IRL.

Meta-Regularization

#

The heading ‘Meta-Regularization’ hints at a crucial technique used to address the challenge of limited data in in-trajectory inverse reinforcement learning (IRL). Standard IRL methods often rely on complete expert trajectories for learning, a luxury not afforded in this setting where only an ongoing trajectory is observed. Meta-regularization acts as a form of prior knowledge injection, leveraging information from related, simpler tasks to guide the learning process. This is particularly clever because it mitigates overfitting, a severe threat when dealing with sparse data, by regularizing the reward function’s parameters. The meta-prior, learned from a set of similar auxiliary tasks, acts as a regularizer ensuring that the learned reward function remains within a reasonable range of previously observed ‘relevant experience’. This approach elegantly handles the temporal correlation of the data inherent in ongoing trajectories, a difficulty not typically encountered in offline IRL methods. By using a meta-regularization term, the model is less likely to overfit to a single, incomplete trajectory, thus improving its generalization ability and robustness.

Future Work

#

The paper’s conclusion mentions “future work” to address reward identifiability in the in-trajectory IRL setting. This is a crucial point because the current objective function focuses on aligning policy with expert demonstrations, not directly quantifying reward learning performance. Future research could explore methods to directly evaluate and analyze the learned reward function’s accuracy and generalizability. This might involve comparing the learned rewards to ground truth rewards (where available), developing novel metrics to assess reward quality, or establishing theoretical bounds on reward estimation error. Further investigation into the impact of the meta-regularization term on reward learning is also warranted. Understanding its effect on generalization and overfitting is key, especially when dealing with limited data. Finally, robustness analysis under various data conditions, especially noisy or incomplete trajectories, and different MDP structures would greatly strengthen the work. Extending the algorithm to handle more complex scenarios, such as multi-agent systems or continuous action spaces, while maintaining theoretical guarantees, represents another promising avenue for future research.

More visual insights

#

More on figures

This figure shows the in-trajectory learning performance of MERIT-IRL and other baselines on four different tasks: HalfCheetah, Walker, Hopper, and Stock Market. The x-axis represents the time step of the expert trajectory, and the y-axis represents the cumulative reward of the learned policy at each time step. The shaded areas indicate the standard deviation across 10 different runs of each algorithm. The figure demonstrates that MERIT-IRL achieves comparable performance to the expert policy using only partial trajectories, highlighting its ability to learn incrementally from ongoing trajectories. In contrast, the other baselines (IT-IRL, Naive MERIT-IRL, and Naive IT-IRL) struggle to match the expert’s performance without using the full trajectory. The Hindsight baseline, which uses the complete trajectory, serves as an upper bound for comparison.

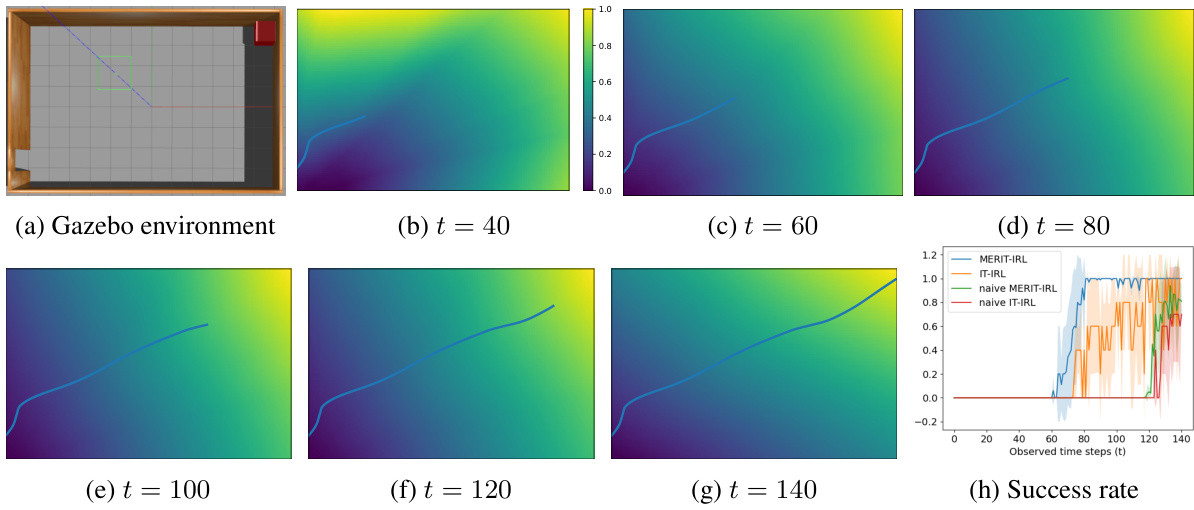
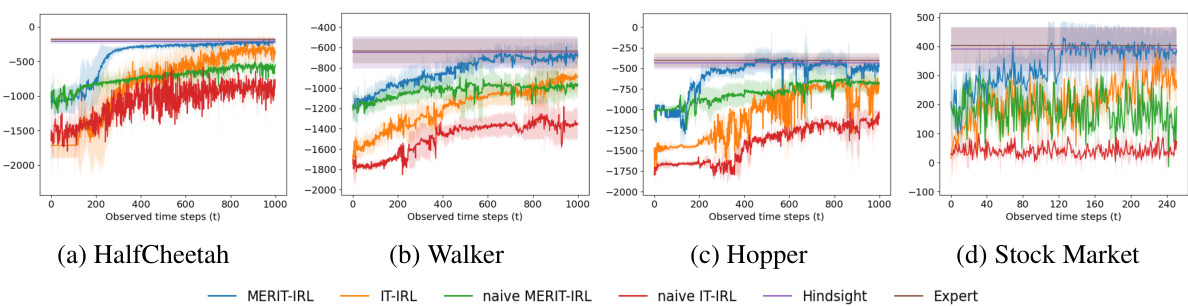
This figure visualizes the in-trajectory learning performance in an active shooting scenario. Subfigures (b) through (g) show heatmaps of the learned reward function at different time steps (t) during the ongoing trajectory. The heatmaps show how the learned reward function becomes more precise at locating the goal area over time. The trajectory of the shooter starts at the bottom left and ends at the top right. Subfigure (h) shows the success rate (the rate that the learned policy successfully reaches the goal) for different algorithms.

Full paper

#