TL;DR#
Inverse Optimization (IO) aims to infer the objective function of an agent’s decision-making process from observed data, but existing methods struggle with scalability and expressiveness, particularly for complex tasks with high-dimensional data. Traditional IO methods often rely on linear models, limiting their ability to capture complex relationships in real-world scenarios.
This paper introduces Kernelized Inverse Optimization (KIO), leveraging kernel methods to significantly improve the expressiveness of IO models and extending the hypothesis class to a reproducing kernel Hilbert space (RKHS). To tackle the computational challenges associated with the increased dimensionality of RKHS, the paper proposes a novel algorithm called Sequential Selection Optimization (SSO) to train KIO. SSO efficiently trains the KIO model by selectively updating parameters. Results show KIO and SSO improve efficiency and accuracy in learning from demonstration tasks, demonstrating promising results in low-data regimes on the MuJoCo benchmark.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the scalability issues in kernel methods for inverse optimization, a crucial problem in machine learning and AI. The proposed KIO model and SSO algorithm offer significant improvements in efficiency and scalability, allowing researchers to apply these techniques to larger and more complex problems, opening up new avenues of research and applications.
Visual Insights#

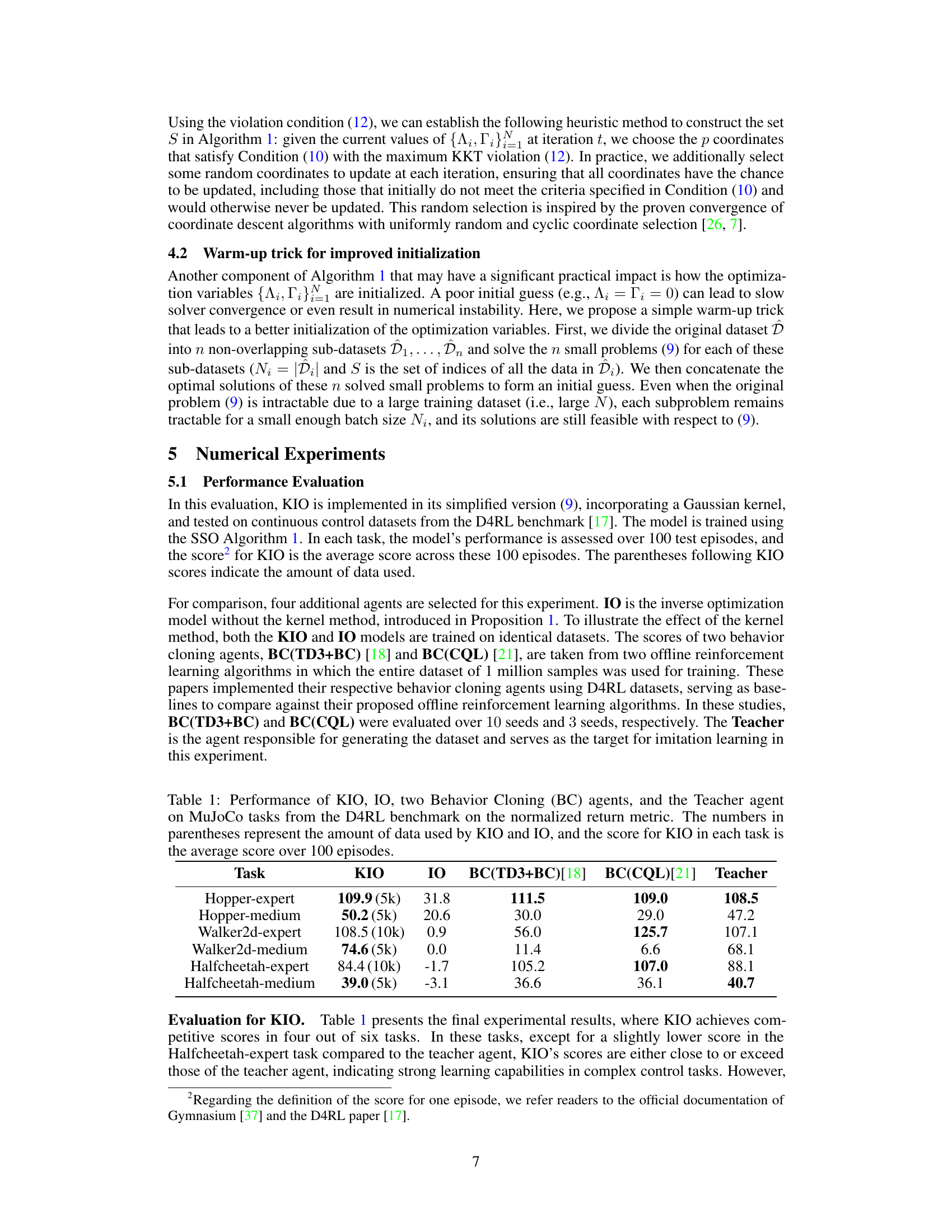
🔼 This figure shows the convergence curves for the Sequential Selection Optimization (SSO) algorithm across six different MuJoCo tasks from the D4RL benchmark. The x-axis represents the number of iterations, and the y-axis represents the error between the current objective function value and the optimal objective function value (calculated by SCS) in Problem (9). The plot demonstrates the fast convergence rate of the SSO algorithm, showing that errors for all tasks are below 0.1 by the 10th iteration and below 1e-4 by the 20th iteration.
read the caption
Figure 1: Convergence curves for SSO.

🔼 This table compares the performance of the proposed Kernel Inverse Optimization (KIO) model against other methods on six MuJoCo continuous control tasks from the D4RL benchmark. It shows the average normalized return for KIO (with varying dataset sizes), standard IO, two behavior cloning baselines (BC(TD3+BC) and BC(CQL)), and the expert (Teacher) agent for each task. The results highlight KIO’s ability to achieve comparable or better performance than existing methods, especially with limited data.
read the caption
Table 1: Performance of KIO, IO, two Behavior Cloning (BC) agents, and the Teacher agent on MuJoCo tasks from the D4RL benchmark on the normalized return metric. The numbers in parentheses represent the amount of data used by KIO and IO, and the score for KIO in each task is the average score over 100 episodes.
In-depth insights#
Kernel Inverse Opt#
Kernel Inverse Optimization (KIO) presents a novel approach to enhance inverse optimization by leveraging kernel methods. This extension allows for richer feature representations, moving beyond traditional finite-dimensional spaces to the infinite-dimensional space of a reproducing kernel Hilbert space (RKHS). The use of an RKHS significantly improves the model’s capacity to learn complex, non-linear relationships between decisions and objective functions. A key contribution is the development of a novel algorithm, Sequential Selection Optimization (SSO), which addresses the scalability challenges associated with traditional kernel methods, making KIO suitable for large datasets and complex tasks. The effectiveness of the KIO model, as well as SSO, is demonstrated through learning from demonstration tasks. This showcases the method’s ability to effectively learn complex decision-making behaviors from limited data and achieve strong generalization performance. This framework holds promise for diverse applications where inferring underlying decision-making objectives is crucial.
SSO Algorithm#
The paper introduces the Sequential Selection Optimization (SSO) algorithm as a crucial method to address the scalability challenges inherent in the proposed Kernel Inverse Optimization (KIO) model. SSO’s core innovation lies in its coordinate descent approach, selectively updating subsets of decision variables during each iteration, unlike traditional methods that update all variables simultaneously. This strategy significantly reduces computational complexity, making KIO applicable to large datasets. The algorithm’s efficiency is further enhanced by heuristics for selecting coordinates to update, prioritizing those with the most significant violation of the KKT conditions. A warm-up trick further improves the algorithm’s convergence speed. Experimental results demonstrate SSO’s effectiveness in achieving near-optimal solutions efficiently, outperforming direct SDP solvers in terms of speed and memory usage, particularly when dealing with large datasets. While the paper provides empirical evidence of SSO’s efficacy, a theoretical analysis of its convergence properties would strengthen its contribution, providing deeper insights into its performance and behavior under various conditions. Despite the lack of rigorous theoretical guarantees, SSO’s practical effectiveness makes it a valuable tool for large-scale inverse optimization problems.
MuJoCo Results#
A hypothetical ‘MuJoCo Results’ section would likely present empirical evidence demonstrating the effectiveness of the proposed Kernel Inverse Optimization (KIO) approach. This could involve comparisons against baseline methods (e.g., behavior cloning, standard inverse optimization) across multiple MuJoCo benchmark tasks. Key performance metrics such as average reward, success rate, or task completion time would be reported, showing how KIO outperforms existing algorithms, especially in low-data regimes. The results would ideally include visualizations such as plots showing learning curves across various tasks, illustrating the convergence speed and generalization capabilities of the KIO model. Crucially, the analysis should highlight the impact of the algorithm’s key components, such as the kernel method and the proposed Sequential Selection Optimization (SSO), demonstrating the benefits of each in improving performance and scalability. The results would ideally control for hyperparameters and random seeds, providing statistical significance measures to support the claims of improved performance and robustness of KIO. Finally, a discussion of any unexpected results or limitations observed in the MuJoCo experiments could offer valuable insights into the strengths and weaknesses of the proposed methodology.
Scalability Issues#
The inherent scalability challenges in kernel methods, particularly within the context of inverse optimization, are a significant concern. High dimensionality in feature spaces, coupled with the computational cost of solving kernel-based optimization problems (often involving quadratic complexity), severely limits the applicability of such methods to large datasets. This limitation is directly addressed by the introduction of the Sequential Selection Optimization (SSO) algorithm. SSO’s strategic approach, selectively updating subsets of coordinates during each iteration, effectively tackles the computational burden. The algorithm leverages coordinate descent principles and the structure of the optimization problem to achieve significant computational gains. The practical implication is that SSO enables the application of kernel inverse optimization techniques to considerably larger datasets than previously feasible, expanding the scope and impact of the methodology.
Future Works#
Future research directions stemming from this Kernel Inverse Optimization (KIO) work could explore several promising avenues. Improving the scalability of the SSO algorithm remains a key priority, potentially through investigating more sophisticated coordinate selection strategies or exploring alternative optimization techniques. Theoretical analysis of the SSO algorithm’s convergence rate is needed to provide stronger guarantees on its efficiency and performance. Extending KIO to handle different types of loss functions beyond suboptimality loss could enhance its applicability to a broader range of problems. Finally, evaluating KIO on more complex real-world problems with high-dimensional state and action spaces would rigorously assess its generalization capabilities and robustness in realistic settings. A comparative analysis against other state-of-the-art imitation learning approaches would further solidify KIO’s position within the field.
More visual insights#
More on tables
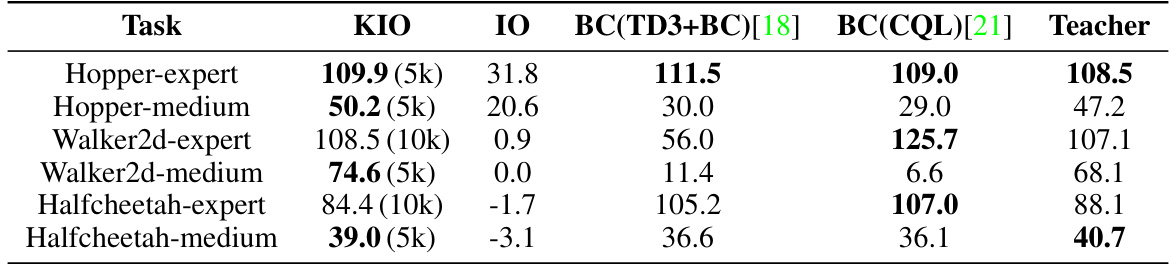
🔼 The table presents the performance comparison of six different agents (KIO, IO, BC(TD3+BC), BC(CQL), and Teacher) across six different MuJoCo tasks from the D4RL benchmark. The normalized return metric is used to evaluate the performance, and for KIO and IO, the amount of training data used is specified in parentheses. KIO’s scores represent the average over 100 test episodes.
read the caption
Table 1: Performance of KIO, IO, two Behavior Cloning (BC) agents, and the Teacher agent on MuJoCo tasks from the D4RL benchmark on the normalized return metric. The numbers in parentheses represent the amount of data used by KIO and IO, and the score for KIO in each task is the average score over 100 episodes.
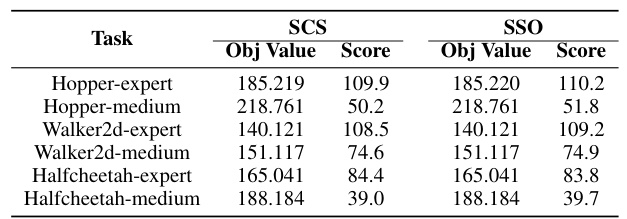
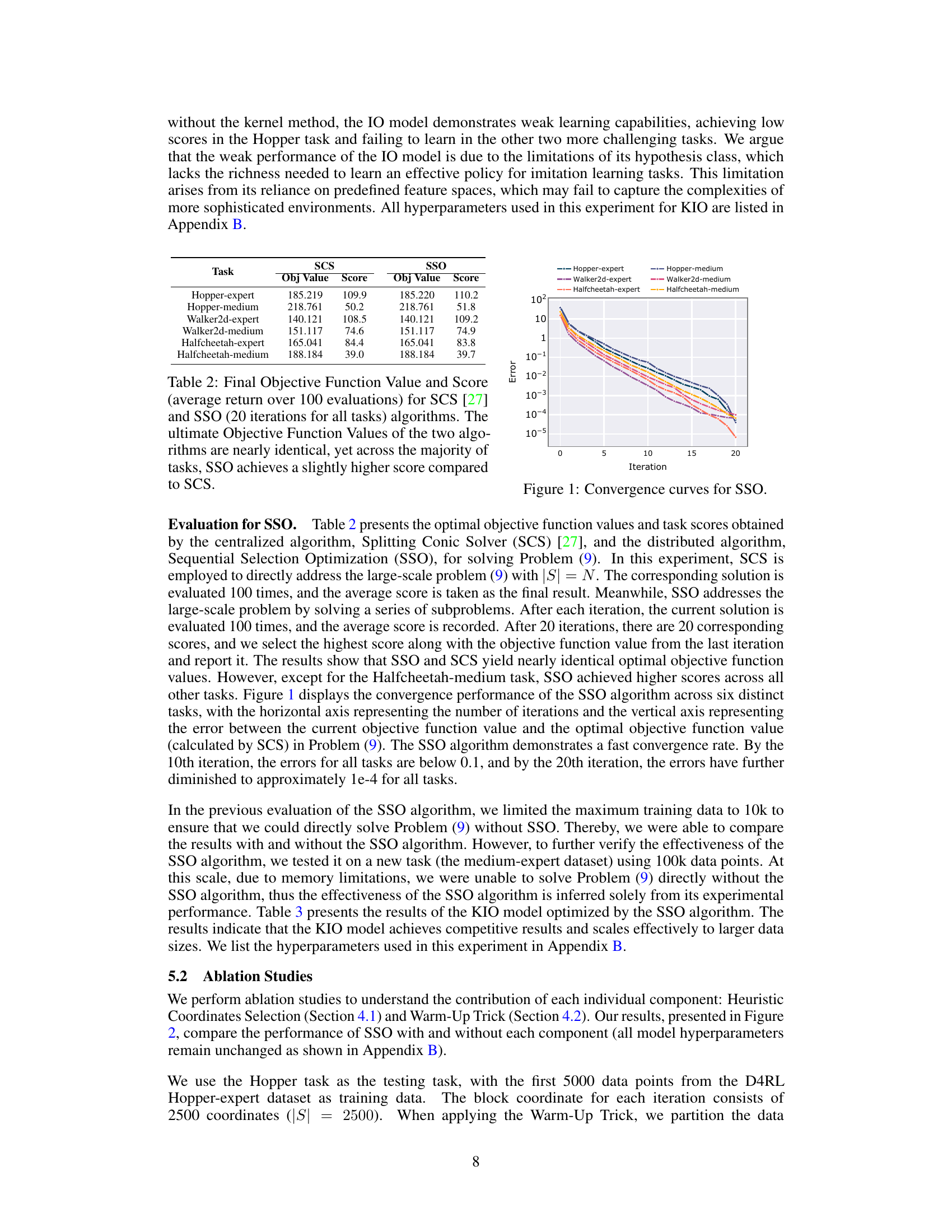
🔼 This table compares the performance of two algorithms, SCS and SSO, in solving the optimization problem (9) from the paper. The comparison is based on the objective function value and the average score (return) over 100 test episodes for six different tasks. It shows that while both algorithms achieve very similar objective function values, SSO generally achieves slightly better scores (higher average return).
read the caption
Table 2: Final Objective Function Value and Score (average return over 100 evaluations) for SCS [27] and SSO (20 iterations for all tasks) algorithms. The ultimate Objective Function Values of the two algorithms are nearly identical, yet across the majority of tasks, SSO achieves a slightly higher score compared to SCS.

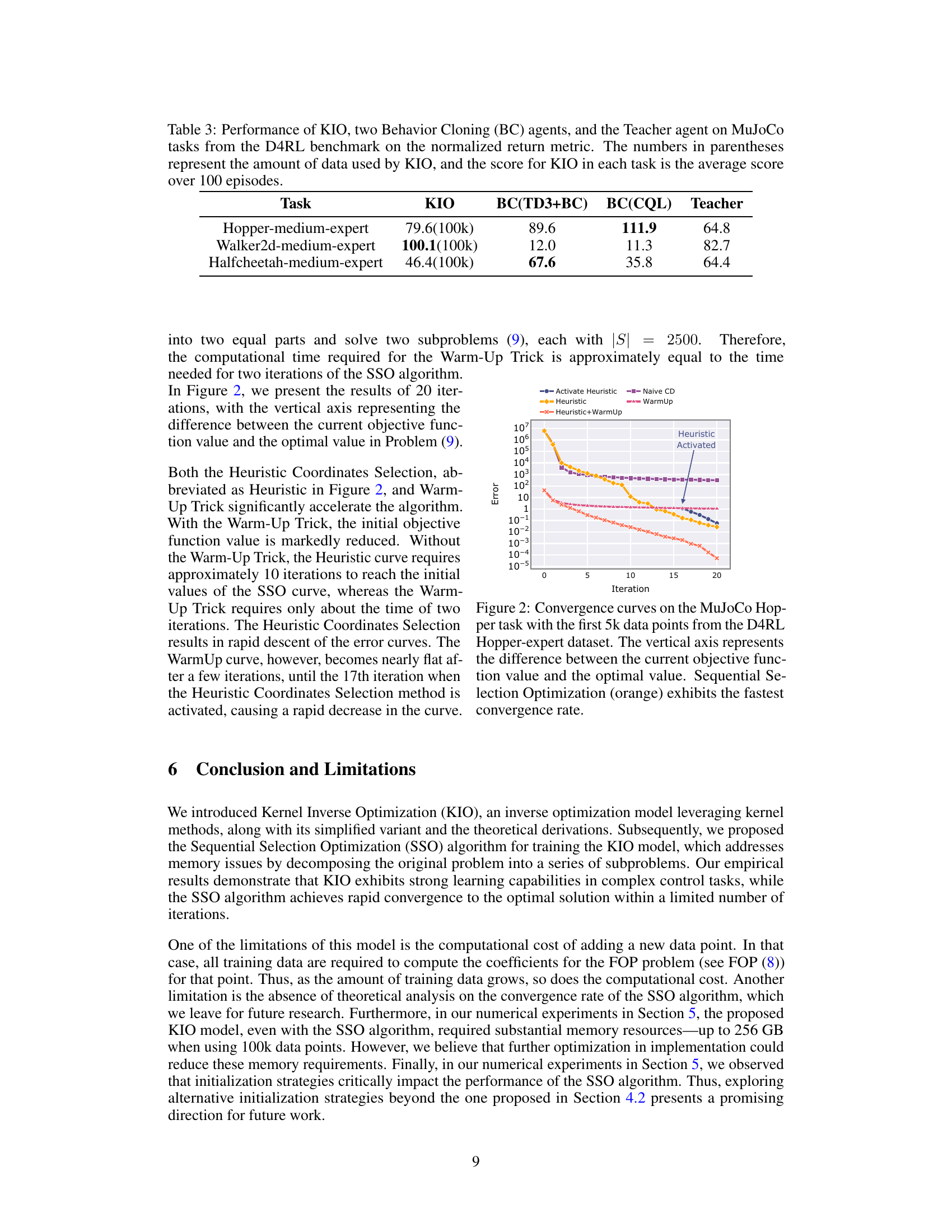
🔼 This table presents the performance comparison of the proposed Kernel Inverse Optimization (KIO) model against two behavior cloning baselines (BC(TD3+BC) and BC(CQL)) and a teacher agent on three MuJoCo tasks from the D4RL benchmark. The KIO model’s scores represent the average normalized return over 100 test episodes, with the number of data points used in parentheses. The table highlights KIO’s performance, particularly when compared to the behavior cloning baselines.
read the caption
Table 3: Performance of KIO, two Behavior Cloning (BC) agents, and the Teacher agent on MuJoCo tasks from the D4RL benchmark on the normalized return metric. The numbers in parentheses represent the amount of data used by KIO, and the score for KIO in each task is the average score over 100 episodes.
🔼 This table presents a comparison of the performance of five different agents on six MuJoCo tasks from the D4RL benchmark. The agents are Kernel Inverse Optimization (KIO), Inverse Optimization (IO), two behavior cloning agents (BC(TD3+BC) and BC(CQL)), and the Teacher agent (which generated the dataset). The table shows the average normalized return for each agent on each task, with the number of data points used by KIO and IO indicated in parentheses. The results demonstrate the relative performance of KIO against other methods, particularly highlighting the advantage of the kernel method in achieving high scores.
read the caption
Table 1: Performance of KIO, IO, two Behavior Cloning (BC) agents, and the Teacher agent on MuJoCo tasks from the D4RL benchmark on the normalized return metric. The numbers in parentheses represent the amount of data used by KIO and IO, and the score for KIO in each task is the average score over 100 episodes.

🔼 This table presents the performance of the Kernel Inverse Optimization (KIO) model using different kernel functions (RBF, Laplace, and Linear) on various MuJoCo tasks from the D4RL benchmark. The scores represent the average normalized return over 100 test episodes, and error bars (standard deviation) are included to show variability.
read the caption
Table 5: Performance of KIO on MuJoCo tasks from the D4RL benchmark on the normalized return metric. The scores in each task represent the average score over 100 episodes within the range of one standard deviation.
Full paper#