TL;DR#
Decentralized learning, where multiple agents collaboratively train a model without a central coordinator, is gaining traction. However, existing methods often rely on explicit regularization (e.g., LASSO) which may affect performance. Furthermore, communication overhead in decentralized settings can be a significant bottleneck. This paper focuses on decentralized sparse regression, a problem similar to training deep learning models but simpler to analyze.
This paper addresses these challenges by analyzing the implicit regularization of Decentralized Gradient Descent (DGD) applied to a nonconvex, unregularized least squares formulation. The authors demonstrate that under specific conditions (good network connectivity, small initialization, and early stopping), DGD converges to the statistically optimal solution. They further propose a communication-efficient version (T-DGD) that achieves similar statistical accuracy but with logarithmic communication complexity. Numerical experiments validate the effectiveness of both DGD and T-DGD.
Key Takeaways#
Why does it matter?#
This paper is important because it provides theoretical guarantees for decentralized sparse regression, a problem with significant practical applications. It also introduces T-DGD, a communication-efficient algorithm, which is crucial for large-scale decentralized learning. The findings challenge existing beliefs about decentralized optimization and open new avenues for research on implicit regularization and communication efficiency.
Visual Insights#
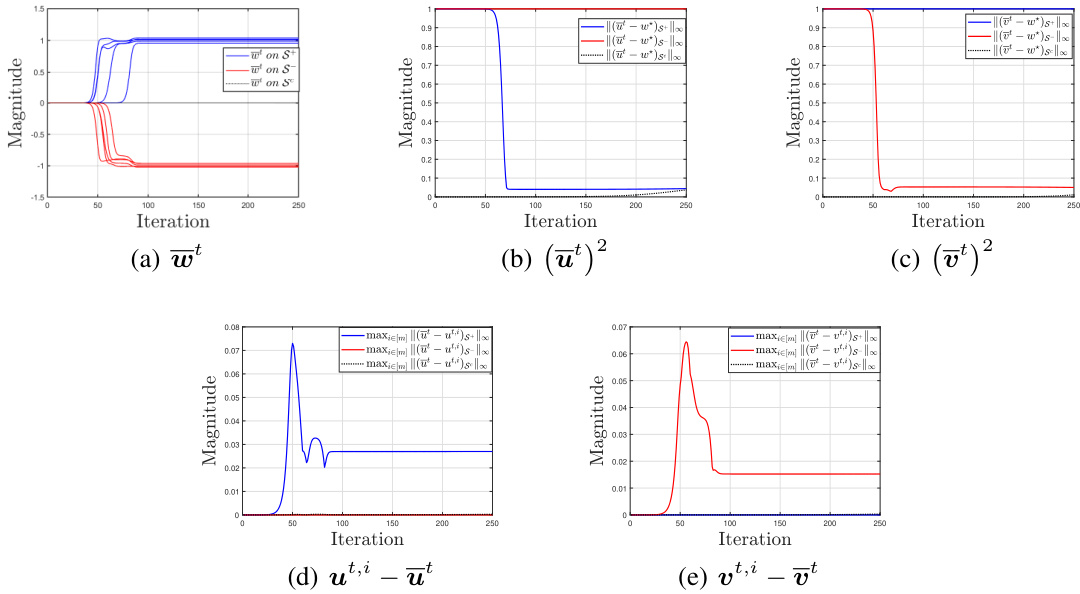
🔼 This figure visualizes the dynamics of averaged variables (w, u, v) and consensus errors (ut,i - ut, vt,i - vt) in DGD. Panel (a) shows the convergence of the averaged w, demonstrating successful convergence of elements on support S and maintenance of small magnitudes for elements on non-support Sc. Panels (b) and (c) illustrate how DGD utilizes u and v to fit parameters on positive and negative support, respectively. Panels (d) and (e) show the consensus errors, which correspond to the magnitudes of the model parameters, affirming the validity of the analysis.
read the caption
Figure 1: Dynamics of averaged variables and consensus errors.
In-depth insights#
Implicit Regularization#
Implicit regularization is a fascinating phenomenon in machine learning, particularly relevant in overparameterized models. It refers to the implicit constraints or biases imposed by the optimization algorithm itself, rather than explicitly defined regularizers like L1 or L2 penalties. Instead of adding regularization terms to the loss function, implicit regularization leverages the characteristics of the optimization process—such as gradient descent and its specific initialization and stopping criteria—to guide the model towards solutions with desirable properties, like sparsity or low-rankness. This often leads to better generalization and prevents overfitting, even when the model has far more parameters than data points. The paper focuses on decentralized settings, investigating how implicit regularization impacts the convergence and statistical guarantees of decentralized gradient descent (DGD) in sparse regression. A key insight is that under certain conditions, DGD can implicitly achieve statistically optimal solutions without explicit regularization, relying on careful initialization and early stopping. This finding challenges the conventional wisdom that explicit regularization is always required for decentralized sparse learning, suggesting potentially more efficient and communication-friendly approaches to decentralized learning. Furthermore, the study introduces a truncated DGD (T-DGD) algorithm to enhance the communication efficiency of DGD while retaining good statistical performance.
Decentralized DGD#
Decentralized Gradient Descent (DGD) is a fundamental algorithm in distributed machine learning, aiming to train models across multiple agents without a central server. In the context of sparse regression, decentralized DGD presents unique challenges and opportunities. The non-convex nature of the loss function in overparameterized sparse regression makes convergence analysis particularly difficult. Unlike centralized approaches, decentralized DGD must contend with communication constraints and the inherent heterogeneity among agents. One key advantage of DGD in this setting is the potential for implicit regularization, where the algorithm implicitly biases towards sparse solutions without requiring explicit regularization terms, leading to better generalization. However, convergence guarantees for decentralized DGD are often weaker than their centralized counterparts, typically only establishing convergence to a neighborhood of a solution, rather than the global optimum. Furthermore, communication efficiency is a critical consideration in decentralized training. The cost of transmitting data across agents can significantly impact overall performance. Consequently, research focusing on decentralized DGD for sparse regression often includes efforts to improve communication efficiency, such as through model compression or tailored communication protocols.
Truncated DGD#
The proposed Truncated Decentralized Gradient Descent (T-DGD) algorithm addresses the communication bottleneck inherent in high-dimensional decentralized optimization. Standard DGD requires transmitting high-dimensional vectors at each iteration, leading to significant communication overhead. T-DGD cleverly mitigates this by truncating the vectors, retaining only the s elements with the largest magnitudes (where s is the sparsity level). This significantly reduces communication complexity to a logarithmic dependence on the ambient dimension d, achieving communication efficiency without substantial loss of statistical accuracy. Theoretical analysis demonstrates that under specific conditions (sufficient samples, high signal-to-noise ratio, good network connectivity), T-DGD achieves comparable statistical accuracy to the standard DGD. This method demonstrates the practical advantages of implicit regularization in decentralized sparse regression, particularly in high-dimensional settings. The truncation strategy is a key innovation that strikes a balance between communication efficiency and statistical performance, overcoming limitations of existing decentralized sparse regression methods that lack such efficiency or suffer from polynomial dependence on d. Numerical experiments validate the theoretical findings, showcasing T-DGD’s effectiveness in achieving optimal statistical accuracy with substantially lower communication cost.
Statistical Optimality#
The concept of statistical optimality in the context of decentralized sparse regression focuses on achieving the best possible statistical accuracy given the constraints of a distributed system. It signifies that the algorithm’s output (a sparse model) is statistically close to the true underlying model that generated the data. The challenge lies in achieving this optimality while dealing with the inherent limitations of decentralized computations, including communication constraints and potential for error accumulation across multiple agents. Therefore, demonstrating statistical optimality requires establishing both statistical error bounds and convergence rate analysis for the decentralized algorithm, especially in the high-dimensional regime where the number of features exceeds the available data samples. Implicit regularization, where sparsity emerges as a byproduct of the optimization process rather than through explicit penalty terms, plays a crucial role in this context. The analysis would also need to consider the effects of network topology and the interaction between local and global error terms. Ultimately, proving statistical optimality offers a strong theoretical guarantee, suggesting that the method is not only efficient but also reliable for recovering sparse models from limited and distributed data.
Communication Efficiency#
The concept of communication efficiency is central to decentralized machine learning, particularly when dealing with high-dimensional data. In decentralized settings, agents need to exchange information, and the communication overhead can significantly impact performance. This paper tackles this challenge by introducing a communication-efficient version of the decentralized gradient descent algorithm (DGD) called T-DGD. T-DGD achieves this efficiency by truncating the iterates before transmission, keeping only the ’s’ elements with the largest magnitudes. This truncation reduces the communication cost, making it logarithmic in the ambient dimension ’d’. The paper theoretically demonstrates that T-DGD achieves comparable statistical accuracy to DGD in high signal-to-noise ratio (SNR) regimes, while significantly reducing communication overhead. This is a crucial finding because it addresses a major bottleneck in decentralized learning, enabling more scalable and practical implementations, especially when dealing with very large models. The logarithmic dependence on ’d’ is a significant improvement over existing decentralized sparse regression methods, which often have polynomial dependence. However, the effectiveness of T-DGD is dependent on sufficient sample size and high SNR, suggesting limitations in low-data or noisy environments. The practical implications are substantial, offering a pathway towards efficient decentralized learning of large-scale sparse models.
More visual insights#
More on figures

🔼 This figure shows the effects of ambient dimension (d) and initialization scale (α) on the performance of the Decentralized Gradient Descent (DGD) algorithm. Subfigure (a) and (b) illustrate how DGD achieves optimal statistical error across varying dimensions (d = 400, 4000, 40000) and network connectivity (ρ = 0.1778 and ρ = 0.7519). The plots display the log of the error (||wt - w*||2) versus the number of iterations. The dashed lines represent the optimal statistical error obtained in a centralized setting. Subfigure (c) demonstrates the influence of different initialization scales (α = 10-1 to 10-5) on the performance, showing that a small initialization is crucial for achieving optimal results.
read the caption
Figure 2: Impact of ambient dimension d and initialization α.

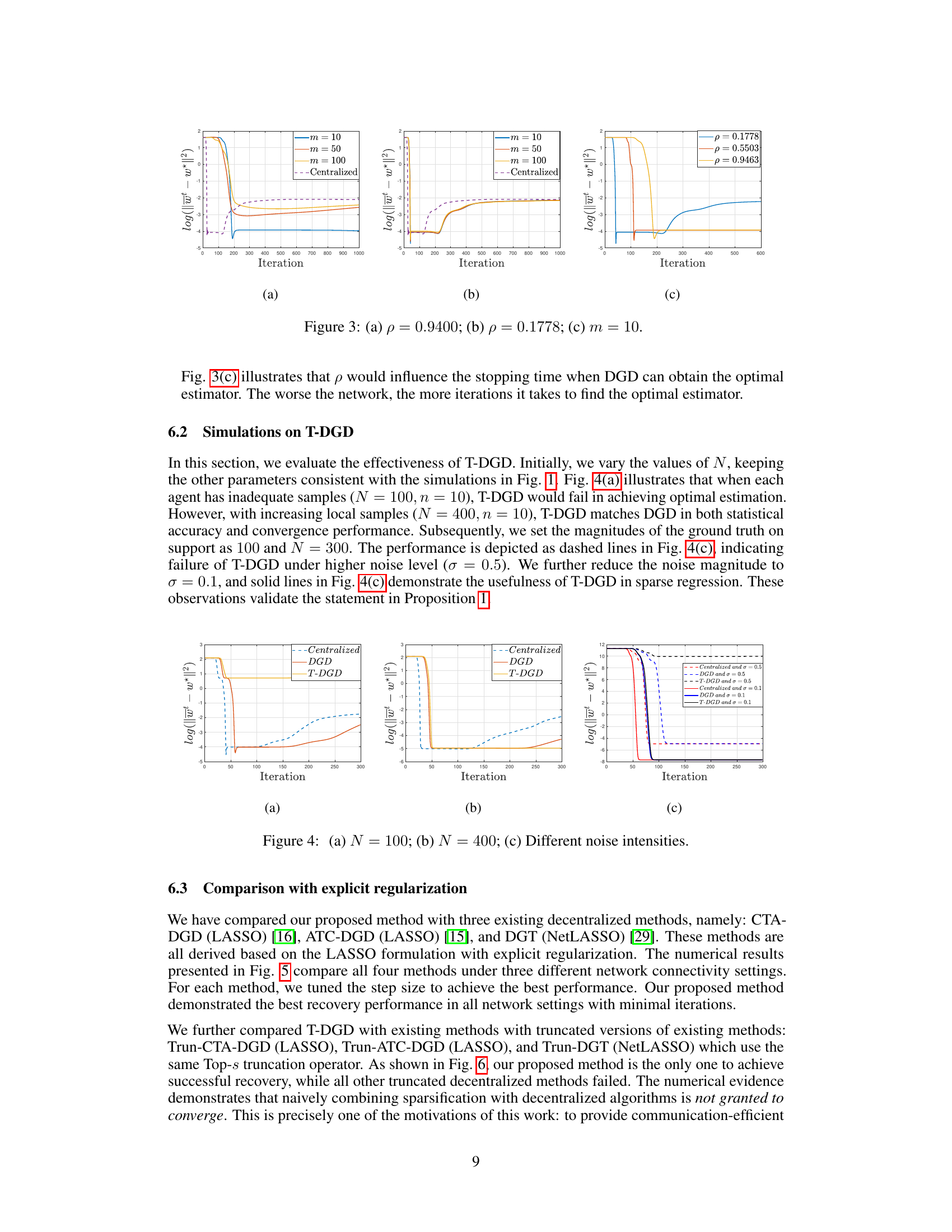
🔼 This figure shows the impact of network connectivity (ρ) and the number of agents (m) on the performance of the decentralized gradient descent (DGD) algorithm. Subfigure (a) shows the performance for a poorly connected network (ρ = 0.9400) with varying numbers of agents (m = 10, 50, 100) compared to the centralized setting. Subfigure (b) shows the performance for a well-connected network (ρ = 0.1778) with varying numbers of agents. Subfigure (c) shows the performance for a fixed number of agents (m = 10) with varying network connectivity. The y-axis represents the log of the error between the decentralized solution and the true solution. The x-axis represents the number of iterations.
read the caption
Figure 3: (a) ρ = 0.9400; (b) ρ = 0.1778; (c) m = 10.
🔼 This figure visualizes the dynamics of averaged variables and consensus errors in the decentralized gradient descent (DGD) algorithm. Subfigures (a) to (c) show the convergence of averaged variables (w, u, v), demonstrating successful convergence for elements on the support set S and maintenance of small magnitudes for those on the non-support set Sc. Subfigures (d) and (e) illustrate the consensus errors (ut,i − ūt, vt,i − ūt), showing trends corresponding to model parameter magnitudes, validating the analysis. The plots demonstrate how DGD effectively identifies the support of the sparse model parameter while controlling consensus errors.
read the caption
Figure 1: Dynamics of averaged variables and consensus errors.
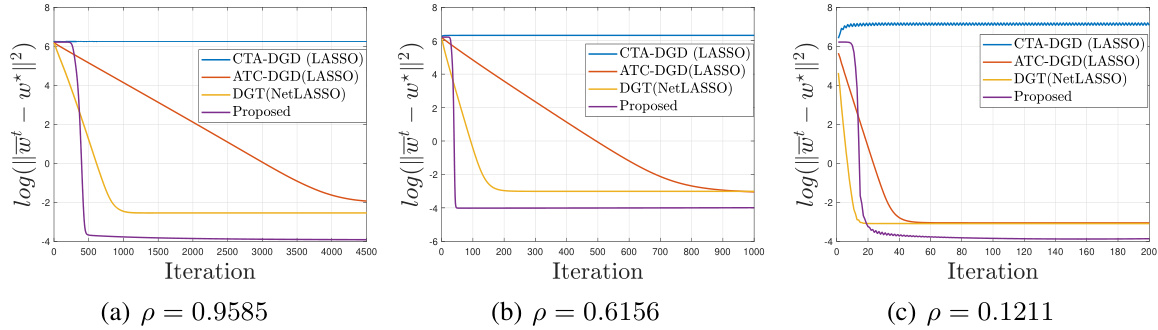
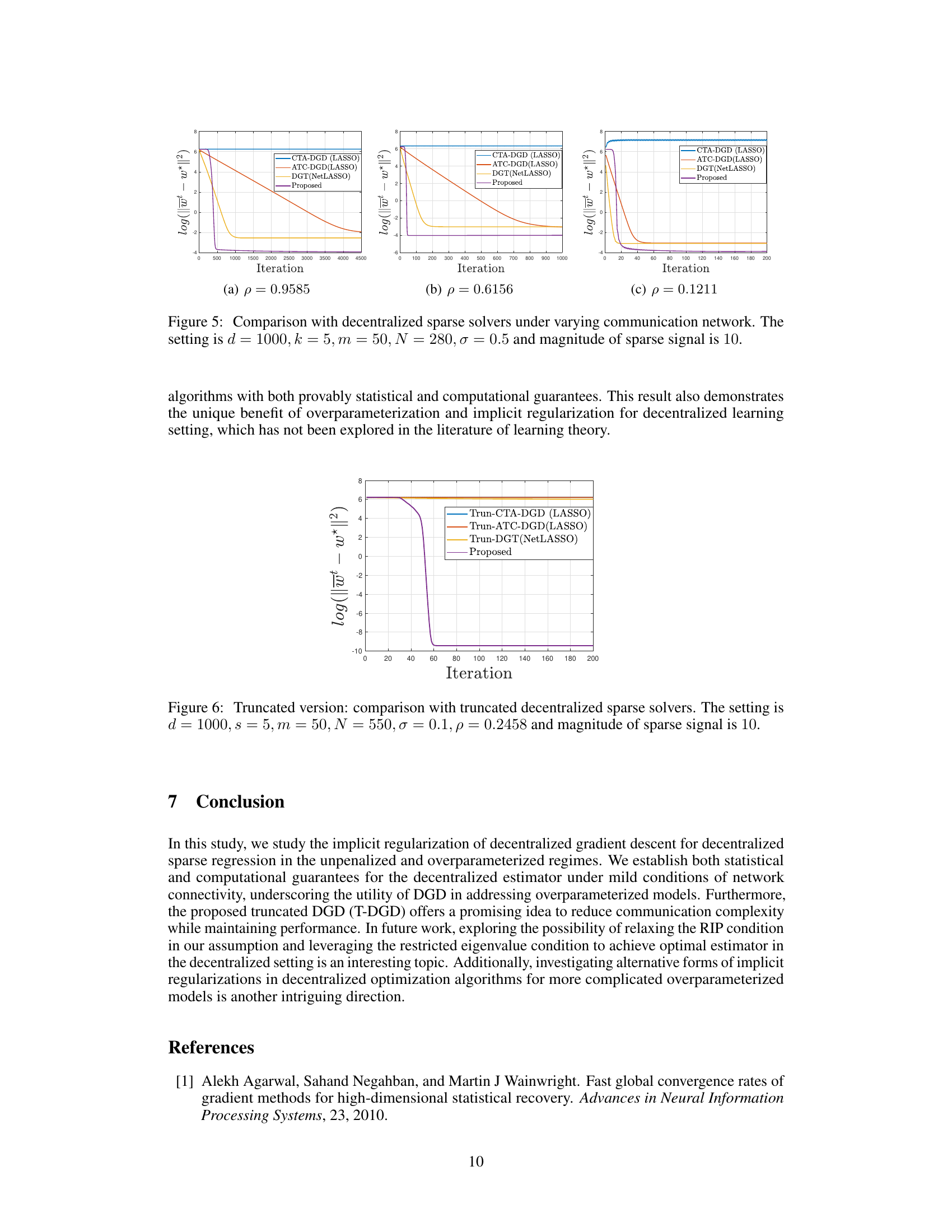
🔼 This figure compares the performance of four different decentralized sparse regression solvers under varying network connectivity conditions. The solvers are CTA-DGD (LASSO), ATC-DGD (LASSO), DGT (NetLASSO), and the proposed method. The x-axis represents the number of iterations, and the y-axis represents the log of the l2 error between the estimated sparse vector and the ground truth sparse vector. The figure shows that the proposed method outperforms the others, especially in scenarios with poor network connectivity.
read the caption
Figure 5: Comparison with decentralized sparse solvers under varying communication network. The setting is d = 1000, k = 5, m = 50, N = 280, σ = 0.5 and magnitude of sparse signal is 10.
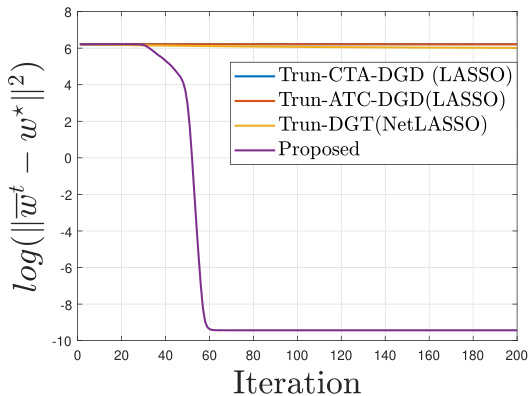
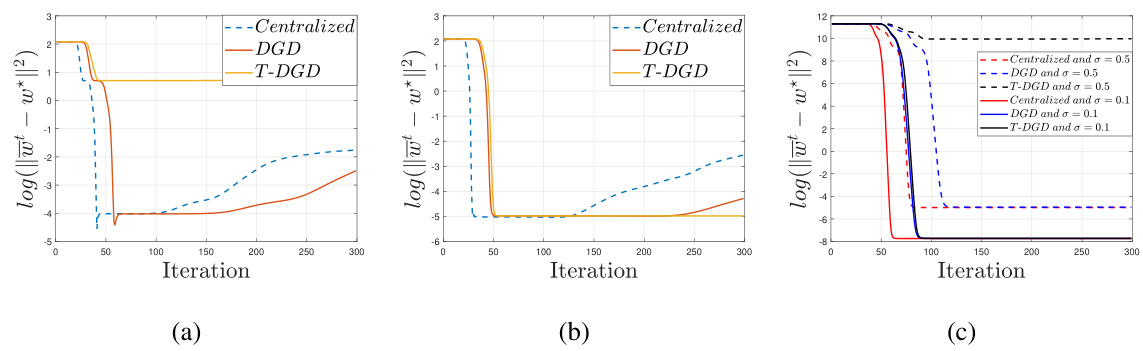
🔼 This figure compares the performance of the proposed Truncated Decentralized Gradient Descent (T-DGD) method with three other truncated decentralized methods for solving the decentralized sparse regression problem. The setting involves a high-dimensional problem (d=1000) with a relatively small number of non-zero elements (s=5), a moderate number of agents (m=50), a sample size (N=550), low noise (σ=0.1), moderate network connectivity (p=0.2458), and a signal-to-noise ratio high enough to ensure successful recovery by T-DGD. The results demonstrate the superiority of the proposed T-DGD method over the other methods in achieving successful recovery.
read the caption
Figure 6: Truncated version: comparison with truncated decentralized sparse solvers. The setting is d = 1000, s = 5, m = 50, N = 550, σ = 0.1, p = 0.2458 and magnitude of sparse signal is 10.
Full paper#