TL;DR#
Training deep learning models efficiently requires effective data sampling strategies. Current approaches often rely on heuristics or extensive, time-consuming trials. This limits their applicability, especially for large datasets. Furthermore, existing learning-based methods are computationally expensive and struggle to scale effectively.
Swift Sampler (SS) tackles these issues by introducing a novel, low-dimensional sampler formulation. This enables efficient automatic sampler learning using a fast approximation method, significantly reducing computational costs. SS demonstrates notable improvements in model accuracy across various datasets and network architectures, highlighting its adaptability and effectiveness.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on data sampling techniques for deep learning. It offers a novel and efficient method to automatically learn effective samplers, addressing the limitations of existing methods. This has significant implications for improving model training efficiency and performance, particularly on large-scale datasets. The proposed method, Swift Sampler (SS), is adaptable and can be applied across various neural networks. The work opens new avenues for research into automatic optimization and efficient hyperparameter search within the context of deep learning training.
Visual Insights#

🔼 This figure shows the effectiveness of the Swift Sampler (SS) in identifying and discarding noisy instances. Subfigure (a) displays the density of noisy instances in a 2D feature space defined by the loss and renormed entropy (Er). Subfigure (b) shows the sampling probabilities assigned by the SS sampler to the same instances. The comparison reveals that SS accurately identifies noisy instances (primarily located in areas with high loss and low Er) and significantly reduces their sampling probability.
read the caption
Figure 1: A demonstration of the effectiveness of our SS. (a) The density of noisy instances of noise 40% on CIFAR10 in (Loss,E') space. (b) The sampling probability of sampler from SS. (a)(b) show that SS accurately distinguishes the noisy instances and discards them.

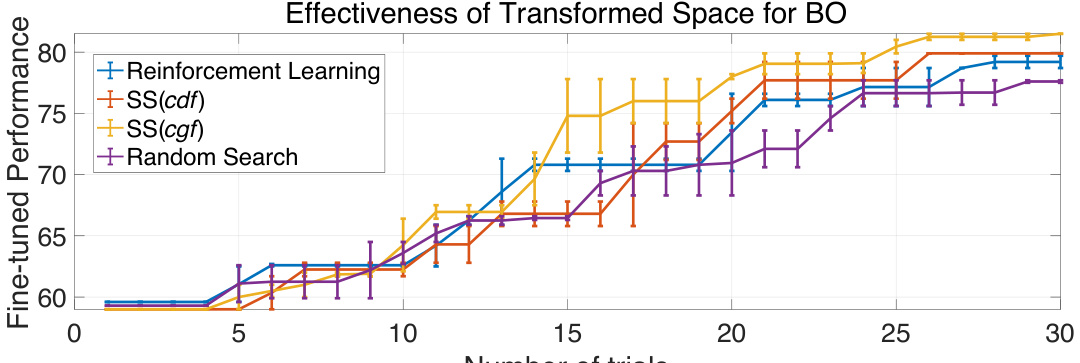
🔼 This table presents a comparison of the performance of the proposed Swift Sampler (SS) method against several other baseline methods on two image classification datasets, CIFAR-10 and CIFAR-100. The results are shown for different levels of added noise to the training data (0%, 10%, 20%, 30%, and 40%). Each entry shows the Top-1 accuracy on CIFAR-10 and CIFAR-100 respectively. The table helps demonstrate the robustness and effectiveness of the proposed SS method in handling noisy data.
read the caption
Table 1: SS results on CIFAR10 and CIFAR100 comparisons with other methods. The number pair X / Y means the Top-1 accuracy on CIFAR10 is X% and on CIFAR100 is Y%.
In-depth insights#
Swift Sampler#
The concept of a ‘Swift Sampler’ in a deep learning context suggests an algorithm designed for efficient data selection during model training. It likely addresses the challenge of navigating a massive dataset by strategically selecting a subset of training examples, rather than processing the entire set. This approach aims to accelerate training and improve model performance by focusing on the most informative samples. The ‘swift’ aspect likely implies low computational cost and fast convergence, perhaps achieved through innovative sampling strategies or efficient optimization techniques. A key aspect would be the algorithm’s ability to generalize across various datasets and model architectures, learning effective sampling procedures without extensive hyperparameter tuning or manual intervention. The efficiency gains would be crucial for large-scale datasets, where exhaustive sampling is computationally prohibitive. Automatic sampler learning is a core component, suggesting the algorithm adapts and improves its sampling strategy based on the characteristics of the training data and feedback from the training process. This adaptability distinguishes it from simpler, fixed sampling rules.
SS Optimization#
The heading ‘SS Optimization’ likely refers to the optimization strategy employed within the Swift Sampler (SS) algorithm. This process is critical, as it involves efficiently searching the vast space of possible samplers to identify one that significantly improves model performance. The core of SS optimization likely involves a bilevel optimization approach: an outer loop using Bayesian Optimization to search for the optimal sampler parameters, and an inner loop that efficiently approximates the model’s performance under a given sampler, avoiding costly full training cycles. Dimensionality reduction techniques were probably employed to make the sampler search tractable, likely by mapping the sampler to a low-dimensional space of hyperparameters. Smoothness techniques, such as modifying the objective function, were almost certainly used to mitigate the challenges posed by a potentially high-dimensional, sharp objective function landscape. The effectiveness of the SS optimization process would hinge on the carefully chosen sampler formulation, its ability to generalize across different model architectures and datasets, and the efficiency of the approximation method used within the inner loop to evaluate sampler performance. Overall, the efficiency and effectiveness of this optimization are key to the Swift Sampler’s ability to automatically learn high-performing data samplers for training deep learning models.
Sampler Design#
Effective sampler design is crucial for efficient deep learning. The paper’s approach focuses on automatic sampler search, moving beyond heuristic rules and time-consuming manual trials. A key innovation is the low-dimensional parameterization of the sampler, enabling efficient exploration of the search space using Bayesian Optimization. This contrasts with previous methods which often dealt with high-dimensional spaces, making optimization computationally expensive. The authors address challenges such as the sharpness of the objective function with a novel smoothing technique and the high cost of sampler evaluation through a fast approximation method. These design choices allow the algorithm to effectively search for optimal samplers even on large-scale datasets, resulting in significant performance improvements. The transferability of learned samplers across different network architectures is another noteworthy aspect of the proposed design.
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims and hypotheses presented. A strong empirical results section will typically include a detailed description of the experimental setup, including the datasets used, the evaluation metrics employed, and a clear comparison of the proposed method with existing baselines. Visualizations such as tables, charts, and graphs are essential for presenting the data in a clear and concise manner, allowing readers to easily grasp the performance differences. The discussion of results should go beyond simply stating the numbers; it should offer an analysis of trends, outliers, and potential sources of error. Statistical significance should be addressed, highlighting whether observed improvements are statistically sound or merely due to random chance. A comprehensive results section will also discuss the limitations of the experiments and suggest directions for future work. A robust empirical results section builds confidence in the validity and reliability of the research findings, ultimately strengthening the paper’s overall contribution to the field.
Future Works#
The “Future Works” section of a research paper on efficient sampler learning would naturally explore avenues for improvement and expansion. A promising direction would be investigating more sophisticated optimization algorithms beyond Bayesian Optimization to potentially accelerate the search process and discover even more effective samplers. Another key area is extending the sampler framework to diverse data modalities, beyond images, to explore applications in natural language processing, time-series analysis, or other domains. The development of theoretical guarantees for the proposed method would lend increased credibility and understanding. This includes providing a more rigorous analysis of its convergence properties and establishing bounds on its performance. Finally, robustness analysis could be enhanced to evaluate the sampler’s performance under different noise levels and dataset characteristics, making it more practical for real-world applications. In-depth exploration of these areas would solidify the contributions and open exciting new research possibilities.
More visual insights#
More on figures

🔼 This figure visualizes the sampler learned by the Swift Sampler (SS) method on the ImageNet dataset. Panel (a) shows example image crops that were assigned the lowest sampling probabilities by the learned sampler. These crops often contain irrelevant objects or are poorly positioned. Panel (b) presents a plot showing the relationship between the sampling probability and the cumulative distribution function (CDF) of the loss values for different ResNet model sizes. The plot demonstrates how the sampler prioritizes training examples with intermediate loss values, avoiding both easy and extremely difficult examples.
read the caption
Figure 2: Visualization of the sampler searched on ImageNet ILSVRC12: (a) The cropped images (in yellow boxes) with the least sampling probability in the sampler from SS. Most of them are in inappropriate positions and contain irrelevant objects. (b) The sampling probability of sampler from SS.
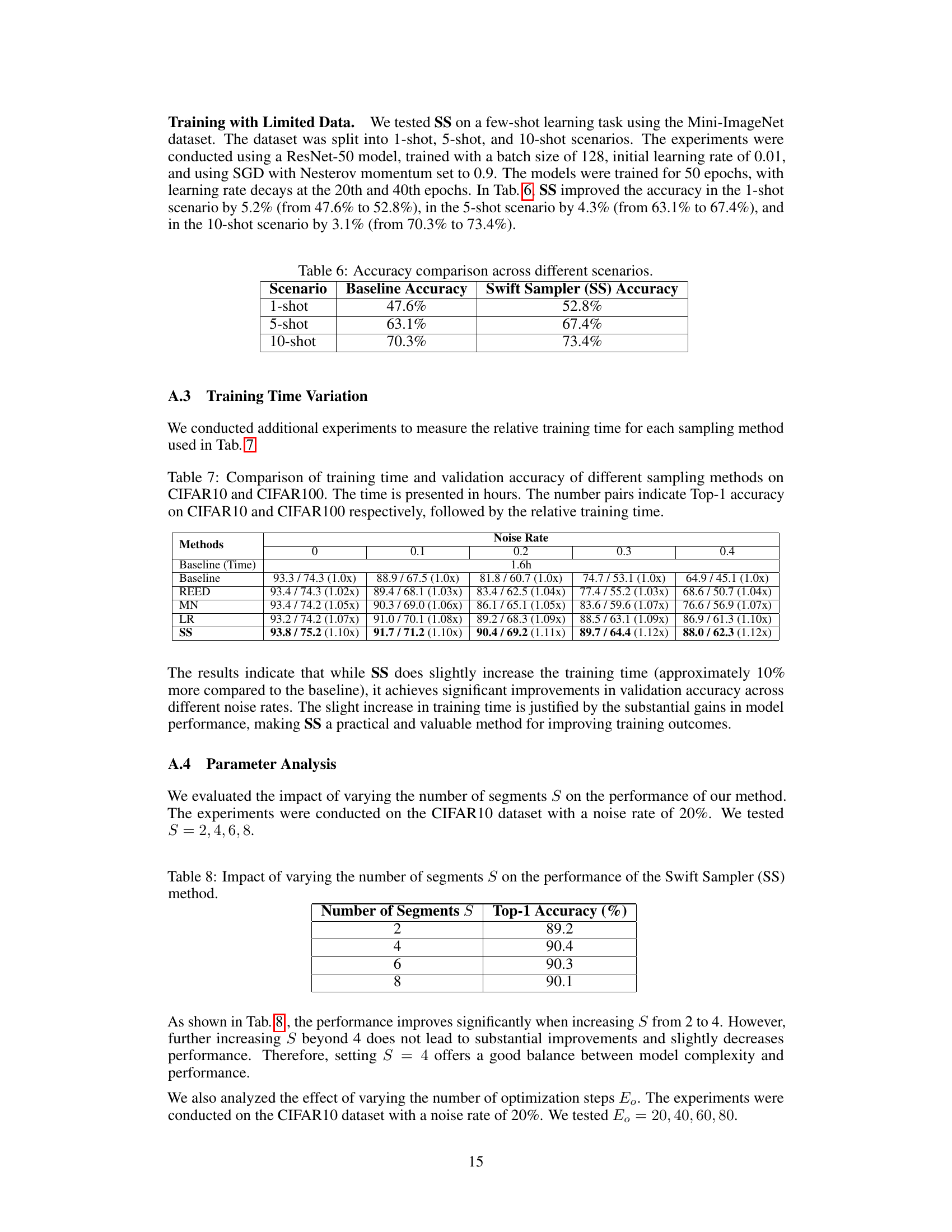
🔼 The figure shows the effectiveness of the proposed Swift Sampler (SS) method compared to other optimization methods (Reinforcement Learning, SS with cumulative distribution function (cdf), and random search). It demonstrates that SS using the cumulative gradient function (cgf) for transforming the objective function space leads to faster convergence and better performance than other methods on ImageNet.
read the caption
Figure 3: Verification of the efficiency of BO and the effectiveness of cgf in smoothing the OF. On ImageNet ILSVRC12, SS(cdf) outperforms RL as its estimation of the whole landscape of OF. SS(cgf) optimize faster than SS(cdf) as it smooths the OF.
More on tables
🔼 This table presents the performance comparison of the proposed Swift Sampler (SS) method with other existing methods on CIFAR-10 and CIFAR-100 datasets under various levels of label noise (0%, 10%, 20%, 30%, and 40%). The performance is measured by the Top-1 accuracy on each dataset. The table shows that the SS method consistently outperforms other methods, especially in high-noise scenarios.
read the caption
Table 1: SS results on CIFAR10 and CIFAR100 comparisons with other methods. The number pair X / Y means the Top-1 accuracy on CIFAR10 is X% and on CIFAR100 is Y%.

🔼 This table compares the Top-1 and Top-5 accuracy of the proposed Swift Sampler (SS) method against a baseline on the ImageNet ILSVRC12 dataset using various model architectures. It shows the consistent improvement in Top-1 accuracy achieved by SS across different models, with a smaller improvement in Top-5 accuracy.
read the caption
Table 2: Comparison of Top-1/5 accuracy of SS and baseline on ImageNet ILSVRC12. “MB”,“RN” and “SRN” means MobileNet ResNet and SE-ResNext. SS(self), SS(R18) and SS(R50) means the the sampler is searched on the target model, ResNet-18 and ResNet-50. All results are averaged over 5 runs, and the deviations are omitted because they are all less than 0.10. It is observed that SS has consistent improvements on Top-1 Acc on all cases, and the performance gain on Top-5 is relatively less because we only use Top-1 Acc as the objective of sampler search.

🔼 This table presents the comparison of verification performance between the proposed Swift Sampler (SS) method and the baseline method on two datasets: MS1M (train set) and YTF (test set). The performance is measured using ResNet-50 and ResNet-101 models. The table shows that SS consistently improves the performance compared to the baseline, demonstrating its effectiveness in face recognition tasks.
read the caption
Table 3: Comparision of verification performance % of SS and baseline on train set MS1M and test set YTF.
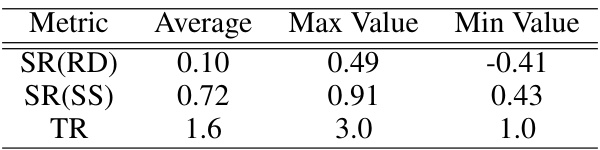
🔼 This table presents a comparison of the performance of the Swift Sampler (SS) method against baseline and other methods (REED, MN, LR) on CIFAR10 and CIFAR100 datasets with varying noise levels (0%, 10%, 20%, 30%, 40%). The results are presented as Top-1 accuracy pairs (CIFAR10/CIFAR100) for each method and noise level. It showcases the improved performance of SS, particularly in the presence of noisy labels.
read the caption
Table 1: SS results on CIFAR10 and CIFAR100 comparisons with other methods. The number pair X / Y means the Top-1 accuracy on CIFAR10 is X% and on CIFAR100 is Y%.

🔼 This table presents the performance comparison between the baseline uniform sampling method and the proposed Swift Sampler (SS) method on a large-scale dataset. The comparison is made across three key metrics: Top-1 accuracy, Top-5 accuracy, and convergence speed. Top-1 accuracy represents the percentage of correctly classified images in the top prediction. Top-5 accuracy refers to the percentage of images with the correct class label among the top 5 predictions. Convergence speed is expressed as a percentage relative to the baseline method, indicating how much faster the SS method converged compared to the baseline.
read the caption
Table 5: Performance comparison of different sampling methods.

🔼 This table shows the accuracy comparison between the baseline model and the Swift Sampler (SS) model across three different few-shot learning scenarios: 1-shot, 5-shot, and 10-shot. The scenarios refer to the number of training examples per class used for learning. The baseline accuracy represents the performance of a model trained without the Swift Sampler. The Swift Sampler (SS) accuracy shows the model’s performance after implementing the proposed SS method for data sampling during training.
read the caption
Table 6: Accuracy comparison across different scenarios.

🔼 This table presents the performance comparison of the proposed Swift Sampler (SS) method with other baseline methods (Baseline, REED, MN, LR) on CIFAR10 and CIFAR100 datasets under various noise levels (0%, 10%, 20%, 30%, 40%). The results are expressed as Top-1 accuracy pairs (CIFAR10/CIFAR100) and the relative training time compared to the baseline method for each noise level. The table highlights the superior performance of the SS method across different noise conditions.
read the caption
Table 1: SS results on CIFAR10 and CIFAR100 comparisons with other methods. The number pair X / Y means the Top-1 accuracy on CIFAR10 is X% and on CIFAR100 is Y%.

🔼 This table presents a comparison of the performance of the proposed Swift Sampler (SS) method against several other methods on the CIFAR-10 and CIFAR-100 datasets. It shows the Top-1 accuracy for each method under different levels of added noise (0%, 10%, 20%, 30%, and 40%). The results demonstrate the effectiveness of SS, particularly in the presence of noisy labels.
read the caption
Table 1: SS results on CIFAR10 and CIFAR100 comparisons with other methods. The number pair X / Y means the Top-1 accuracy on CIFAR10 is X% and on CIFAR100 is Y%.

🔼 This table shows the results of an ablation study on the impact of varying the number of optimization steps (Eo) in the Swift Sampler (SS) method on CIFAR-10 dataset with 20% noise. It demonstrates the relationship between the number of optimization steps performed and the resulting Top-1 accuracy. As expected, increasing the number of steps generally leads to higher accuracy, but the gains diminish with additional steps, suggesting a point of diminishing returns.
read the caption
Table 9: Impact of varying the number of optimization steps Eo on the performance of the Swift Sampler (SS) method.

🔼 This table presents the results of the Swift Sampler (SS) method on CIFAR10 and CIFAR100 datasets, compared with other methods (Baseline, REED, MN, LR). It shows the Top-1 and Top-5 accuracy for each method under different noise levels (0%, 0.1, 0.2, 0.3, 0.4). The table demonstrates the effectiveness of SS in achieving higher accuracy, especially in the presence of noisy labels.
read the caption
Table 1: SS results on CIFAR10 and CIFAR100 comparisons with other methods. The number pair X / Y means the Top-1 accuracy on CIFAR10 is X% and on CIFAR100 is Y%.

🔼 This table presents the perplexity scores achieved by the Wiki-GPT model on the Wikitext-2 dataset, both with and without the Swift Sampler (SS). Perplexity is a metric evaluating how well a probability model predicts a sample. Lower perplexity indicates better prediction. The table compares baseline perplexity against results obtained using the SS method on both validation and test sets, demonstrating the method’s effectiveness in improving the model’s predictive performance.
read the caption
Table 11: Comparison of perplexity of Wiki-GPT on Wikitext-2 with and without SS. The number pairs indicate perplexity on the Wikitext-2 validation and test sets respectively.
Full paper#