TL;DR#
Classical optimal control theory relies on simplifying assumptions (linearity, quadratic costs, stochasticity) rarely seen in real-world scenarios. This often leads to algorithms performing poorly on real problems. The paper focuses on solving the challenging bandit non-stochastic control problem, which involves adversarial perturbations, non-quadratic cost functions and bandit feedback mechanisms (i.e. limited information about the system’s response to actions). Existing solutions often suffer from suboptimal regret bounds.
This paper introduces a novel algorithm that significantly improves upon the state-of-the-art. By cleverly reducing the problem to a no-memory bandit convex optimization (BCO) and employing a novel Newton-based update, the authors achieve an optimal Õ(√T) regret bound for strongly convex and smooth cost functions. This algorithm effectively addresses the challenges of high-dimensional gradient estimation and the complexity introduced by memory. The result is a significant contribution to the field, providing a more practical and efficient approach to solving general control problems.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a significant gap in optimal control theory, moving beyond restrictive assumptions like quadratic cost functions and stochastic perturbations. Its results provide new avenues for developing more robust and efficient algorithms for real-world applications. The optimal regret bound achieved is a major step toward solving general control problems. The new algorithm and its analysis are valuable contributions to the field.
Visual Insights#
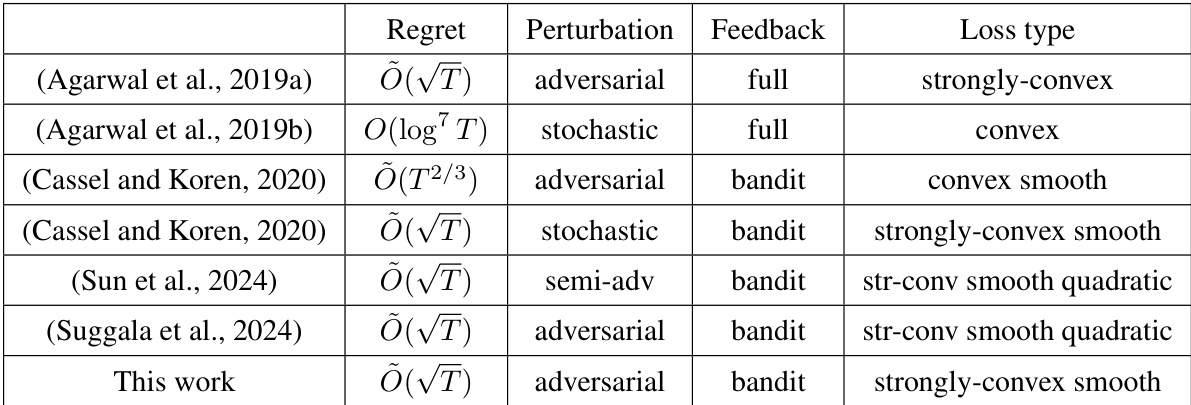
🔼 This table compares the results of this paper with previous works on online non-stochastic control. It shows the achieved regret bound, the type of perturbation (adversarial, stochastic, semi-adversarial), the feedback model (full or bandit), and the type of loss function used (convex, strongly-convex, smooth, quadratic). The table highlights that this paper is the first to achieve an optimal regret bound of Õ(√T) while addressing all three challenges: adversarial perturbations, bandit feedback, and strongly-convex smooth loss functions.
read the caption
Table 1: Comparison of results. This work is the first to address all three generalities with an Õ(√T) optimal regret: (Agarwal et al., 2019a) addressed perturbation + loss, (Cassel and Koren, 2020) addressed feedback + loss, (Suggala et al., 2024) addressed perturbation + feedback. (Cassel and Koren, 2020) also obtained a sub-optimal Õ(T²/³) regret for perturbation + feedback + loss.
Full paper#



















