A Simple yet Scalable Granger Causal Structural Learning Approach for Topological Event Sequences

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it proposes a novel and efficient solution to a critical problem in telecommunication network fault diagnosis. It addresses the scalability and efficiency limitations of existing methods for learning Granger causal graphs from large-scale topological event sequences. This is highly relevant to current research trends focusing on causal inference and network analysis, offering a practical and interpretable approach for real-world applications. The results demonstrate the effectiveness and efficiency of the proposed method, paving the way for further research in causal structure learning and network fault diagnosis.

Visual Insights

#

This figure illustrates the process of generating and inferring Granger causal graphs from topological event sequences in a mobile network. The left panel shows a sample of topological event sequences, where events occur on various devices (nodes) within a network. The right panel depicts the abstraction of this process, including data generation and inference. Solid lines show the event sequence generation process, while dashed lines indicate the process of inferring the causal graph. Observed variables are represented by solid circles and latent variables by dashed circles.

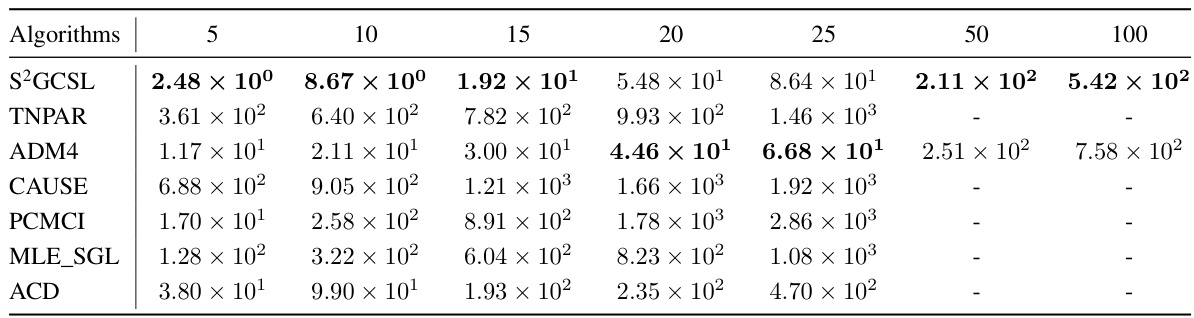
This table presents the wall-clock execution times of several Granger causality algorithms on synthetic datasets of varying sizes. The execution time is reported in seconds, and the algorithms include S²GCSL (the proposed method), TNPAR, ADM4, CAUSE, PCMCI, MLE_SGL, and ACD. The table shows how the execution time scales with the size of the problem, measured by the number of event types (5, 10, 15, 20, 25, 50, and 100). The algorithm with the lowest execution time for each problem size is highlighted in bold. A ‘-’ indicates that an algorithm did not complete execution within one hour.

In-depth insights

#

Scalable Granger Causality

#

Scalable Granger causality tackles a critical challenge in analyzing large-scale datasets, where traditional Granger causality methods fall short due to computational limitations. The core issue is the explosion in the number of pairwise comparisons needed as the dataset grows. Solutions involve leveraging sparse estimation techniques, focusing on identifying only the most significant causal relationships, often employing L1-regularization or similar methods. Another crucial aspect is algorithmic efficiency. Algorithms like those based on gradient descent and efficient optimization routines, or those that exploit the sparsity of the resulting graph, are vital. Distributed computing also plays a large role; decomposing the problem into smaller, manageable chunks and processing them across multiple machines is necessary for larger datasets. Finally, incremental learning methods allow for continuous updates and causal inference without reprocessing the entire dataset every time new data arrives, making the system adaptive and highly efficient. These approaches are essential in domains like network monitoring, finance, and neuroscience, where massive datasets are the norm.

Topological Event Modeling

#

Topological event modeling presents a powerful paradigm for analyzing and understanding complex systems where events are interconnected spatially and temporally. The key innovation lies in integrating topological information, which captures the relationships and structures within the system, into the modeling of events. This approach moves beyond traditional temporal models by explicitly considering the spatial context and network effects. This integration offers significant advantages in prediction accuracy and interpretability. By incorporating network structures, such as proximity or connectivity, models can better capture event propagation patterns, revealing causal relationships and underlying mechanisms. However, challenges remain in effectively handling high-dimensional data and computational complexities inherent in modeling large-scale, intricate systems. Future research directions might include advanced algorithms for efficient inference and model selection to address scalability issues, as well as improved techniques for integrating diverse data types to gain a more holistic understanding of the system’s behavior. Ultimately, topological event modeling opens exciting new avenues for research across various domains demanding a deeper understanding of complex spatiotemporal interactions.

S2GCSL Algorithm

#

The S2GCSL algorithm, designed for Granger causal structural learning on topological event sequences, presents a scalable and efficient solution for the challenging task of root cause identification in large-scale networks. Its core innovation lies in the use of a linear kernel to model activation interactions among event types, offering a computationally efficient approach compared to more complex non-linear methods. The algorithm seamlessly integrates expert knowledge as constraints during optimization, enhancing the interpretability of results. This is particularly beneficial for real-world scenarios where incorporating domain-specific expertise is crucial. Further, it employs gradient descent for efficient optimization of the likelihood function, a significant advantage over gradient-free methods. The combination of these elements suggests a compelling strategy for efficient and interpretable causal analysis in complex, interconnected systems such as telecommunication networks.

Real-World Application

#

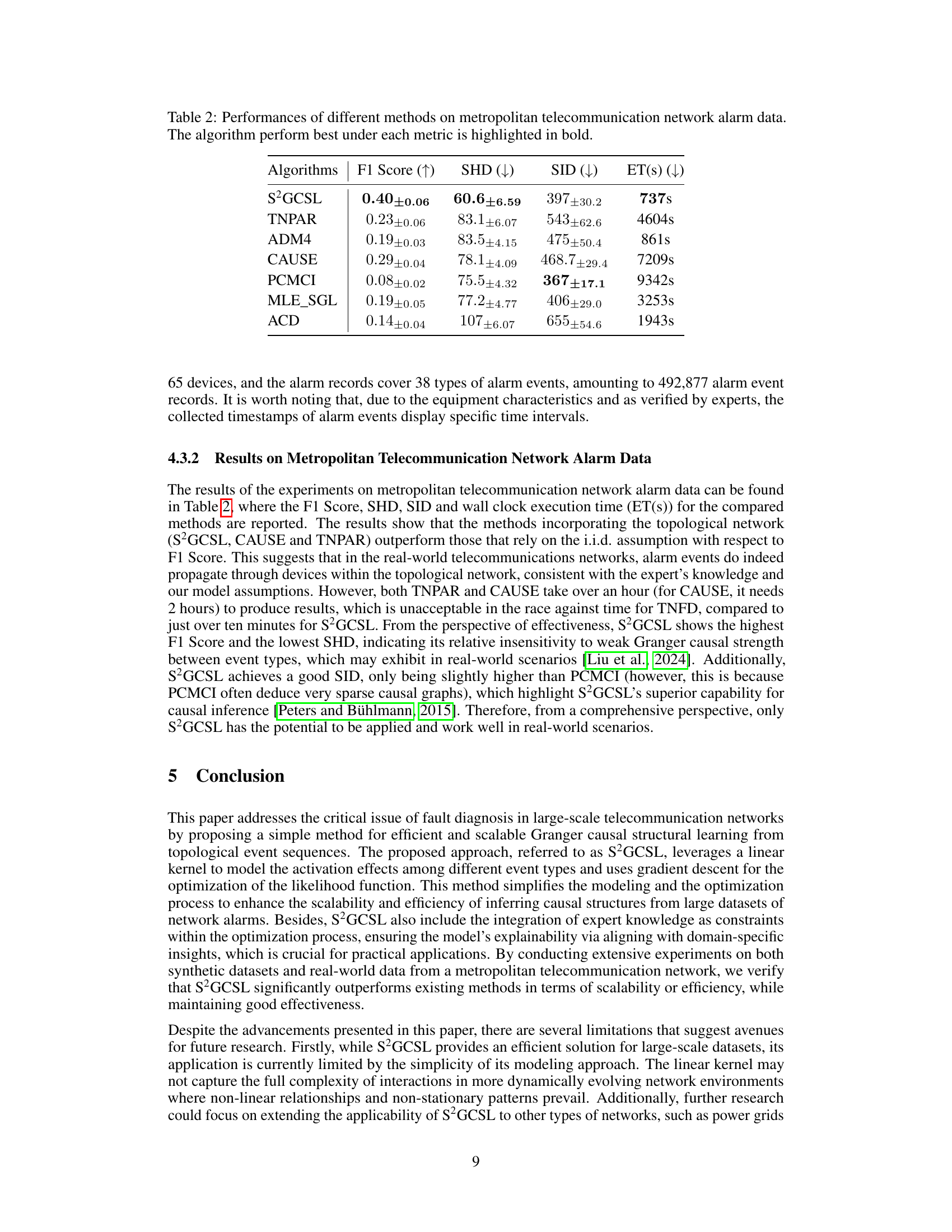
A robust ‘Real-World Application’ section in a research paper would thoroughly demonstrate the practical applicability of the presented method. It should go beyond simply mentioning a real-world dataset; it needs to rigorously evaluate performance against established baselines, using appropriate metrics. A strong section would also address challenges unique to real-world settings, such as data sparsity, noise, and the complexities of real-world constraints. Ideally, it would showcase the method’s scalability and efficiency on a large-scale real-world problem, highlighting its advantages over existing approaches. Detailed analysis of the results, discussing both strengths and limitations, is crucial. The section should conclude with a discussion of the method’s broader impact and potential for future applications, demonstrating its relevance and practical significance.

Future Research

#

Future research directions stemming from this paper could explore several promising avenues. Extending S²GCSL’s applicability to diverse network types, such as power grids or transportation networks, presents a significant challenge, requiring adaptation to handle different event data characteristics and topologies. Investigating more sophisticated activation functions beyond the linear kernel, potentially incorporating neural networks, could enhance the model’s ability to capture complex non-linear relationships among events, thus improving accuracy. A thorough analysis of robustness to noise and missing data within real-world alarm sequences is needed. Finally, developing interpretability techniques to further elucidate the inferred causal relationships will be crucial to facilitating decision-making for engineers. This might involve incorporating techniques from causal discovery or explainable AI. Exploring advanced optimization methods is also key to ensure scalability for extremely large-scale networks.

More visual insights

#

More on figures

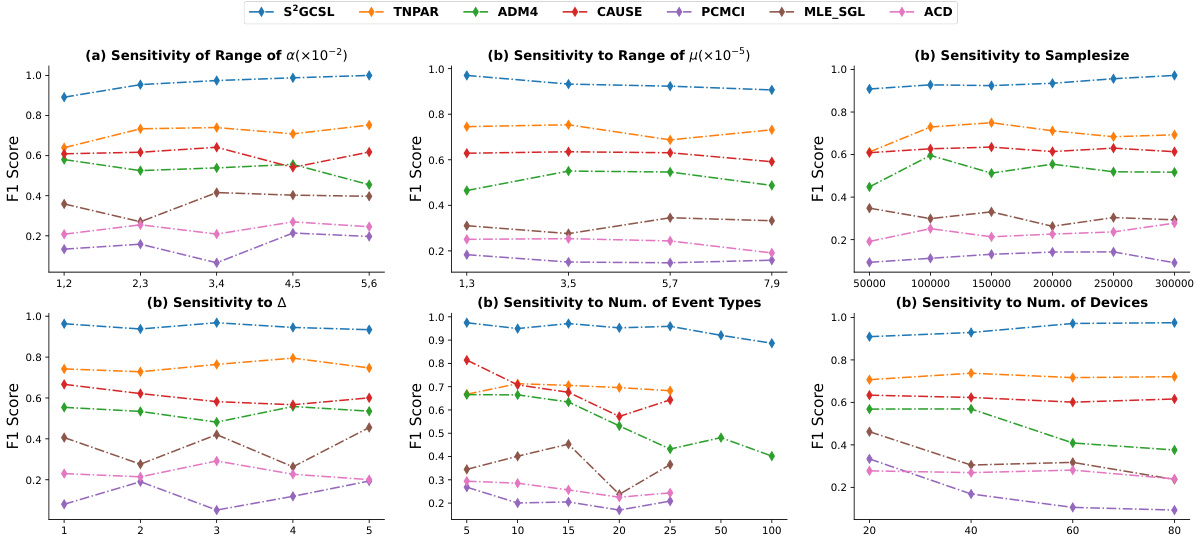
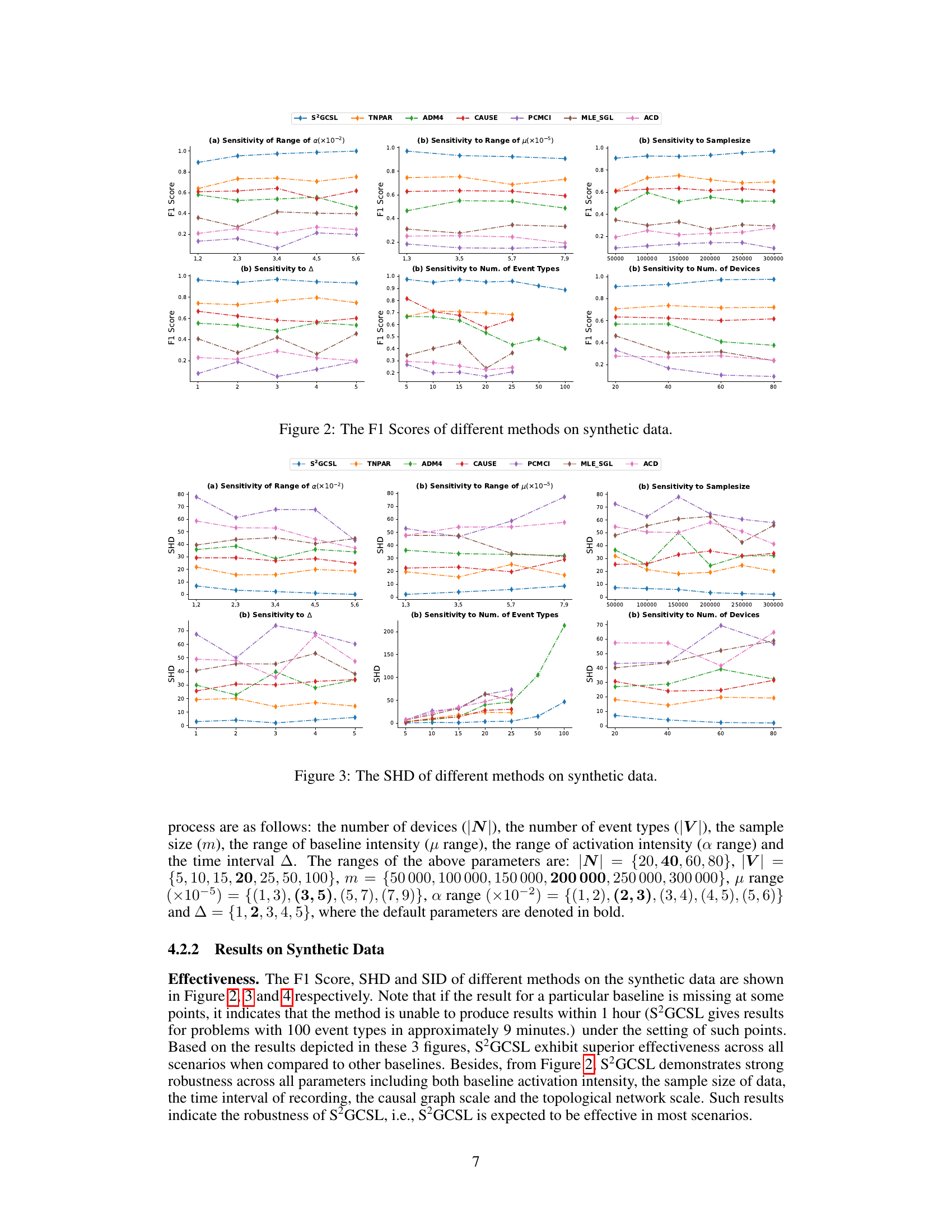
This figure shows the F1 scores achieved by different methods (S²GCSL, TNPAR, ADM4, CAUSE, PCMCI, MLE_SGL, ACD) on synthetic datasets. The F1 score is a metric evaluating the accuracy of a model’s predictions. The figure displays the sensitivity of the F1 score to variations in different parameters of the synthetic data generation process. These parameters include the range of activation intensity (a), the range of baseline intensity (μ), the sample size (m), the time interval (Δ), the number of event types (|V|), and the number of devices (|N|). Each subfigure shows the F1 score across a range of values for one parameter while keeping others constant. This allows assessment of each method’s robustness and effectiveness across various data characteristics.

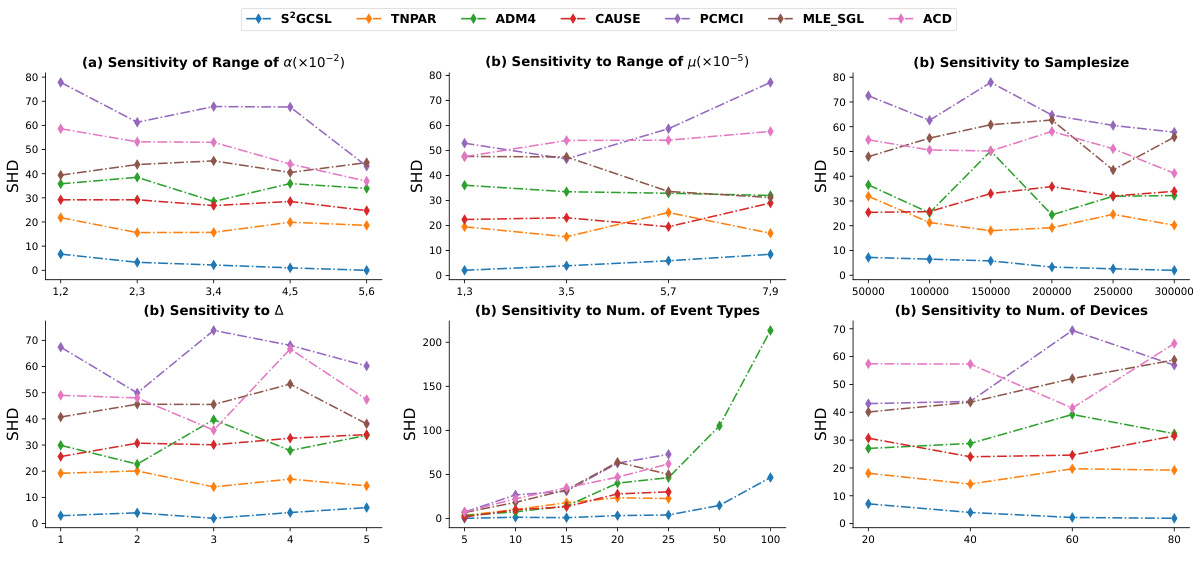
This figure displays the Structural Hamming Distance (SHD) results for various methods on synthetic datasets. The SHD metric measures the difference between two graphs, indicating the number of edge changes (insertions, deletions, or flips) needed to transform one graph into another. Lower SHD values signify better performance. The figure shows how the SHD varies across different parameters of the synthetic data, such as the range of activation intensity, the range of baseline intensity, sample size, time interval, number of event types, and the number of devices. It provides a visual comparison of the different methods’ performance in terms of SHD under varying data characteristics.

The figure shows the Structural Intervention Distance (SID) of different methods on synthetic data. SID measures the similarity between two directed acyclic graphs (DAGs) based on their corresponding causal inference statements, with lower SID indicating greater similarity. The graphs illustrate the sensitivity of the SID for each method (S²GCSL, TNPAR, ADM4, CAUSE, PCMCI, MLE_SGL, ACD) across various parameters of the synthetic data generation process: the range of activation intensity (a), the range of baseline intensity (µ), the sample size, the time interval (Δ), the number of event types (|V|), and the number of devices (|N|). The results show that S²GCSL generally achieves a lower SID across different parameter settings, suggesting its robustness and better performance in causal structure learning compared to other methods.

Full paper

#