TL;DR#
Adversarial robustness in big data is critical for reliability and security against malicious data manipulation. The streaming model, ideal for processing massive datasets, faces challenges in ensuring robustness against adaptive adversaries who can manipulate inputs based on algorithm’s past outputs. Prior work on adversarially robust L_p estimation (calculating a norm of data) in the turnstile streaming model (where data can increase or decrease) faced space limitations due to the dense-sparse trade-off technique. This technique combines sparse recovery and differential privacy, but hasn’t seen improvements since 2022.
This paper introduces improved algorithms for adversarially robust L_p heavy hitters (identifying frequent items) and residual estimation. By leveraging deterministic turnstile heavy-hitter algorithms and a novel method for estimating the frequency moment of the tail vector, the authors achieve better space complexities than previous techniques. The improved algorithms for adversarially robust L_p estimation are a significant step forward, showing that the previously assumed limitations weren’t inherent. The results provide a conceptual advancement, suggesting a new direction for developing more efficient and robust streaming algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial because it directly challenges the prevailing belief that existing dense-sparse tradeoff techniques represent an inherent limitation in adversarially robust streaming algorithms. By presenting improved algorithms and demonstrating their effectiveness, it paves the way for future advancements in this important area of big data processing. The work also offers novel algorithms for heavy hitters and residual estimation, contributing valuable tools for researchers tackling similar challenges.
Visual Insights#
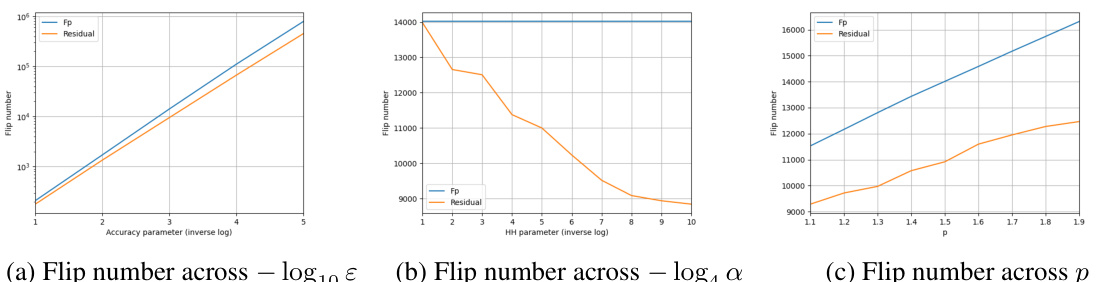
🔼 The figure shows the results of empirical evaluations performed on the CAIDA dataset to compare the flip numbers of the p-th frequency moment and the residual. The results are shown across different accuracy parameters (ε), heavy-hitter parameters (a), and frequency moment parameters (p). Smaller flip numbers suggest that less space is required by the algorithm.
read the caption
Fig. 1: Empirical evaluations on the CAIDA dataset, comparing flip number of the p-th frequency moment and the residual, for ε = a = 0.001 and p = 1.5 when not variable. Smaller flip numbers indicate less space needed by the algorithm.
Full paper#



















