TL;DR#
Multi-agent reinforcement learning (MARL) faces challenges of sample inefficiency and poor generalization, partly due to the lack of structure in typical neural network policies. Existing methods often lack inductive bias, requiring extensive training data. Equivariant Graph Neural Networks (EGNNs), which leverage symmetries in multi-agent scenarios, have shown promise but suffer from an early exploration bias.
This paper introduces Exploration-enhanced Equivariant Graph Neural Networks (E2GN2) to overcome the limitations of EGNNs. E2GN2 introduces a novel method to mitigate the exploration bias while maintaining the equivariance properties of EGNNs. The results show that E2GN2 significantly outperforms standard methods (MLP and GNN) in sample efficiency and generalization across various MARL benchmarks. E2GN2 achieves a 2-5x gain over standard GNNs in generalization tests.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly improves sample efficiency and generalization in multi-agent reinforcement learning (MARL) using a novel approach called Exploration-enhanced Equivariant Graph Neural Networks (E2GN2). This addresses a critical challenge in MARL, paving the way for more reliable and effective solutions in complex multi-agent systems. The findings are relevant to current research trends in geometric deep learning and MARL, and open new avenues for investigation in complex action spaces and biased exploration problems. The improved sample efficiency is particularly impactful, reducing the computational cost and time required to train MARL agents.
Visual Insights#
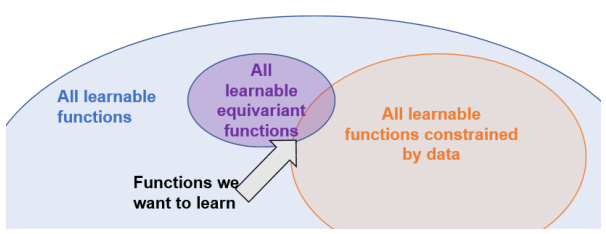
🔼 This figure illustrates how using an equivariant function approximator, which is a function that maintains its properties under certain transformations (like rotations), reduces the search space for learning a target function. The figure shows three overlapping circles representing different sets of functions. The smallest, purple circle represents all learnable equivariant functions. This is a subset of all learnable functions (the larger, light-blue circle). The largest, light-orange circle contains all learnable functions, constrained by the data available during training. The arrow highlights that using equivariance restricts the search to a much smaller set of functions, making the learning process more efficient and likely to find a suitable solution.
read the caption
Figure 1: An example of how using an equivariant function approximator shrinks the total search space.

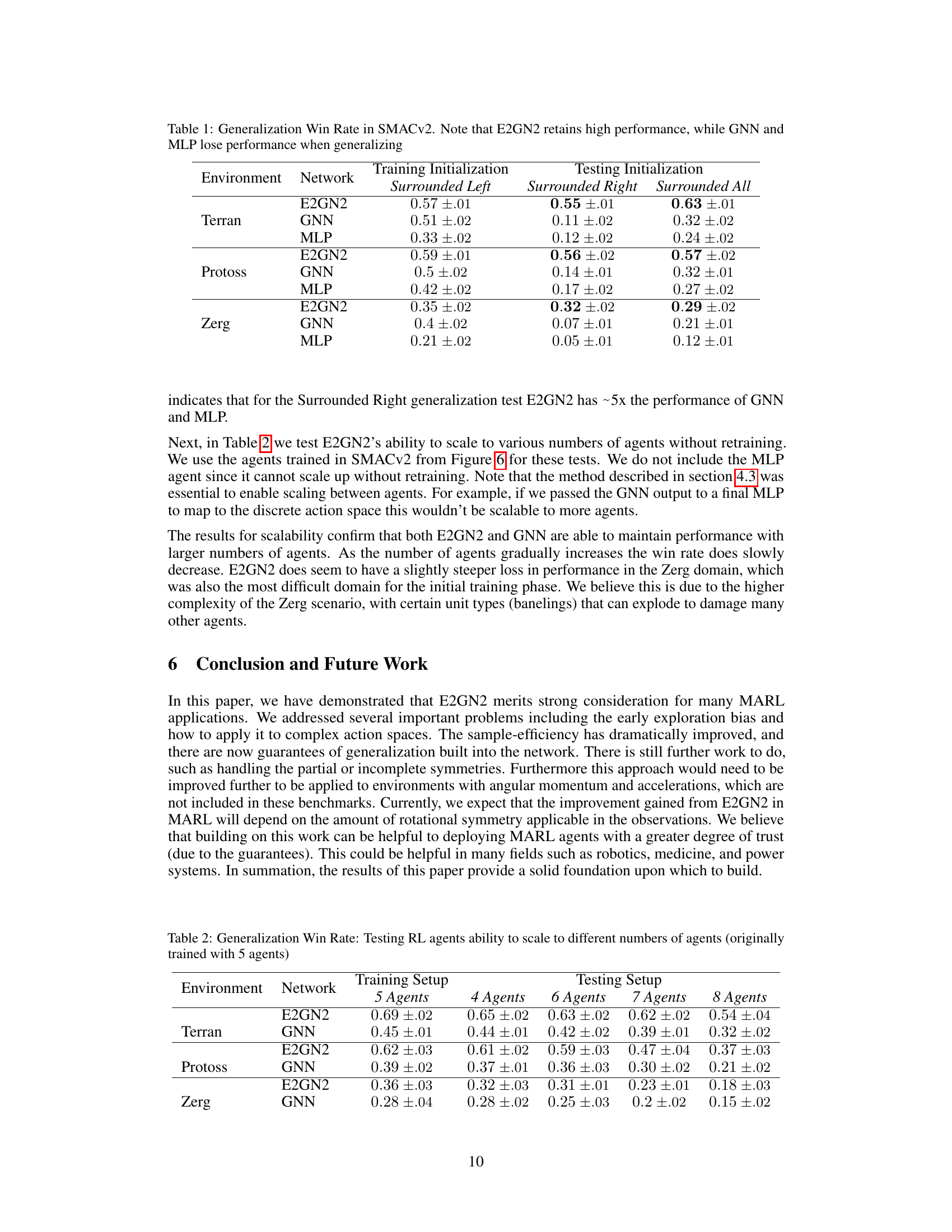
🔼 This table presents the generalization performance of three different neural network architectures (E2GN2, GNN, and MLP) on the StarCraft Multi-Agent Challenge (SMACv2) environment. The agents were trained under a specific map initialization called ‘Surrounded Left’, and then tested on three different initializations: ‘Surrounded Left’ (the same as training), ‘Surrounded Right’ (a mirrored version of the training initialization), and ‘Surrounded All’ (the standard SMACv2 initialization). The table shows the win rate (with standard error) achieved by each model under each testing scenario. The results highlight that E2GN2 maintains consistently high performance across all test conditions, showcasing its strong generalization capabilities, in contrast to GNN and MLP, which exhibit significant performance degradation when tested on different map initializations.
read the caption
Table 1: Generalization Win Rate in SMACv2. Note that E2GN2 retains high performance, while GNN and MLP lose performance when generalizing
In-depth insights#
Equivariant MARL#
Equivariant Multi-Agent Reinforcement Learning (MARL) leverages the inherent symmetries often present in multi-agent environments to improve learning efficiency and generalization. By incorporating equivariant neural networks, such as Equivariant Graph Neural Networks (EGNNs), agents can learn policies that are inherently symmetric with respect to transformations like rotations and reflections. This inductive bias significantly reduces the sample complexity, enabling faster convergence to optimal policies and better generalization to unseen scenarios. A key challenge however, lies in mitigating the exploration bias introduced by the EGNN architecture, which can hinder initial exploration and lead to suboptimal solutions. Exploration-enhanced EGNNs aim to address this bias by modifying the network architecture to promote unbiased exploration from the start. This approach demonstrates improved learning performance across various multi-agent environments, significantly outperforming standard methods like MLPs and GNNs, particularly in tasks with complex action spaces and diverse agent interactions. The ability of equivariant MARL to generalize to unseen scenarios also showcases the practical benefits of exploiting symmetries in the design of MARL algorithms.
E2GN2 Exploration#
The core idea behind E2GN2 exploration is to mitigate the inherent bias in standard Equivariant Graph Neural Networks (EGNNs) that hinders effective exploration, especially in the early stages of multi-agent reinforcement learning (MARL). EGNNs, while powerful for incorporating symmetries, tend to bias agents’ actions towards their current state, limiting exploration of the state-action space. E2GN2 cleverly addresses this by modifying the EGNN architecture. It introduces a mechanism to explicitly decouple the expected value of the output vector from the input vector, thereby ensuring unbiased initial action distributions. This is crucial because unbiased exploration is essential for agents to discover optimal policies and avoid getting stuck in suboptimal regions of the state-action space. The theoretical analysis and empirical results demonstrate E2GN2’s superiority over traditional EGNNs in sample efficiency and generalization, highlighting the significance of addressing exploration bias in MARL for enhanced performance and scalability.
Action Space Adapt#
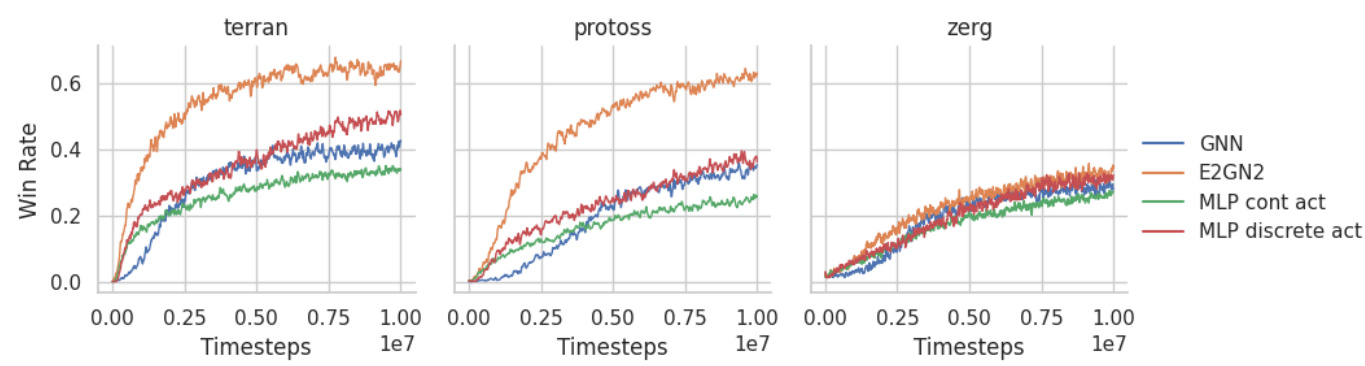
Adapting multi-agent reinforcement learning (MARL) algorithms to handle diverse action spaces is crucial for real-world applications. A thoughtful approach to action space adaptation in MARL should consider the inherent complexities of multi-agent interactions, such as non-stationarity and partial observability. Equivariant Graph Neural Networks (EGNNs) offer a promising avenue, leveraging their inherent symmetry properties to address the challenges posed by complex action spaces. However, naive applications of EGNNs may lead to an exploration bias, hindering performance. Exploration-enhanced EGNNs (E2GN2) can effectively mitigate this bias and provide a more robust solution. This may involve designing flexible architectures capable of handling both discrete and continuous actions simultaneously, potentially incorporating action type selectors or separate processing units for different action components (e.g., movement and targeting). Key considerations include ensuring that the modified architecture maintains the scalability and efficiency benefits of GNNs in the context of multi-agent systems while effectively capturing the equivariance properties of the underlying problem structure. Successful action space adaptation requires careful consideration of how different action types are represented and integrated within the overall architecture, striking a balance between expressiveness, efficiency, and generalization.
Generalization Gains#
A section titled “Generalization Gains” in a research paper would likely explore the model’s ability to perform well on unseen data or tasks. It would delve into the extent to which the model’s learned knowledge transfers to new situations not encountered during training. Key aspects to explore include the model’s robustness to variations in input data, its capacity to adapt to changes in the environment, and how effectively it generalizes across different scenarios. A strong focus would be on comparing performance metrics on both training and test datasets to quantify generalization capabilities and pinpoint areas of strength or weakness. The analysis might also investigate the relationship between model architecture, training methods, and the level of generalization achieved, identifying key factors that contribute to or hinder successful generalization. The results section would likely demonstrate the effectiveness of the proposed approach in improving generalization compared to existing methods, showcasing its advantages in practical applications where adaptability is crucial.
Future Enhancements#
Future enhancements for this research could explore several key areas. Extending E2GN2’s applicability to more complex MARL scenarios with varied agent capabilities and dynamics is crucial. Addressing partial observability, a common challenge in real-world MARL problems, would significantly improve the algorithm’s practicality. Furthermore, investigating the impact of different graph structures and their influence on both efficiency and generalization is warranted. A deeper theoretical analysis could illuminate how equivariance interacts with other inductive biases in learning and exploration, potentially unlocking more powerful MARL architectures. Finally, empirical evaluation on larger-scale and more diverse MARL benchmarks would solidify the findings and demonstrate robustness in complex, real-world settings. Addressing the computational cost of E2GN2, particularly for large-scale problems, is also necessary for wider adoption.
More visual insights#
More on figures

🔼 This figure shows an example of rotational equivariance in the Multi-agent Particle Environment (MPE) simple spread environment. The left panel depicts three agents (red circles numbered 1, 2, and 3) and their optimal actions (red arrows) in a particular configuration. The right panel shows the same agents and their optimal actions after a 90-degree rotation. The key observation is that when the agent positions are rotated, the corresponding optimal actions also rotate accordingly, demonstrating the rotational symmetry inherent in the environment and the importance of equivariance for efficient learning. This symmetry allows an agent to generalize its learned policy from one configuration to another simply by applying the rotation, rather than learning each separately.
read the caption
Figure 2: An example of rotational equivariance/symmetry in MPE simple spread environment. Note as the agent (in red) positions are rotated, the optimal actions (arrows) are also rotated.
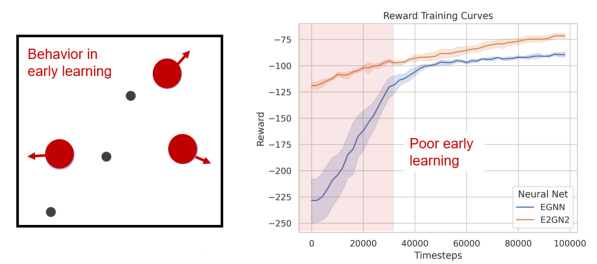
🔼 This figure shows an example of how EGNNs suffer from early exploration bias in the simple spread environment of MPE. The left panel illustrates the agents’ biased movement away from the origin (goal) during the initial training phase, a consequence of the inherent bias in the EGNN structure. The right panel depicts the resulting poor reward performance during this early training period, highlighting the negative impact of the exploration bias on overall learning.
read the caption
Figure 3: An example of biased learning in MPE simple spread environment. Left: We observed the behavior of the EGNN agents in this early training phase. Each agent moved away from the origin due to the EGNN bias. Right: Note the very low reward in early training steps due to the biased policies moving away from the goals.

🔼 This figure shows an example of how an Equivariant Graph Neural Network (EGNN) can be used in multi-agent reinforcement learning (MARL). The input state is structured as a graph where each node represents an agent or entity. Each node has two types of embeddings: an invariant embedding (h) and an equivariant embedding (u). The invariant embeddings are fed into a value head to output a value estimate for the state, while the equivariant embeddings are fed into a policy head to output actions. The figure highlights the way equivariance and invariance are used to generate actions, showing how the output from the EGNN is separated to deal with different properties of the action space.
read the caption
Figure 4: An example of using an Equivariant Graph Neural Network in MARL. Note that the state must be structured as a graph with each node having an equivariant and invariant component. As discussed in 4.3, the output of the policy uses for equivariant (typically spatial) actions, and the for invariant components of the actions
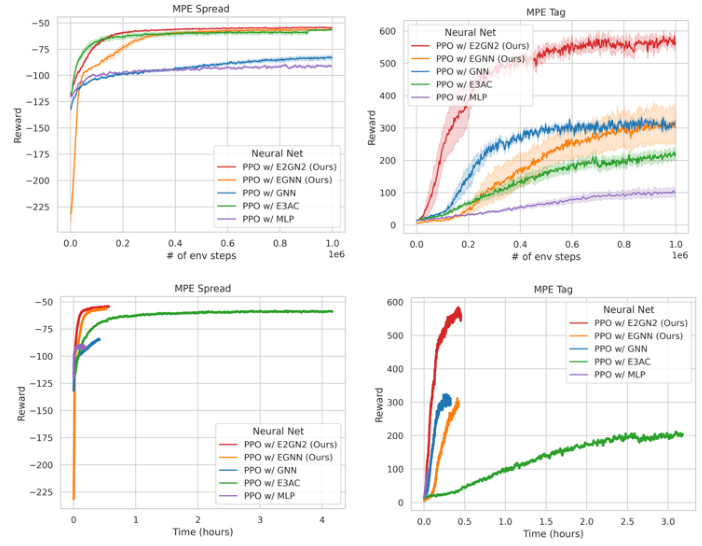
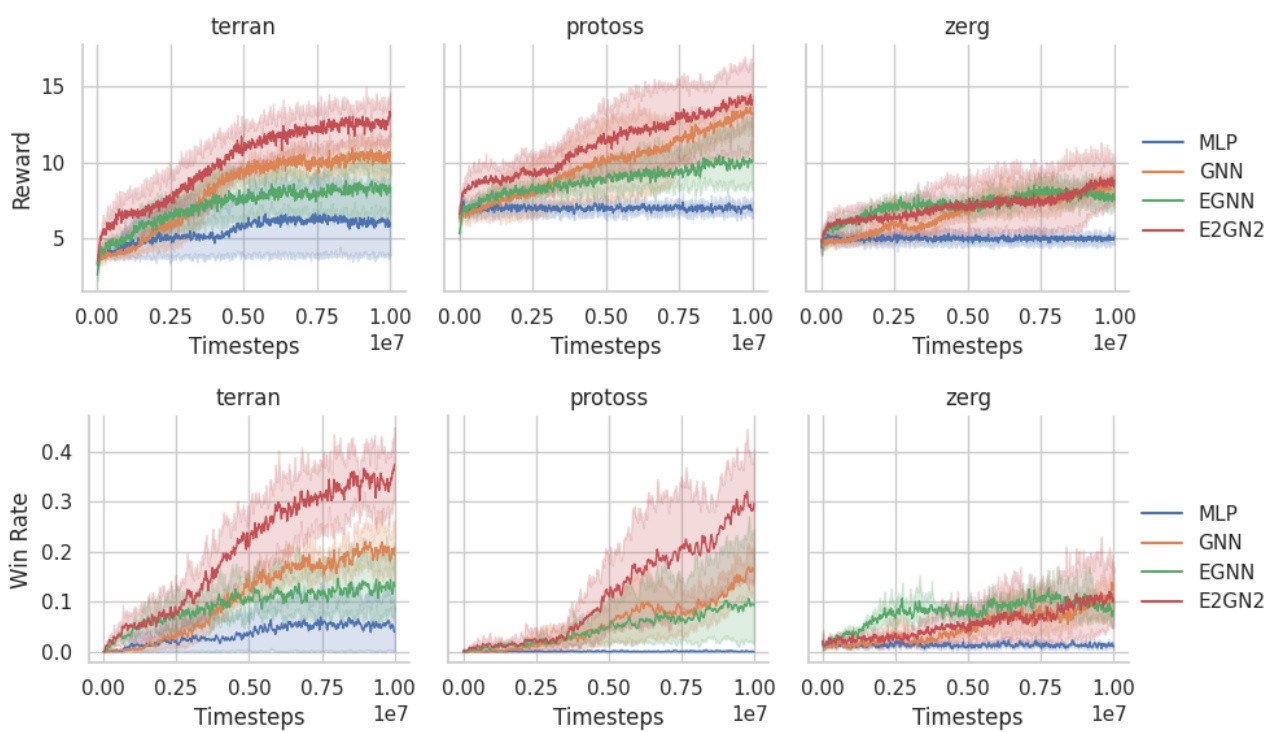
🔼 This figure compares the performance of Proximal Policy Optimization (PPO) using different neural network architectures (MLP, GNN, EGNN, E2GN2, and E3AC) on two Multi-agent Particle Environments (MPE): simple spread and predator-prey (tag). The top row shows reward as a function of environment steps, while the bottom row shows reward as a function of wall-clock time. Standard errors across 10 seeds are shown.
read the caption
Figure 5: Comparing PPO learning performance on MPE with various Neural Networks. (TOP) reward as a function of environment steps. We show the standard errors computed across 10 seeds. (BOTTOM) reward as a function of wall clock time

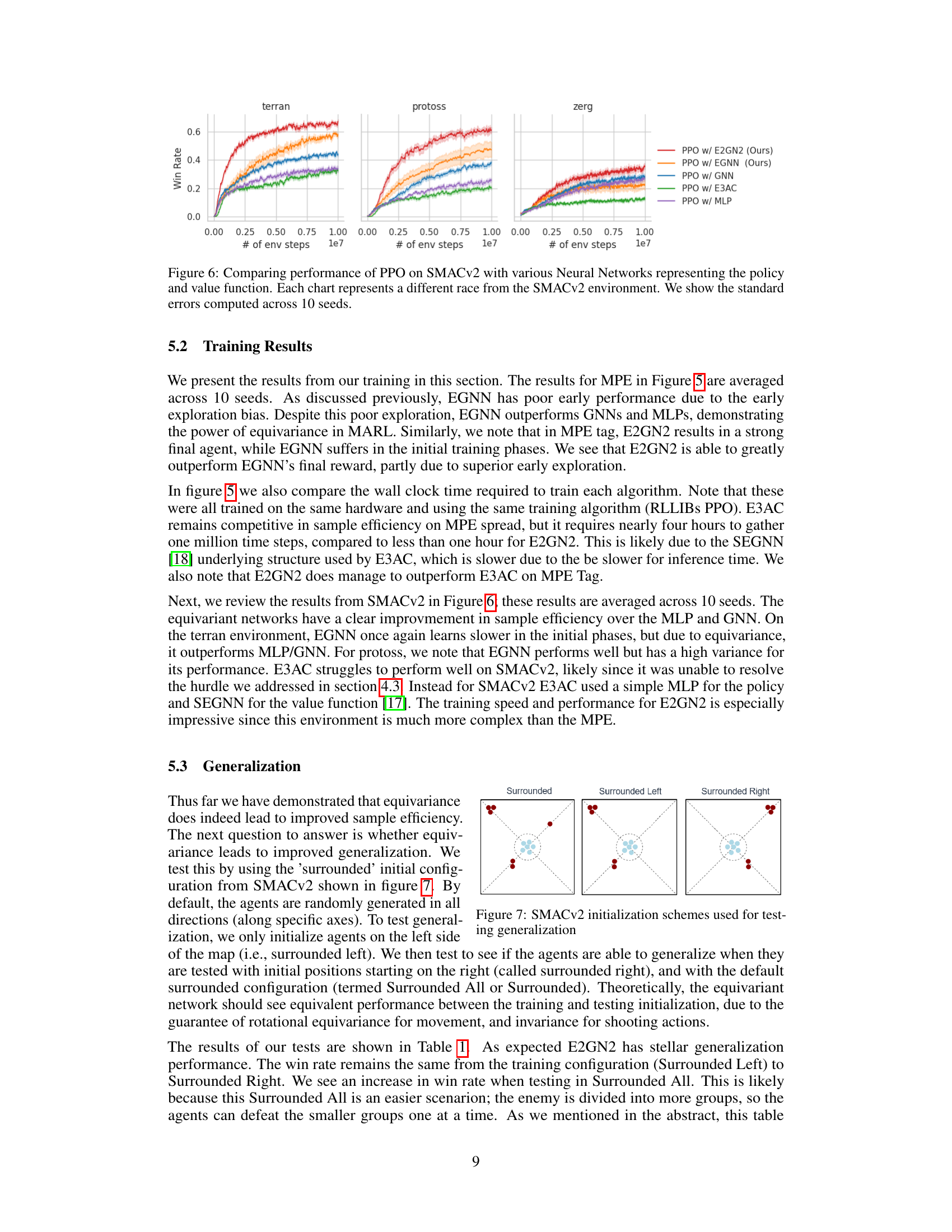
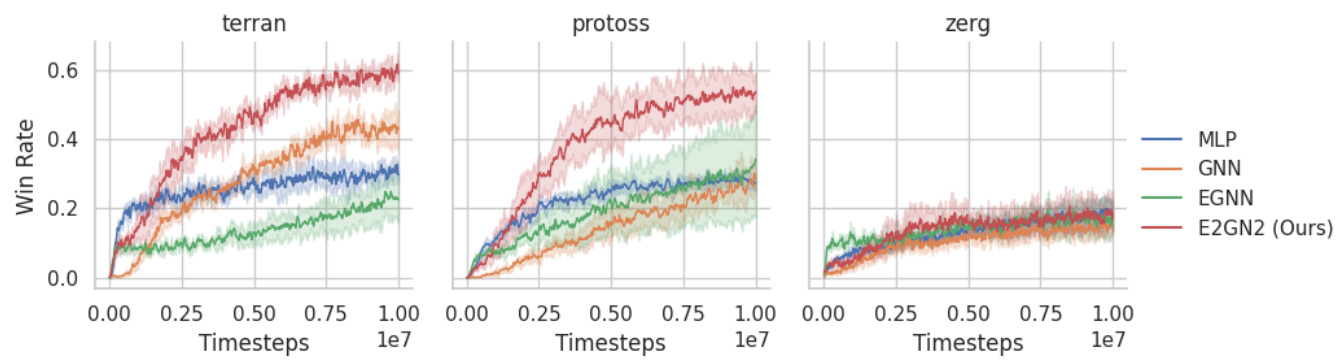
🔼 This figure compares the performance of different neural network architectures (E2GN2, EGNN, GNN, E3AC, and MLP) in the context of Proximal Policy Optimization (PPO) on the Starcraft Multi-Agent Challenge (SMACv2) environment. The performance is measured by win rate and is shown separately for three different races (Terran, Protoss, and Zerg). The standard errors computed across 10 different seeds are displayed to show the variability in performance. This illustrates how the E2GN2 model outperforms other architectures in sample efficiency and achieving a higher win rate in the SMACv2 environment across different races.
read the caption
Figure 6: Comparing performance of PPO on SMACv2 with various Neural Networks representing the policy and value function. Each chart represents a different race from the SMACv2 environment. We show the standard errors computed across 10 seeds.

🔼 This figure shows three different initializations of agents in the StarCraft Multi-Agent Challenge (SMACv2) environment used to test the generalization capabilities of the proposed E2GN2 model. The ‘Surrounded’ configuration shows a symmetric arrangement of agents around the center. The ‘Surrounded Left’ and ‘Surrounded Right’ configurations are variations where agents are placed only on the left or right sides respectively, while maintaining the same overall count and positions relative to the center. These configurations allow the researchers to evaluate whether the learned agent policies generalize to scenarios not seen during training.
read the caption
Figure 7: SMACv2 initialization schemes used for testing generalization
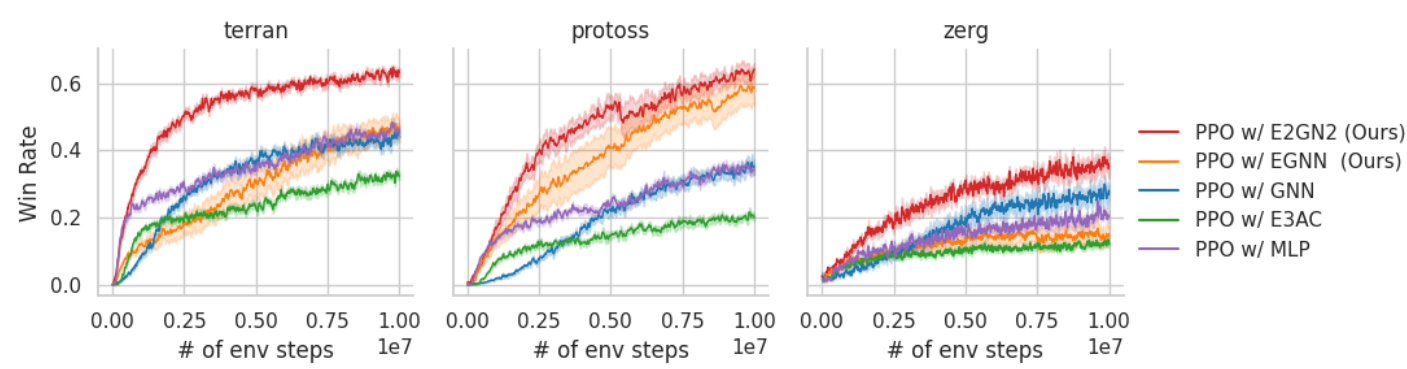
🔼 This figure compares the performance of Proximal Policy Optimization (PPO) using different neural network architectures (E2GN2, EGNN, GNN, E3AC, and MLP) on the StarCraft Multi-Agent Challenge (SMACv2) benchmark. The results are shown for three different races (Terran, Protoss, and Zerg) in SMACv2, illustrating the win rate against the number of environment steps. Error bars represent standard errors calculated across 10 independent training runs. The figure helps visualize the sample efficiency and performance differences between the various neural networks in multi-agent reinforcement learning tasks.
read the caption
Figure 6: Comparing performance of PPO on SMACv2 with various Neural Networks representing the policy and value function. Each chart represents a different race from the SMACv2 environment. We show the standard errors computed across 10 seeds.

🔼 This figure compares the learning performance of Proximal Policy Optimization (PPO) using different neural network architectures (MLP, GNN, EGNN, E2GN2, E3AC) on two Multi-Agent Particle Environment (MPE) tasks: cooperative navigation (spread) and predator-prey (tag). The top panel shows the reward achieved as a function of environment steps, while the bottom panel shows the reward as a function of wall-clock time. Standard errors across 10 random seeds are included for each network in both panels. The results show that E2GN2 consistently outperforms other networks in both reward and training time.
read the caption
Figure 5: Comparing PPO learning performance on MPE with various Neural Networks. (TOP) reward as a function of environment steps. We show the standard errors computed across 10 seeds. (BOTTOM) reward as a function of wall clock time
🔼 This figure compares the performance of Proximal Policy Optimization (PPO) using different neural network architectures (MLP, GNN, EGNN, E2GN2, and E3AC) on two Multi-Agent Particle Environment (MPE) tasks: simple spread and tag. The top panel shows the reward achieved as a function of the number of environment steps, while the bottom panel shows the reward as a function of wall-clock training time. Standard errors across 10 different training runs are included for each method. The results illustrate the differences in sample efficiency and training speed among the different neural networks.
read the caption
Figure 5: Comparing PPO learning performance on MPE with various Neural Networks. (TOP) reward as a function of environment steps. We show the standard errors computed across 10 seeds. (BOTTOM) reward as a function of wall clock time
🔼 This figure compares the learning performance of Proximal Policy Optimization (PPO) using different neural network architectures on two Multi-agent Particle Environment (MPE) tasks: spread and tag. The top panel shows the reward accumulated over environment steps, illustrating the sample efficiency of each approach. The bottom panel displays the reward achieved as a function of wall clock time, highlighting the training speed. The neural networks compared include Multilayer Perceptrons (MLPs), Graph Neural Networks (GNNs), Equivariant Graph Neural Networks (EGNNs), and the proposed Exploration-enhanced Equivariant Graph Neural Networks (E2GN2). Error bars indicate standard errors calculated across 10 independent runs.
read the caption
Figure 5: Comparing PPO learning performance on MPE with various Neural Networks. (TOP) reward as a function of environment steps. We show the standard errors computed across 10 seeds. (BOTTOM) reward as a function of wall clock time
🔼 This figure compares the performance of Proximal Policy Optimization (PPO) with different neural network architectures (MLP, GNN, EGNN, E2GN2, and E3AC) on two Multi-Agent Particle Environment (MPE) tasks: simple spread and tag. The top panel shows the reward achieved as a function of the number of environment steps, while the bottom panel displays the reward as a function of wall-clock training time. Standard errors across 10 different random seeds are shown for each method to demonstrate statistical significance.
read the caption
Figure 5: Comparing PPO learning performance on MPE with various Neural Networks. (TOP) reward as a function of environment steps. We show the standard errors computed across 10 seeds. (BOTTOM) reward as a function of wall clock time
🔼 This figure compares the performance of Proximal Policy Optimization (PPO) using different neural network architectures (MLP, GNN, EGNN, E2GN2, and E3AC) on two Multi-agent Particle Environment (MPE) tasks: simple spread and tag. The top panel shows the cumulative reward over environment steps, illustrating the learning speed and final performance of each method. The bottom panel shows the cumulative reward against wall-clock training time, highlighting the training efficiency. Error bars represent standard errors across 10 independent training runs. The figure demonstrates the improved sample efficiency and final performance of E2GN2, especially in comparison to traditional networks (MLP and GNN) and other equivariant networks (EGNN and E3AC).
read the caption
Figure 5: Comparing PPO learning performance on MPE with various Neural Networks. (TOP) reward as a function of environment steps. We show the standard errors computed across 10 seeds. (BOTTOM) reward as a function of wall clock time
More on tables
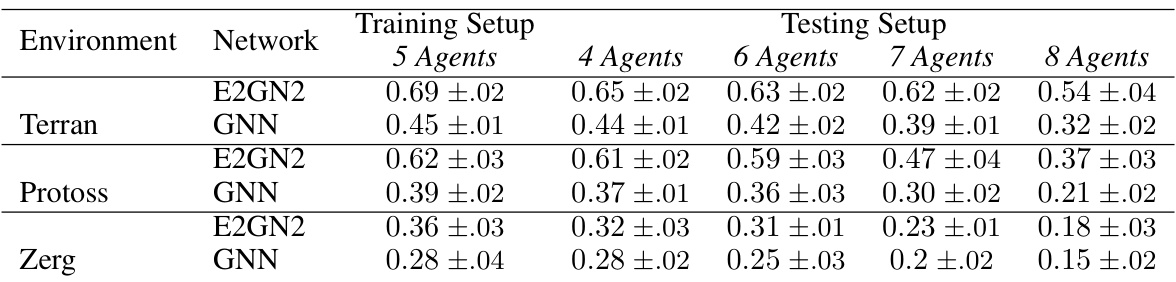
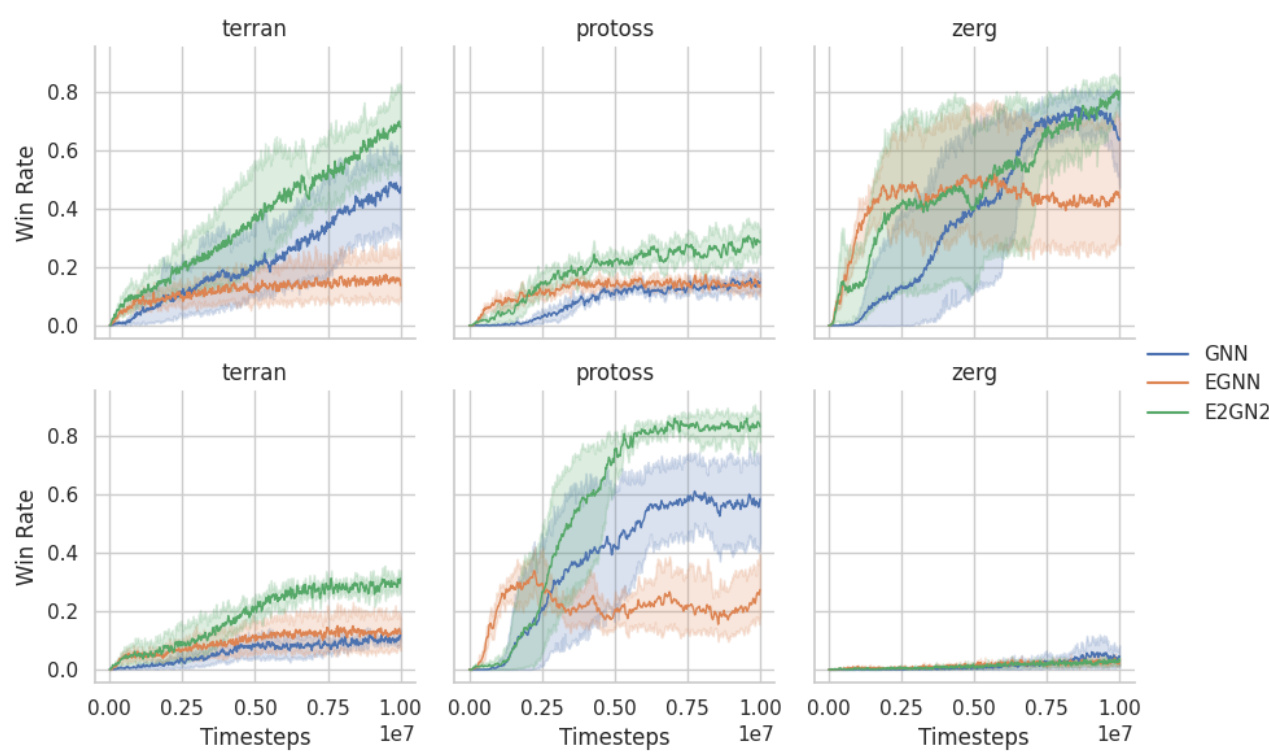
🔼 This table demonstrates the generalization ability and scalability of E2GN2 and GNN models trained on Starcraft Multi-Agent Challenge (SMACv2) with 5 agents. The win rates are tested with different numbers of agents (4, 6, 7, and 8) while keeping the same training configuration, showing the performance consistency across varying numbers of agents. This highlights the scalability and robustness of the models.
read the caption
Table 2: Generalization Win Rate: Testing RL agents ability to scale to different numbers of agents (originally trained with 5 agents)

🔼 This table presents the generalization performance of three different neural network architectures (E2GN2, GNN, and MLP) on the StarCraft Multi-Agent Challenge (SMACv2) environment. The models were trained using a ‘Surrounded Left’ initialization and then tested on three different scenarios: ‘Surrounded Right’, where the agent positions are mirrored horizontally, ‘Surrounded All’, using the standard initialization; and the training scenario itself (‘Surrounded Left’). The win rate, which represents the frequency with which agents achieve victory, is reported for each model under each testing condition. The table highlights the superior generalization performance of E2GN2 compared to GNN and MLP, showing that E2GN2 maintains its performance under various conditions while the others demonstrate a significant drop in performance when tested under different initial conditions.
read the caption
Table 1: Generalization Win Rate in SMACv2. Note that E2GN2 retains high performance, while GNN and MLP lose performance when generalizing

🔼 This table presents the generalization performance of E2GN2, GNN, and MLP models on the StarCraft Multi-Agent Challenge (SMACv2) benchmark. The models were trained using the ‘Surrounded Left’ initialization, where agents are positioned on the left side of the map. Then, their generalization capabilities were evaluated on three different test scenarios: ‘Surrounded Right’ (agents on the right), ‘Surrounded All’ (agents randomly distributed), and the original training configuration. The table displays the win rates achieved by each model in each test scenario, demonstrating E2GN2’s superior generalization ability compared to GNN and MLP, which experience significant performance drops in the test scenarios.
read the caption
Table 1: Generalization Win Rate in SMACv2. Note that E2GN2 retains high performance, while GNN and MLP lose performance when generalizing

🔼 This table presents the generalization performance of three different neural network architectures (E2GN2, GNN, and MLP) on the StarCraft Multi-Agent Challenge (SMACv2) environment. The agents were trained using a specific initial agent configuration (‘Surrounded Left’) and tested on three different configurations: ‘Surrounded Right’, ‘Surrounded All’, and the training configuration. The win rate, a measure of agent success, is reported for each network and testing configuration, across three different unit types (Terran, Protoss, and Zerg). The table highlights that E2GN2 demonstrates significantly better generalization than GNN and MLP, maintaining high win rates across all testing configurations.
read the caption
Table 1: Generalization Win Rate in SMACv2. Note that E2GN2 retains high performance, while GNN and MLP lose performance when generalizing
Full paper#