TL;DR#
Graph convolutional networks (GCNs) are powerful tools for analyzing graph-structured data but suffer from oversmoothing: too many convolutions lead to feature homogenization and reduced classification accuracy. Existing solutions are often ad-hoc or lack rigorous theoretical justification. This necessitates developing more robust techniques that enhance accuracy and prevent performance degradation.
This paper addresses the limitations of vanilla GCNs by rigorously analyzing the performance of graph convolutions with the principal eigenvector removed. The authors use the contextual stochastic block model (CSBM) for theoretical analysis, showing that this modification exponentially improves partial and exact classification accuracy with each additional convolution round. They show that improvements can be achieved up to a saturation point, beyond which performance does not degrade. Furthermore, they extend their analysis to multi-class settings. This work provides strong theoretical guarantees and offers a principled approach to enhance GCNs’ effectiveness.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with graph neural networks (GNNs). It addresses the critical issue of oversmoothing, a significant limitation hindering GNN performance. By providing a rigorous theoretical analysis and proposing a solution, this research opens up new avenues for improving GNN accuracy and efficiency, impacting a wide range of applications relying on graph-structured data.
Visual Insights#

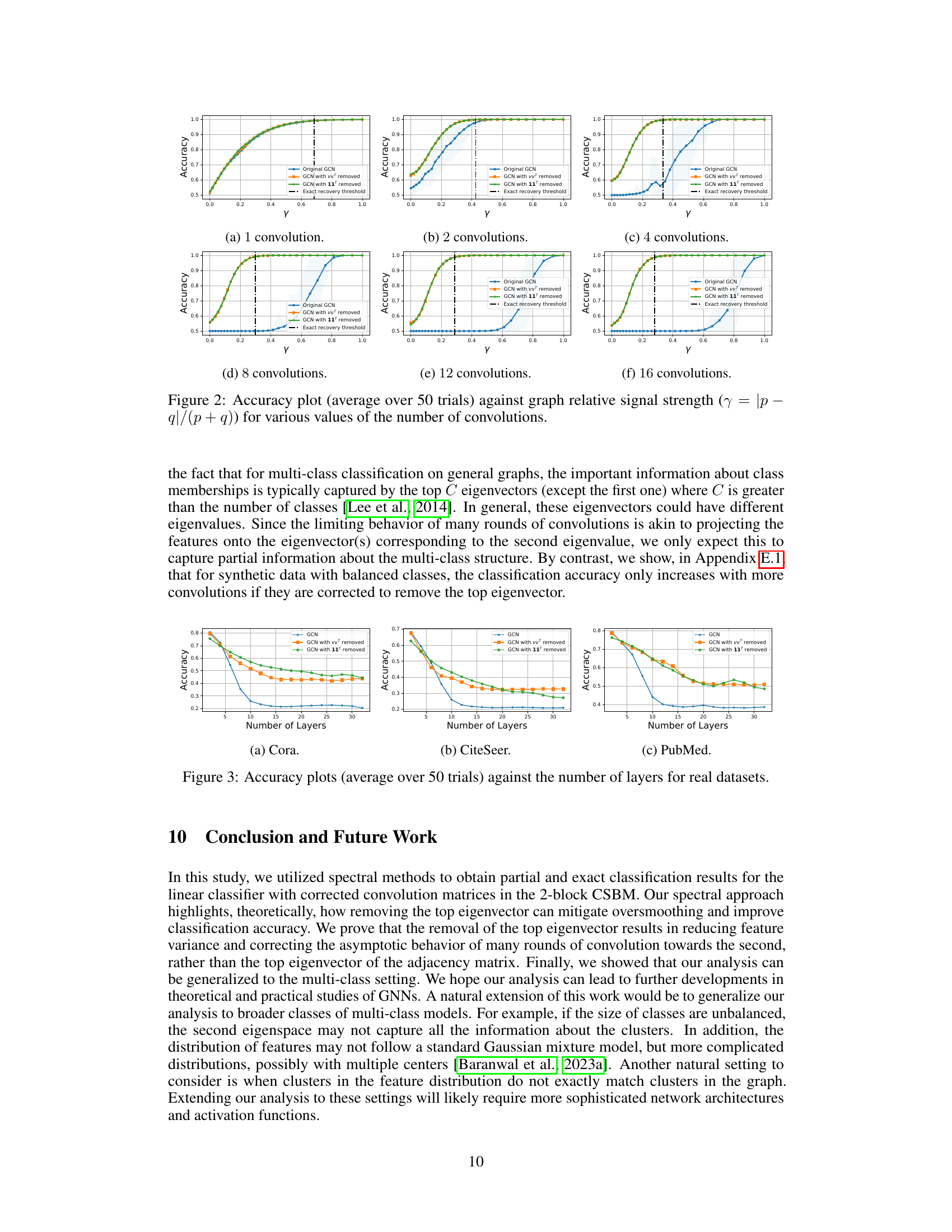
🔼 This figure shows the accuracy of node classification for different numbers of graph convolutions (1, 2, 4, 8, 12, 16) against varying signal-to-noise ratios. Three methods are compared: the original graph convolutional network (GCN), GCN with the principal eigenvector removed from the convolution matrix (using the normalized adjacency matrix), and GCN with the principal eigenvector removed (using the unnormalized adjacency matrix). The results demonstrate the improved performance and robustness of the corrected convolution methods, especially in scenarios with low signal-to-noise ratios, showcasing their ability to mitigate the negative effects of over-smoothing.
read the caption
Figure 1: Accuracy plot (average over 50 trials) against the signal-to-noise ratio of the features (ratio of the distance between the means to the standard deviation) for increasing number of convolutions. Here, v = D1/21 and the “GCN with vυ™ removed” refers to convolution with the corrected, normalized adjacency matrix. “GCN with 11T removed” is the corrected, unnormalized matrix.
In-depth insights#
Corrected Convolutions#
The concept of “Corrected Convolutions” in graph neural networks addresses the oversmoothing problem, where repeated convolutions lead to feature vectors converging towards an uninformative consensus. The core idea is to modify the standard graph convolution operation by removing the principal eigenvector of the adjacency matrix (or a closely related matrix like the normalized Laplacian). This removes the trivial information captured by the all-ones vector, preserving more nuanced information about the graph structure relevant for node classification. The analysis often involves spectral methods, demonstrating that each corrected convolution exponentially reduces the misclassification error until reaching a saturation point, improving the separability threshold. Rigorous theoretical analysis using models like the contextual stochastic block model (CSBM) is used to establish these guarantees. While various normalization techniques exist, the explicit removal of the principal eigenvector offers a direct and interpretable way to combat oversmoothing, especially beneficial for multi-class settings and scenarios with feature variance. The effectiveness of corrected convolutions is further validated empirically with both synthetic and real-world data, showcasing improved performance compared to standard graph convolutions.
Spectral Analysis#
Spectral analysis, in the context of graph neural networks (GNNs) and node classification, is a powerful technique for understanding the behavior of graph convolutions. It leverages the eigenvalues and eigenvectors of matrices representing the graph structure and features to reveal crucial insights into how information propagates and how the model learns. A spectral analysis of the corrected graph convolution matrices allows researchers to rigorously analyze the effects of repeated convolution operations, particularly concerning the issue of oversmoothing. By examining the spectral properties, they can establish bounds on the classification error, quantify the rate of convergence, and identify conditions under which the model achieves exact or near-perfect classification. The analysis of eigenvalues helps determine separability thresholds and saturation levels, revealing limitations and opportunities of the method. Crucially, it helps to quantify the benefit of employing techniques to alleviate oversmoothing, showing how modifications to the graph convolution operation can improve performance. Such insights provide theoretical guarantees on the effectiveness of GNNs, moving beyond purely empirical observations.
CSBM Analysis#
The CSBM (Contextual Stochastic Block Model) analysis section of the paper likely delves into a rigorous theoretical examination of graph convolutional neural networks (GCNNs). It probably leverages the CSBM framework to model graph structure and node features, enabling a precise mathematical analysis of GCNN performance. Key aspects likely include examining the impact of multiple convolutions, potentially highlighting the oversmoothing phenomenon. The analysis would likely focus on partial and exact classification accuracy, possibly providing bounds or thresholds for successful classification based on the CSBM’s parameters (e.g., edge probabilities, feature distribution). A spectral analysis would be essential, potentially using techniques to analyze eigenvalues and eigenvectors of graph matrices after applying graph convolution operations. Key theoretical guarantees on classification error reduction with each round of convolutions are likely presented, potentially showcasing conditions under which the error converges exponentially or reaches saturation. The multi-class setting is likely also explored, extending the analysis beyond binary classifications. Overall, this section likely serves to bridge empirical observations with rigorous theoretical underpinnings, providing valuable insights into the inner workings of GCNNs and their performance limitations, especially regarding oversmoothing.
Over-smoothing Fix#
The phenomenon of over-smoothing in graph neural networks (GNNs) severely limits their performance on graph data with many layers. A common over-smoothing fix involves modifying the graph convolutional operation to mitigate the issue. This could be achieved by using a corrected matrix that removes the principal eigenvector from the graph convolution matrix, thereby preventing the features from collapsing to a single value. This technique prevents the information from vanishing as the number of layers increases, thereby significantly improving the classification accuracy. Spectral analysis plays a crucial role in this type of fix, allowing for a theoretical understanding of how the corrected convolution improves classification by bounding the mean-squared error between the true signal and convolved features, and ultimately proves linear separability. While the effectiveness of over-smoothing fixes varies depending on the underlying graph structure and the choice of correction method, this approach of targeted manipulation of the convolution matrix is a promising direction. Empirical studies in real-world datasets confirm these theoretical results, indicating the practical applicability and effectiveness of this approach.
Future Directions#
Future research could explore extending the theoretical analysis to more complex graph structures and realistic data distributions beyond the two-class and multi-class CSBM. Investigating the impact of different feature distributions and the presence of noise on the performance of corrected graph convolutions would provide valuable insights. Furthermore, exploring the applicability of these techniques to various graph learning tasks, such as link prediction, graph generation, and node embedding, is warranted. A key area for investigation is the effect of network topology on the effectiveness of corrected convolutions, potentially necessitating adjustments or alternative correction strategies depending on graph properties. Finally, empirical studies on large-scale real-world datasets are crucial to validate the theoretical findings and assess the practical implications of corrected graph convolutions for different application domains.
More visual insights#
More on figures

🔼 The figure shows the accuracy of different graph convolutional networks (GCNs) against the signal-to-noise ratio of node features for various numbers of convolutions. Three types of GCNs are compared: the original GCN, a GCN with the principal eigenvector removed (GCN with vvT removed), and a GCN with the all-ones vector removed (GCN with 11T removed). The results demonstrate that removing the principal or all-ones eigenvector improves the performance of GCNs, especially in low signal-to-noise settings.
read the caption
Figure 1: Accuracy plot (average over 50 trials) against the signal-to-noise ratio of the features (ratio of the distance between the means to the standard deviation) for increasing number of convolutions. Here, v = D1/21 and the “GCN with vυ™ removed” refers to convolution with the corrected, normalized adjacency matrix. “GCN with 11T removed” is the corrected, unnormalized matrix.

🔼 This figure compares the performance of the original GCN and corrected graph convolution on three real-world citation network datasets: Cora, Citeseer, and PubMed. The x-axis represents the number of layers in the graph convolutional network, and the y-axis represents the accuracy of node classification. The figure shows that the accuracy of the standard GCN decreases significantly as the number of layers increases (oversmoothing). In contrast, the accuracy of the corrected graph convolution remains relatively stable or even improves slightly. This demonstrates the effectiveness of the proposed method in mitigating the oversmoothing problem in real-world graph data.
read the caption
Figure 3: Accuracy plots (average over 50 trials) against the number of layers for real datasets.

🔼 The figure shows accuracy plots for different numbers of graph convolutions, comparing the original GCN model against two corrected versions. The x-axis represents the signal-to-noise ratio, and the y-axis shows the accuracy. The plots demonstrate that the corrected graph convolution methods maintain accuracy even with noisy data, unlike the original GCN which shows a performance drop with more convolutions.
read the caption
Figure 1: Accuracy plot (average over 50 trials) against the signal-to-noise ratio of the features (ratio of the distance between the means to the standard deviation) for increasing number of convolutions. Here, v = D1/21 and the “GCN with vυ™ removed” refers to convolution with the corrected, normalized adjacency matrix. “GCN with 11T removed” is the corrected, unnormalized matrix.

🔼 The figure shows the accuracy of node classification for different numbers of graph convolutions with and without the principal eigenvector removed from the adjacency matrix. The x-axis represents the signal-to-noise ratio (SNR) of node features, and the y-axis shows the accuracy of a linear classifier trained on the graph convolution output. Three variations are compared: a standard Graph Convolutional Network (GCN), a GCN with the top eigenvector (vvT) removed, and a GCN with the all-ones vector (11T) removed. The plots demonstrate how removing the top eigenvector improves accuracy, particularly at lower SNRs and for higher numbers of graph convolutions. The plots visualize the effectiveness of corrected graph convolutions in mitigating oversmoothing.
read the caption
Figure 1: Accuracy plot (average over 50 trials) against the signal-to-noise ratio of the features (ratio of the distance between the means to the standard deviation) for increasing number of convolutions. Here, v = D1/21 and the “GCN with vυ™ removed” refers to convolution with the corrected, normalized adjacency matrix. “GCN with 11T removed” is the corrected, unnormalized matrix.

🔼 The figure compares the performance of three graph convolutional network models (GCN, GCN with the principal eigenvector removed, and GCN with the all-ones vector removed) on three real-world citation networks (Cora, CiteSeer, and Pubmed). The x-axis represents the number of layers in the GCN, and the y-axis represents the classification accuracy. The plot shows that the accuracy of the standard GCN decreases as the number of layers increases, exhibiting oversmoothing. In contrast, the accuracy of the corrected GCNs remains stable or even slightly improves as the number of layers increases, demonstrating the effectiveness of removing the principal eigenvector in mitigating oversmoothing.
read the caption
Figure 3: Accuracy plots (average over 50 trials) against the number of layers for real datasets.
Full paper#