MGF: Mixed Gaussian Flow for Diverse Trajectory Prediction

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it addresses the critical issue of diversity in trajectory prediction, a limitation of current methods. By proposing MGF, it offers a novel approach with improved diversity and controllability of predicted trajectories, opening new avenues for research in this active field. Its invertible nature allows for a better understanding of probability, impacting downstream tasks.

Visual Insights

#

This figure compares three different generative models for trajectory prediction. (a) shows a non-invertible model which cannot estimate probability density. (b) shows a flow-based model that uses a standard Gaussian prior, which limits diversity and controllability. (c) shows the proposed Mixed Gaussian Flow (MGF), which uses a mixed Gaussian prior to improve diversity and controllability.

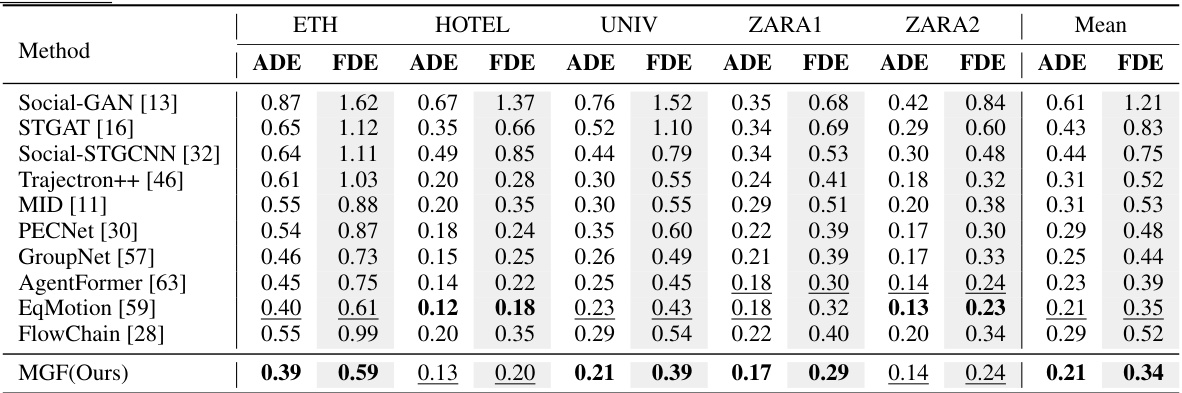
This table presents the performance comparison of various trajectory prediction methods on the ETH/UCY dataset using the ‘best-of-20’ evaluation metric. Lower scores indicate better performance. The table shows ADE (Average Displacement Error) and FDE (Final Displacement Error) for each method across five different subsets of the dataset (ETH, HOTEL, UNIV, ZARA1, ZARA2) and also provides the average performance across all subsets.

In-depth insights

#

Diverse Trajectory Prediction

#

Diverse trajectory prediction is a crucial problem in robotics and autonomous driving. The challenge lies in accurately predicting not just one likely future trajectory, but a range of plausible paths. This is important because agents, such as pedestrians or vehicles, may exhibit diverse behaviors due to uncertain intentions or unexpected events. Existing methods often struggle to generate sufficient diversity, leading to unrealistic and brittle predictions. A key issue is the mismatch between the typically unimodal nature of standard generative models and the often multimodal, asymmetric nature of real-world trajectory distributions. Addressing this requires innovative approaches to model representation, such as using richer priors than simple Gaussians. This includes representing agent movement with a mixed Gaussian model, capturing diverse movement patterns more effectively and leading to better diversity in predictions. Invertibility in generative models is also highly desirable as this allows likelihood estimation for each trajectory hypothesis, useful for downstream decision-making. Finally, methods for evaluating diversity are crucial, moving beyond simple metrics that focus on accuracy rather than the spectrum of possible future outcomes.

Mixed Gaussian Flow

#

The proposed “Mixed Gaussian Flow” model cleverly addresses the limitations of standard Gaussian priors in trajectory prediction. By replacing the single-modal standard Gaussian prior with a data-driven mixture of Gaussians, MGF significantly enhances the model’s capacity to capture the multi-modal and asymmetric nature of real-world trajectory distributions. This improvement in representation directly translates to increased diversity in generated trajectories, a critical aspect often lacking in existing generative models. The invertibility of the normalizing flow framework ensures the model maintains controllability and allows for likelihood estimation of generated trajectories, thus adding further value to its practical applications. The construction of the mixed Gaussian prior involves data-driven clustering to identify representative trajectory patterns in the training set, thus making the method highly adaptable to various trajectory datasets. This intelligent integration of statistical learning and flow-based generative models yields a powerful and versatile tool for probabilistic trajectory prediction, boasting both superior diversity and refined controllability.

MGF: Diversity Metrics

#

The heading ‘MGF: Diversity Metrics’ suggests a focus on evaluating the diversity of trajectories generated by the Mixed Gaussian Flow (MGF) model. Standard trajectory prediction metrics like Average Displacement Error (ADE) and Final Displacement Error (FDE) primarily assess the accuracy of a single predicted trajectory. MGF likely introduces new metrics to capture the spread and variety of generated trajectories, acknowledging that diverse, plausible outcomes are crucial for realistic trajectory prediction. These metrics would likely quantify the diversity within a set of predicted trajectories from the MGF model, rather than focusing on individual trajectory accuracy. The development of these metrics addresses a limitation of existing trajectory prediction methods, which often struggle to generate sufficiently diverse predictions. This is because they typically use a single-modal Gaussian distribution for their prior, failing to capture the inherent multi-modality and asymmetry of real-world trajectories. By directly addressing the diversity of predictions, the paper demonstrates a more comprehensive evaluation of the model’s capability in handling uncertainty inherent in predicting future human movement.

Ablation Study: MGF

#

An ablation study on the Mixed Gaussian Flow (MGF) model would systematically evaluate the contribution of its core components. Removing the mixed Gaussian prior and reverting to a standard Gaussian would assess its impact on both trajectory alignment and diversity, likely showing reduced diversity and potentially improved alignment. Eliminating prediction clustering would reveal whether this post-processing step improves diversity at the expense of alignment accuracy. The effect of using a learnable variance versus a fixed variance would demonstrate the importance of adaptive variance modeling for capturing diverse trajectory patterns, while removing the inverse loss would highlight its importance in balancing alignment and diversity. By systematically isolating these components, the ablation study would precisely quantify their impact on MGF’s performance, offering valuable insights into the model’s design choices and informing future improvements.

MGF Limitations

#

The Mixed Gaussian Flow (MGF) model, while demonstrating improvements in trajectory prediction diversity and controllability, is not without limitations. Computational constraints are a significant factor, as the model’s complexity increases with the number of Gaussian components in the prior. This could hinder scalability to extremely large datasets or high-dimensional trajectory representations. Data dependency is another concern; the effectiveness of MGF hinges on the quality and representativeness of the training data. The reliance on a specific data preprocessing technique can introduce bias or limit generalizability. Furthermore, the model’s performance could be impacted by the choice of hyperparameters, particularly those related to the Gaussian Mixture Model and the normalizing flow architecture. Finally, the evaluation focuses on visible pedestrian movement. The lack of consideration for occlusions, interactions with dynamic elements (e.g., vehicles), or unpredictable agent behavior could limit the model’s accuracy and robustness in complex real-world scenarios.

More visual insights

#

More on figures

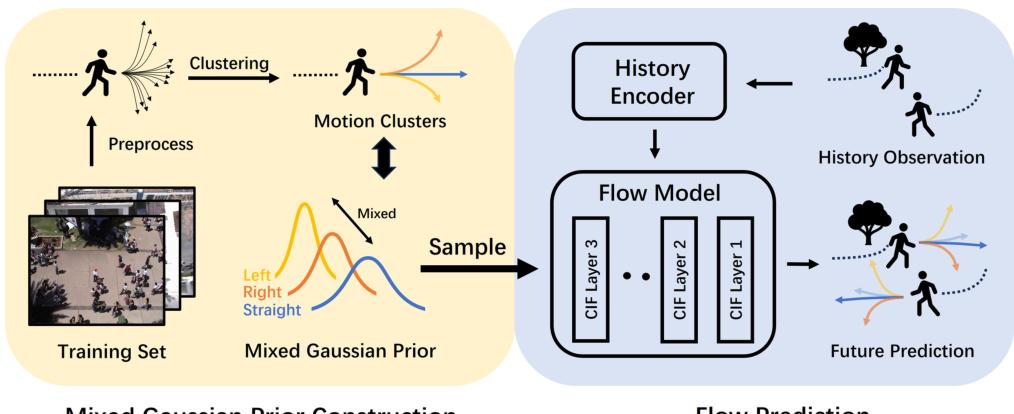
This figure illustrates the Mixed Gaussian Flow (MGF) model. The left side shows the process of constructing the mixed Gaussian prior. The training data is preprocessed, clustered into groups representing different motion patterns, and used to fit a mixture of Gaussian distributions, creating a multi-modal prior that reflects the diversity of movements in the training data. The right side shows the flow prediction process, where the history encoder takes historical trajectory observations as input. This information is used, along with a sample from the mixed Gaussian prior, by the flow model (a series of CIF layers). This model transforms the sample into a prediction of future trajectories. The model architecture enables both diversity of predictions (from the mixed Gaussian prior) and controllability (due to the prior’s parametric nature and invertible inference).

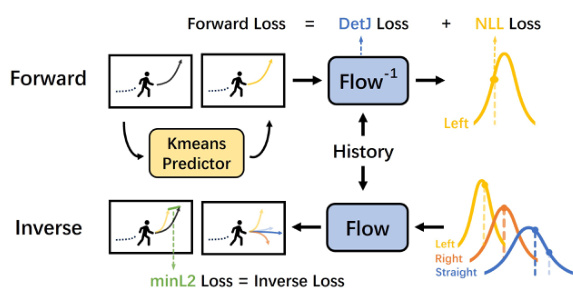
This figure illustrates the Mixed Gaussian Flow (MGF) model architecture. During training, the model learns a mixed Gaussian prior distribution from the training data by clustering trajectory patterns. This prior represents the diverse movement patterns of agents. During inference, samples are drawn from this mixed Gaussian prior, and then passed through a normalizing flow model. The normalizing flow model maps the samples from the simple mixed Gaussian prior to the complex distribution of possible future trajectories. The invertibility of the normalizing flow allows for probability density estimation, making the model more controllable. The model incorporates history information through an encoder. The overall design allows for diverse and controllable trajectory generation, improving the quality of probabilistic trajectory prediction.

This figure demonstrates the diversity of trajectory predictions generated by the Mixed Gaussian Flow (MGF) model on the ETH dataset. Each set of predictions originates from a specific past trajectory (black dotted line) and its corresponding ground truth future trajectory (black solid line with stars). The various colored lines represent the different predicted trajectories generated by MGF. The color of a prediction corresponds to the cluster in the mixed Gaussian prior from which its initial noise sample was drawn. The figure visually shows that MGF produces diverse predictions based on the clusters within the mixed Gaussian prior, covering various possible future trajectories.

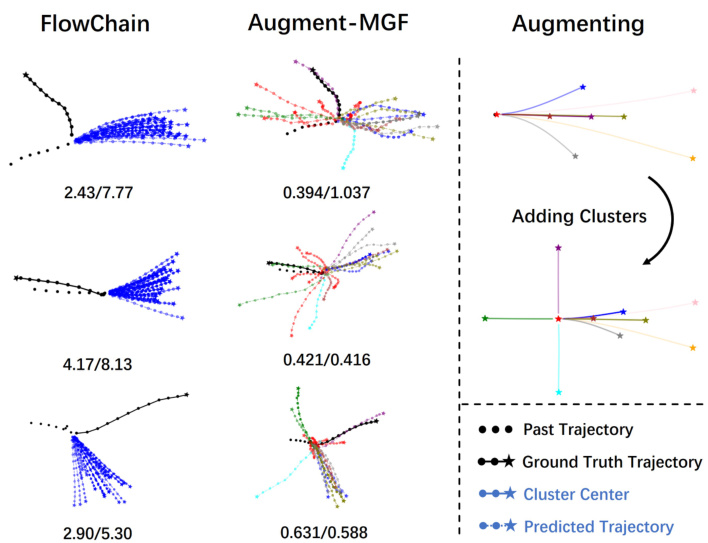
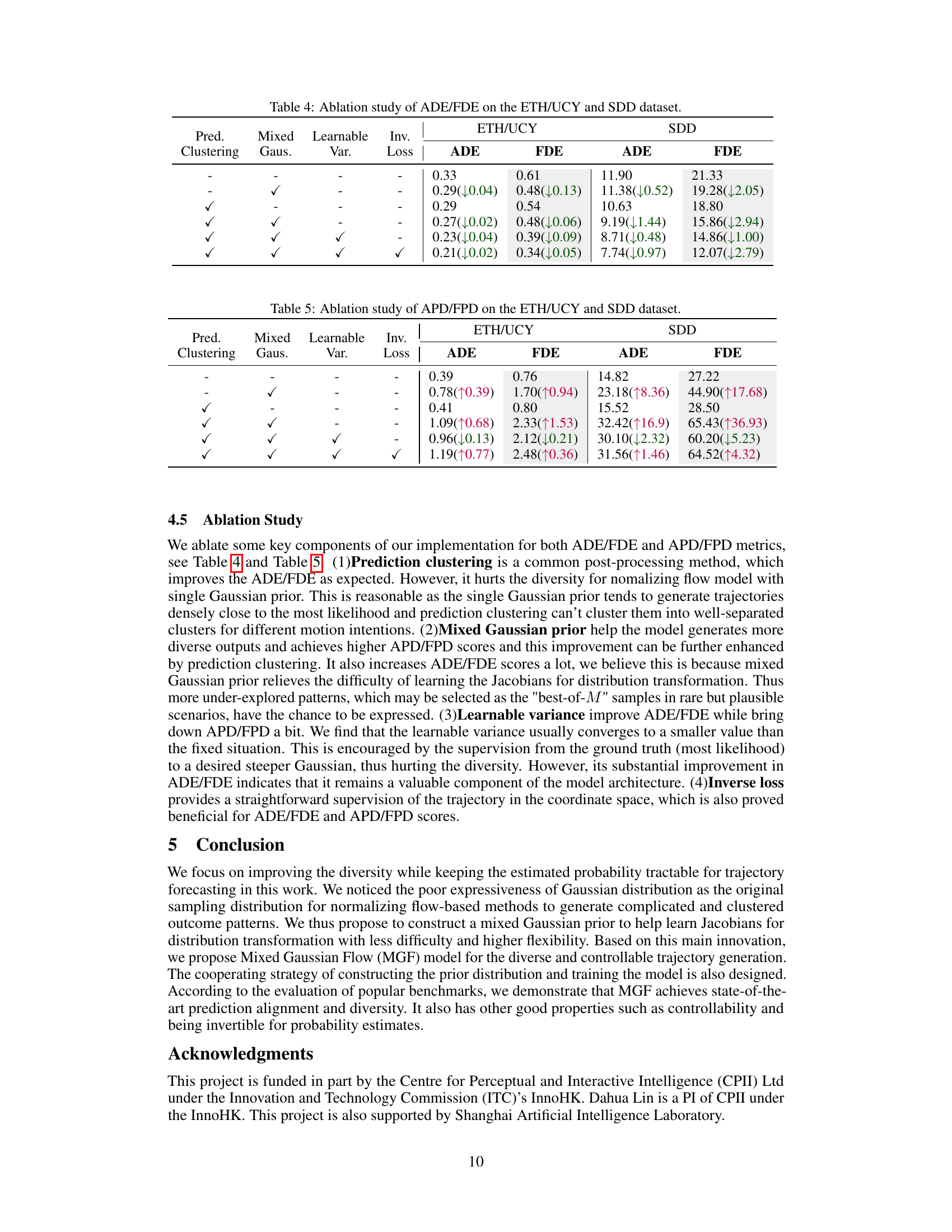
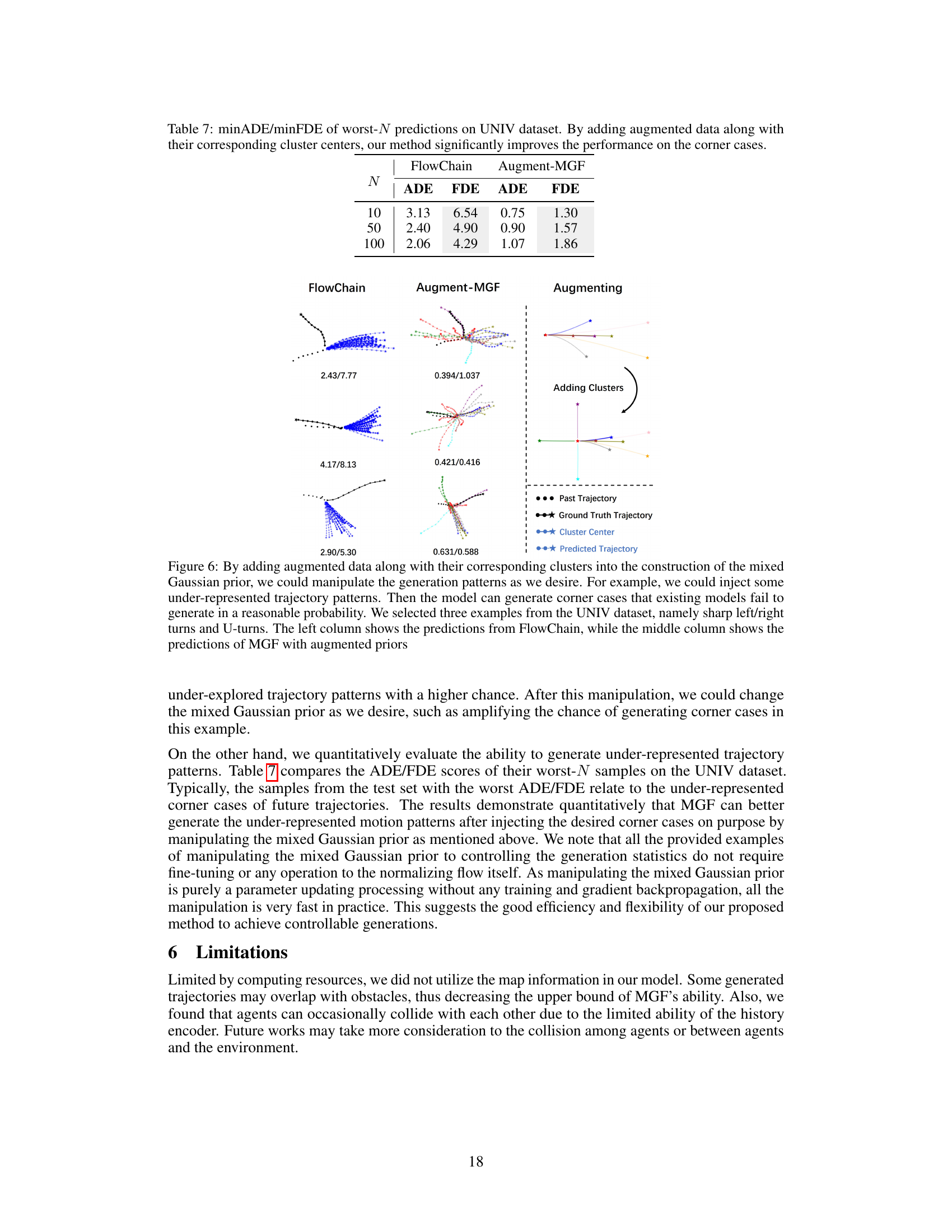
This figure demonstrates how data augmentation affects trajectory prediction. The leftmost column shows predictions using the FlowChain model, showing limited diversity and accuracy for complex trajectories. The middle column presents results from the Augmented-MGF model, which utilizes a mixed Gaussian prior generated from augmented data. This approach significantly improves prediction diversity and accuracy for difficult scenarios. The rightmost column illustrates how adding clusters of augmented data helps generate more diverse and accurate predictions, especially for complex maneuvers like U-turns and sharp turns. Each row represents a different scenario. The numerical values under each column indicate ADE/FDE scores.

More on tables

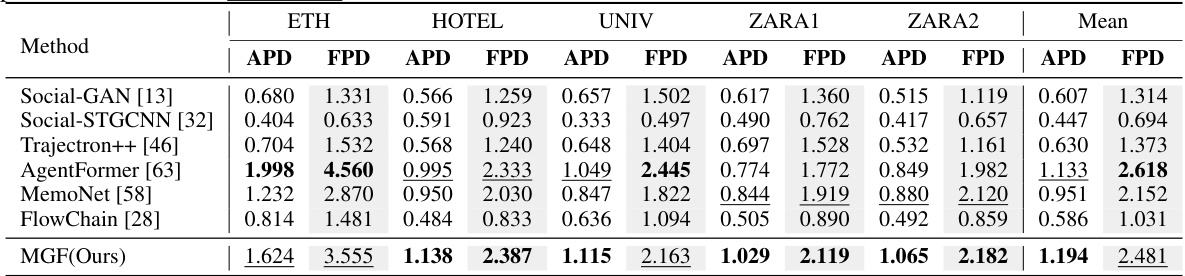
This table presents a comparison of different trajectory prediction models on the ETH/UCY dataset using diversity metrics. Specifically, it shows the Average Pairwise Displacement (APD) and Final Pairwise Displacement (FPD) for each model on five different subsets of the dataset (ETH, HOTEL, UNIV, ZARA1, ZARA2), as well as the average across all subsets. Higher scores indicate greater diversity in the predicted trajectories. The table highlights the best and second-best performing models for each metric and subset.

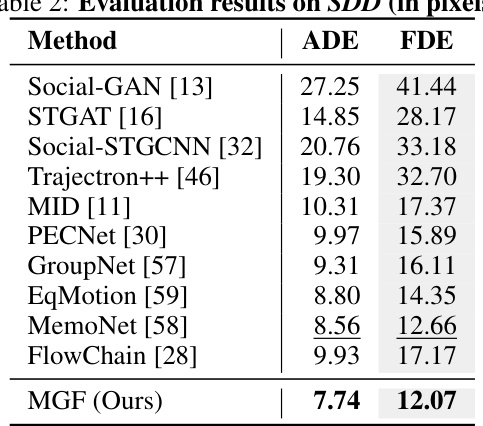
This table presents a comparison of the performance of various trajectory prediction methods on the SDD dataset. The performance is measured using two metrics: Average Displacement Error (ADE) and Final Displacement Error (FDE), both reported in pixels. Lower values indicate better performance. The table shows that the proposed method, MGF, achieves state-of-the-art results, outperforming other methods in both ADE and FDE.

This table presents the ablation study results, showing the impact of different components on the performance metrics ADE and FDE for both ETH/UCY and SDD datasets. Each row represents a different model configuration, systematically removing or adding key components like prediction clustering, mixed Gaussian prior, learnable variance, and inverse loss. The numbers show the ADE and FDE scores. The values in parentheses show the improvement or degradation compared to the baseline model (the first row). A lower value indicates better performance. This table helps to understand the contribution of each component to the overall performance.

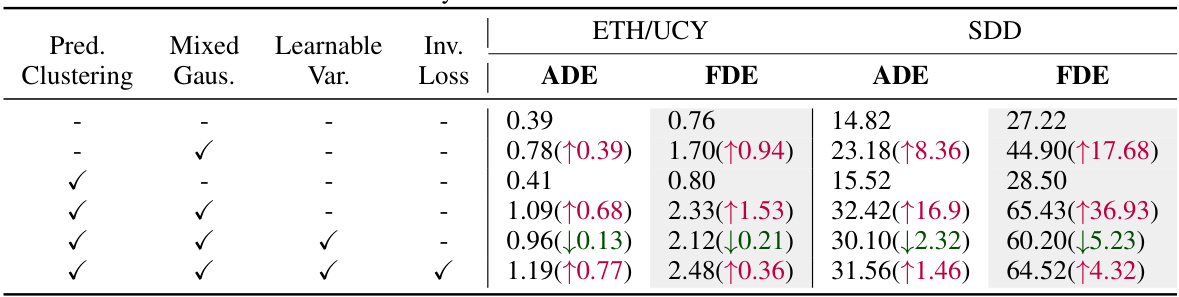
This ablation study investigates the impact of different components on the performance of the model, measured by Average Displacement Error (ADE) and Final Displacement Error (FDE) on the ETH/UCY and SDD datasets. The components evaluated include prediction clustering, a mixed Gaussian prior, learnable variance, and an inverse loss. The results show how each component affects the accuracy and diversity of trajectory prediction.

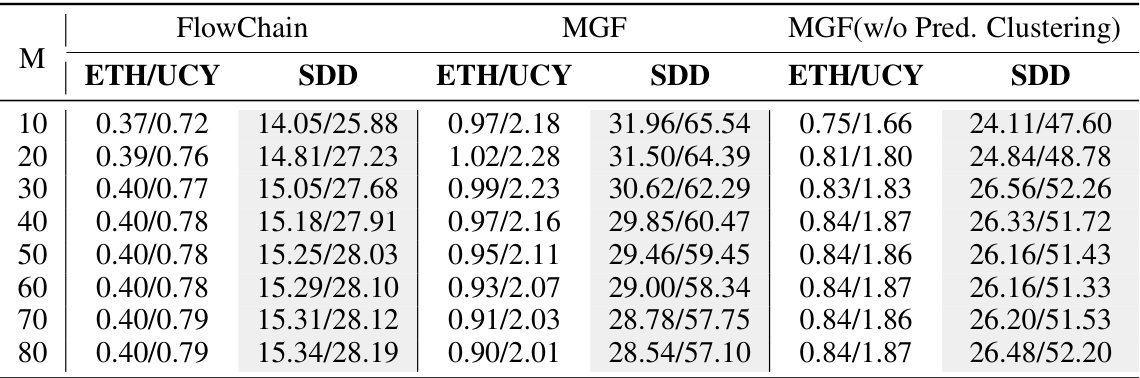
This table presents a comparison of the Average Pairwise Displacement (APD) and Final Pairwise Displacement (FPD) metrics for FlowChain and MGF models across various values of M (number of generated trajectory candidates) on ETH/UCY and SDD datasets. It demonstrates how the diversity metrics change with the number of generated trajectories and how MGF’s performance compares to FlowChain’s.

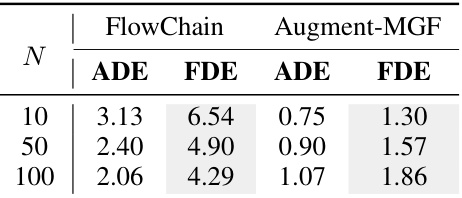
This table presents the minimum average displacement error (minADE) and minimum final displacement error (minFDE) for the worst N predictions on the UNIV dataset. It compares the performance of the FlowChain model with the Augment-MGF model, which incorporates data augmentation to improve performance on challenging scenarios. The results show that Augment-MGF significantly outperforms FlowChain, especially for the worst predictions, highlighting its ability to handle challenging cases better.

Full paper

#