↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many AI tasks involve inference queries expressed as compositions of basic operators on circuit-based representations (e.g., Boolean circuits, probabilistic circuits). Analyzing the tractability of these queries often requires significant effort and is often done on a case-by-case basis. Existing work has focused on specific types of circuits and queries, making it difficult to generalize results.
This research presents a unified compositional inference framework for algebraic circuits, encompassing a broad class of queries (including marginal MAP, probabilistic answer set programming inference, and causal backdoor adjustment). By breaking down complex queries into combinations of basic operators (aggregation, product, elementwise mapping) over semirings, the authors derive novel and general tractability conditions based on circuit properties (e.g., smoothness, decomposability, determinism) and properties of elementwise mappings. The framework unifies existing tractability results and provides a blueprint for analyzing new queries, leading to new tractability conditions for several compositional queries.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with circuit-based representations for inference because it provides a unified framework for analyzing a wide range of compositional queries, leading to more efficient algorithms and a deeper understanding of tractability conditions. It opens new avenues for developing efficient algorithms and exploring the tractability of novel compositional inference queries. This has strong implications for various AI subfields including probabilistic reasoning, causal inference, and knowledge compilation.
Visual Insights#
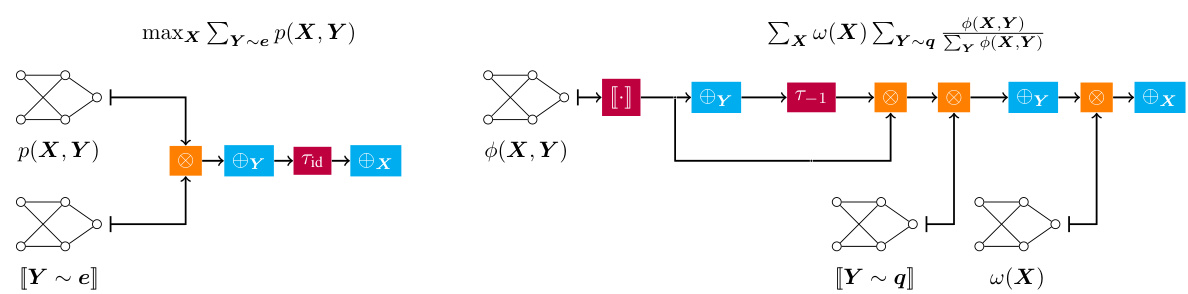
This figure illustrates two example applications of the compositional inference framework presented in the paper. The left side shows how Marginal MAP (MMAP) query can be broken down into a composition of basic operators. MMAP finds the most likely assignment of a subset of variables given some evidence in a probabilistic circuit. The right side illustrates how success probability inference in probabilistic logic programming can also be represented compositionally. This query calculates the probability of a query under a logic program’s semantics (here, MaxEnt), represented as a circuit.

This table presents the tractability conditions for applying basic operations (aggregation, product, and elementwise mapping) to algebraic circuits. It indicates whether the resulting circuit maintains properties such as smoothness, decomposability, and X-determinism, X-compatibility, or X-support compatibility. The complexity of each operation is also specified under various conditions.
In-depth insights#
Compositional Atlas#
A compositional atlas, in the context of a research paper about algebraic circuits, likely refers to a systematic framework for analyzing complex inference queries. It breaks down these queries into basic compositional operators, such as aggregation, product, and elementwise mapping, each with defined tractability conditions and algorithms. This framework serves as a blueprint for analyzing the tractability of novel queries by representing them as compositions of these basic operators and examining if intermediate circuits satisfy the required properties. The core idea is to unify and generalize tractability analysis across various inference problems by identifying shared algebraic structures, reducing the need for instance-specific analysis. This atlas could significantly contribute to AI and machine learning by providing a tool to readily assess the computational feasibility of many inference problems based on easily checkable properties of their corresponding circuits.
Algebraic Circuits#
Algebraic circuits offer a powerful and flexible framework for representing and reasoning with functions over various algebraic structures, such as Boolean functions (in Boolean circuits) or probability distributions (in probabilistic circuits). Their compositional nature enables the decomposition of complex inference tasks into simpler, manageable subproblems, leading to potential efficiency gains. The tractability of inference queries heavily depends on the structural properties of the circuit. Smoothness and decomposability are key properties that ensure efficient marginalization and other operations. The framework also considers properties like determinism and compatibility, which further constrain the structure and impact tractability. This algebraic perspective unifies seemingly disparate inference problems from diverse domains by abstracting away from the specifics of individual semirings, allowing for the derivation of general tractability conditions.
Tractable Inference#
Tractable inference, a critical aspect of AI, focuses on developing efficient algorithms for solving complex inference problems. The core challenge lies in managing the computational complexity that often explodes with the size of the problem. Knowledge compilation translates complex models into more manageable circuit representations, enabling efficient inference queries. Probabilistic circuits are a key example; they compactly represent probability distributions while facilitating tractable computations such as marginalization and model counting. However, many real-world inference tasks involve intricate compositions of operators, going beyond simple marginalization. The research on tractable inference actively explores how such compositional queries can be analyzed and optimized to preserve tractability, employing algebraic structures and circuit properties like smoothness and decomposability. Novel tractability conditions are derived based on circuit structures and operator properties, generalizing previous results for specific queries and semirings. This highlights the power of a compositional inference framework offering a unified approach to systematically handle numerous complex inference problems, improving existing methods and potentially leading to significant advancements in AI systems.
Complexity Analysis#
A thorough complexity analysis is crucial for evaluating the practicality of any algorithm. In the context of this research paper, a complexity analysis would likely focus on the time and space efficiency of the proposed compositional inference framework. This would involve analyzing the computational cost of the basic operators (aggregation, product, and elementwise mapping) and their compositions. Tractability conditions, identified by the authors to ensure efficiency, would be central to the analysis. The analysis should distinguish between the complexity of individual operators and the overall complexity of composed queries, highlighting potential trade-offs between expressiveness and efficiency. Crucially, the analysis must consider the impact of circuit properties (e.g., smoothness, decomposability, determinism) on complexity, demonstrating how these properties enable efficient computation. The analysis should also consider different semirings and their influence on algorithm runtime, demonstrating the framework’s generality. Worst-case and average-case complexities should be addressed, offering a comprehensive assessment of performance, while comparisons to existing algorithms and the discovery of novel complexity bounds for particular inference problems will significantly enhance the contribution.
Future Directions#
Future research could explore extending the compositional framework to encompass more complex queries and a wider range of semirings. Investigating approximate inference methods within this framework is crucial for scalability, particularly for large-scale applications. Developing efficient algorithms for the basic operators and their compositions, especially for cases that don’t fully satisfy the given sufficient conditions, would be highly beneficial. Furthermore, exploring the connections between circuit properties and learnability, focusing on techniques for learning circuits that inherently possess desirable tractability properties, is essential. Combining this work with neural methods could yield powerful hybrid approaches that retain the transparency and tractability of circuit-based models while leveraging the power of neural network learning. Finally, applying the compositional framework to specific real-world applications, such as causal discovery or probabilistic programming, would help to validate its practical utility and identify potential limitations.
More visual insights#
More on figures

The figure contains two examples of algebraic circuits. The first is a Boolean circuit that is smooth, decomposable, and deterministic, but not X-deterministic. The second is a probabilistic circuit that is smooth, decomposable, and X-deterministic. These examples illustrate the concept of algebraic circuits and how different circuit properties can lead to different levels of tractability for various inference tasks. The properties shown are important for the tractability conditions discussed in the paper.

The figure shows a counter-example to demonstrate that even if a Boolean circuit is smooth, decomposable, X-first, and deterministic, the 2AMC algorithm may still return an incorrect result. The example highlights the limitations of relying solely on the X-first property for tractability in 2AMC.
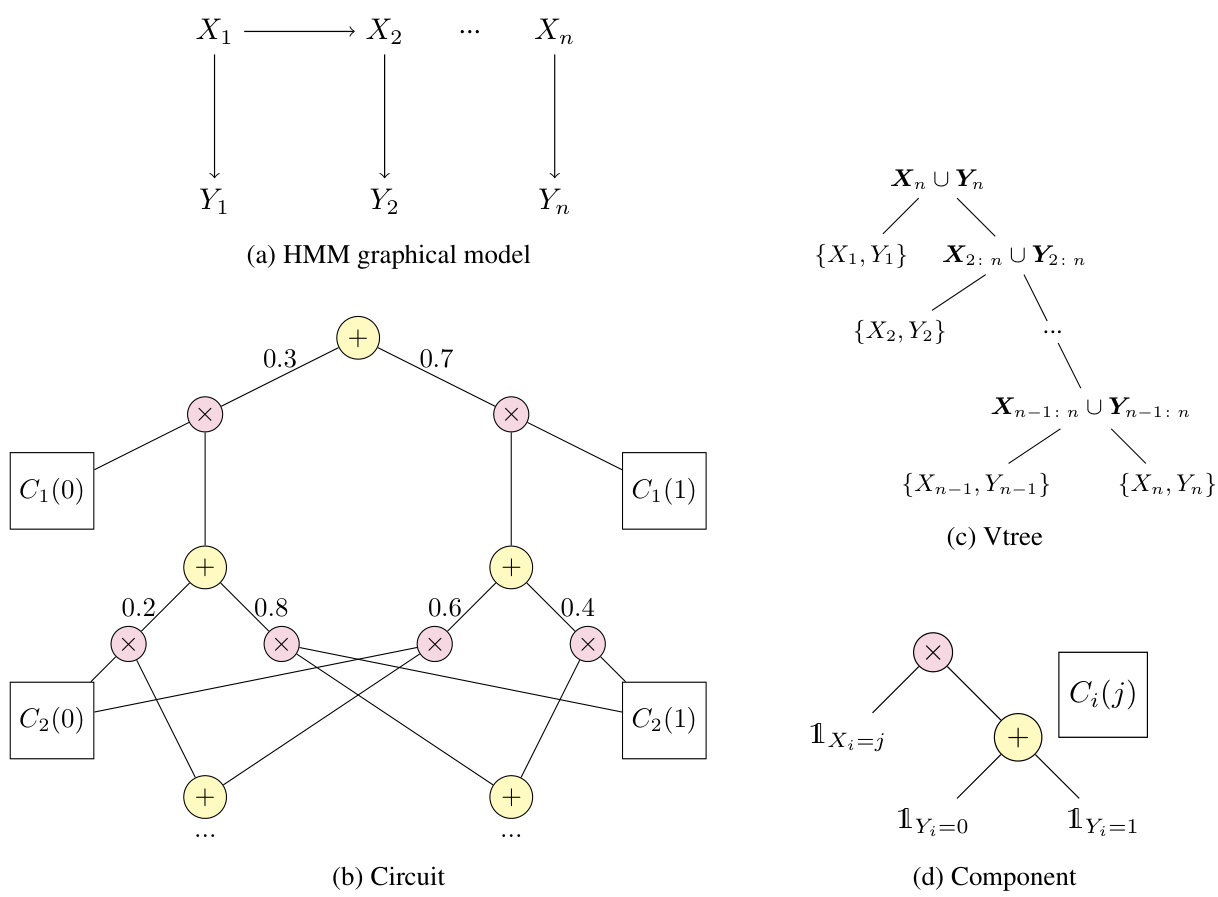
The figure demonstrates how a probabilistic circuit (PC) can represent a hidden Markov model (HMM). Panel (a) shows the graphical model of the HMM, illustrating the dependencies between hidden variables (X) and observed variables (Y). Panel (b) shows the corresponding PC, where nodes represent computations based on the HMM structure. Panel (c) depicts the vtree (variable tree) used to organize the PC construction, indicating how variables are grouped and processed. Panel (d) shows a single component of the PC, outlining the computations performed to calculate a conditional probability. The figure visualizes how the structure of the PC mirrors the HMM’s dependencies, leading to efficient inference.
More on tables
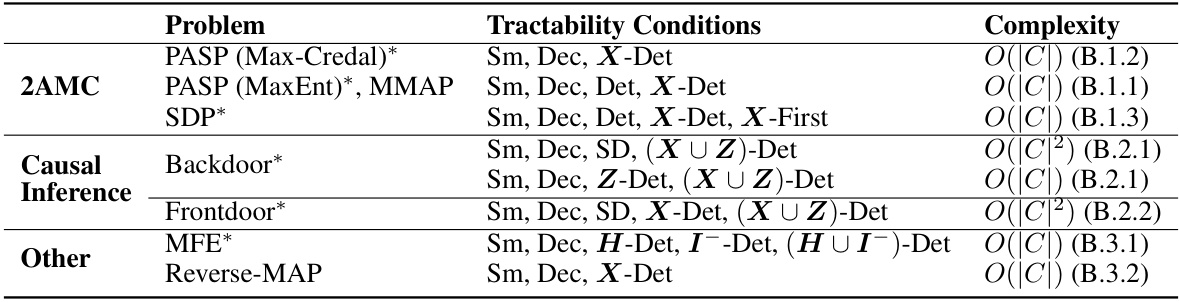
This table summarizes the tractability conditions and time complexity for several compositional inference problems. Each problem is listed, along with the sufficient conditions required for tractable computation using the compositional inference framework described in the paper. These conditions involve properties like smoothness, decomposability, and X-determinism of the circuits used to represent the input functions. The asterisk (*) denotes novel results presented in this work. The complexity is expressed in terms of |C|, representing the size of the circuit.

This table presents the tractability conditions for applying basic operations (aggregation, product, and elementwise mapping) to algebraic circuits. It indicates whether the output circuit maintains certain properties (smoothness, decomposability, X-determinism, X-compatibility, X-support-compatibility) based on the properties of the input circuit(s). The table also specifies the time complexity of each operation.

This table summarizes the tractability conditions and time complexity for various compositional inference problems. It shows the sufficient conditions on the input circuits (smoothness, decomposability, determinism, and compatibility properties) that guarantee tractable computation. The asterisk (*) indicates new results presented in the paper. Problems covered include those from the 2AMC framework, causal inference (backdoor and frontdoor adjustment), and other queries like marginal MAP and MFE.
Full paper#



















