TL;DR#
Fine-tuning large language models is computationally expensive. Parameter-efficient fine-tuning (PEFT) methods, such as adapters and LoRA, offer a solution by updating only a small subset of parameters. However, these methods often have limitations in flexibility and expressiveness. This paper addresses these limitations by introducing Structured Unrestricted-Rank Matrices (SURMs). SURMs leverage structured matrices, offering a balance between compactness and expressiveness, making them a drop-in replacement for existing PEFT methods.
The paper demonstrates SURMs’ effectiveness across various tasks, including image classification and NLP. In image classification, SURMs achieve significant accuracy improvements over baselines while using fewer parameters. In NLP, SURMs show substantial parameter reduction in adapters with minimal performance loss. The results suggest that SURMs offer a promising new paradigm for PEFT, potentially enabling researchers to fine-tune large models more efficiently and effectively.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel approach to parameter-efficient fine-tuning of large language models, addressing the high computational cost of traditional fine-tuning methods. It proposes Structured Unrestricted-Rank Matrices (SURMs), a more flexible and expressive alternative to existing techniques like LoRA and adapters, leading to significant improvements in accuracy and efficiency. This offers a promising avenue for researchers working with large models across various domains.
Visual Insights#

🔼 The left panel shows the approximation error of different matrix types (low-rank, Kronecker product, circulant, Toeplitz) when approximating a positive semi-definite (PSD) matrix. The results indicate that low-rank matrices perform the worst, while circulant and Toeplitz matrices offer better approximations. The right panel illustrates the performance (accuracy) vs. the number of parameters for several parameter-efficient fine-tuning (PEFT) methods on image classification tasks. The authors’ proposed method (SURM) achieves the best performance with a relatively small number of parameters.
read the caption
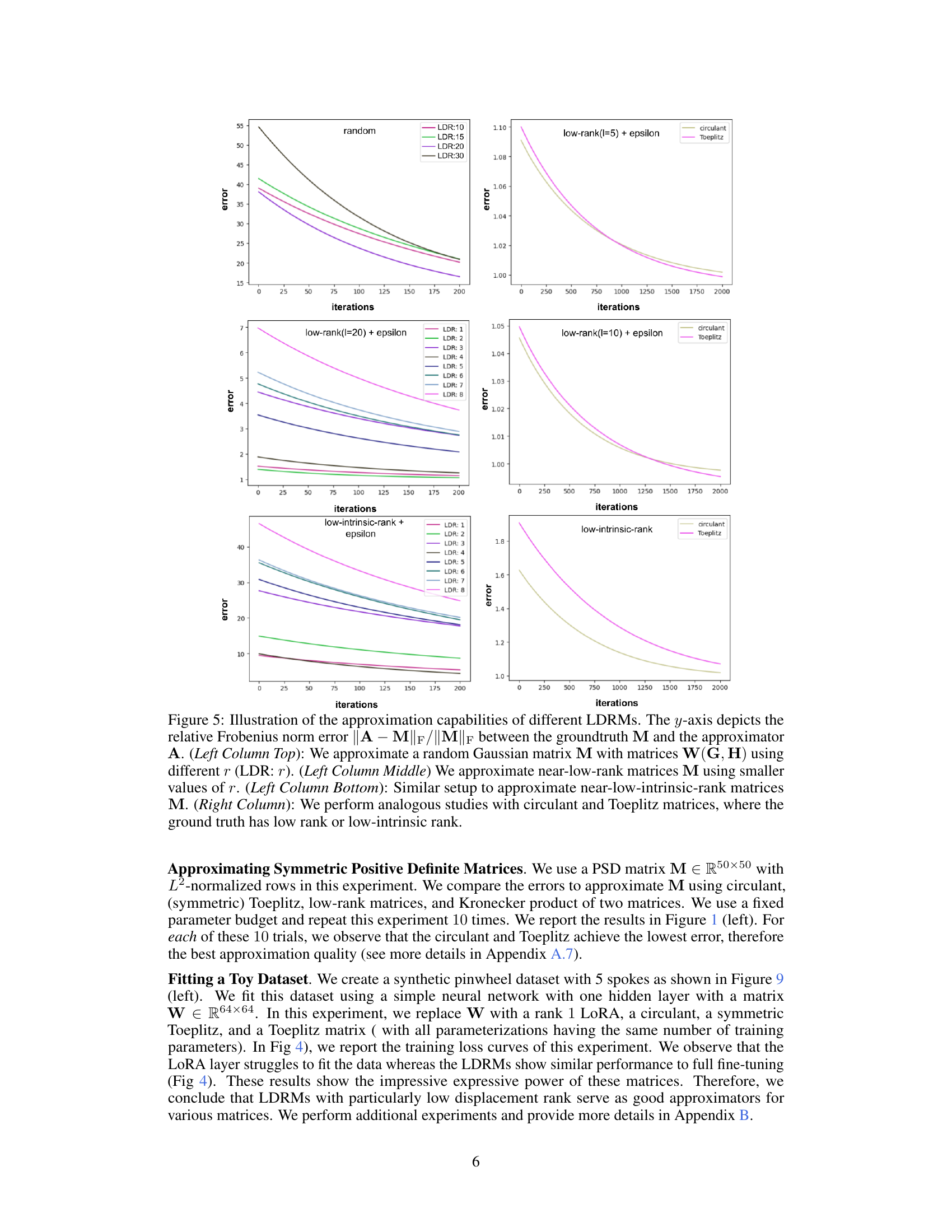
Figure 1: Left: Approximating a PSD matrix using a low rank matrix, Kronecker product of matrices, circulant matrix, and Toeplitz matrix. We repeat our experiment 10 times and for each trial, we observe that low rank matrix is the worst approximator followed by Kronecker product, circulant, and Toeplitz. Right: The tradeoff between accuracy and parameter numbers of various PEFT methods. Results are measured across 5 image datasets using CLIP-ViT. Our methods appear in the top right corner (in blue) and achieve the best performance among various strong baseline methods.
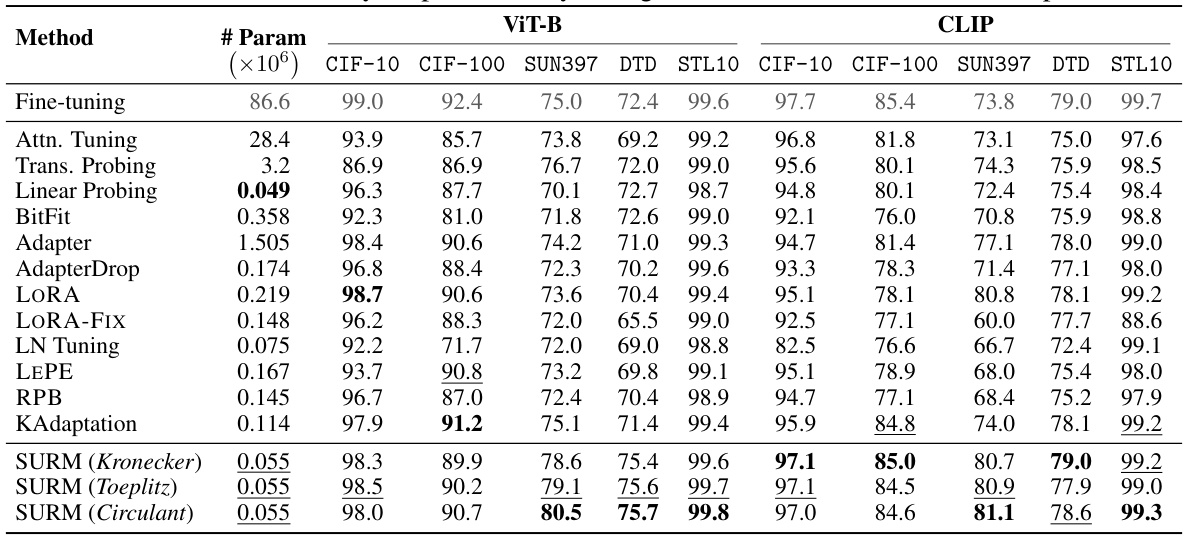
🔼 This table presents the results of experiments using Vision Transformers (ViT) on various image classification datasets (CIFAR-10, CIFAR-100, SUN397, DTD, STL10). It compares the performance of the proposed Structured Unrestricted-Rank Matrices (SURM) method with several other parameter-efficient fine-tuning (PEFT) baselines, including Attention Tuning, Linear Probing, BitFit, Adapter, AdapterDrop, LoRA, LoRA-FIX, LN Tuning, LEPE, RPB, KAdaptation. The table shows the number of parameters used by each method and the accuracy achieved on each dataset. The results demonstrate that SURM consistently achieves higher accuracy than the baselines while using significantly fewer parameters.
read the caption
Table 1: ViT-experiments : Baseline numbers are taken from [24]. The best numbers are highlighted in bold and the second-best numbers are underlined. Hyperparameter settings are followed from [24]. We find that SURM consistently outperform very strong baselines with 2-3x reduction in parameters.
In-depth insights#
SURM: A New PEFT#
The proposed Structured Unrestricted-Rank Matrices (SURM) offer a novel approach to Parameter-Efficient Fine-Tuning (PEFT) of large language models. Unlike existing PEFT methods that rely on low-rank approximations, often limiting expressiveness, SURM leverages structured matrices with unrestricted rank, achieving a balance between compactness and expressiveness. This is demonstrated through its ability to effectively approximate various matrix classes, outperforming low-rank alternatives in several experiments. SURM’s flexibility allows for drop-in replacement of existing PEFT techniques like adapters and LoRA, yielding significant improvements, particularly in terms of accuracy gains and parameter reduction. The method’s efficacy is validated across various downstream tasks and datasets, showcasing its potential as a robust and versatile PEFT framework. Key advantages include improved approximation capabilities and the flexibility to adjust the balance between compactness and expressiveness. However, future research should explore its computational cost in larger-scale deployments and further assess its effectiveness across an even broader range of model architectures and tasks.
LDR Matrix Analysis#
An analysis of Low Displacement Rank (LDR) matrices within the context of a research paper would likely explore their properties as approximators of arbitrary matrices. The core focus would be on demonstrating the effectiveness of LDR matrices in parameter-efficient fine-tuning of large language models. Key aspects would include evaluating the trade-off between approximation accuracy and the number of parameters required to represent the LDR matrix, comparing its performance against other matrix approximation methods (e.g., low-rank matrices), and investigating the impact of different LDR matrix structures (e.g., circulant, Toeplitz) on approximation quality. A crucial element would be showcasing the computational advantages of LDR matrices, highlighting their efficiency in matrix-vector multiplication, which is key to the speed and scalability of the model fine-tuning process. The analysis might also explore theoretical justifications for the effectiveness of LDR matrices, potentially linking their properties to the intrinsic dimensionality of the data representations within the neural network. Specific experiments would likely involve approximating randomly generated matrices, low-rank matrices, or matrices from real-world datasets using different types of LDR matrices and comparing the results. The ultimate goal would be to establish the value proposition of using LDR matrices in this context, showing that they offer a balance between expressiveness and compactness, surpassing alternative methods in terms of parameter efficiency and potentially accuracy.
Vision & NLP tasks#
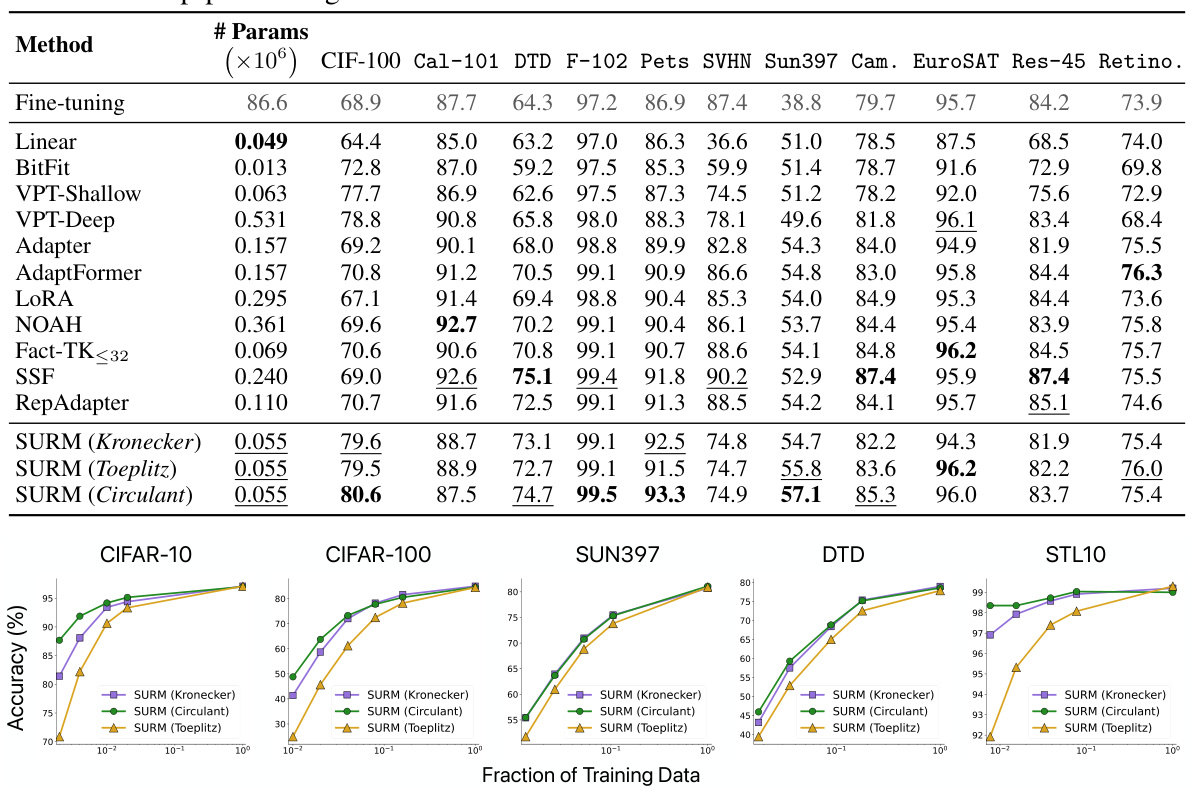
This research paper explores parameter-efficient fine-tuning (PEFT) methods for large Transformer models, focusing on vision and natural language processing (NLP) tasks. The core contribution is the introduction of Structured Unrestricted-Rank Matrices (SURMs) as a novel PEFT approach. SURMs offer more flexibility than existing methods like LoRA and Adapters by leveraging structured matrices, enabling a better balance between compactness and expressiveness. The authors demonstrate the effectiveness of SURMs across various vision datasets (CIFAR-10, CIFAR-100, SUN397, etc.) and NLP benchmarks (GLUE). Significant performance improvements are observed compared to baselines, often with a substantial reduction in the number of trainable parameters. The study also investigates the approximation capabilities of SURMs, showing their ability to approximate various matrix classes effectively. SURMs demonstrate impressive performance even in low-resource settings, achieving high accuracy with a small fraction of training data. Overall, the paper presents a compelling case for SURMs as a highly competitive PEFT technique with significant potential for various applications.
Low-Resource Tuning#
Low-resource tuning tackles the challenge of adapting large language models (LLMs) to downstream tasks with limited training data. This is critical as acquiring substantial labeled data for every task is often infeasible. The core idea is to maximize performance with minimal data, addressing the overparameterization issue of LLMs. Effective low-resource tuning methods modify only a small subset of parameters, thereby reducing computational costs and memory requirements. Key strategies involve techniques like parameter-efficient fine-tuning (PEFT), focusing on updating only adapter layers or employing low-rank updates instead of full fine-tuning. Successful approaches often leverage structured matrices or other compact parameterizations to represent model updates, significantly reducing the number of trainable parameters while preserving model expressiveness. The effectiveness of low-resource tuning is typically evaluated on benchmark datasets, demonstrating accuracy comparable to full fine-tuning while using a fraction of training data. This research area remains very active due to the practical importance of efficient and sustainable LLM adaptation.
Future Works#
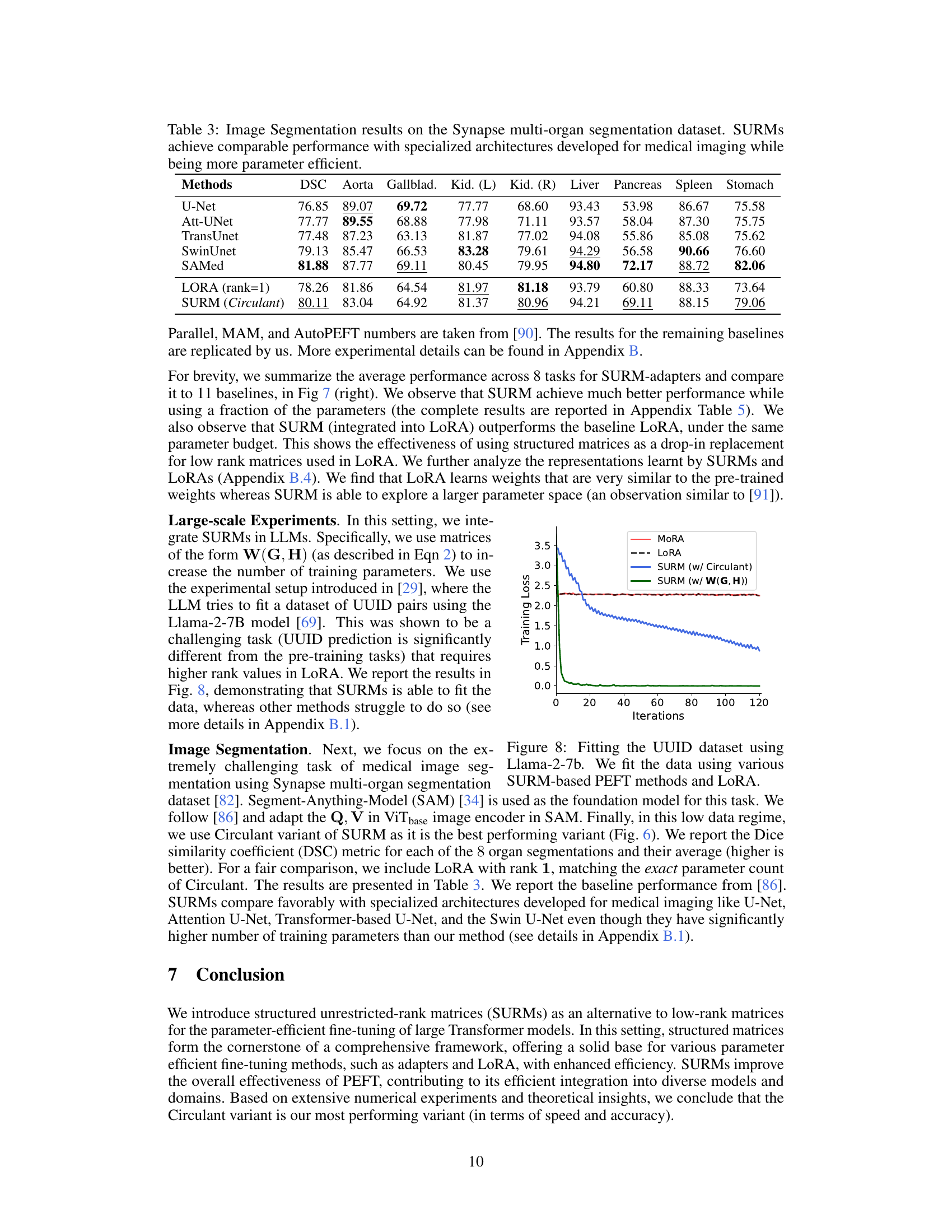
Future research directions stemming from this paper on structured unrestricted-rank matrices (SURMs) for parameter-efficient fine-tuning could explore several promising avenues. Extending SURMs to other architectural designs beyond transformers is crucial to assess their broader applicability. Investigating the impact of different SURM types (circulant, Toeplitz, Kronecker) across various tasks and model sizes warrants further study, potentially revealing task-specific optimal structures. The development of more efficient algorithms for SURM-based matrix operations, potentially leveraging specialized hardware or approximation techniques, could significantly improve computational efficiency. A deeper exploration into the theoretical understanding of SURMs’ approximation capabilities, perhaps by connecting them to low-rank matrix properties, could provide valuable insights. Finally, combining SURMs with other PEFT techniques such as adapters or prompt tuning could unlock enhanced performance and efficiency, while studying the impact of SURMs on model robustness and generalization is necessary.
More visual insights#
More on figures

🔼 The figure demonstrates the approximation capabilities of different matrix types (low-rank, Kronecker product, circulant, Toeplitz) and their performance in parameter-efficient fine-tuning (PEFT). The left panel shows that structured unrestricted-rank matrices (SURMs), particularly circulant and Toeplitz matrices, offer better approximations than low-rank matrices. The right panel compares the accuracy and parameter count of SURMs against other PEFT methods on image classification tasks, highlighting the superior performance and efficiency of SURMs.
read the caption
Figure 1: Left: Approximating a PSD matrix using a low rank matrix, Kronecker product of matrices, circulant matrix, and Toeplitz matrix. We repeat our experiment 10 times and for each trial, we observe that low rank matrix is the worst approximator followed by Kronecker product, circulant, and Toeplitz. Right: The tradeoff between accuracy and parameter numbers of various PEFT methods. Results are measured across 5 image datasets using CLIP-ViT. Our methods appear in the top right corner (in blue) and achieve the best performance among various strong baseline methods.

🔼 This figure demonstrates that a circulant matrix can be decomposed into a linear combination of orthogonal base circulant matrices. The figure visually shows this decomposition for a 5x5 matrix, highlighting that each base matrix has only one non-zero entry in each column. However, this closed-form decomposition is not generally possible for all matrices; therefore, finding optimal approximators for arbitrary matrices often requires gradient descent methods.
read the caption
Figure 3: A circulant matrix with the first column given by a vector (C0, C1, C2, C3, C4) can be re-written as a linear combination of the orthogonal base circulant matrices (5 matrices with orange-entries corresponding to one and other to zero). Such a closed-form decomposition is in general not possible for matrices W(G, H) and thus optimal approximators are found by gradient-descent.

🔼 The left panel demonstrates the approximation capabilities of different matrix types (low-rank, Kronecker product, circulant, Toeplitz) for approximating a positive semi-definite (PSD) matrix. The results show that low-rank matrices perform worst, followed by Kronecker product, circulant, and Toeplitz matrices. The right panel illustrates the trade-off between model accuracy and the number of parameters for various parameter-efficient fine-tuning (PEFT) methods on five image datasets using CLIP-ViT. The proposed SURM methods achieve the highest accuracy while using fewer parameters.
read the caption
Figure 1: Left: Approximating a PSD matrix using a low rank matrix, Kronecker product of matrices, circulant matrix, and Toeplitz matrix. We repeat our experiment 10 times and for each trial, we observe that low rank matrix is the worst approximator followed by Kronecker product, circulant, and Toeplitz. Right: The tradeoff between accuracy and parameter numbers of various PEFT methods. Results are measured across 5 image datasets using CLIP-ViT. Our methods appear in the top right corner (in blue) and achieve the best performance among various strong baseline methods.

🔼 The left panel shows the approximation error of different matrix types when approximating a positive semi-definite (PSD) matrix. Low-rank matrices perform worst, followed by Kronecker product, circulant, and Toeplitz matrices. The right panel illustrates the accuracy vs. the number of parameters for various parameter-efficient fine-tuning (PEFT) methods across five image datasets using the CLIP-ViT model. The proposed SURM methods achieve superior performance.
read the caption
Figure 1: Left: Approximating a PSD matrix using a low rank matrix, Kronecker product of matrices, circulant matrix, and Toeplitz matrix. We repeat our experiment 10 times and for each trial, we observe that low rank matrix is the worst approximator followed by Kronecker product, circulant, and Toeplitz. Right: The tradeoff between accuracy and parameter numbers of various PEFT methods. Results are measured across 5 image datasets using CLIP-ViT. Our methods appear in the top right corner (in blue) and achieve the best performance among various strong baseline methods.
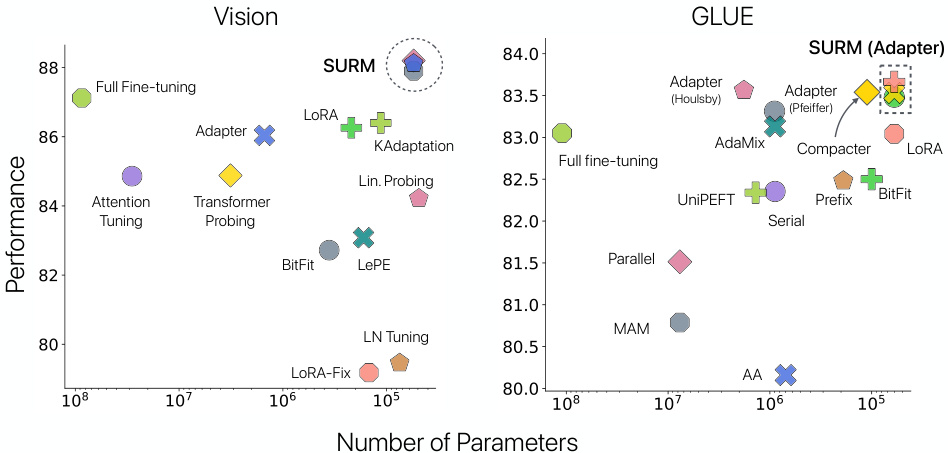
🔼 This figure showcases the trade-off between performance and the number of parameters used for various parameter-efficient fine-tuning (PEFT) methods on image classification and GLUE benchmark datasets. The left panel shows results for five image datasets using the ViT-B model. The right panel shows GLUE benchmark results. In both cases, the SURM methods (structured unrestricted-rank matrices) are shown to achieve the best performance, particularly in terms of accuracy given a relatively small parameter count. This highlights SURM’s efficiency compared to other PEFT techniques such as adapters and LoRA.
read the caption
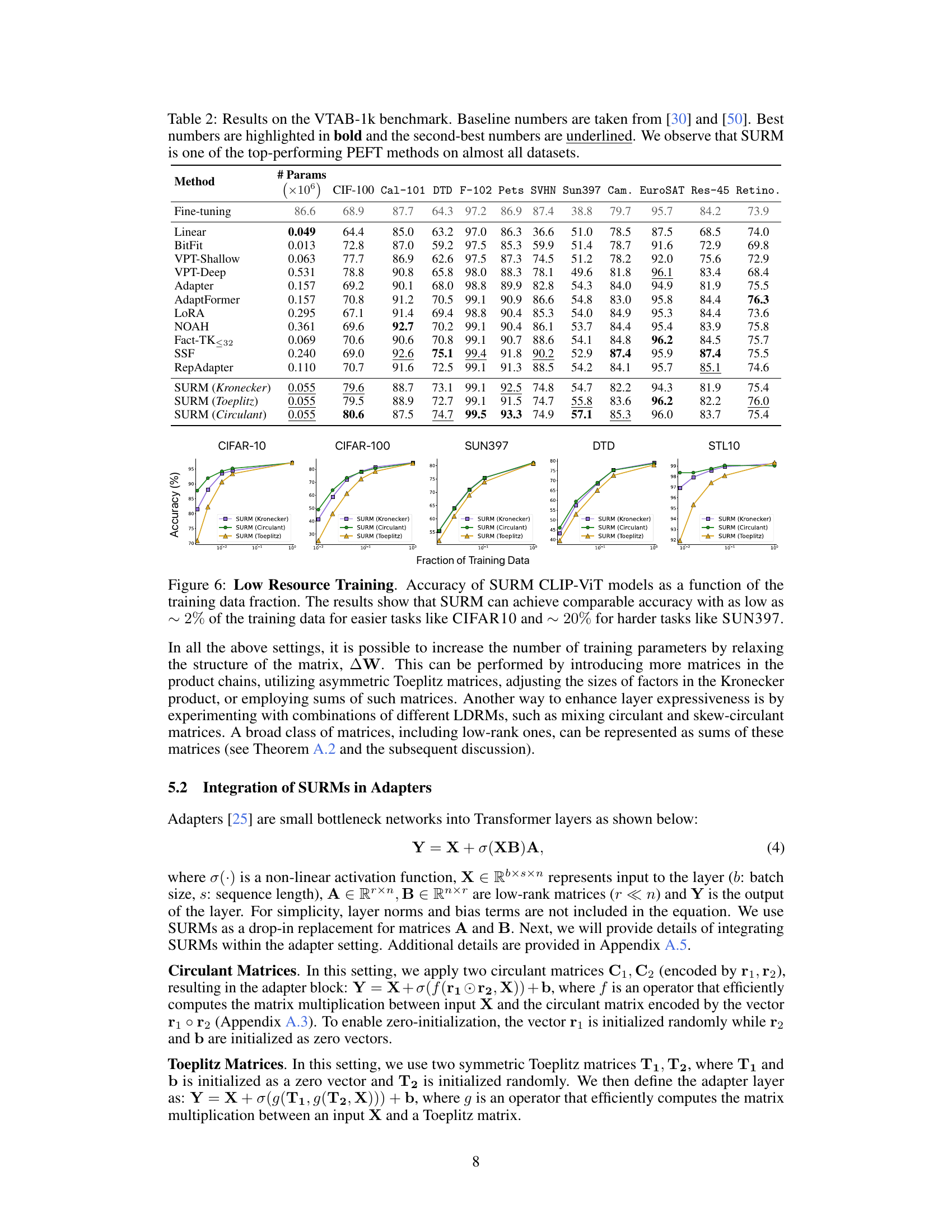
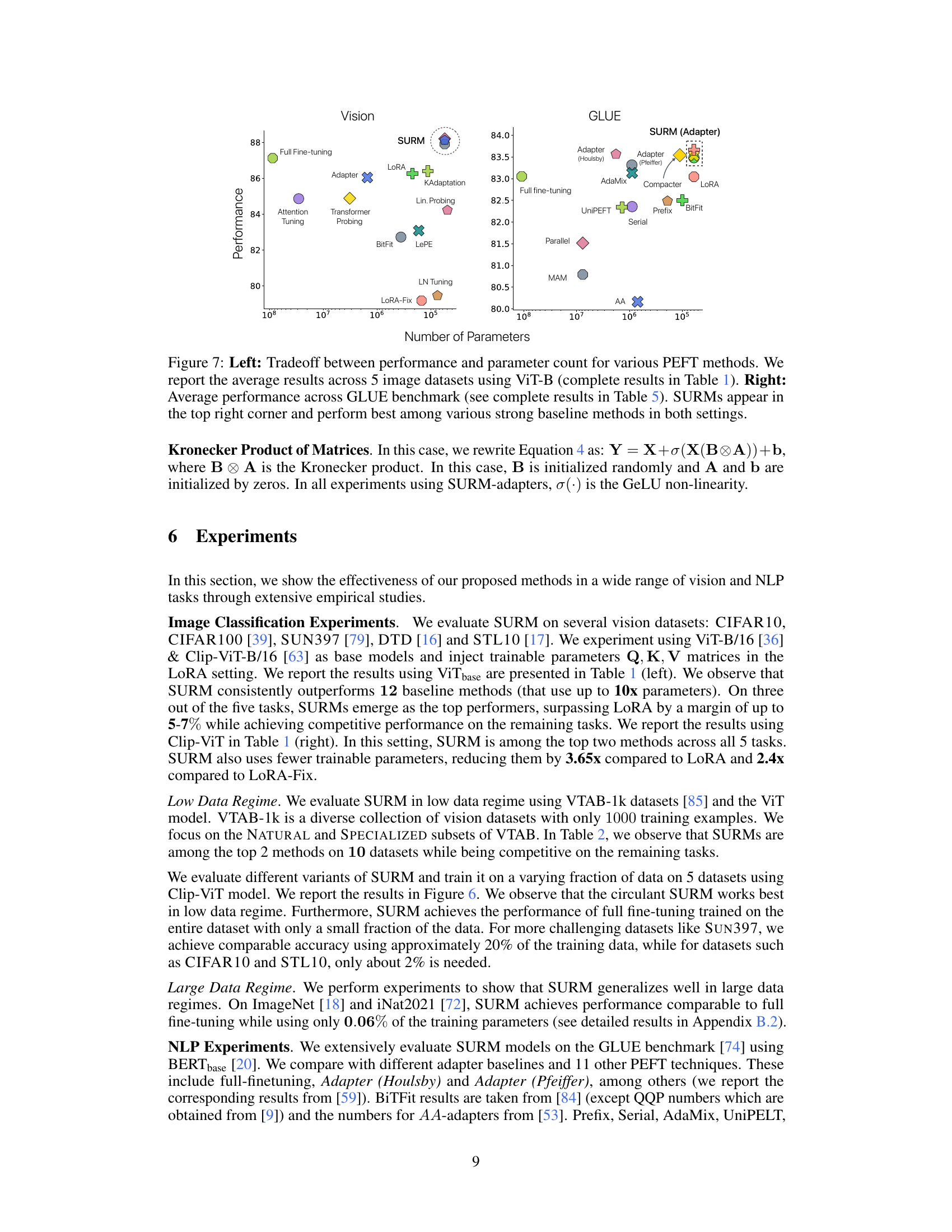
Figure 7: Left: Tradeoff between performance and parameter count for various PEFT methods. We report the average results across 5 image datasets using ViT-B (complete results in Table 1). Right: Average performance across GLUE benchmark (see complete results in Table 5). SURMs appear in the top right corner and perform best among various strong baseline methods in both settings.

🔼 The left panel shows the approximation error of different matrix types when approximating a positive semi-definite (PSD) matrix. Low-rank matrices perform worst, followed by Kronecker product, circulant, and Toeplitz matrices. The right panel displays the accuracy vs. parameter count tradeoff of different parameter-efficient fine-tuning (PEFT) methods on five image datasets using CLIP-ViT. The proposed SURM method shows a good balance between high accuracy and a low number of parameters.
read the caption
Figure 1: Left: Approximating a PSD matrix using a low rank matrix, Kronecker product of matrices, circulant matrix, and Toeplitz matrix. We repeat our experiment 10 times and for each trial, we observe that low rank matrix is the worst approximator followed by Kronecker product, circulant, and Toeplitz. Right: The tradeoff between accuracy and parameter numbers of various PEFT methods. Results are measured across 5 image datasets using CLIP-ViT. Our methods appear in the top right corner (in blue) and achieve the best performance among various strong baseline methods.

🔼 The left panel shows a comparison of the approximation error of different matrix types (low-rank, Kronecker product, circulant, Toeplitz) when approximating a positive semi-definite (PSD) matrix. The results demonstrate that structured matrices like circulant and Toeplitz offer better approximations than low-rank matrices. The right panel illustrates the accuracy vs. parameter count trade-off for various parameter-efficient fine-tuning (PEFT) methods on image classification tasks. It highlights that the proposed Structured Unrestricted-Rank Matrices (SURMs) achieve high accuracy with a relatively small number of parameters, outperforming existing PEFT techniques.
read the caption
Figure 1: Left: Approximating a PSD matrix using a low rank matrix, Kronecker product of matrices, circulant matrix, and Toeplitz matrix. We repeat our experiment 10 times and for each trial, we observe that low rank matrix is the worst approximator followed by Kronecker product, circulant, and Toeplitz. Right: The tradeoff between accuracy and parameter numbers of various PEFT methods. Results are measured across 5 image datasets using CLIP-ViT. Our methods appear in the top right corner (in blue) and achieve the best performance among various strong baseline methods.
🔼 The figure on the left compares the approximation error of different matrix types (low-rank, Kronecker product, circulant, and Toeplitz) when approximating a positive semi-definite (PSD) matrix. It shows that low-rank matrices have the highest error, while Toeplitz matrices have the lowest. The figure on the right shows a comparison of parameter-efficient fine-tuning (PEFT) methods in terms of accuracy versus the number of parameters. The authors’ method (SURM) achieves the best performance, demonstrating a good balance between accuracy and compactness.
read the caption
Figure 1: Left: Approximating a PSD matrix using a low rank matrix, Kronecker product of matrices, circulant matrix, and Toeplitz matrix. We repeat our experiment 10 times and for each trial, we observe that low rank matrix is the worst approximator followed by Kronecker product, circulant, and Toeplitz. Right: The tradeoff between accuracy and parameter numbers of various PEFT methods. Results are measured across 5 image datasets using CLIP-ViT. Our methods appear in the top right corner (in blue) and achieve the best performance among various strong baseline methods.

🔼 The left panel shows a comparison of the approximation error for different matrix types when approximating a positive semidefinite (PSD) matrix. The right panel illustrates the trade-off between accuracy and the number of parameters for different parameter-efficient fine-tuning (PEFT) methods on five image datasets using CLIP-ViT. The authors’ method (SURM) achieves the highest accuracy with a relatively low number of parameters.
read the caption
Figure 1: Left: Approximating a PSD matrix using a low rank matrix, Kronecker product of matrices, circulant matrix, and Toeplitz matrix. We repeat our experiment 10 times and for each trial, we observe that low rank matrix is the worst approximator followed by Kronecker product, circulant, and Toeplitz. Right: The tradeoff between accuracy and parameter numbers of various PEFT methods. Results are measured across 5 image datasets using CLIP-ViT. Our methods appear in the top right corner (in blue) and achieve the best performance among various strong baseline methods.
More on tables
🔼 This table presents the results of experiments on various image classification datasets using Vision Transformers (ViTs). The table compares the performance of the proposed Structured Unrestricted-Rank Matrices (SURM) method against several baseline parameter-efficient fine-tuning (PEFT) techniques. The performance is measured in terms of accuracy across different datasets (CIFAR-10, CIFAR-100, SUN397, DTD, STL10). The number of parameters used by each method is also reported. The table highlights that SURM achieves better accuracy than the baselines while using significantly fewer parameters.
read the caption
Table 1: ViT-experiments : Baseline numbers are taken from [24]. The best numbers are highlighted in bold and the second-best numbers are underlined. Hyperparameter settings are followed from [24]. We find that SURM consistently outperform very strong baselines with 2-3x reduction in parameters.
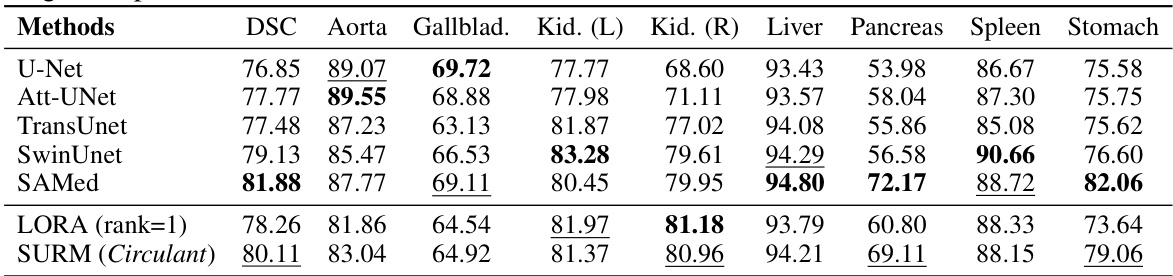
🔼 This table presents the results of experiments using Vision Transformers (ViTs) on various image classification datasets (CIFAR-10, CIFAR-100, SUN397, DTD, STL-10). It compares the performance of the proposed Structured Unrestricted-Rank Matrices (SURM) method against several baselines, including fine-tuning, attention tuning, linear probing, adapter methods, and LoRA. The table shows the accuracy achieved by each method, along with the number of parameters used. SURM demonstrates improved accuracy with significantly fewer parameters compared to baseline methods.
read the caption
Table 1: ViT-experiments : Baseline numbers are taken from [24]. The best numbers are highlighted in bold and the second-best numbers are underlined. Hyperparameter settings are followed from [24]. We find that SURM consistently outperform very strong baselines with 2-3x reduction in parameters.

🔼 This table presents the results of experiments conducted on various image classification datasets using Vision Transformers (ViTs). It compares the performance of the proposed Structured Unrestricted-Rank Matrices (SURM) method against several baseline parameter-efficient fine-tuning (PEFT) techniques. The table shows accuracy results on multiple datasets (CIFAR-10, CIFAR-100, SUN397, DTD, STL10) for both ViT-B and CLIP architectures. The number of parameters used by each method is also provided, highlighting SURM’s efficiency in achieving competitive or better accuracy with significantly fewer parameters.
read the caption
Table 1: ViT-experiments : Baseline numbers are taken from [24]. The best numbers are highlighted in bold and the second-best numbers are underlined. Hyperparameter settings are followed from [24]. We find that SURM consistently outperform very strong baselines with 2-3x reduction in parameters.
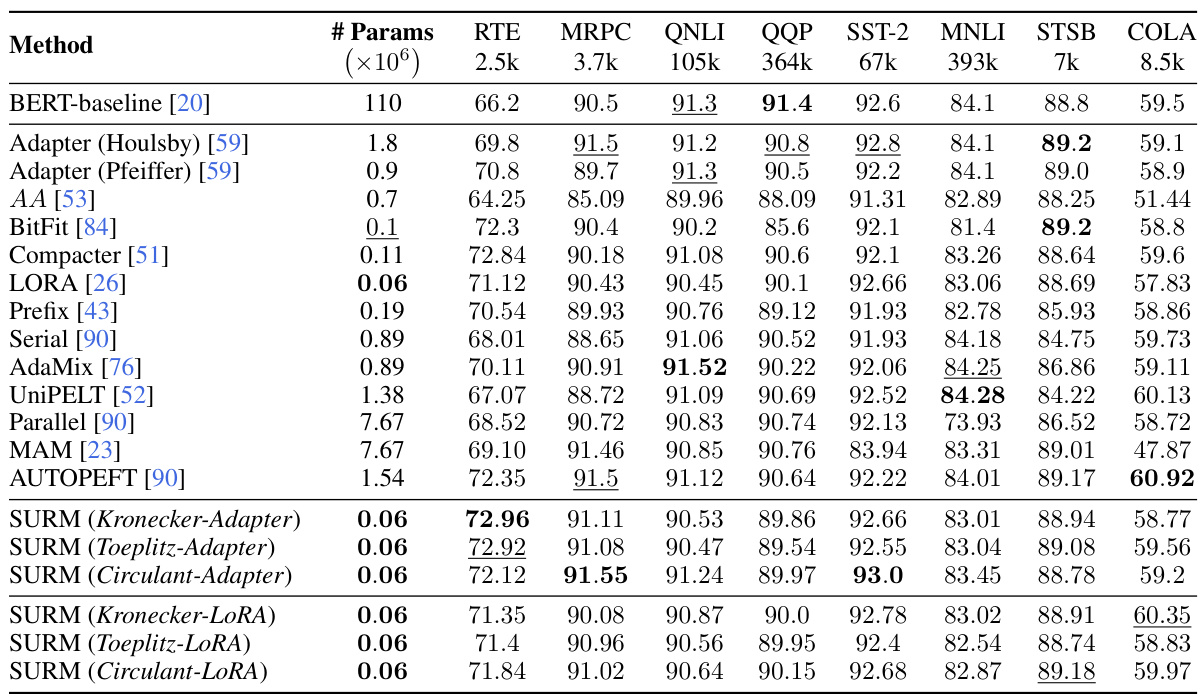
🔼 This table presents the performance comparison of the proposed Structured Unrestricted-Rank Matrices (SURMs) method against various other parameter-efficient fine-tuning (PEFT) techniques on the GLUE benchmark dataset. The table shows the scores (MCC, F1, Spearman correlation, and Accuracy) achieved by each method across different GLUE tasks. The number of parameters used by each method is also indicated.
read the caption
Table 5: Performance of SURM and other baselines on GLUE benchmark. We report the MCC score for COLA, F1 score for MRPC, Spearman correlation for STSB, and accuracy scores for the other tasks. All results are obtained by averaging over 3 seeds. Best numbers are highlighted in bold and the second best numbers is underline.

🔼 This table presents the results of image classification experiments using Vision Transformers (ViT). It compares the performance of the proposed Structured Unrestricted-Rank Matrices (SURM) method against several baseline parameter-efficient fine-tuning (PEFT) techniques across five image datasets (CIFAR-10, CIFAR-100, SUN397, DTD, STL10). The table shows the accuracy achieved by each method, the number of parameters used, and highlights the best and second-best results for each dataset. The results demonstrate that SURM achieves higher accuracy than baselines while using significantly fewer parameters.
read the caption
Table 1: ViT-experiments : Baseline numbers are taken from [24]. The best numbers are highlighted in bold and the second-best numbers are underlined. Hyperparameter settings are followed from [24]. We find that SURM consistently outperform very strong baselines with 2-3x reduction in parameters.

🔼 This table presents the results of various parameter-efficient fine-tuning (PEFT) methods on the GLUE benchmark. It compares the performance of Structured Unrestricted-Rank Matrices (SURMs) against several other PEFT techniques, including LoRA and adapter-based methods. The metrics used include Matthews Correlation Coefficient (MCC), F1-score, Spearman correlation, and accuracy, depending on the specific task. The number of parameters used by each method is also shown, demonstrating the parameter efficiency of SURMs.
read the caption
Table 5: Performance of SURM and other baselines on GLUE benchmark. We report the MCC score for COLA, F1 score for MRPC, Spearman correlation for STSB, and accuracy scores for the other tasks. All results are obtained by averaging over 3 seeds. Best numbers are highlighted in bold and the second best numbers is underline.

🔼 This table shows the Centered Kernel Alignment (CKA) scores between the full fine-tuned weights and the weights obtained using different structured unrestricted rank matrices (SURMs) – LoRA, Circulant, Symmetric Toeplitz, and Toeplitz. CKA measures the similarity between two sets of feature vectors. Higher CKA scores indicate greater similarity. The table demonstrates that SURM methods, particularly the circulant variant, achieve substantially higher CKA scores compared to LoRA, suggesting that SURMs learn representations that are more similar to those learned by full fine-tuning.
read the caption
Table 8: CKA between full finetuned weights and the SURM weights
Full paper#