TL;DR#
Imputing missing values in functional data, crucial for many applications, is challenging, especially when data is sparse and noisy. Traditional statistical methods like PACE often struggle with complex data structures and noise. Neural network-based methods, while promising, often lack the ability to ensure the smoothness and continuity of the imputed function. This necessitates the use of penalties or post-processing steps like kernel smoothing which may impact performance.
The paper introduces SAND, a novel method that augments transformer networks with a ‘self-attention on derivatives’ module. This module explicitly encourages smoothness by modeling the sub-derivative of the curve, resulting in improved imputation accuracy and better handling of noisy data. Extensive experiments demonstrate that SAND outperforms traditional statistical methods and vanilla transformer networks, providing a more robust and accurate approach for functional data imputation.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly improves the accuracy of functional data imputation, a crucial task in many fields. It introduces a novel method that outperforms existing techniques, particularly for sparsely observed data. This opens new avenues for research in deep learning for functional data and has broader implications for various applications relying on functional data analysis.
Visual Insights#

🔼 This figure illustrates the SAND (Self-Attention on Derivatives) pipeline. It starts with a vanilla transformer that produces an initial imputation. The SAND module then takes this initial imputation and calculates its derivative using the Diff operator. The resulting derivative is then integrated using the Intg operator to produce a smoother, refined imputation. The figure visually depicts how the SAND module refines the initial, often noisy imputation, resulting in a smoother curve that better fits the underlying data.
read the caption
Figure 2: SAND's pipeline. Dashed lines are underlying processes, dots are observations sampled with errors, solid red curves are imputations, and solid orange curves are learned derivatives.
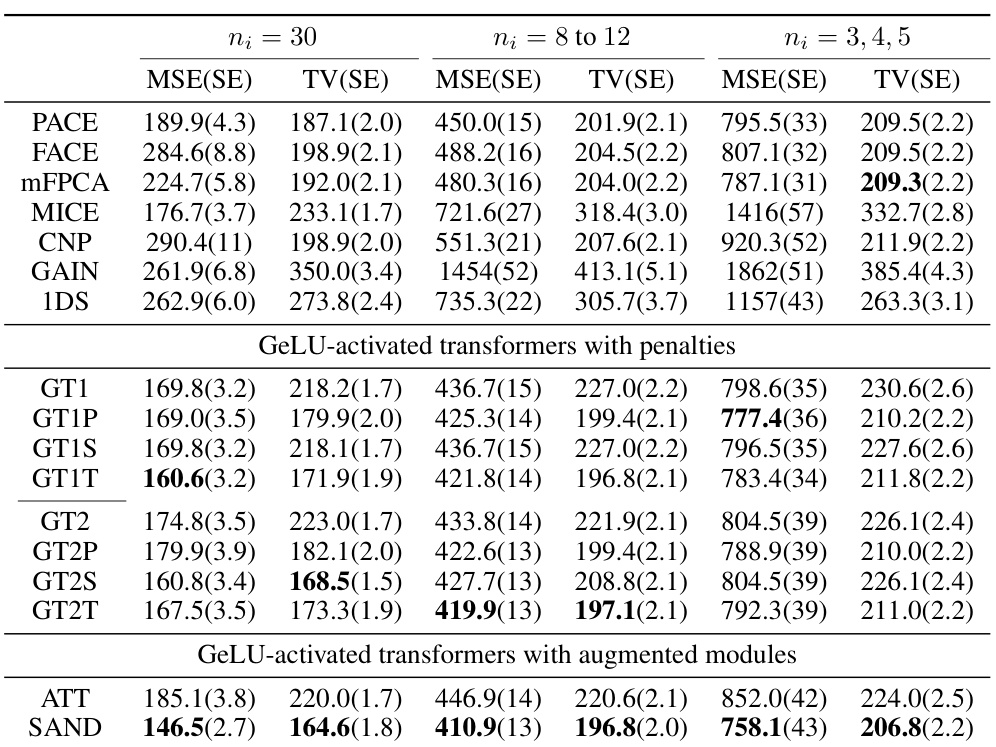
🔼 This table presents the Mean Squared Error (MSE) and Total Variation (TV) along with their standard errors (SE) for different methods on simulated data. Three different scenarios are shown, with varying numbers of observations per subject (ni): 30, 8 to 12, and 3, 4, 5. The methods compared include PACE, FACE, mFPCA, MICE, CNP, GAIN, 1DS, and various transformer-based models (GT1, GT1P, GT1S, GT1T, GT2, GT2P, GT2S, GT2T, ATT, and SAND). Bold values highlight the top two performing methods for each scenario. The table allows for a comparison of imputation accuracy and smoothness across different methods and data sparsity levels.
read the caption
Table 1: MSE(SE) & TV(SE) on simulated data. Bold values indicate the top 2 performing methods.
In-depth insights#
Transformer Imputation#
Transformer imputation leverages the power of transformer networks, renowned for their success in natural language processing and computer vision, to address the challenge of imputing missing values in functional data. Unlike traditional methods that often rely on strong assumptions or struggle with irregularly spaced data, transformer imputation models the underlying functional relationships, particularly benefiting from the self-attention mechanism. This mechanism allows the model to effectively capture long-range dependencies and complex patterns within the data, leading to more accurate and robust estimations. However, vanilla transformers may generate non-smooth imputations. Advanced techniques, such as incorporating self-attention on derivatives (SAND), are being developed to address this limitation and to incorporate the inductive bias of smoothness, ultimately leading to smoother and more interpretable results. The theoretical underpinnings of these approaches are crucial for ensuring the reliability and generalizability of the method.
SAND: Smooth Imputation#
The heading “SAND: Smooth Imputation” suggests a novel method for handling missing data in functional data analysis. The name itself implies smoothness as a key feature, addressing a common challenge in functional data where noisy or sparse observations can lead to irregular, jagged imputed curves. The method likely uses self-attention mechanisms, potentially augmented with derivative information, to encourage smoothness during the imputation process. This contrasts with traditional statistical methods which may not explicitly enforce smoothness. Theoretical guarantees on smoothness and error bounds are likely provided, demonstrating the method’s robustness and efficiency. The use of transformer networks suggests the capability to handle irregularly-spaced data, a significant advantage over techniques restricted to regularly sampled data. The approach likely incorporates a deep learning architecture making it suitable for complex data patterns and potentially outperforming traditional methods, especially in the presence of high noise and sparse data.
Theoretical Guarantees#
A theoretical analysis of the proposed method is crucial for establishing its reliability and providing insights into its behavior. Theorem 1 proves the continuous differentiability of imputations, a key property for smooth and accurate results. Theorem 2 connects the number of hidden nodes in the neural network to the prediction error, offering a practical guide for model complexity. These theorems show the method’s effectiveness and the trade-off between accuracy and model size. The theoretical guarantees highlight the robustness and efficiency of the proposed method. Moreover, the analysis reveals a connection to standard dimension-reduction techniques, showcasing its grounding in established statistical methods. While the proofs are provided separately, a high-level understanding of the assumptions and implications of these theorems is essential for a complete evaluation. The theoretical framework enhances the paper’s significance by extending beyond empirical observations and establishing a solid mathematical foundation for the proposed approach.
Real Data Experiments#
In evaluating the efficacy of the proposed SAND method, the research delves into real-world datasets. This is crucial as it demonstrates the method’s ability to handle the complexities and idiosyncrasies of real data beyond simulated scenarios. The selection of datasets is key; choosing datasets that reflect diverse characteristics of functional data, including varying levels of sparsity and noise, strengthens the evaluation. The results from the real data experiments would ideally show SAND’s superior performance compared to existing methods, particularly for challenging datasets with high sparsity or noise. Detailed descriptions of the preprocessing steps for each dataset are crucial for reproducibility. The metrics used to evaluate the performance must align with the aims of the study, perhaps emphasizing smoothness and accuracy of imputation. Ultimately, the real-world results section would validate the method’s practical applicability and demonstrate its potential impact on real-world functional data analysis.
Future Works#
Future research directions stemming from this work on smooth imputation of sparse and noisy functional data using transformer networks could involve several key areas. Extending SAND to handle multivariate functional data would significantly broaden its applicability. Investigating alternative attention mechanisms within the SAND framework, such as those incorporating inductive biases beyond smoothness, warrants exploration. Theoretical analysis could delve deeper into the impact of data characteristics, such as noise distribution and sampling frequency, on the performance of SAND. Furthermore, empirical evaluations on diverse datasets across various domains are needed to fully assess SAND’s robustness and generalizability. Finally, the development of efficient inference techniques for SAND is crucial for its scalability and applicability to large-scale functional data problems.
More visual insights#
More on tables
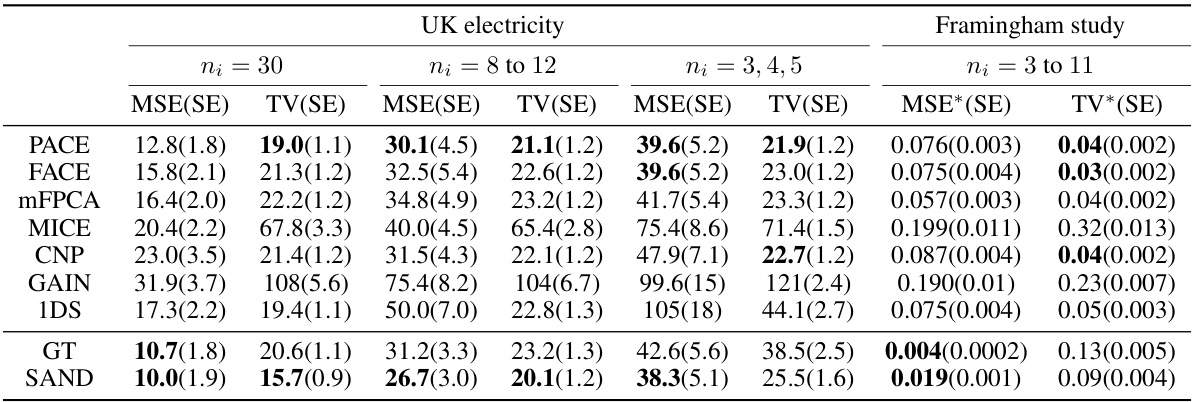
🔼 This table presents the Mean Squared Error (MSE) and Total Variation (TV) along with their standard errors (SE) for different imputation methods on simulated datasets. The data was simulated under various conditions, including different numbers of time points per subject (ni) and noise levels. The bold values highlight the two best-performing methods for each scenario. The MSE measures the average squared difference between the imputed and true values, while the TV measures the total variation in the difference between the imputed and true curves. This table helps to evaluate the performance of various methods under different simulation settings and identifies superior performers for specific scenarios.
read the caption
Table 1: MSE(SE) & TV(SE) on simulated data. Bold values indicate the top 2 performing methods.

🔼 This table presents the Mean Squared Error (MSE) and its standard error (SE) for downstream prediction tasks using different imputation methods. The tasks involve predicting average energy consumption and BMI based on imputed trajectories. The table compares the performance of SAND against PACE, FACE, and GT, highlighting SAND’s superior performance across all prediction tasks and its ability to consistently achieve the lowest MSE. The bold font indicates the lowest MSE for each task.
read the caption
Table 3: MSE(SE) on downstream tasks. Bold font marks the smallest MSE across methods.
Full paper#


















