TL;DR#
Diffusion MRI (dMRI) deconvolution is crucial for understanding brain microstructure, but existing methods are computationally expensive and struggle with limited clinical resolutions. Current deep learning approaches often rely on full-sphere computations and are hampered by high computational demands, especially when dealing with higher angular resolutions. Furthermore, many methods depend on supervised training and/or large ground-truth datasets, limiting their applicability and generalizability.
This paper introduces a novel spatio-hemispherical deconvolution (SHD) method that leverages the antipodal symmetry of neuronal fibers to significantly reduce computational costs. The proposed SHD method uses hemispherical sampling, efficient graph convolutions, and pre-computed Chebyshev polynomials. This approach achieves state-of-the-art results in deconvolution accuracy while offering substantial performance gains over existing methods. It also demonstrates improved robustness to low-angular resolution scans commonly encountered in clinical settings, showcasing its potential for practical applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in diffusion MRI and deep learning. It offers significant efficiency gains in dMRI deconvolution, making high-resolution analysis more practical. The proposed method’s robustness to lower-resolution data also addresses a key challenge in clinical applications, while its unsupervised nature reduces reliance on ground truth data, opening new avenues for future research in high-dimensional spatio-spherical data processing.
Visual Insights#

🔼 This figure shows an example of diffusion MRI (dMRI) and T1-weighted MRI (T1w MRI) data from a single subject in the Human Connectome Project (HCP) dataset. The dMRI data is shown across three different gradient directions, demonstrating the change in signal intensity based on the direction of water diffusion. The inset shows a visualization of the spatio-spherical diffusion signal from a specific region of interest, highlighting the complex patterns of diffusion caused by crossing white matter fibers and the transition between grey and white matter tissue.
read the caption
Figure 1: A diffusion MRI (columns 1–3) and a T1w MRI (column 5) derived from a subject in the HCP Young Adult dataset [70]. The inset (column 4) visualizes a region’s spatio-spherical diffusion signal (b – 1000mm/s²), highlighting crossing-fiber patterns and the grey/white matter interface.
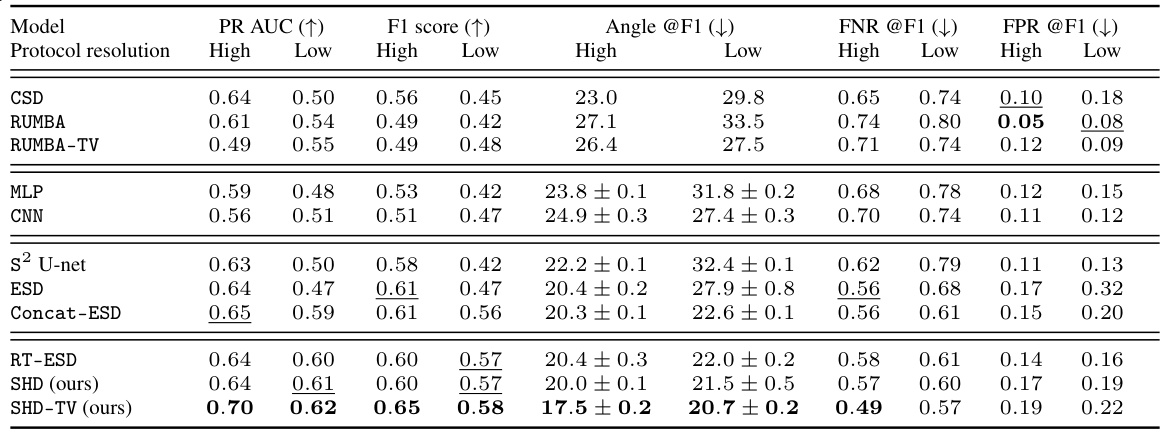
🔼 This table presents the results of fiber detection performance evaluation on the DiSCo dataset for various models, including both conventional and deep learning-based methods. It compares performance at high and low angular resolutions, showing metrics such as PR AUC, F1 score, angular error, FNR, and FPR. Confidence intervals are included where applicable. The models were trained on one volume, validated on another, and tested on a third.
read the caption
Table 1: DiSCo fiber detection performances @ noise level SNR=30 on high and low-resolution data. Models requiring training are trained on the first volume, validated on the second, and tested on the third. Results average over 5 random initialized models. Confidence interval at 95% given if CI is greater than 0.01.
In-depth insights#
Equivariant Convolutions#
Equivariant convolutions are a powerful tool for processing data with inherent symmetries, such as images or 3D shapes. Traditional convolutions lose this symmetry information during the convolution process. Equivariant convolutions, on the other hand, maintain this symmetry by ensuring that if the input is transformed, the output is transformed in a consistent manner. This is particularly useful in domains like medical image analysis (e.g., diffusion MRI) and computer vision where the underlying structure has inherent symmetries (rotations, translations). The key benefit is that this approach requires less data to train effective models. Furthermore, it can improve model performance and generalizability when applied to datasets containing a wide range of transformations. The main challenge is that implementing equivariant convolutions can be computationally more expensive than traditional convolutions, although recent advancements in efficient algorithms address this issue.
SHD Network#
The SHD (Spatio-Hemispherical Deconvolution) Network is a novel deep learning architecture designed for efficient and accurate diffusion MRI (dMRI) deconvolution. It leverages the antipodal symmetry of neuronal fibers, employing hemispherical graph convolutions instead of full spherical ones, resulting in significant computational savings. This approach is coupled with optimized implementations and pre-computed Chebyshev polynomials to further enhance computational efficiency. The network incorporates spatial regularization through a total variation loss, improving the spatial coherence of the recovered fiber orientation distribution functions (fODFs). Experimentally, SHD demonstrates state-of-the-art performance, outperforming existing methods in both speed and accuracy, particularly on clinically-relevant low-angular resolution data. This efficiency allows for training on large datasets, enabling amortized inference, a significant advance over previous subject-specific approaches.
Efficiency Gains#
The research paper highlights significant efficiency gains achieved through the proposed spatio-hemispherical deconvolution (SHD) method. Key improvements stem from leveraging the antipodal symmetry of neuronal fibers, reducing computational costs associated with full spherical convolutions. By employing hemispherical sampling and optimized graph Laplacian operations, SHD demonstrates substantial speedups compared to existing state-of-the-art methods like RT-ESD. Pre-computed Chebyshev polynomials further enhance efficiency, eliminating redundant calculations during inference. The impact is particularly pronounced at higher angular resolutions, typical of research-grade dMRI, where SHD’s efficiency gains are more substantial, making it more practical for large-scale datasets. The study quantifies these gains, showcasing reduced runtime and GPU memory usage, rendering the method suitable for wider clinical applications.
fODF Recovery#
The recovery of fiber orientation distribution functions (fODFs) from diffusion MRI (dMRI) data is a crucial yet challenging task. The ill-posed nature of the inverse problem, compounded by noise and limited angular resolution in clinical scans, necessitates robust and efficient methods. Traditional iterative methods like constrained spherical deconvolution (CSD) often struggle with resolving crossing fibers and are computationally intensive. Deep learning approaches offer a promising alternative, leveraging the power of neural networks to learn complex relationships in spatio-spherical dMRI data. However, achieving high accuracy and efficiency requires addressing the inherent symmetries and geometrical properties of dMRI data. Equivariant neural networks provide a powerful framework by directly incorporating these symmetries in their architecture. Recent advances focus on developing computationally efficient equivariant networks, such as spatio-hemispherical networks, to address the limitations of full spherical convolution. These advancements enable superior fODF recovery, especially in challenging scenarios with crossing fibers and low angular resolution, paving the way for more clinically viable and accurate dMRI analysis.
Future Work#
The authors acknowledge limitations and suggest several promising avenues for future research. Extending the spatio-hemispherical convolution layers to other dMRI tasks, such as denoising and segmentation, is a natural next step, leveraging the model’s inherent efficiency. Further investigation into the robustness of the approach to clinical challenges like subject motion and imaging artifacts is crucial for real-world applicability. Addressing the limitations of undersampled reconstruction, such as fiber hallucination, necessitates exploring more sophisticated regularization strategies. Expanding the applications to other spatio-spherical domains beyond neuroimaging, including robotics and molecular dynamics, is another promising area. Finally, relaxing the assumption of antipodal symmetry in the fODF would broaden the applicability of the methodology to diverse data modalities.
More visual insights#
More on figures
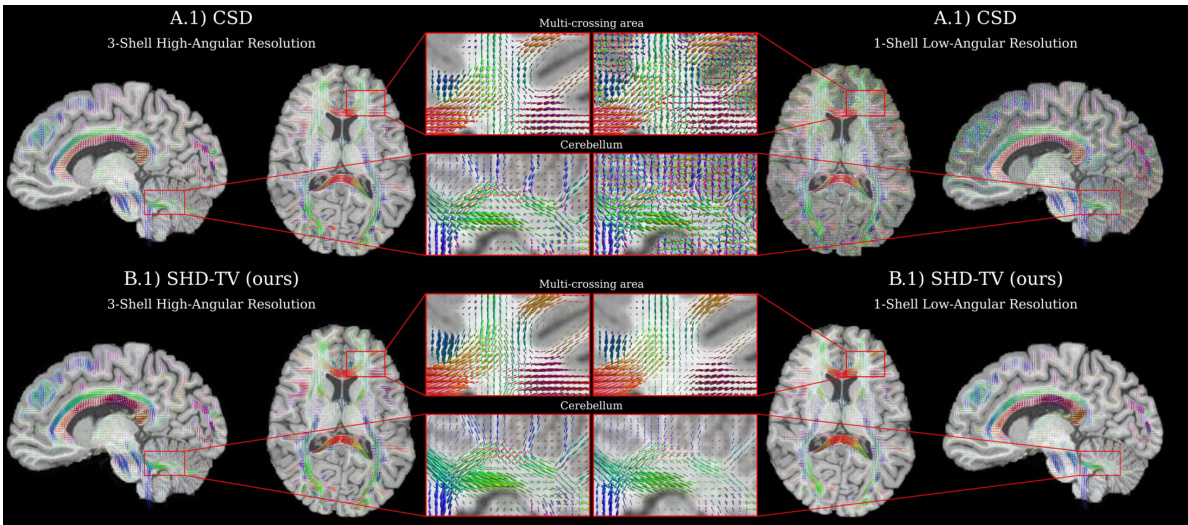
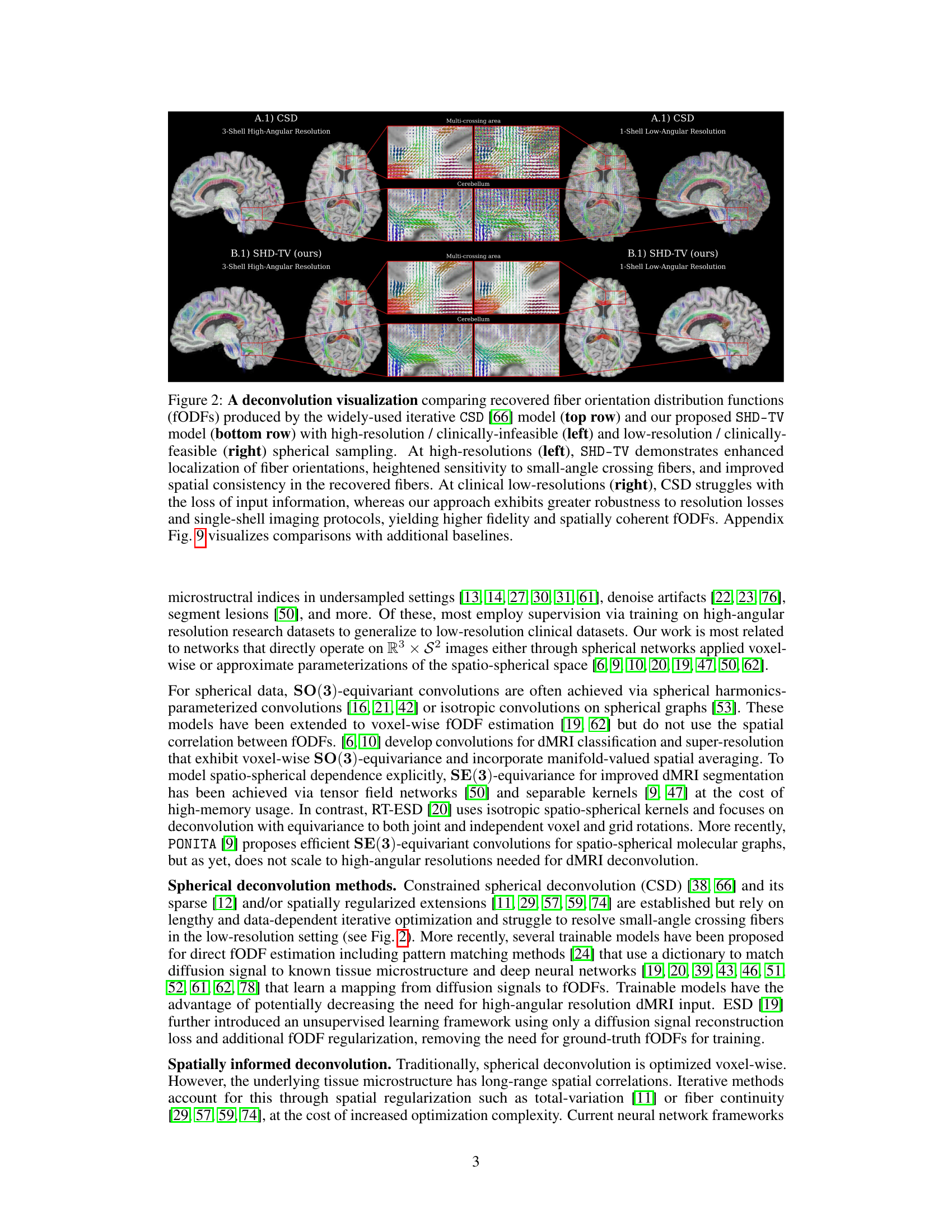
🔼 This figure compares the fiber orientation distribution functions (fODFs) recovered by CSD and SHD-TV at both high and low angular resolutions. It highlights SHD-TV’s improved accuracy and robustness to low resolution data, especially in areas with crossing fibers.
read the caption
Figure 2: A deconvolution visualization comparing recovered fiber orientation distribution functions (fODFs) produced by the widely-used iterative CSD [66] model (top row) and our proposed SHD-TV model (bottom row) with high-resolution / clinically-infeasible (left) and low-resolution / clinically-feasible (right) spherical sampling. At high-resolutions (left), SHD-TV demonstrates enhanced localization of fiber orientations, heightened sensitivity to small-angle crossing fibers, and improved spatial consistency in the recovered fibers. At clinical low-resolutions (right), CSD struggles with the loss of input information, whereas our approach exhibits greater robustness to resolution losses and single-shell imaging protocols, yielding higher fidelity and spatially coherent fODFs. Appendix Fig. 9 visualizes comparisons with additional baselines.
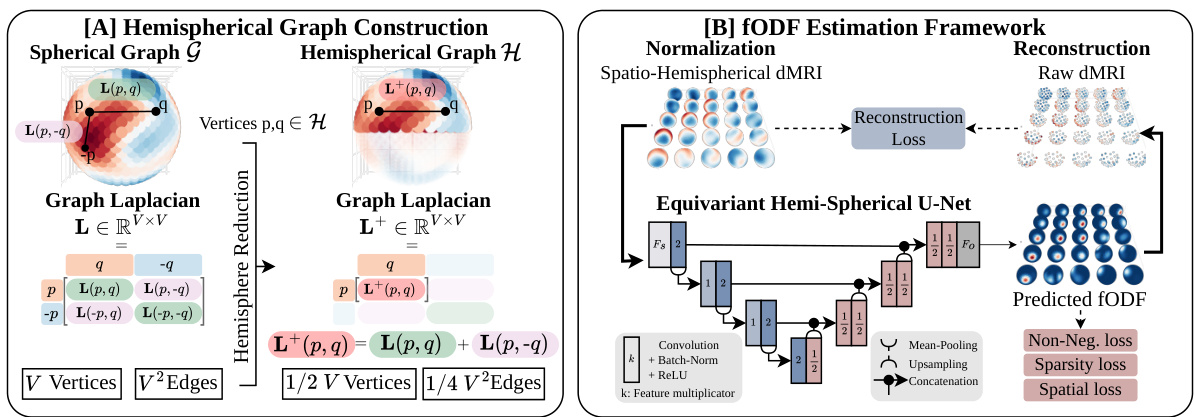
🔼 This figure illustrates the main contributions of the SHD model. (A) shows how the spherical graph is reduced to a hemispherical graph to reduce computational cost. The hemispherical graph preserves the antipodal symmetry of the fODF, while reducing the number of vertices and edges. (B) shows the SHD deconvolution framework. The framework uses the hemispherical graph convolutions to process the spatio-spherical data. This is followed by an equivariant hemispherical U-Net, which is composed of a series of convolutional and upsampling layers. The network is trained using reconstruction loss, non-negativity loss, and sparsity loss. The output of the network is the estimated fODF, which is then used to perform fiber tractography.
read the caption
Figure 3: Contribution overview. A. We reduce the spherical graph (G, L) to an hemispherical graph (H, L+). B. The SHD deconvolution framework operates on a grid of spherical signals and reduces computation complexity while improving neuronal fiber deconvolution.
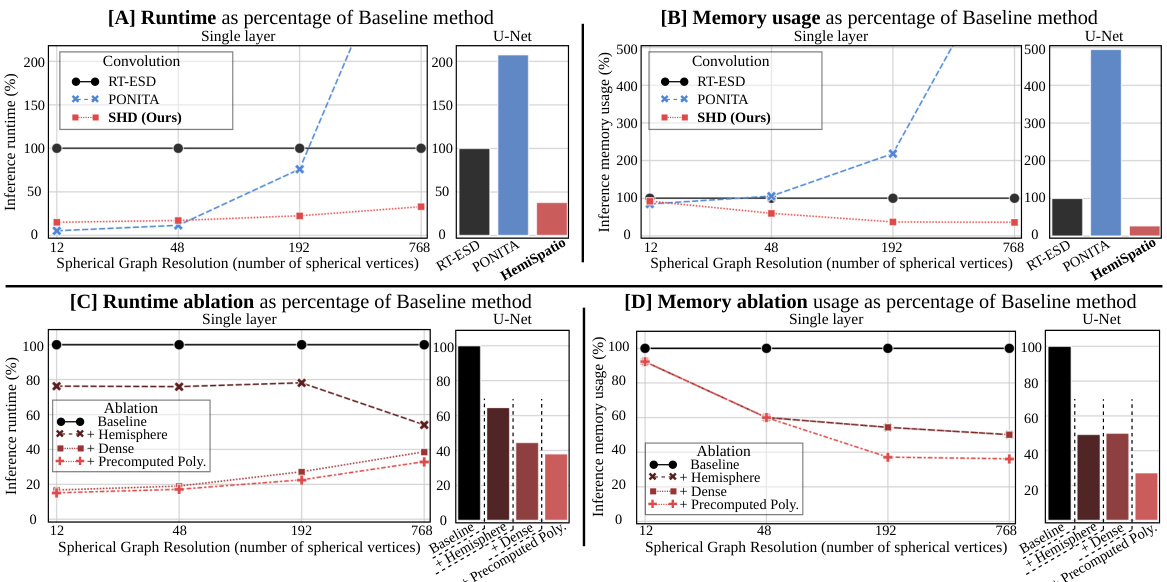
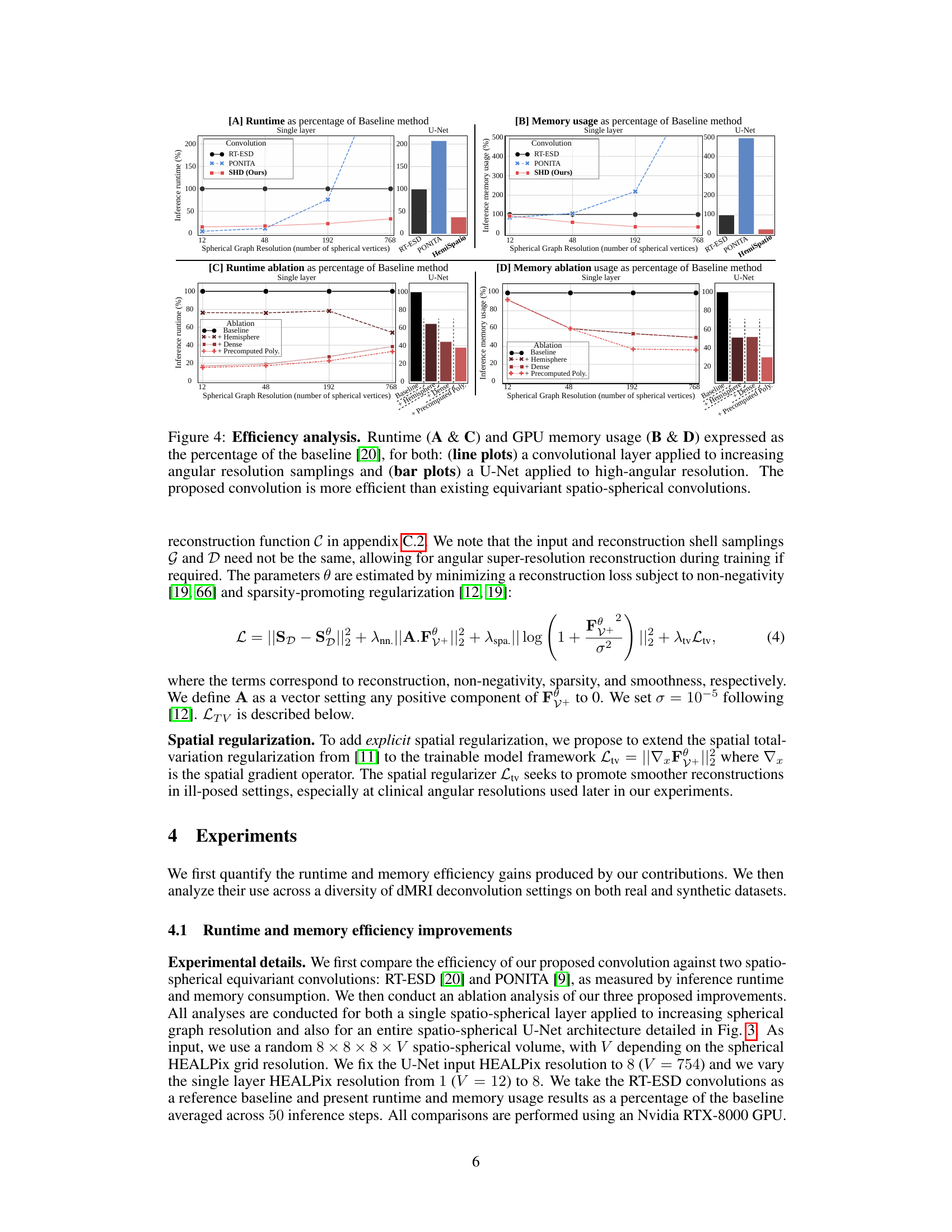
🔼 This figure demonstrates the efficiency gains achieved by the proposed spatio-hemispherical convolution method compared to existing methods. It shows runtime and GPU memory usage as percentages of a baseline method, for both single-layer convolutions and a U-Net architecture. The results indicate significant improvements in efficiency, especially at higher angular resolutions, highlighting the advantages of the proposed approach.
read the caption
Figure 4: Efficiency analysis. Runtime (A & C) and GPU memory usage (B & D) expressed as the percentage of the baseline [20], for both: (line plots) a convolutional layer applied to increasing angular resolution samplings and (bar plots) a U-Net applied to high-angular resolution. The proposed convolution is more efficient than existing equivariant spatio-spherical convolutions.
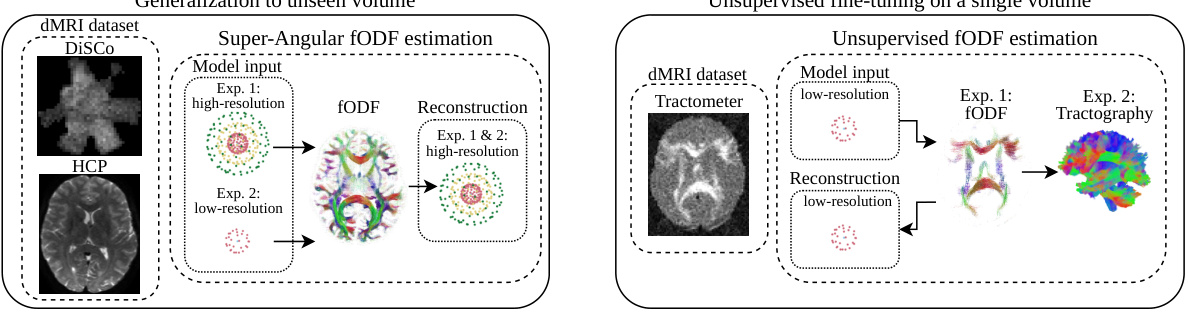
🔼 This figure provides a high-level overview of the experimental setup used in Section 4.2 of the paper. It illustrates the two main types of experiments conducted: (A) Super-resolved fODF estimation on high- and low-angular resolution data using DiSCo and HCP datasets; and (B) Unsupervised fODF estimation and tractography on low-angular resolution data using the Tractometer dataset. The figure helps visualize the different experimental settings and the data used in each.
read the caption
Figure 5: Overview of the diffusion MRI experiments in Section 4.2. [A] We perform super-resolved fODF estimation experiments on two datasets, DiSCo and HCP, respectively. Here, we study the impact of using either high-angular or low-angular resolution as input. [B] We perform quantitative fODF and tractography estimation experiments on Tractometer. We extract fODFs and tractograms from the dMRI with both input and output having low-angular resolution.
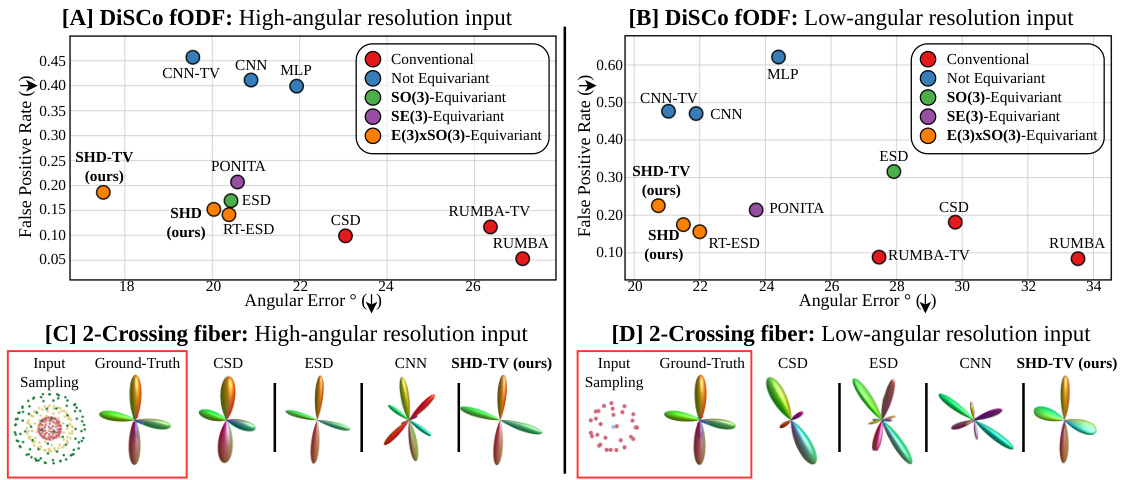
🔼 This figure compares the performance of different fiber detection methods (CSD, ESD, CNN, SHD, SHD-TV, PONITA, RUMBA, RUMBA-TV) on high and low angular resolution inputs of the DiSCo dataset. It shows that the proposed SHD-TV method achieves better results, particularly in the low angular resolution scenario.
read the caption
Figure 6: DiSCo fiber detection performances on high (left col.) and low (right col.) angular resolutions. We first present fODF estimation results on high-angular [A] and low-angular resolution [B] input (closer to bottom-left is better). [C-D] then present a qualitative example of a two-crossing fiber estimation. Our faster implementation SHD does not negatively impact results in comparison to RT-ESD, while our improved model SHD-TV outperforms other methods by providing higher angular precision and less spurious fibers, especially at clinically-viable low-angular resolution.

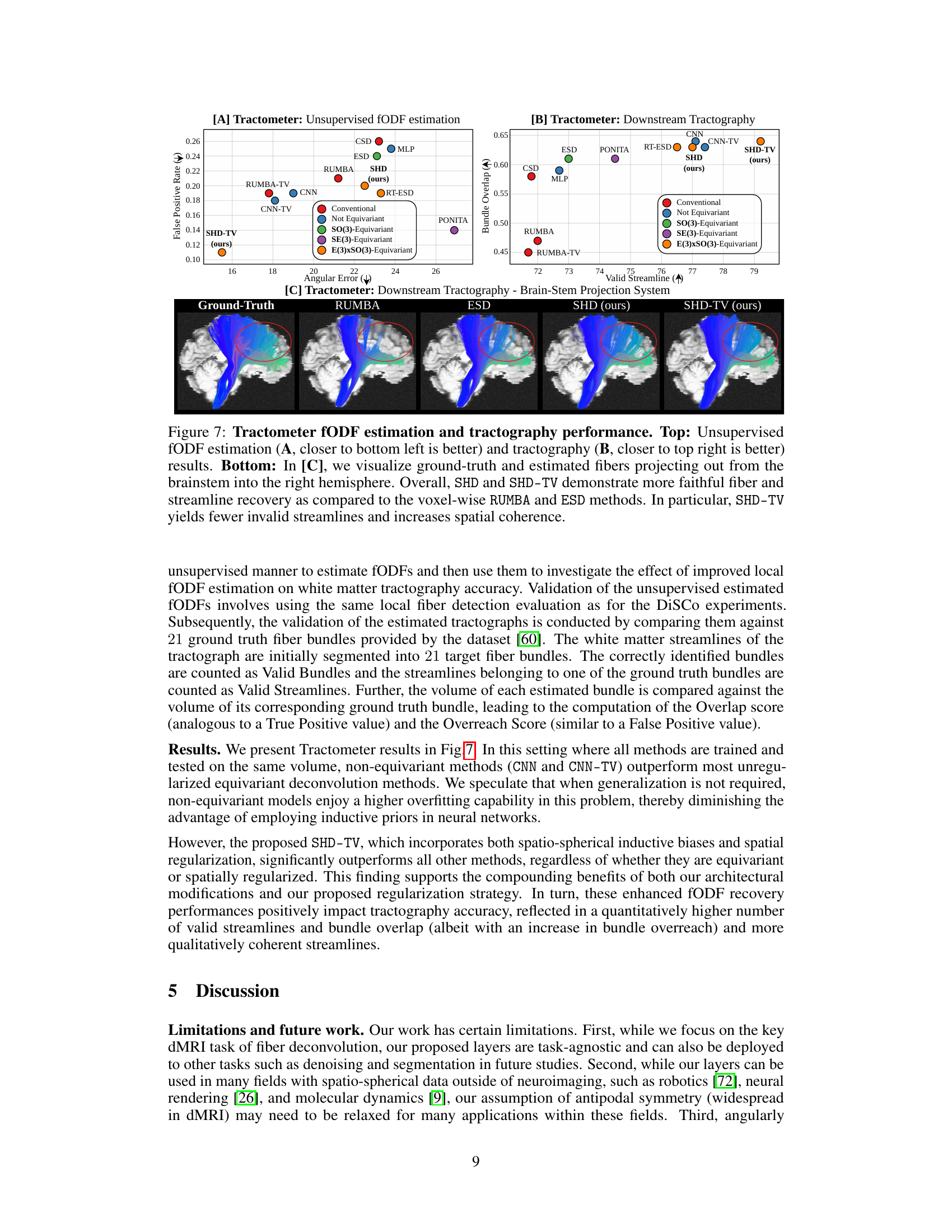
🔼 This figure shows the results of unsupervised fODF estimation and tractography experiments on the Tractometer dataset. The top row displays quantitative results comparing SHD and SHD-TV to other methods for both fODF estimation and tractography. The bottom row shows a qualitative comparison of the fiber pathways estimated by various methods to a ground truth, illustrating the improved accuracy and coherence of SHD and SHD-TV.
read the caption
Figure 7: Tractometer fODF estimation and tractography performance. Top: Unsupervised fODF estimation (A, closer to bottom left is better) and tractography (B, closer to top right is better) results. Bottom: In [C], we visualize ground-truth and estimated fibers projecting out from the brainstem into the right hemisphere. Overall, SHD and SHD-TV demonstrate more faithful fiber and streamline recovery as compared to the voxel-wise RUMBA and ESD methods. In particular, SHD-TV yields fewer invalid streamlines and increases spatial coherence.

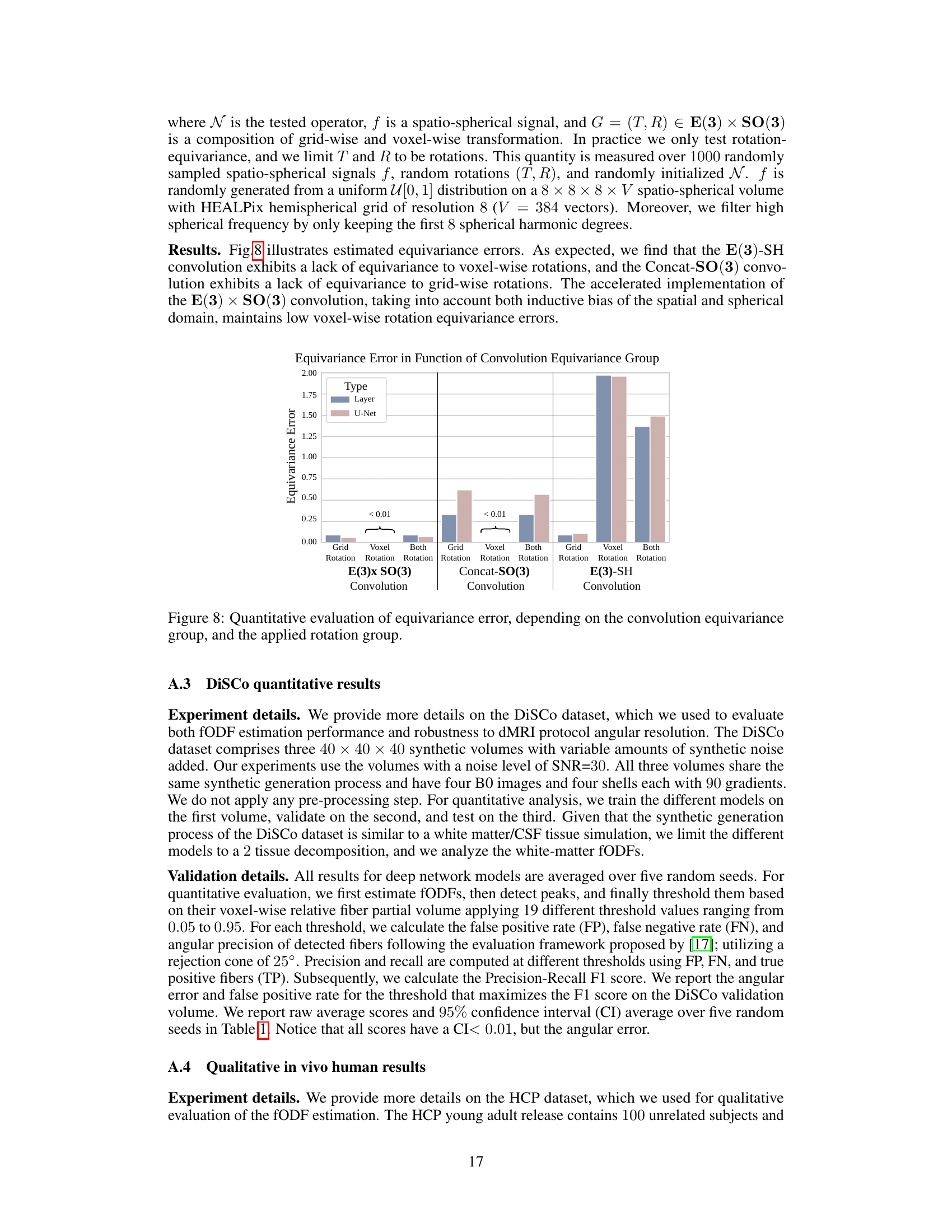
🔼 The figure shows a bar chart comparing the equivariance error of three different convolution methods (E(3)xSO(3), Concat-SO(3), and E(3)-SH) for both single-layer and U-Net architectures. The error is measured under different rotation scenarios (grid rotation, voxel rotation, and both). The results indicate that the E(3)xSO(3) convolution exhibits low equivariance error across all rotation scenarios, demonstrating its robustness and effectiveness.
read the caption
Figure 8: Quantitative evaluation of equivariance error, depending on the convolution equivariance group, and the applied rotation group.

🔼 This figure provides a qualitative comparison of the fiber orientation distribution functions (fODFs) and tractography results obtained using different methods, including the proposed SHD-TV method and several baselines such as CSD and ESD. The comparison is shown for both high-angular and low-angular resolution input data, highlighting the performance differences across various methods under different conditions. The figure visually demonstrates the impact of the proposed method’s enhanced spatial coherence and improved sensitivity in resolving crossing fibers, particularly in low-angular resolution data.
read the caption
Figure 9: Qualitative illustration comparing the proposed equivariant dMRI deconvolution framework against all other baselines.
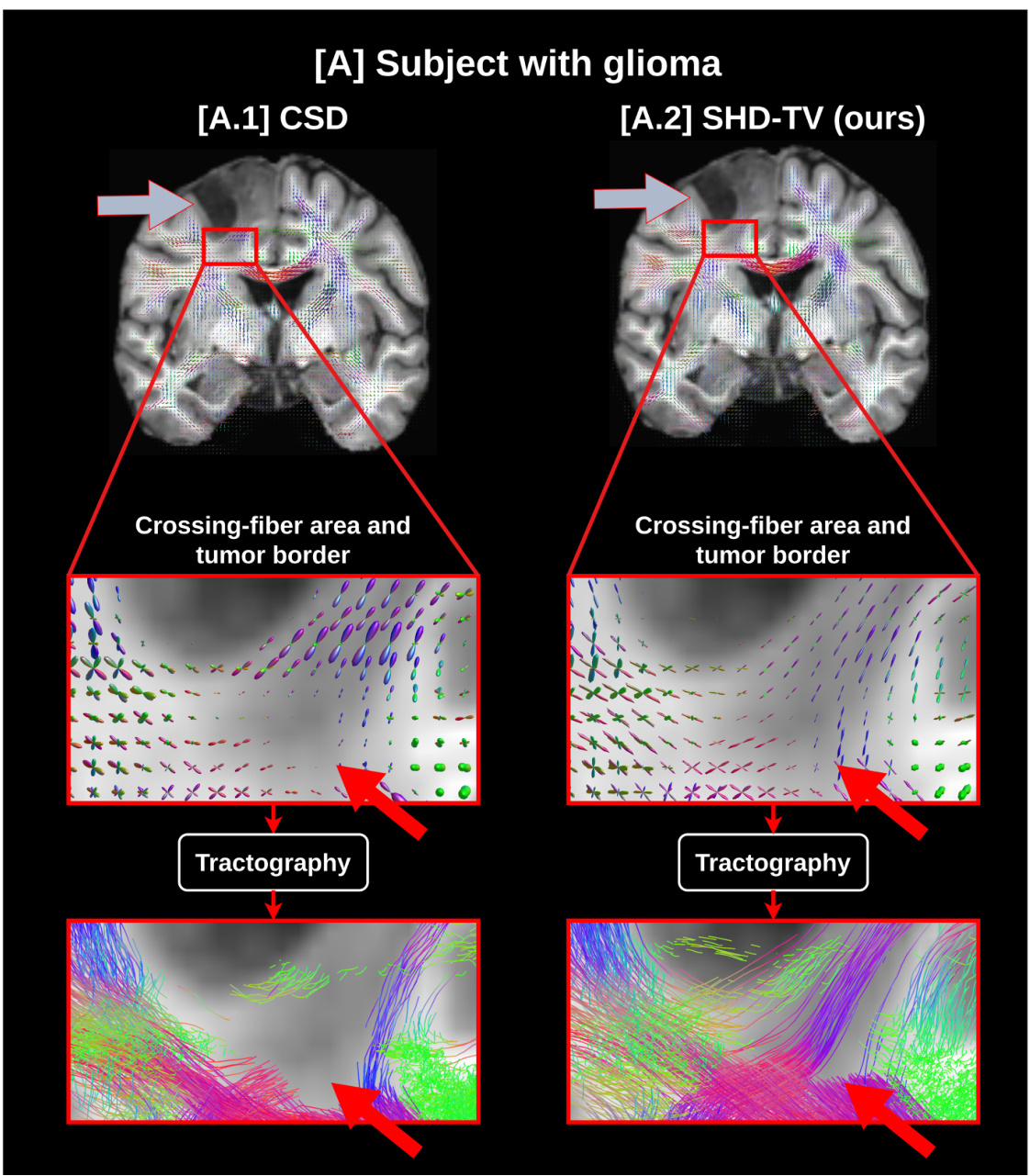
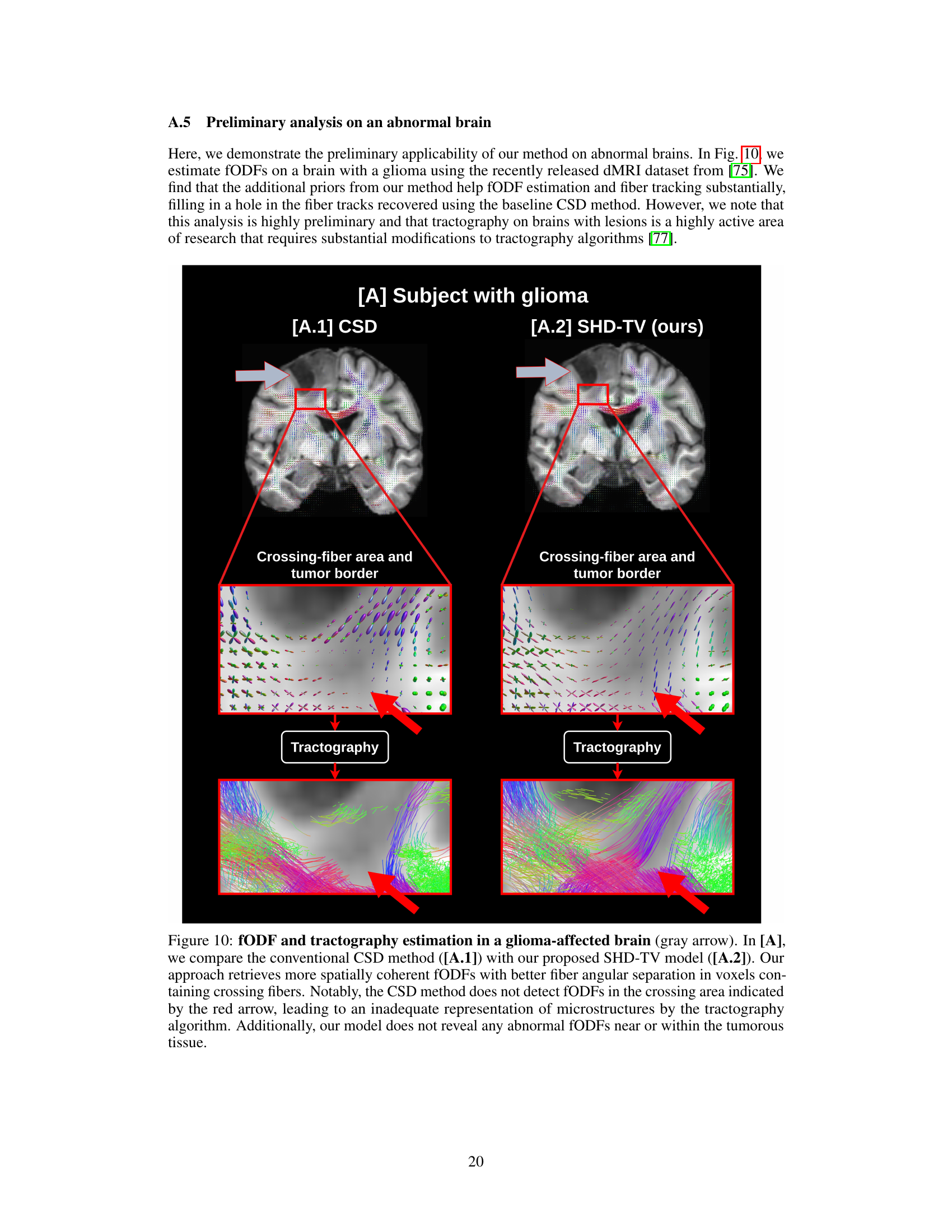
🔼 This figure compares the fiber orientation distribution function (fODF) and tractography results of the conventional CSD method and the proposed SHD-TV method for a brain with a glioma. The SHD-TV method demonstrates improved spatial coherence of fODFs and more accurate fiber tracking, particularly in areas with crossing fibers near the tumor. The CSD method fails to detect fODFs in some crossing fiber areas, resulting in less accurate tractography.
read the caption
Figure 10: fODF and tractography estimation in a glioma-affected brain (gray arrow). In [A], we compare the conventional CSD method ([A.1]) with our proposed SHD-TV model ([A.2]). Our approach retrieves more spatially coherent fODFs with better fiber angular separation in voxels containing crossing fibers. Notably, the CSD method does not detect fODFs in the crossing area indicated by the red arrow, leading to an inadequate representation of microstructures by the tractography algorithm. Additionally, our model does not reveal any abnormal fODFs near or within the tumorous tissue.
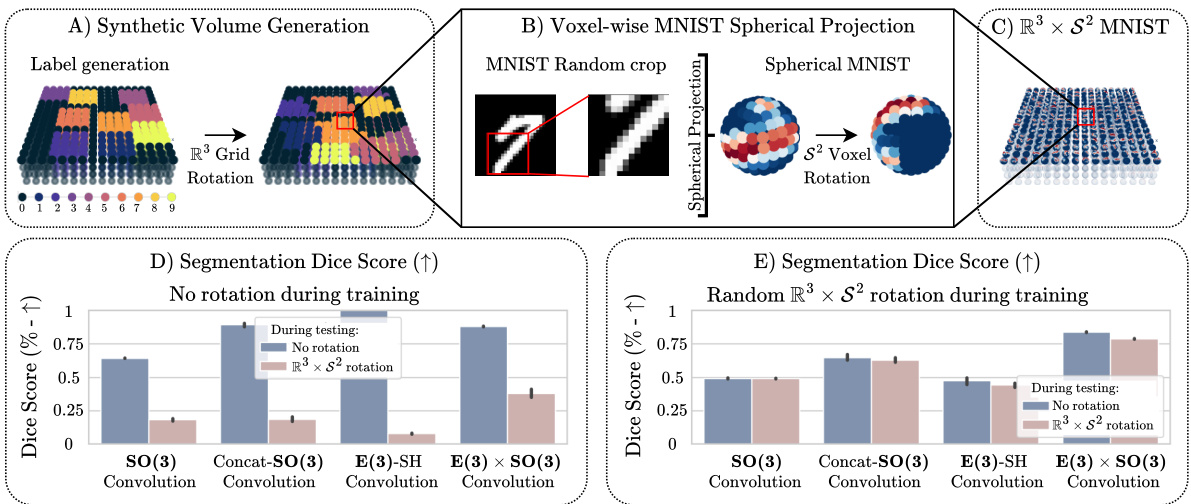
🔼 This figure shows the process of generating synthetic spatio-spherical MNIST data and the results of comparing models with and without data augmentation. The top row illustrates the steps involved in generating the data: synthetic volume generation, voxel-wise MNIST spherical projection, and the final R³ x S² MNIST dataset. The bottom row presents a comparison of the segmentation dice scores for different models trained under various conditions (with and without data augmentation and different types of convolutions). The results demonstrate that the E(3) x SO(3) convolution offers superior generalization capabilities to unseen transformations, and the inclusion of the correct inductive bias improves performance compared to data augmentation alone.
read the caption
Figure 11: Top row: Spatio-Spherical MNIST generation process. Bottom row: Results from testing generalization from equivariance vs. data augmentation on the synthetic R³ × S² MNIST classification task. [A-C] Dataset generation process. [D-E] Segmentation dice score of models trained without (D) and with (E) data augmentation. Overall, our proposed E(3) × SO(3) convolution has a higher generalization power to unseen transformation than its non-equivariant counterparts, and the right inductive bias increases segmentation performance against data augmented-only models.

🔼 This figure illustrates the steps involved in the spatio-hemispherical convolution process. It starts with a 3D grid of hemispherical graphs (A). Then, voxel-wise spherical filtering is performed using a proposed hemispherical Laplacian (B), followed by concatenation of the filtered outputs (C). The result is then processed using 3D isotropic convolution with weight sharing across the hemispherical graph vertices (D, E) producing the final convolution output (F).
read the caption
Figure 12: Overview of the Hemispherical E(3) × SO(3) Convolution computation. This figure is adapted from [20]. [A-C] The input of the convolution is a 3D grid of hemispherical graphs with V vertices per voxel. The input is first processed by voxel-wise spherical filtering using the proposed hemispherical Laplacian and efficient implementation. [D-F] The 3D volume is then processed by a 3D isotropic convolution with weight-sharing across the hemispherical graph vertex.
🔼 This figure shows a comparison of diffusion MRI (dMRI) and T1-weighted MRI (T1w MRI) images from a human subject in the Human Connectome Project (HCP) dataset. The main part of the figure displays three gradient direction dMRI images, representing water diffusion in the brain, where each gradient direction provides the signal from the brain in a specific direction. The T1w MRI image provides anatomical information of the brain structure. In the inset, a spatio-spherical signal representation from a brain region is shown. This representation is a combination of spatial and angular information, showing the diffusion signal in various directions from different spatial locations in the brain. The spatio-spherical signal highlights the crossing patterns of fibers and the interface between gray matter and white matter.
read the caption
Figure 1: A diffusion MRI (columns 1–3) and a T1w MRI (column 5) derived from a subject in the HCP Young Adult dataset [70]. The inset (column 4) visualizes a region’s spatio-spherical diffusion signal (b – 1000mm/s²), highlighting crossing-fiber patterns and the grey/white matter interface.
Full paper#