DDGS-CT: Direction-Disentangled Gaussian Splatting for Realistic Volume Rendering

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents a novel and efficient method for generating realistic X-ray images (DRRs) from CT scans. This is crucial for various medical applications, particularly in image-guided surgery and radiotherapy planning, where real-time or near real-time image generation is essential. The method significantly improves accuracy and efficiency compared to existing approaches, opening up new avenues for research in medical image processing and related fields.

Visual Insights

#

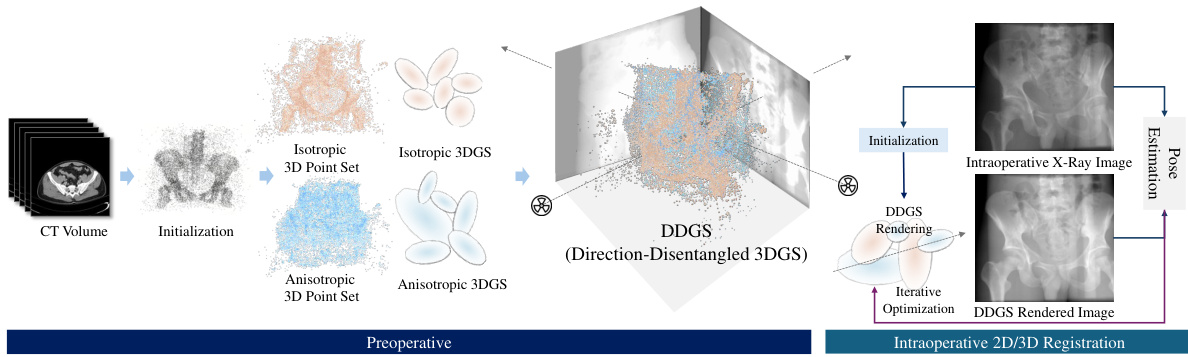
The figure illustrates the DDGS pipeline, which starts with a CT volume and generates a realistic intraoperative X-ray image. The process involves initialization, generating isotropic and anisotropic 3D Gaussian splatting point sets, then uses DDGS rendering to produce the final image. This image is then used for intraoperative 2D/3D registration. This highlights the workflow from pre-operative CT scan data to the final 2D/3D registration step using the DDGS method.

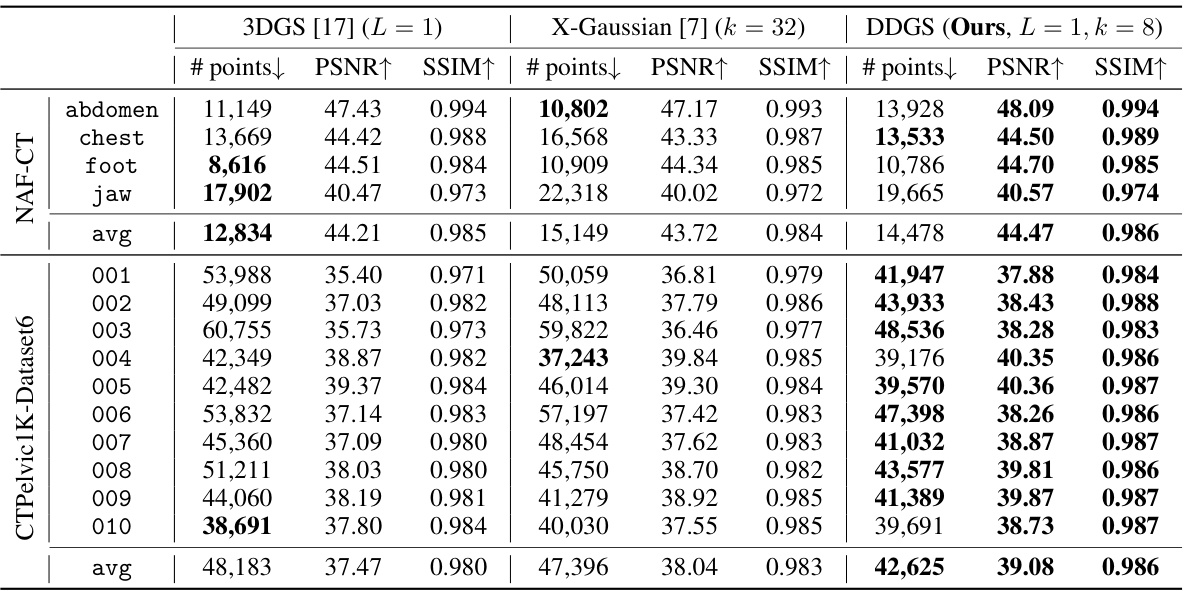
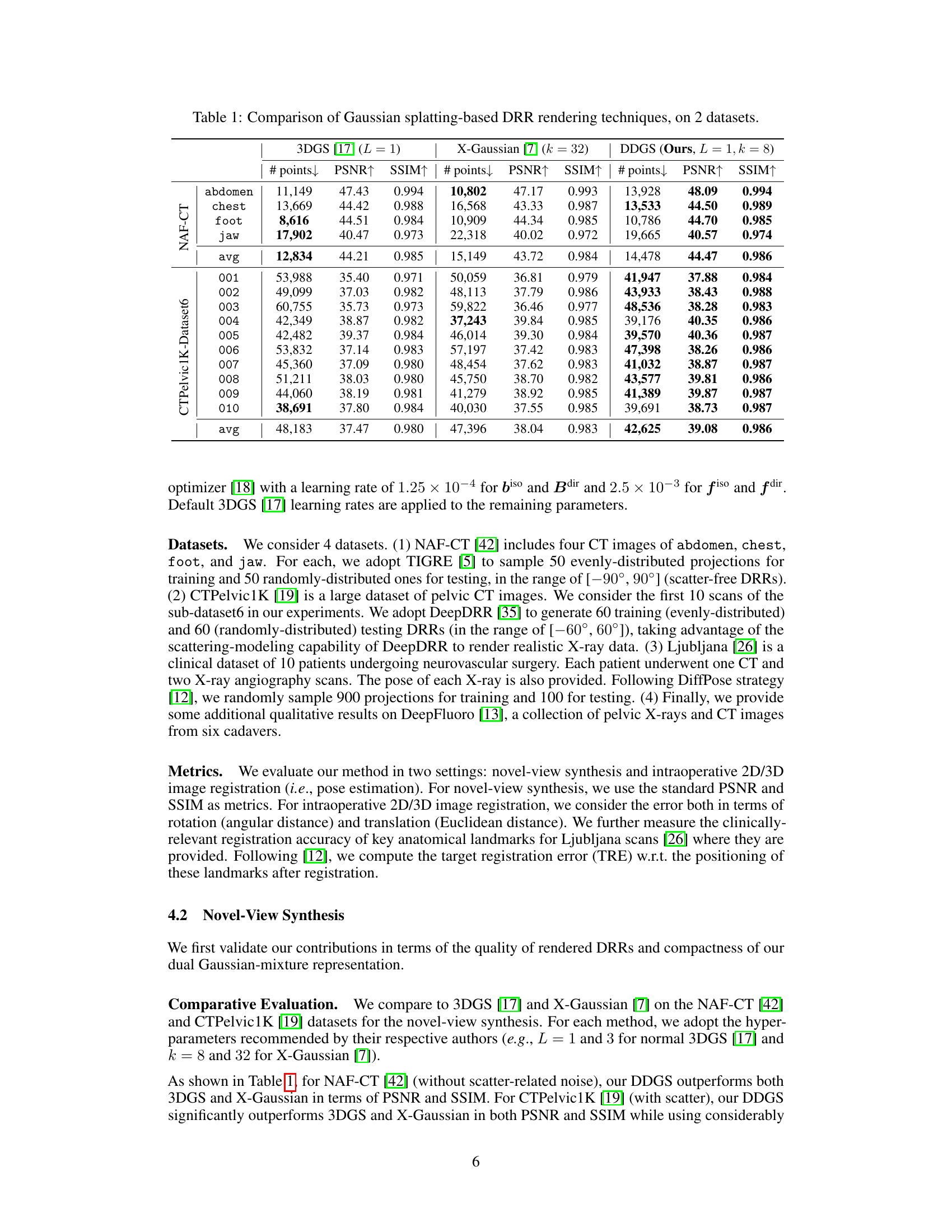
This table compares the performance of three different Gaussian splatting-based methods for digitally reconstructed radiograph (DRR) rendering on two datasets: NAF-CT and CTPelvic1K. The methods compared are 3DGS (a baseline method), X-Gaussian, and the proposed DDGS method. For each method and dataset, the table shows the number of points used in the Gaussian splatting representation, and the resulting peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) values, which are common metrics for evaluating image quality. Higher PSNR and SSIM values indicate better image quality. The table demonstrates that the proposed DDGS method outperforms the other two methods in terms of both PSNR and SSIM on both datasets.

In-depth insights

#

DDGS-CT Overview

#

DDGS-CT, or Direction-Disentangled Gaussian Splatting for Computed Tomography, presents a novel approach to realistic volume rendering. It cleverly combines physics-based X-ray simulation with the efficiency of 3D Gaussian splatting. Unlike previous methods, DDGS-CT addresses anisotropic X-ray interactions, such as Compton scattering, by separating the radiosity contribution into isotropic and direction-dependent components. This allows for a more accurate representation of X-ray image formation without the computational cost of Monte Carlo methods. The method’s adaptive 3DGS initialization, tailored to tomography data properties, further enhances accuracy and speed. DDGS-CT demonstrates superior performance in image accuracy and runtime compared to existing techniques, showcasing its potential for real-time intraoperative applications and inverse problems like pose registration. The disentanglement of isotropic and anisotropic components is a key innovation, allowing for efficient modeling of complex scattering effects. Overall, DDGS-CT offers a significant advancement in realistic volume rendering, bridging the gap between accuracy and efficiency for medical imaging applications.

3DGS Adaptation

#

Adapting 3D Gaussian splatting (3DGS) for realistic volume rendering of X-ray images presents unique challenges. Directly applying standard 3DGS methods is insufficient because they don’t inherently model the physics of X-ray interaction with matter, particularly the anisotropic effects of Compton scattering. A key insight is the decomposition of the radiosity contribution into isotropic and anisotropic components. This allows for modeling isotropic interactions (like photoelectric absorption) with a simpler, efficient approach while approximating complex anisotropic scattering effects without computationally expensive simulations. Adapting the 3DGS initialization is crucial for efficiency and accuracy. A radiodensity-aware dual sampling strategy is proposed to intelligently sample 3D points, focusing on material interfaces and homogeneous regions to improve the representation of complex anatomical structures and achieve a balance between accuracy and model compactness. The combination of disentangling isotropic and anisotropic components and the optimized initialization provides a more accurate and efficient framework for generating realistic X-ray images compared to previous analytical approaches, which often suffer from simplifying assumptions that limit their accuracy.

Radiodensity Init

#

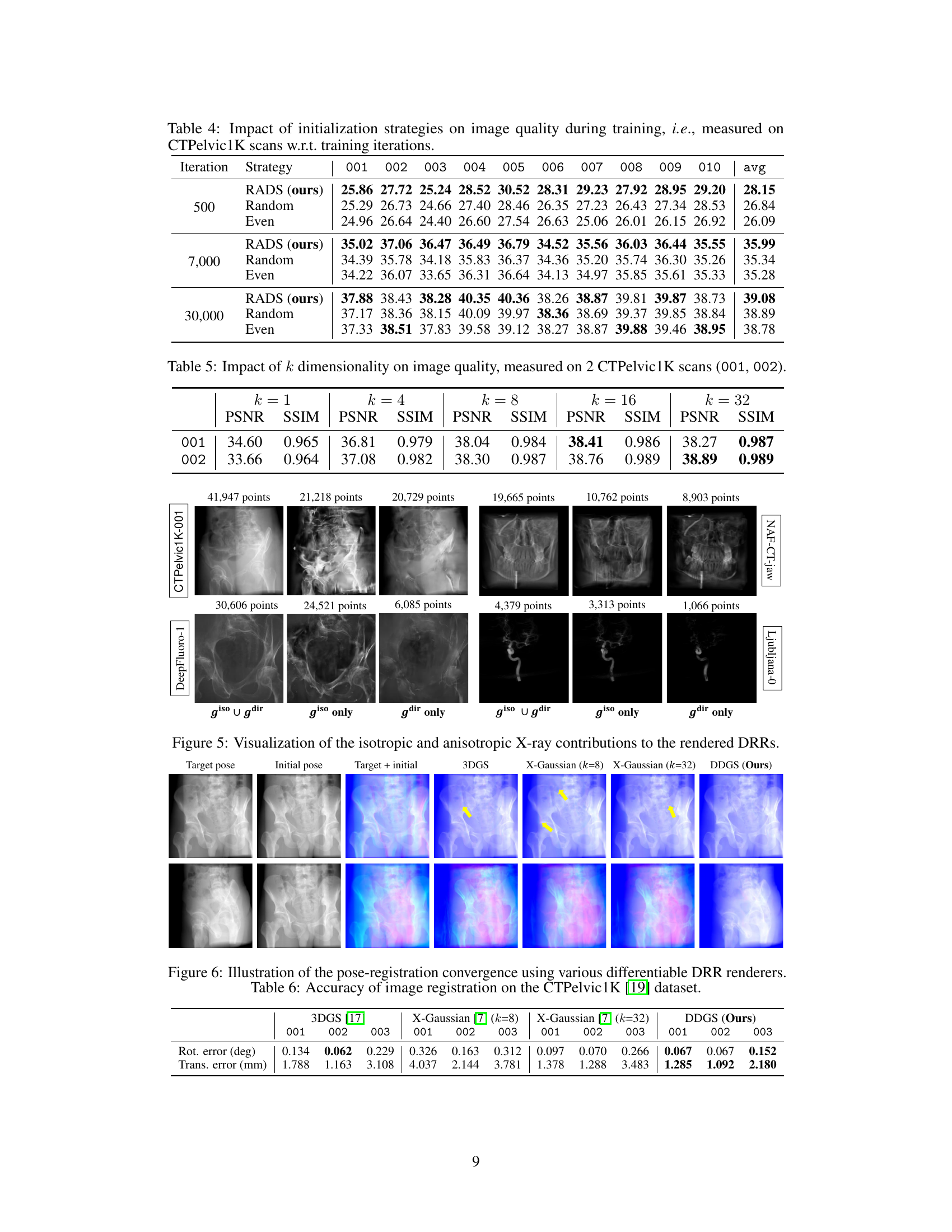
The heading ‘Radiodensity Init’ suggests an initialization strategy in a computational imaging method, likely focusing on how initial conditions for a model are set based on radiodensity. Radiodensity refers to the degree of X-ray attenuation by different tissues, crucial for accurate image reconstruction. This approach likely involves using radiodensity information from a CT scan to intelligently sample points (e.g., using marching cubes to identify material interfaces or density-weighted sampling for homogeneous regions) for model initialization. This is a significant improvement over uniform or random sampling, as it leverages domain expertise to prioritize relevant regions, leading to faster convergence and potentially improved reconstruction accuracy. The use of radiodensity directly incorporates essential physical properties, making the initialization more informed and tailored to the specific task of X-ray imaging. The resulting point cloud would then be used to initialize 3D Gaussian splatting, or a similar representation, better capturing the underlying image formation process. This targeted initialization is key for achieving accurate and efficient volume rendering, particularly in real-time or intraoperative scenarios where computational cost is a major concern.

DRR Accuracy

#

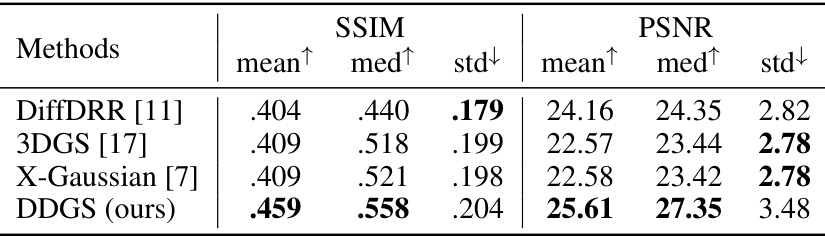
Evaluating the accuracy of Digitally Reconstructed Radiographs (DRRs) is crucial for their effectiveness in medical imaging applications. Several factors influence DRR accuracy, including the fidelity of the input CT data, the accuracy of the underlying X-ray physics model, and the efficiency of the rendering algorithm. Physics-based Monte Carlo methods are considered the gold standard due to their realistic simulation of X-ray interactions, but they are computationally expensive. Analytical methods are faster but often make simplifying assumptions that compromise accuracy, especially regarding anisotropic scattering effects. This paper explores a novel approach that attempts to strike a balance between accuracy and efficiency. The method’s accuracy is thoroughly evaluated using various metrics and benchmarks, comparing it against state-of-the-art techniques. A key focus is on measuring the impact of specific design choices, such as the direction-disentangled Gaussian splatting approach and the radiodensity-aware initialization strategy, on the overall DRR quality. This multifaceted evaluation of DRR accuracy provides valuable insights into the strengths and weaknesses of different methods and guides future development efforts towards more accurate and efficient DRR generation.

Future Work

#

Future research directions stemming from this work could explore several promising avenues. Extending the DDGS model to handle polychromatic X-ray sources would enhance realism, as would incorporating more sophisticated scattering models beyond Compton scattering. Investigating the impact of different CT scan resolutions and noise levels on DDGS performance is crucial for practical applications. The generalizability of DDGS to other imaging modalities such as fluoroscopy and cone-beam CT warrants exploration. Furthermore, developing more efficient training strategies and optimizing the Gaussian splatting initialization could further boost accuracy and speed. Finally, the integration of DDGS into a complete intraoperative workflow would be invaluable, addressing challenges such as real-time pose registration, image guidance, and robust handling of anatomical variations.

More visual insights

#

More on figures

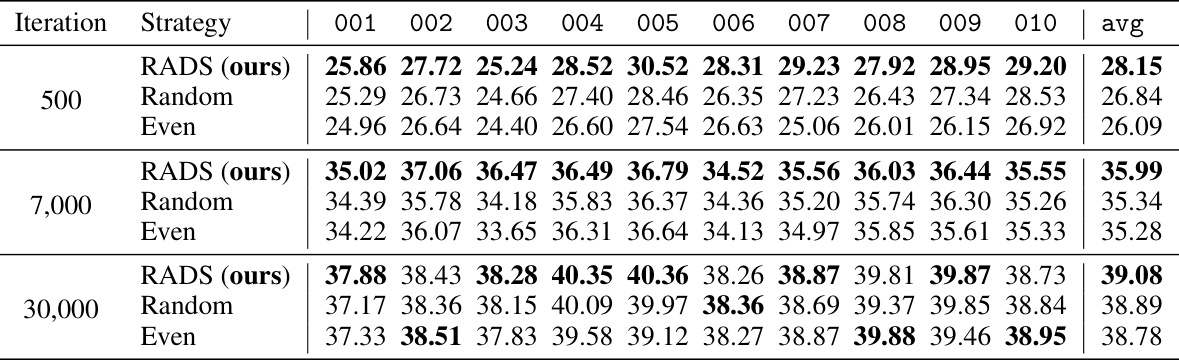
This figure illustrates four different sampling strategies used to initialize the 3D Gaussian splatting (3DGS) representation for X-ray image generation. It compares uniformly random sampling, evenly spaced sampling, marching cubes algorithm-based sampling which focuses on the surfaces between different materials, and a novel radiodensity-aware dual sampling (RADS) method which combines marching cubes and density-weighted sampling. RADS is the proposed method in the paper, aiming for better accuracy and efficiency by considering the properties of tomography data.

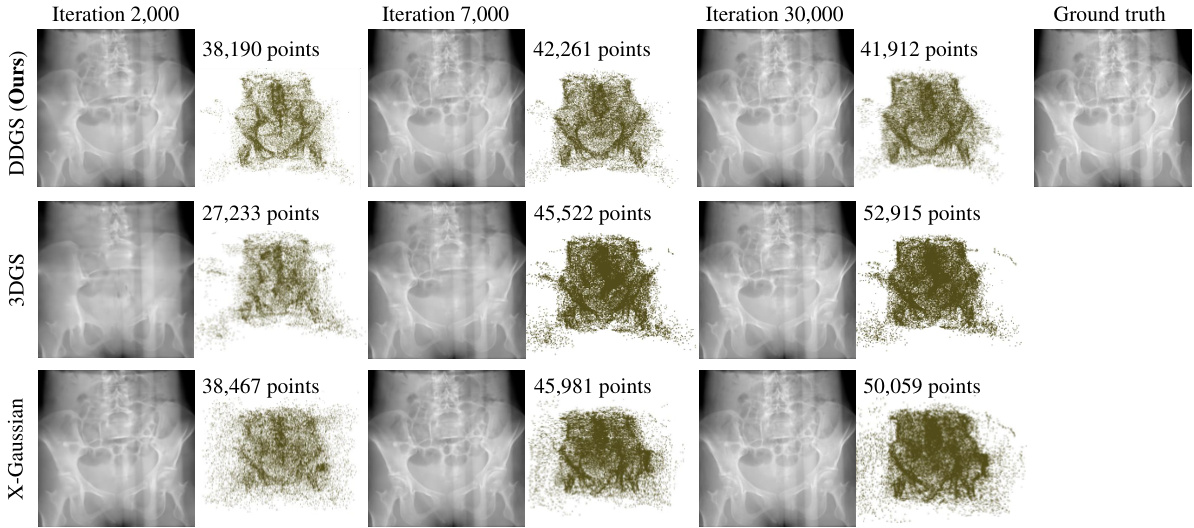
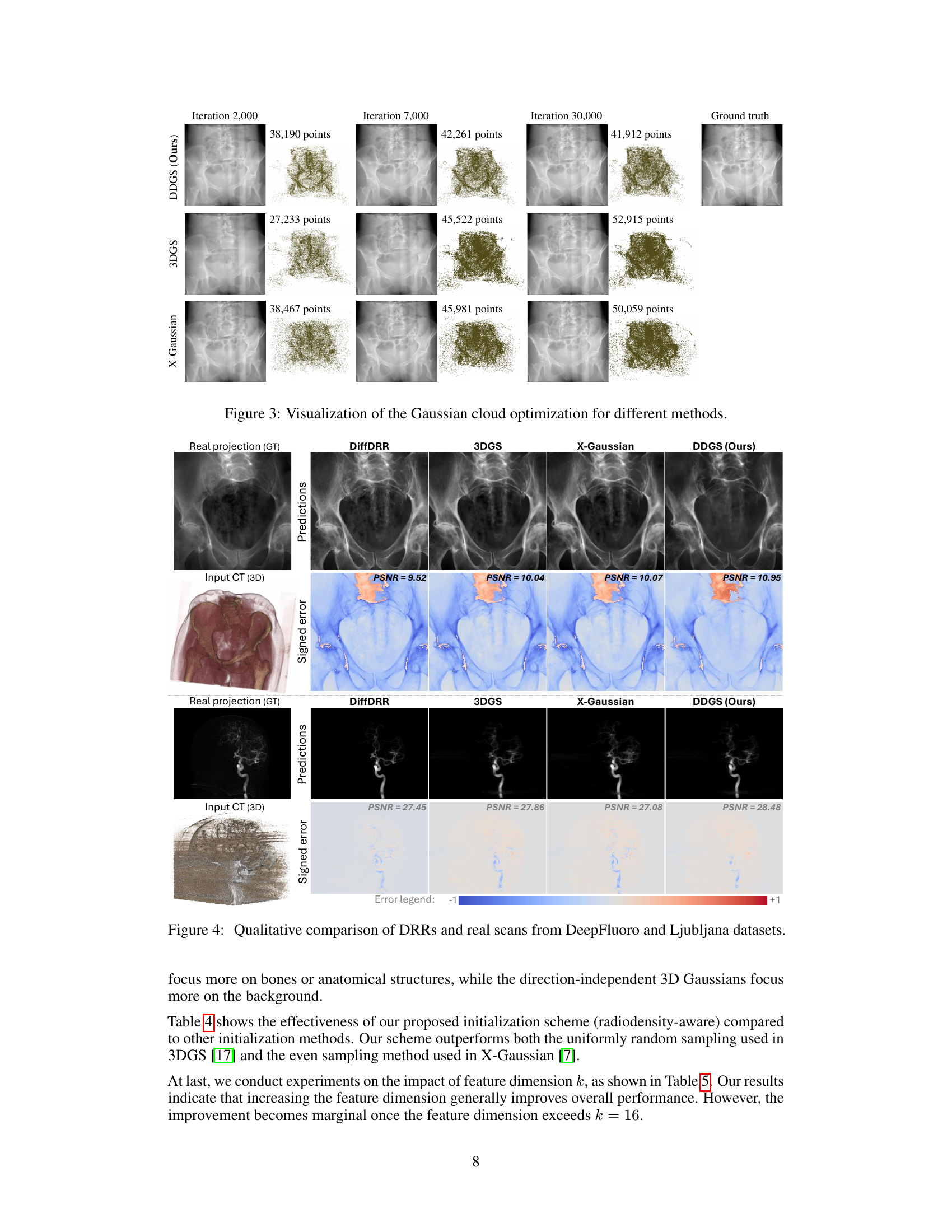
This figure visualizes the Gaussian cloud optimization process for three different methods: DDGS (Ours), 3DGS, and X-Gaussian. It shows the evolution of the Gaussian cloud at three different iterations (2,000, 7,000, and 30,000) alongside the ground truth. The number of points in the Gaussian cloud is also indicated for each iteration and method.

This figure presents a qualitative comparison of Digitally Reconstructed Radiographs (DRRs) generated by different methods against real X-ray scans from two datasets: DeepFluoro and Ljubljana. The top row shows a comparison for pelvic bone structures, while the bottom row shows a comparison for neurovascular structures. Each column represents a different method: DiffDRR, 3DGS, X-Gaussian, and the proposed DDGS method. For each image, the input 3D CT scan, the generated DRR, and a signed error map highlighting the difference between the generated DRR and the real scan are displayed. The PSNR values are provided to quantify the image quality of each method.

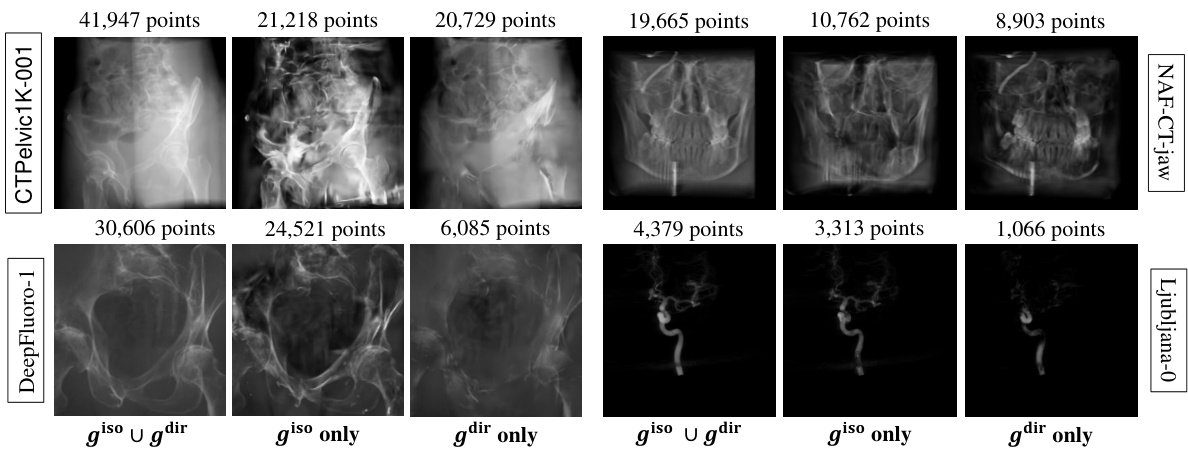
This figure visualizes the Gaussian cloud optimization for different methods across various iterations (2000, 7000, 30000). Each row represents a different dataset (CTPelvic1K, NAF-CT, Ljubljana), showing the distribution of Gaussian points for DDGS (ours), 3DGS, and X-Gaussian at different optimization stages. The ground truth image is also provided for comparison. The number of points used in each optimization is also shown. This helps to understand the evolution of Gaussian splatting during optimization.

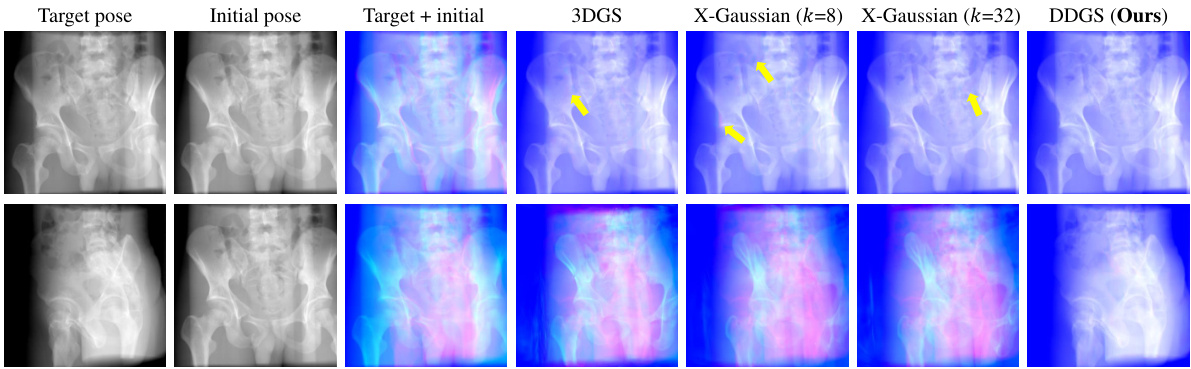
This figure visualizes the Gaussian cloud optimization process for different methods at different iterations. The top row shows the rendered images for each method, while the bottom row presents a visualization of the Gaussian cloud. It allows for a comparison between the Gaussian point cloud distribution learned by the different methods: 3DGS, X-Gaussian, and DDGS, at different optimization stages. This illustrates how each method’s internal representation adapts to the target image data during training. The Ground Truth is included for reference.

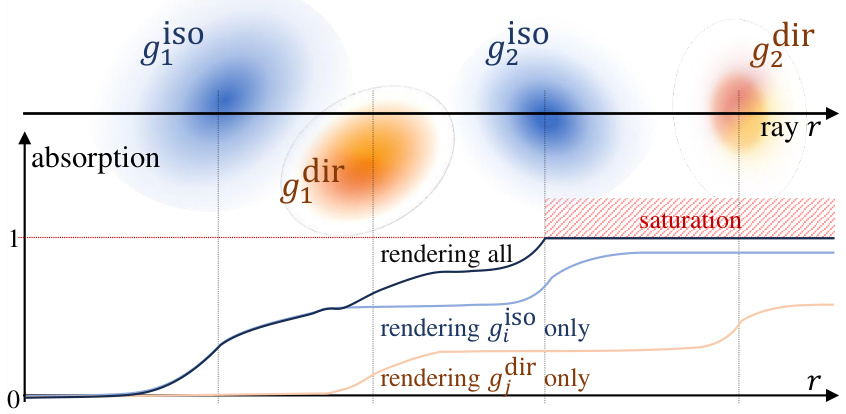
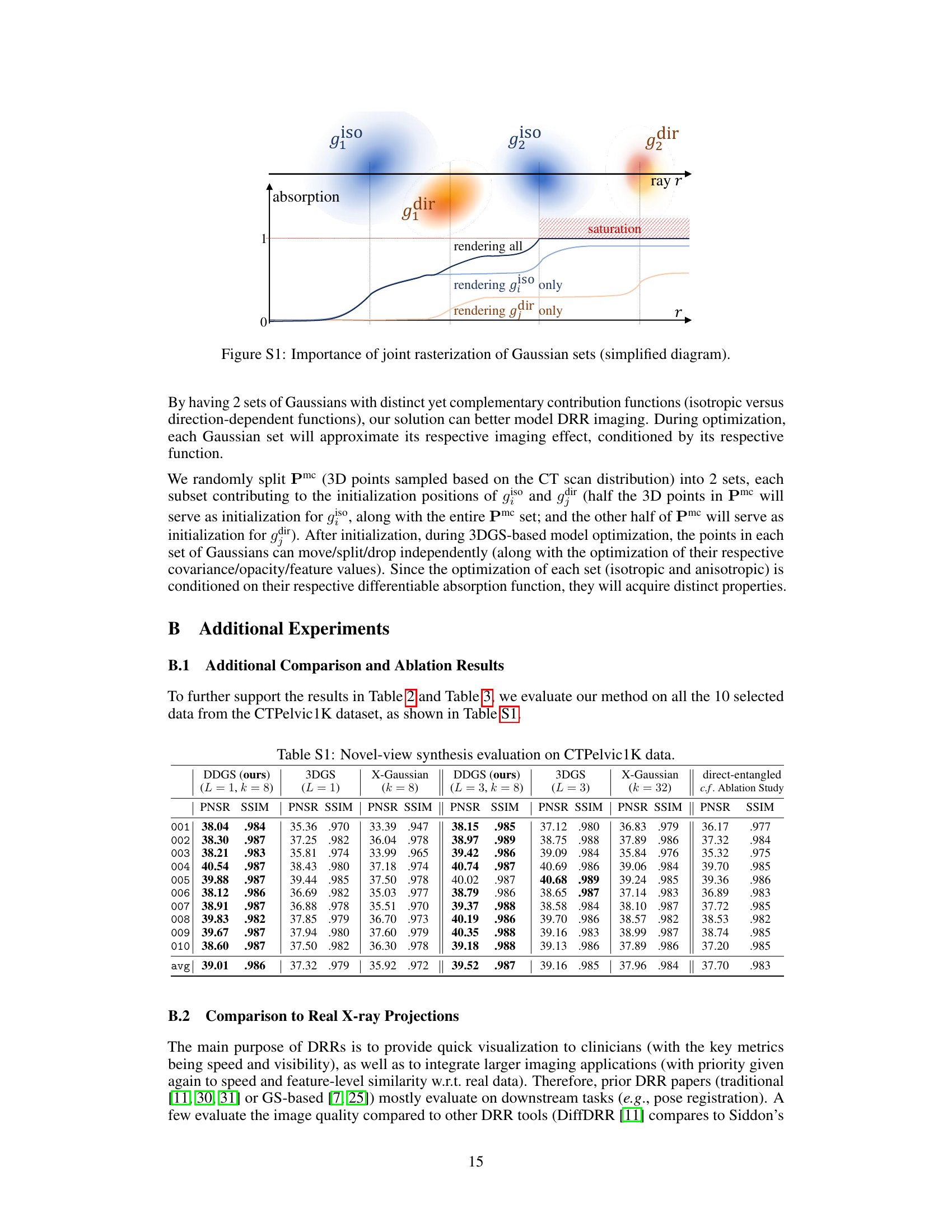
This figure illustrates the importance of jointly rasterizing isotropic and anisotropic Gaussian sets in the proposed DDGS method. It shows a simplified scenario with two isotropic Gaussians (giso) and two anisotropic Gaussians (gdir) along a ray. The figure demonstrates that if the Gaussian sets are rendered separately, the anisotropic Gaussian (gdir1) behind the isotropic Gaussian (giso2) would incorrectly contribute to the overall ray absorption. Joint rasterization ensures that the correct occlusion relationships are accounted for, resulting in a more accurate representation of X-ray image formation.

More on tables

This table compares the performance of three different Gaussian splatting-based methods for digitally reconstructed radiograph (DRR) rendering on two datasets (NAF-CT and CTPelvic1K). The methods compared are DDGS (the authors’ proposed method), X-Gaussian, and a baseline 3DGS method. For each dataset and method, the table shows the number of points used in the 3D Gaussian splatting representation, along with the peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) values, which are used to assess the quality of the rendered DRRs. The results demonstrate that the authors’ DDGS method achieves superior performance in terms of both PSNR and SSIM compared to the other techniques, suggesting that their method produces higher quality DRRs.

This table presents the ablation study comparing the proposed disentangled isotropic/anisotropic representations with other methods such as direct-entangled, direct-independent, direct-dependent, and 3DGS-disentangled. The results (PSNR and SSIM) are shown for two datasets (001 and 002) to demonstrate the effectiveness of the proposed method in improving image quality.

This table compares the performance of three different Gaussian splatting-based DRR rendering techniques (DDGS, X-Gaussian, and 3DGS) across two datasets (NAF-CT and CTPelvic1K). For each method and dataset, the table shows the number of points used in the Gaussian splatting model, and the resulting PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity Index) scores, which measure the quality of the rendered DRRs. Higher PSNR and SSIM values indicate better image quality.

This table shows the impact of the feature dimension (k) on the image quality (PSNR and SSIM) for two scans (001 and 002) from the CTPelvic1K dataset. It demonstrates how increasing k improves both PSNR and SSIM, but the improvement becomes marginal after k exceeds 16. This highlights the trade-off between model complexity and performance gains.

This table presents a comparison of the accuracy of image registration achieved by different methods on the CTPelvic1K dataset. The metrics used are rotation error (in degrees) and translation error (in millimeters). Lower values indicate better registration performance. The comparison includes 3DGS [17], X-Gaussian [7] with k=8 and k=32, and the proposed DDGS method. The results are shown for three different scans (001, 002, 003) from the dataset.

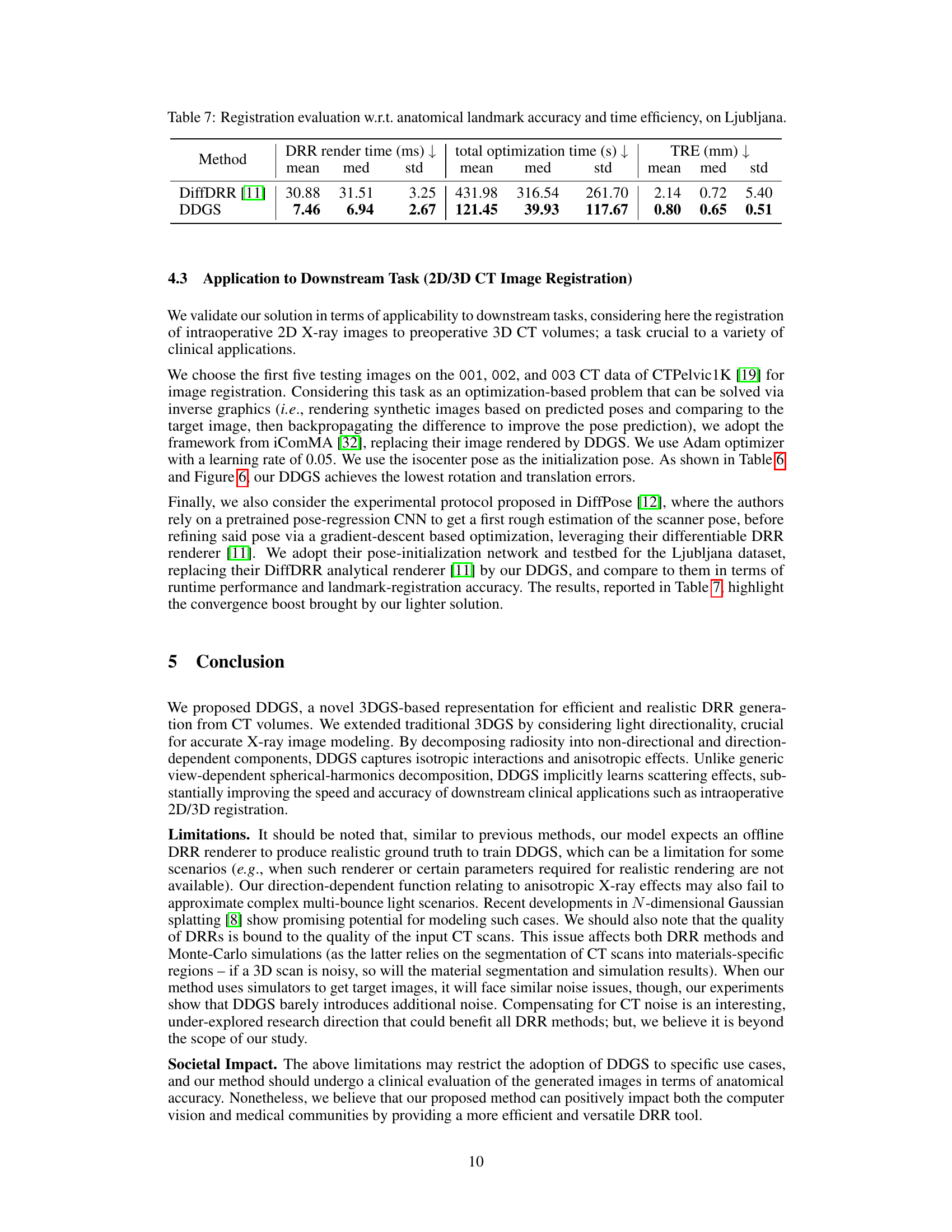
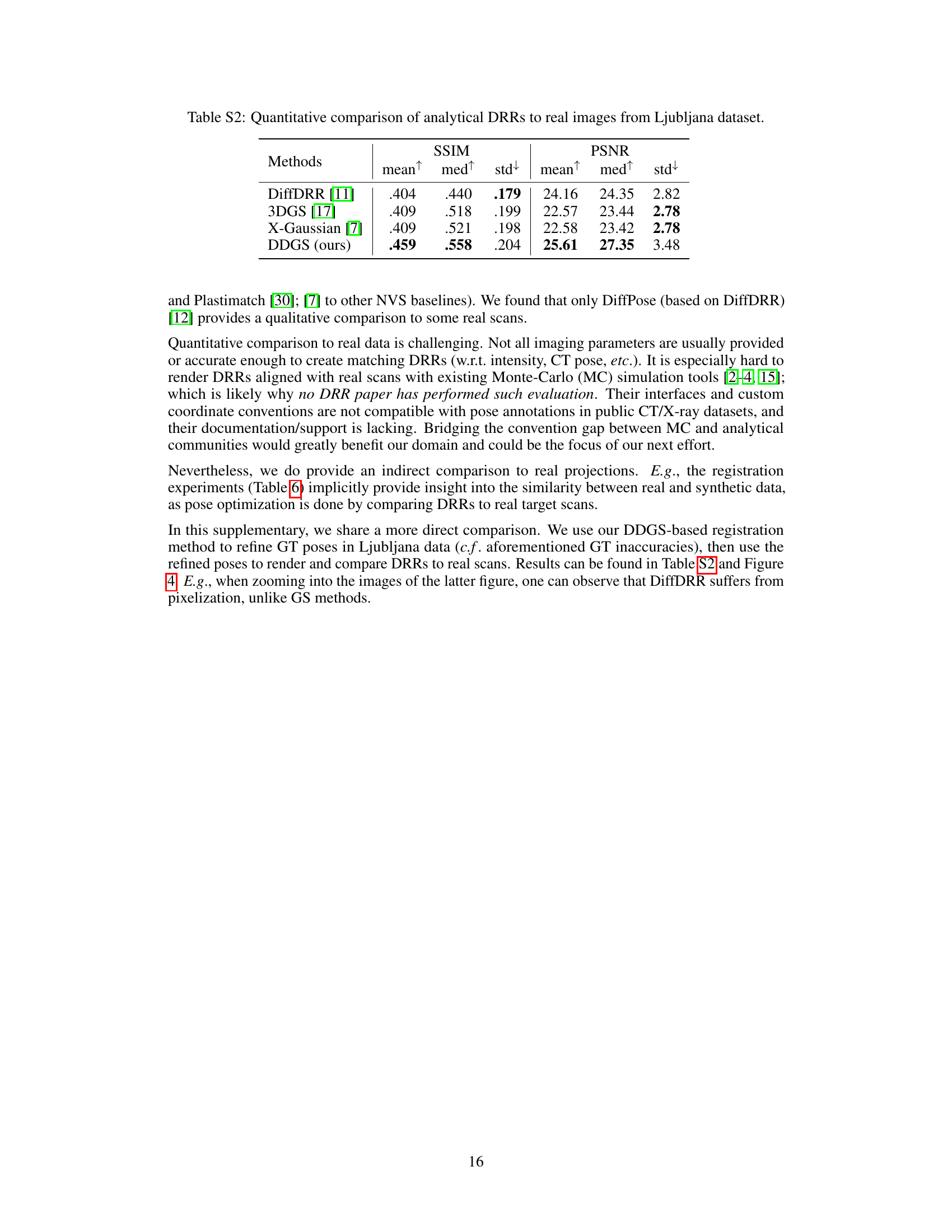
This table presents a comparison of the proposed DDGS method with the DiffDRR method [11] for 2D/3D CT image registration using the Ljubljana dataset [26]. The evaluation metrics include DRR render time, total optimization time, and target registration error (TRE) in millimeters. The results demonstrate that DDGS achieves superior registration accuracy and significantly faster runtime performance compared to DiffDRR.

This table compares the performance of different Gaussian splatting-based methods for DRR rendering on two datasets: NAF-CT and CTPelvic1K. It shows the PSNR and SSIM scores achieved by each method, along with the number of Gaussian points used. The comparison includes 3DGS [17], X-Gaussian [7], and the proposed DDGS method, demonstrating the superior performance of DDGS in terms of both image quality metrics.

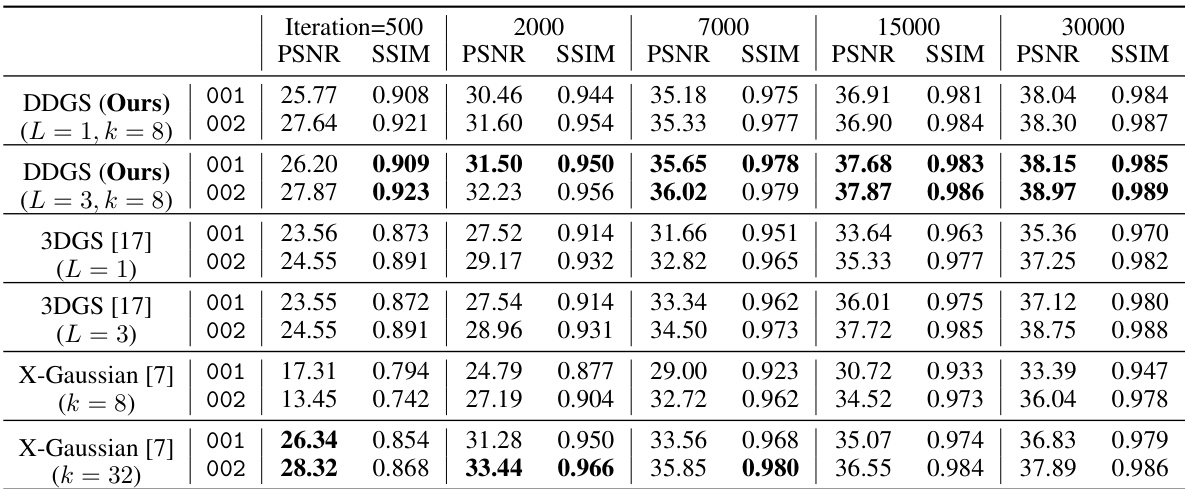
This table presents a comparison of novel-view synthesis results on the CTPelvic1K dataset. It shows the PSNR and SSIM metrics for different methods (DDGS, 3DGS, and X-Gaussian) and different numbers of iterations (500, 2000, 7000, 15000, and 30000). The results are shown separately for two CT scans (001 and 002) to demonstrate the variation in performance across different subjects.

Full paper

#