TL;DR#
Large language models (LLMs) exhibit unexpected capabilities, but evaluating and aligning them poses a challenge. The paper addresses the intriguing phenomenon where finetuning strong LLMs with labels generated by weaker models results in improved performance, a concept known as ‘weak-to-strong generalization.’ This raises questions about how effectively weak supervision can guide strong models.
This research introduces a theoretical framework to explain weak-to-strong generalization. The core idea revolves around ‘misfit error,’ which measures the discrepancy between the strong model’s performance on labels generated by a weaker model and the ground truth. The authors demonstrate that the gain in accuracy from using this methodology is directly related to this misfit. They validate their theoretical findings through empirical experiments.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a theoretical framework for understanding and quantifying the surprising phenomenon of weak-to-strong generalization in large language models. This is a critical area of research as it directly impacts the development and alignment of increasingly powerful AI models. The insights provided open avenues for developing new algorithmic heuristics and improving model training.
Visual Insights#

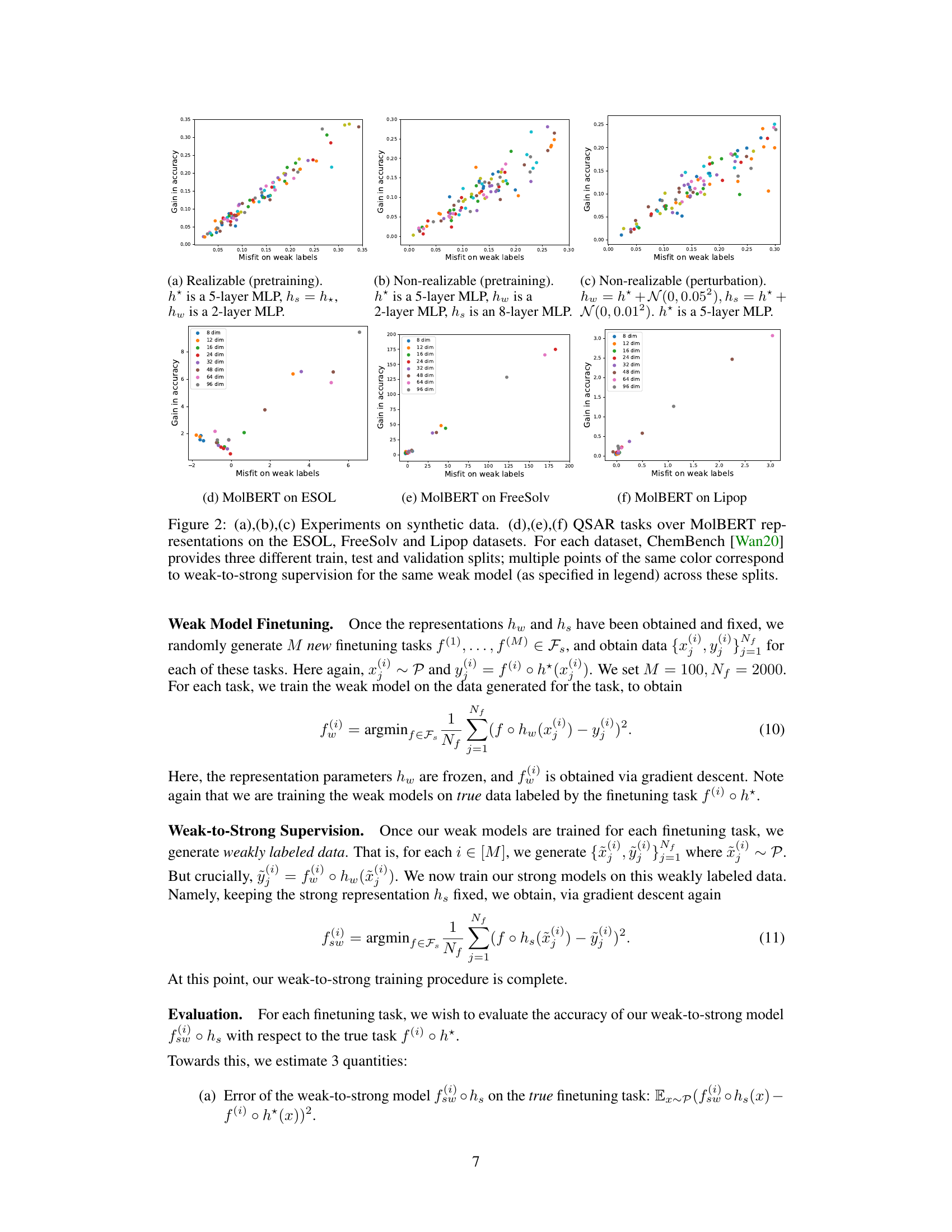
🔼 This figure is a geometric illustration of the main theoretical result (Theorem 1) in the paper. It shows the relationship between the true target function (f* o h*), the weak model’s prediction (fw o hw), and the strong model’s prediction (fsw o hs). The green ellipse represents the convex set Vs of functions attainable by the strong model, and the point f* o h* lies within this set. The point fsw o hs is the projection of fw o hw onto the set Vs, and the distances A, B, C between these points represent the error terms involved in the theorem. The Pythagorean-like relationship between A, B, and C visually demonstrates that the error of the strong model trained with weak supervision is less than or equal to the error of the weak model minus the improvement the strong model makes.
read the caption
Figure 1: fsw o hs is the projection of fw o hw onto the convex set Vs.
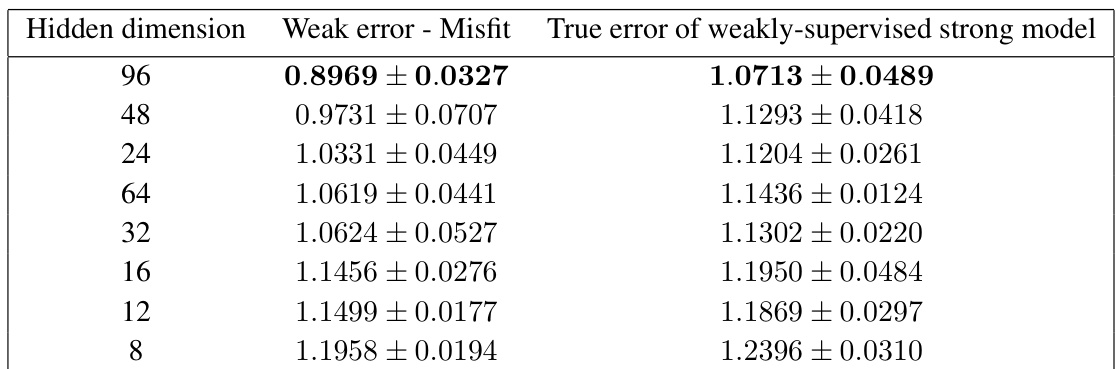
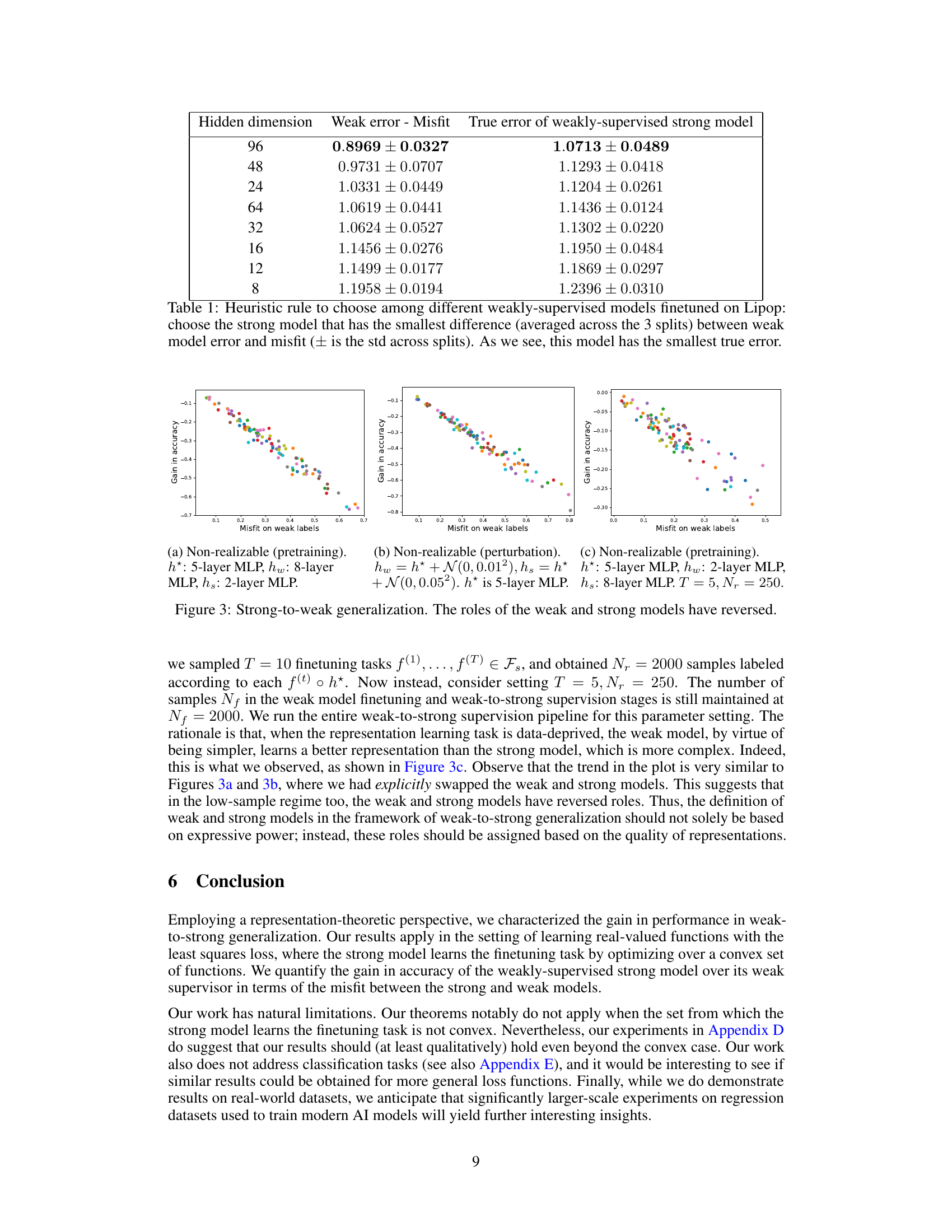
🔼 This table presents a heuristic for choosing among different weakly supervised models when fine-tuning on the Lipop dataset. It shows the weak model error minus the misfit, the true error of the weakly supervised strong model, and the hidden dimension for each model. The heuristic suggests selecting the model with the smallest difference between the weak model error and the misfit, as this tends to result in the lowest true error for the strong model.
read the caption
Table 1: Heuristic rule to choose among different weakly-supervised models finetuned on Lipop: choose the strong model that has the smallest difference (averaged across the 3 splits) between weak model error and misfit (± is the std across splits). As we see, this model has the smallest true error.
In-depth insights#
Weak-to-Strong Gains#
The concept of “Weak-to-Strong Gains” in the context of AI model training refers to the surprising phenomenon where a strong model, fine-tuned using labels generated by a weaker model, outperforms both the weak and independently trained strong models. This counterintuitive result challenges conventional wisdom. A key insight is that the improvement achieved by the strong model is directly proportional to the ‘misfit’ between the strong model’s predictions and the weaker model’s labels. This misfit, rather than being a source of error, serves as a form of indirect supervision, guiding the strong model toward superior performance on the actual task. The theoretical framework presented helps quantify this gain, suggesting that the strong model leverages the weaker model’s implicit knowledge, effectively rectifying its inaccuracies while still benefitting from its guidance. The framework’s strength lies in its representation-theoretic perspective, which highlights the disparity in data representation quality between weak and strong models as the primary factor. This disparity is linked to differences in model complexity and pretraining data. The results across various synthetic and real-world experiments consistently validate the theoretical findings, showcasing the robustness and applicability of the proposed framework in understanding and predicting weak-to-strong generalization.
Theoretical Framing#
The theoretical framing of weak-to-strong generalization centers on a representation-theoretic perspective, highlighting the disparity in data representation quality between weak and strong models. This disparity, stemming from differences in model expressivity, complexity, and pretraining data, is crucial. The core idea is that finetuning tasks are simpler functions composed with these representations. The theory quantifies the accuracy gain of a strong model trained on weak labels, showing it’s at least the misfit error—the error the strong model incurs on the weak model’s labels. This misfit error directly quantifies the erroneous knowledge the strong model doesn’t obtain from the weak model, thus explaining the performance improvement. The theoretical analysis involves a realizable setting where the target task is within the strong model’s function class, and a non-realizable setting, relaxing this constraint and accounting for finite samples. The results demonstrate a direct link between the gain in accuracy and the strong-weak model misfit, providing a theoretical foundation for the empirically observed weak-to-strong generalization phenomenon.
Empirical Validation#
An empirical validation section in a research paper would rigorously test the study’s theoretical claims. This would involve designing experiments with well-defined metrics and appropriate controls to demonstrate the relationship between weak and strong models, as predicted by the theoretical framework. Synthetic datasets are useful for isolating variables, while real-world data (molecular prediction, NLP tasks) enhances generalizability. Success hinges on demonstrating a strong correlation between predicted performance gains (based on misfit error) and actual observed gains, across diverse experimental settings and datasets. Statistical significance testing would be crucial. The section should also address potential confounding factors and discuss any deviations from theoretical predictions, providing a nuanced interpretation of the results and acknowledging limitations. Careful consideration of datasets, experimental design, and statistical analysis is vital for convincing evidence and robust conclusions.
Algorithmic Insights#
The study’s algorithmic insights revolve around quantifying the gain in weak-to-strong generalization through a novel metric: the misfit error. This error measures the difference between a strong model’s predictions and those of a weaker model, revealing how much the strong model learns from the weak model’s labels. Importantly, the misfit error is shown to directly predict the improvement the strong model exhibits over its weaker counterpart. This suggests practical strategies for selecting the most effective weak model to use for training a strong model – choosing the one with the smallest difference between its error and its misfit with the strong model. The study also proposes the potential to improve generalization even further by ensembling multiple weak models. This work provides a theoretical basis for understanding the phenomenon of weak-to-strong generalization, suggesting potential for improved training methodologies and a more robust understanding of large language models.
Future Directions#
Future research could explore extending the theoretical framework beyond regression and least-squares loss to encompass classification tasks and other loss functions. Investigating the impact of different types of disagreement between weak and strong models on the overall gain in accuracy is crucial for a more comprehensive understanding. The interplay between model expressiveness, representation quality, and the amount of pretraining data deserves further study. Exploring the effect of varying the size and quality of the weak-model training data is another promising area. Furthermore, developing efficient algorithms for selecting and ensembling weak models to maximize the gain in weak-to-strong generalization would be highly valuable. Finally, it is important to investigate the practical implications and potential limitations of this weak-to-strong generalization method in real-world applications, considering factors such as data scarcity and computational constraints. Robustness analysis is essential to determine the sensitivity of the results to variations in data distribution, model architecture, and hyperparameters.
More visual insights#
More on figures

🔼 This figure displays the results of experiments on synthetic and real-world datasets. The synthetic data experiments (a, b, c) show the relationship between the misfit error and the gain in accuracy for different model setups (realizable and non-realizable, with pretraining and perturbation). The real-world datasets (d, e, f) are from the QSAR tasks using MolBERT representations. Each QSAR dataset has three train/test/validation splits, and multiple points for each weak model are plotted to represent results across these splits. The plots show the gain in accuracy versus the misfit on weak labels. The main observation is that the gain in accuracy is strongly correlated with the misfit error, verifying the paper’s theoretical findings.
read the caption
Figure 2: (a),(b), (c) Experiments on synthetic data. (d), (e),(f) QSAR tasks over MolBERT representations on the ESOL, FreeSolv and Lipop datasets. For each dataset, ChemBench [Wan20] provides three different train, test and validation splits; multiple points of the same color correspond to weak-to-strong supervision for the same weak model (as specified in legend) across these splits.

🔼 The figure shows the results of experiments on synthetic and real-world datasets. Synthetic experiments (a-c) illustrate the relationship between the gain in accuracy from weak-to-strong supervision and the misfit on weak labels for different model architectures and data generation methods (realizable and non-realizable settings). Real-world experiments (d-f) use the MolBERT model on three QSAR datasets (ESOL, FreeSolv, Lipop) to further demonstrate the relationship between gain in accuracy and misfit. Each dataset has three train/test/validation splits, and the multiple data points of the same color represent results of weak-to-strong supervision using the same weak model across the splits.
read the caption
Figure 2: (a),(b), (c) Experiments on synthetic data. (d), (e),(f) QSAR tasks over MolBERT representations on the ESOL, FreeSolv and Lipop datasets. For each dataset, ChemBench [Wan20] provides three different train, test and validation splits; multiple points of the same color correspond to weak-to-strong supervision for the same weak model (as specified in legend) across these splits.

🔼 This figure is a geometric illustration to help understand the proof of Theorem 1. The convex set Vs represents all functions that can be obtained by composing a function from the convex set Fs with the strong model’s representation hs. The point f* o h* represents the true target function composed with the ground truth representation. The point fw o hw is the function learned by the weak model. fsw o hs is the projection of fw o hw onto Vs, the closest point in Vs to fw o hw. The distances A, B and C represent the distances between these points and are used in the proof’s triangle inequality argument to show the relationship between the error of the weakly supervised strong model, the error of the weak model and the misfit between the strong and weak model.
read the caption
Figure 1: fsw o hs is the projection of fw o hw onto the convex set Vs.

🔼 This figure displays the results of experiments on synthetic and real-world datasets. The synthetic data experiments show the relationship between misfit (disagreement between weak and strong models) and gain in accuracy (improvement of the strong model over the weak model). The real-world experiments use MolBERT representations for QSAR tasks on ESOL, FreeSolv, and Lipop datasets, demonstrating the relationship across various train/test/validation splits. Each point represents a weak-to-strong supervision experiment with a different weak model.
read the caption
Figure 2: (a),(b), (c) Experiments on synthetic data. (d), (e),(f) QSAR tasks over MolBERT representations on the ESOL, FreeSolv and Lipop datasets. For each dataset, ChemBench [Wan20] provides three different train, test and validation splits; multiple points of the same color correspond to weak-to-strong supervision for the same weak model (as specified in legend) across these splits.
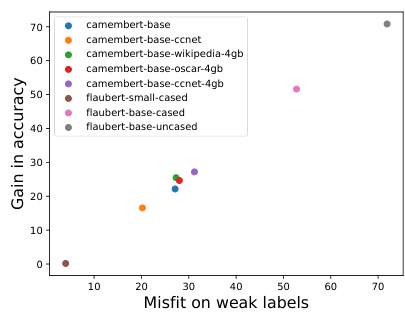
🔼 This figure shows the results of the weak-to-strong generalization experiment on the French Reviews dataset. The x-axis represents the misfit on weak labels, and the y-axis represents the gain in accuracy. Each point represents a different weak model used in the experiment, showing how well the gain in accuracy of the strong model is correlated with the misfit on weak labels. Different colored points represent different weak models (CamemBERT and Flaubert variants).
read the caption
Figure 6: Results on the French Reviews dataset.

🔼 This figure shows the results of experiments on synthetic and real-world data. The synthetic data experiments (a-c) demonstrate the relationship between the gain in accuracy from weak-to-strong supervision and the misfit (disagreement) between the weak and strong models under different conditions (realizable vs. non-realizable, different representation learning methods). The real-world experiments (d-f) use the MolBERT model on three QSAR datasets (ESOL, FreeSolv, Lipop) to further validate the findings, showing that the gain in accuracy correlates with the misfit across different weak models and data splits.
read the caption
Figure 2: (a),(b), (c) Experiments on synthetic data. (d), (e),(f) QSAR tasks over MolBERT representations on the ESOL, FreeSolv and Lipop datasets. For each dataset, ChemBench [Wan20] provides three different train, test and validation splits; multiple points of the same color correspond to weak-to-strong supervision for the same weak model (as specified in legend) across these splits.
More on tables
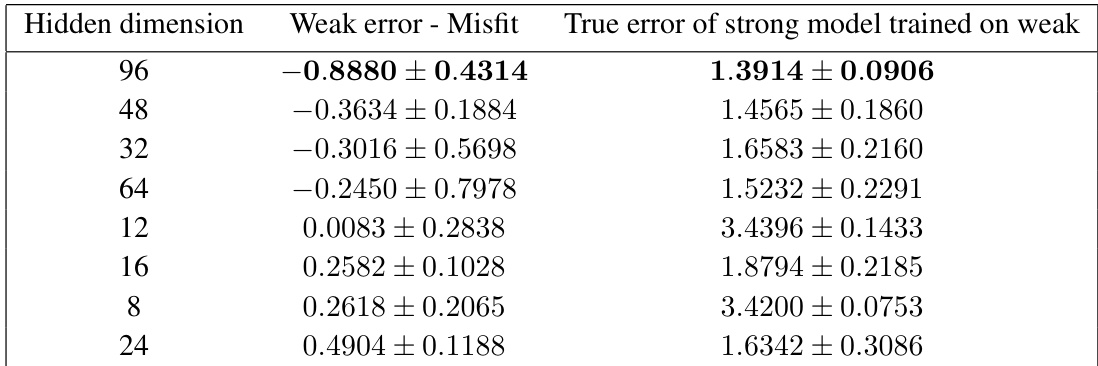
🔼 This table presents results from experiments on the ESOL dataset, demonstrating a heuristic for choosing among different weakly-supervised models based on minimizing the difference between weak model error and misfit. The table shows, for various hidden dimensions of the weak model, the calculated ‘Weak error - Misfit’ and the resulting ‘True error of strong model trained on weak’. The goal is to identify the strong model that achieves the lowest true error by selecting the weak model that minimizes the given difference.
read the caption
Table 2: ESOL
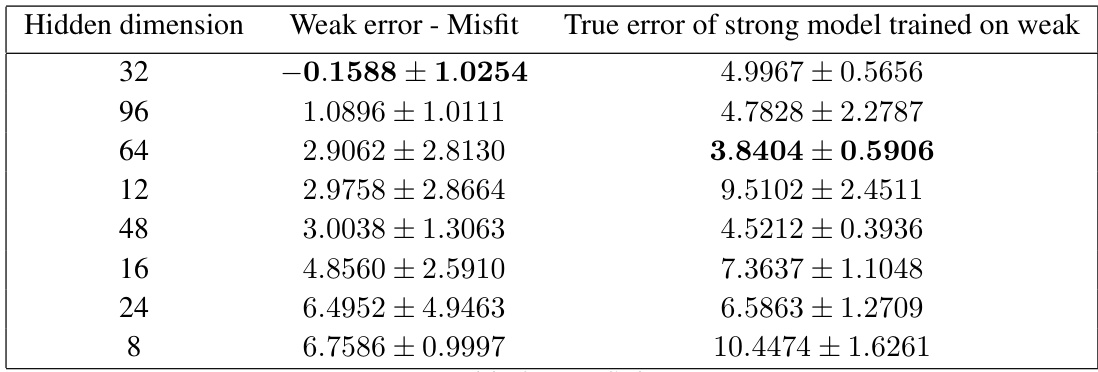
🔼 This table presents the results of applying a heuristic rule for choosing among different weakly supervised models that were fine-tuned on the FreeSolv dataset. For each hidden dimension of the weak model, the table shows the difference between the weak model error and the misfit error, as well as the true error of the strong model trained using the weak labels. The heuristic suggests selecting the strong model with the smallest difference between the weak model error and the misfit, as this tends to correspond to the strong model with the lowest true error.
read the caption
Table 3: FreeSolv
Full paper#