TL;DR#
Canonical Correlation Analysis (CCA) faces challenges in high-dimensional data due to its difficulty in explaining correlations between variable sets and its poor interpretability. Sparse CCA (SCCA) aims to address this by finding sparse linear combinations of variables, improving interpretability. However, existing SCCA methods often lack strong formulations and efficient algorithms, particularly when dealing with low-rank covariance matrices. This often results in NP-hard problems.
This paper presents strong formulations and efficient algorithms for SCCA. The researchers introduce a combinatorial formulation for SCCA, providing a foundation for approximation algorithms and enabling analysis of low-rank special cases. They also derive an equivalent MISDP reformulation, leading to a specialized branch-and-cut algorithm that is shown to be effective in numerical experiments on both synthetic and real-world datasets. This makes SCCA applicable to larger datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with high-dimensional data, as it introduces efficient algorithms and formulations for Sparse Canonical Correlation Analysis (SCCA). SCCA enhances the interpretability of traditional CCA by identifying sparse linear combinations of variables, making it particularly valuable for domains like genomics where data sets are often large and complex. The paper’s findings open new avenues for research by providing strong theoretical foundations, including complexity analysis and equivalent MISDP reformulations, thereby paving the way for improved SCCA applications. This work is particularly timely because of the increasing interest in high-dimensional data analysis across various fields.
Visual Insights#

🔼 This figure shows the correlation between Sparse Canonical Correlation Analysis (SCCA) and CCA for various sparsity levels (s1, s2) on a real UCI dataset (n=28, m=29). The heatmap visualizes the ratio of correlations between SCCA and CCA for different combinations of s1 and s2. It provides insights into the maximum sparsity that SCCA can achieve while maintaining a high correlation with the full data.
read the caption
Figure 1: On UCI data with n, m = 28, 29
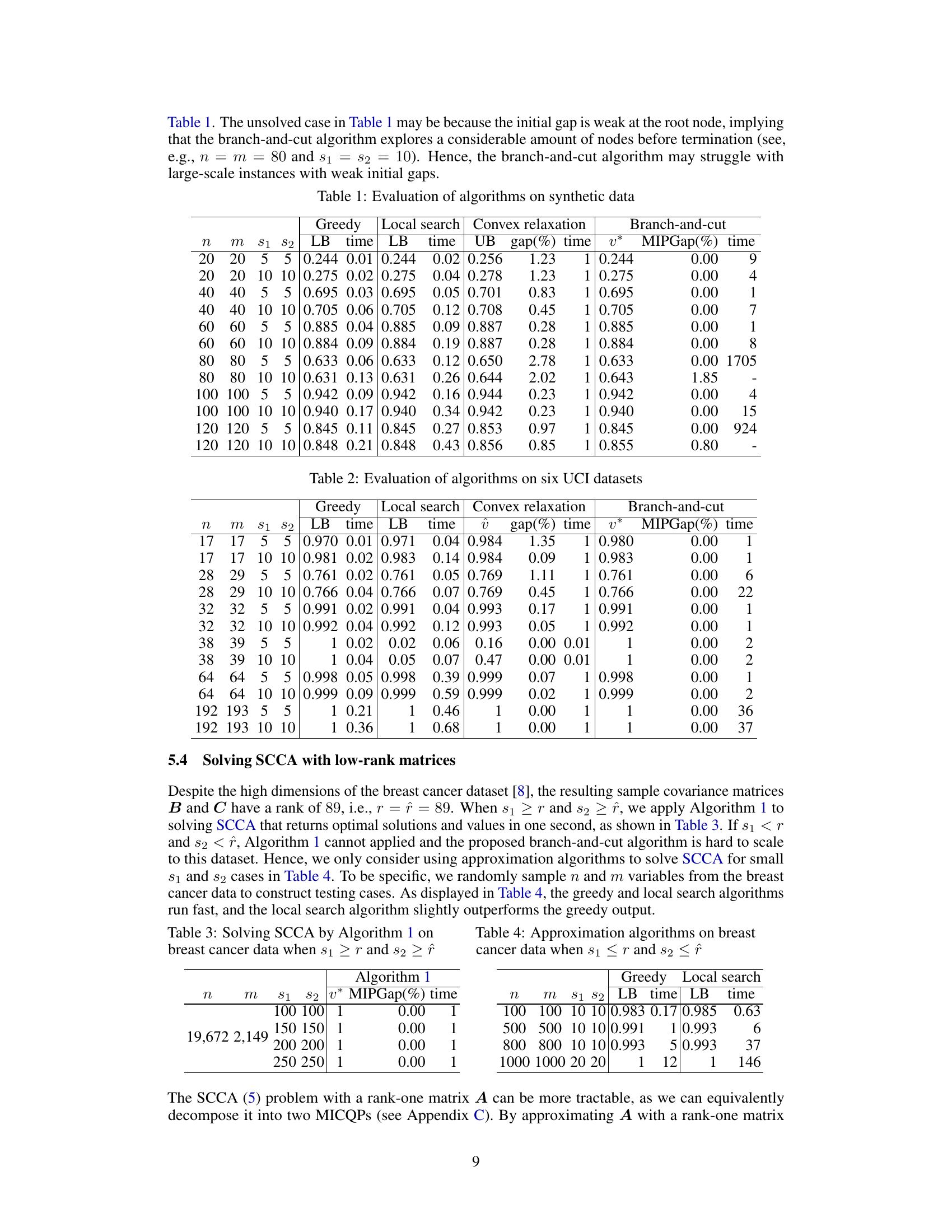
🔼 This table presents a comparison of the performance of three algorithms (Greedy, Local search, and Branch-and-cut) in solving the SCCA problem on synthetic datasets with varying dimensions and sparsity levels. The table shows the lower bound (LB), running time, upper bound (UB), optimality gap, final solution (v*), and MIP gap for each algorithm and dataset configuration. The results demonstrate the scalability and accuracy of the algorithms under different conditions.
read the caption
Table 1: Evaluation of algorithms on synthetic data
In-depth insights#
Sparse CCA Generalization#
Sparse Canonical Correlation Analysis (CCA) enhances the interpretability of traditional CCA by encouraging sparsity in the resulting canonical vectors. A key aspect to consider is how sparse CCA generalizes to other well-known sparse optimization problems. It’s crucial to demonstrate that sparse CCA encompasses problems like sparse PCA, sparse SVD, and sparse regression, all of which are computationally challenging (NP-hard). This generalization is significant because it reveals a unifying framework, demonstrating that techniques developed for sparse CCA can potentially be adapted to solve other sparse problems. Understanding the relationships between these problems is vital for developing efficient and effective algorithms, since a solution for one could inform solutions for the others. Exploring the generalization further by focusing on low-rank instances of the covariance matrices could reveal further computational advantages. This analysis might reveal polynomial-time solutions under certain conditions, significantly impacting the scalability of sparse CCA. Finally, the study of these generalizations could inspire novel algorithmic strategies, possibly yielding more efficient approaches than those currently available for individual sparse problems.
Complexity of SCCA#
The complexity of Sparse Canonical Correlation Analysis (SCCA) is a critical aspect of its applicability to high-dimensional datasets. The problem’s inherent difficulty stems from its generalization of NP-hard problems like sparse PCA and sparse regression. Low-rank structures in the covariance matrices (B and C) significantly impact complexity. When the sparsity levels (s1, s2) exceed or equal the ranks (r, r̂) of B and C respectively, SCCA reduces to the simpler CCA problem, solvable in polynomial time. However, the general case remains NP-hard. Approximation algorithms, such as greedy and local search methods, offer practical solutions, although they lack optimality guarantees. Further research could focus on developing more sophisticated approximation algorithms or exploring alternative formulations of SCCA that are less computationally demanding, perhaps by leveraging the low-rank structure of real-world datasets more effectively. The introduction of mixed-integer semidefinite programming (MISDP) provides a novel approach for solving SCCA exactly, but comes with its own computational challenges, specifically concerning scalability.
MISDP Reformulation#
The MISDP (Mixed-Integer Semidefinite Programming) reformulation section of a research paper would likely focus on transforming a difficult combinatorial optimization problem, such as Sparse Canonical Correlation Analysis (SCCA), into an equivalent MISDP. This is a crucial step because MISDP problems, while still complex, are often more amenable to solution via established optimization solvers and techniques. The reformulation likely involves introducing binary variables to enforce sparsity constraints and expressing the original objective and constraints in a semidefinite programming form. This approach provides a path to finding exact or provably near-optimal solutions to SCCA, which is usually NP-hard, unlike many heuristic or approximation methods that might only yield suboptimal results. The authors might discuss the challenges in developing this reformulation, such as managing the increased problem size and complexity introduced by the binary variables. A key part of this section might be demonstrating the equivalence between the original combinatorial formulation and the MISDP, ensuring that any solution found in the MISDP setting maps directly back to a solution for the initial problem. The computational implications of the reformulation, the size and scalability of the resulting MISDP model, and how it compares to other solution strategies would also be addressed. In short, the reformulation provides a bridge between the original problem and the realm of exact solution methods. Therefore, the success of this approach hinges on how effectively the reformulation leverages the power of MISDP techniques without introducing intractable computational costs. The efficacy of this reformulation is likely validated via computational experiments, comparing the MISDP-based results to solutions obtained using other techniques.
Low-Rank SCCA#
The section on “Low-Rank SCCA” delves into scenarios where the covariance matrices (B and C) exhibit low rank, a common occurrence in high-dimensional datasets with limited samples. This low-rank property significantly impacts the computational complexity of solving the SCCA problem. The authors explore two special cases. First, when the sparsity levels (s1, s2) meet or exceed the ranks of B and C, the zero-norm constraints become redundant, simplifying the problem to a computationally cheaper CCA. Second, when the cross-covariance matrix (A) is rank-one, SCCA reduces to two independent sparse regression problems, which are themselves NP-hard but offer improved scalability compared to the general SCCA problem. These findings highlight the importance of considering data characteristics, specifically matrix rank, when designing efficient algorithms for SCCA. The exploration of low-rank cases not only provides complexity analysis but also paves the way for developing polynomial-time exact algorithms and more efficient approximation strategies in specific low-rank scenarios. This section provides valuable insights into solving SCCA under realistic data constraints, ultimately contributing to the practical applicability of SCCA in high-dimensional data analysis.
Algorithm Efficiency#
The algorithm efficiency analysis in this research paper is crucial for understanding its practical applicability. Computational complexity is addressed, particularly regarding the NP-hard nature of the Sparse Canonical Correlation Analysis (SCCA) problem. The authors propose several algorithmic approaches including SDP relaxations and branch-and-cut methods, acknowledging the limitations of each. Polynomial-time algorithms are developed for specific low-rank instances of SCCA, highlighting cases where efficient exact solutions are achievable. Approximation algorithms, such as greedy and local search, are also introduced to handle larger, more complex cases, although their optimality isn’t guaranteed. The paper provides empirical results to demonstrate the performance and scalability of the different methods. Comparison with existing SCCA algorithms shows the effectiveness of the novel approaches in terms of both speed and accuracy. The detailed computational analysis, along with both theoretical and experimental results, contributes significantly to our understanding of how to efficiently solve the SCCA problem under various circumstances.
More visual insights#
More on tables
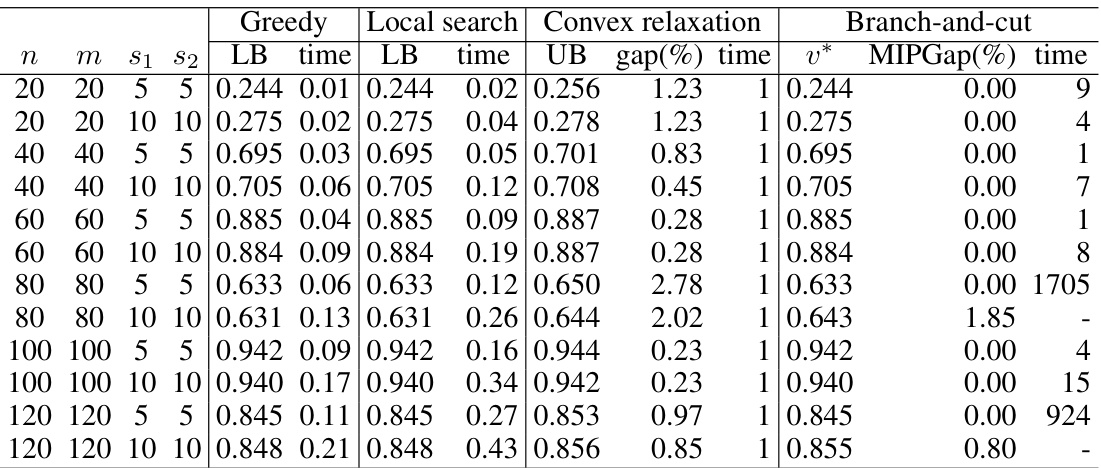
🔼 This table presents a comparison of four algorithms (Greedy, Local search, Convex relaxation, and Branch-and-cut) for solving the Sparse Canonical Correlation Analysis (SCCA) problem on synthetic datasets with varying parameters (n, m, s1, s2). For each algorithm and parameter set, it shows the lower bound (LB), the time taken, the upper bound (UB), the optimality gap, and the final optimal value (v*) achieved by the branch-and-cut algorithm along with its optimality gap (MIPGap) and runtime. The results demonstrate the scalability and performance of the algorithms under different sparsity levels.
read the caption
Table 1: Evaluation of algorithms on synthetic data

🔼 This table presents the results of applying Algorithm 1 to solve SCCA on the breast cancer dataset, where the ranks of covariance matrices B and C (r and r̂) are both 89. The algorithm is applied with sparsity levels (s₁, s₂) exceeding the ranks of B and C (s₁ > r and s₂ ≥ r̂). It shows that the algorithm finds optimal solutions very quickly even for a dataset as large as the breast cancer dataset (19,672, 2,149 variables). The table displays the optimal value (v*), the optimality gap (MIPGap%), and the computation time for different sparsity levels (s₁, s₂).
read the caption
Table 3: Solving SCCA by Algorithm 1 on breast cancer data when s₁ > r and s₂ ≥ r

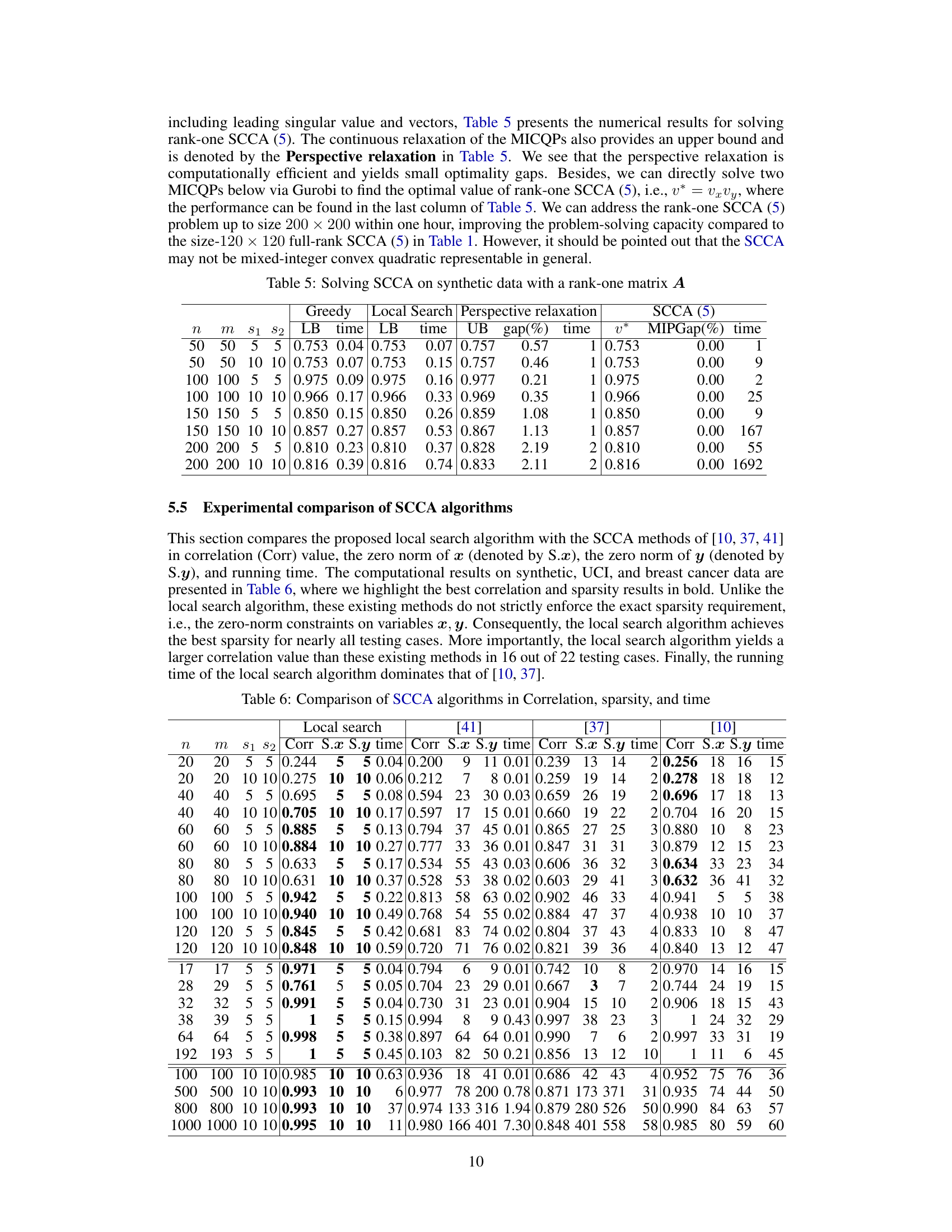
🔼 This table presents the numerical results for solving rank-one SCCA. It compares the performance of greedy and local search algorithms against the perspective relaxation method, showing the lower bound (LB), upper bound (UB), optimality gap, and the optimal value (v*) obtained by solving the Mixed-Integer Convex Quadratic Programs (MICQPs) for rank-one SCCA. The table includes various parameters like n (number of variables in the first set), m (number of variables in the second set), s1 (sparsity level for the first set), s2 (sparsity level for the second set), and k (number of pairs of basis vectors). The results demonstrate the efficiency and accuracy of these methods for solving rank-one SCCA problems.
read the caption
Table 5: Solving SCCA on synthetic data with a rank-one matrix A
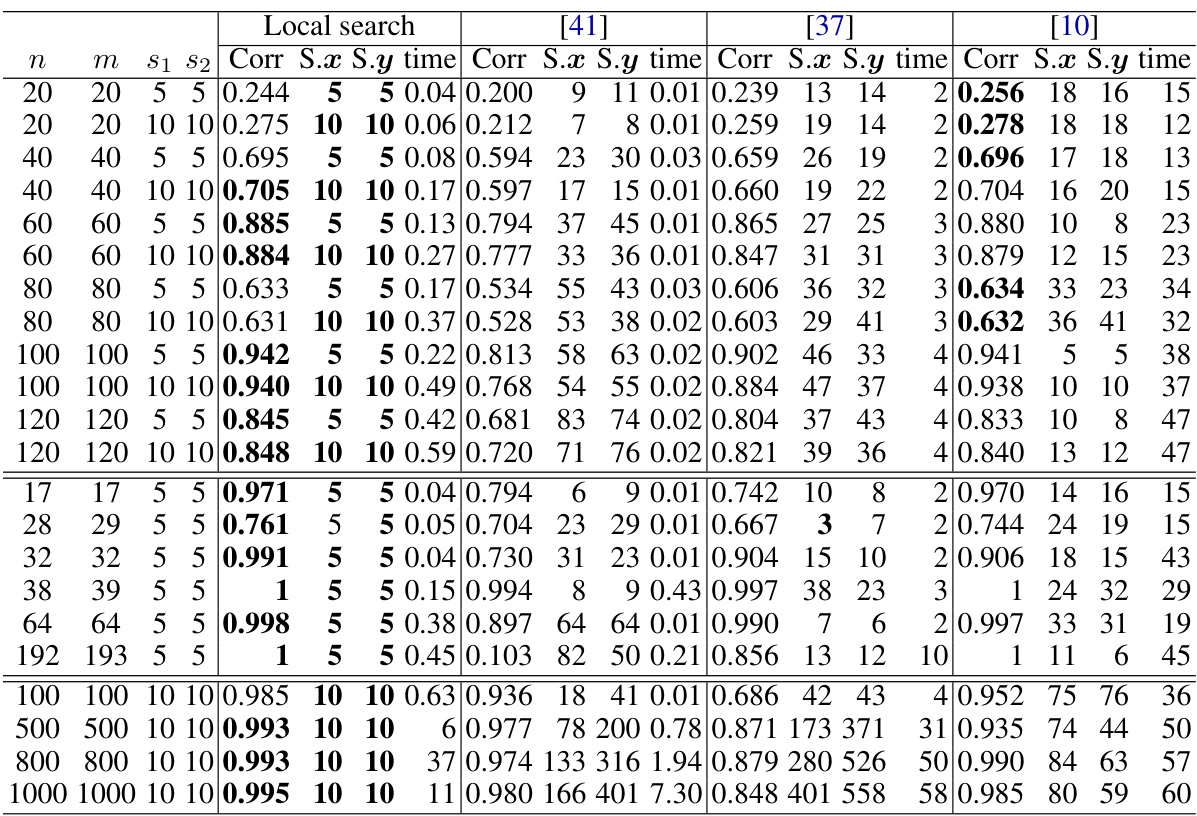
🔼 This table compares the performance of the proposed local search algorithm with three other existing SCCA methods ([10, 37, 41]) across various datasets. The comparison is based on correlation values, sparsity levels (measured by the zero norms of x and y), and computation time. The results show that the local search algorithm often achieves better sparsity and comparable or superior correlation results, although with potentially higher computation times.
read the caption
Table 6: Comparison of SCCA algorithms in Correlation, sparsity, and time

🔼 This table presents the characteristics of seven datasets used in the paper’s numerical experiments. For each dataset, it lists the number of variables, the number of samples, the number of variables assigned to the first set (n), the number of variables assigned to the second set (m), and the ranks of the covariance matrices B and C (r and r̂, respectively). The datasets include several UCI datasets and a breast cancer dataset, demonstrating varying sizes and characteristics.
read the caption
Table 7: Description of UCI and breast cancer datasets used

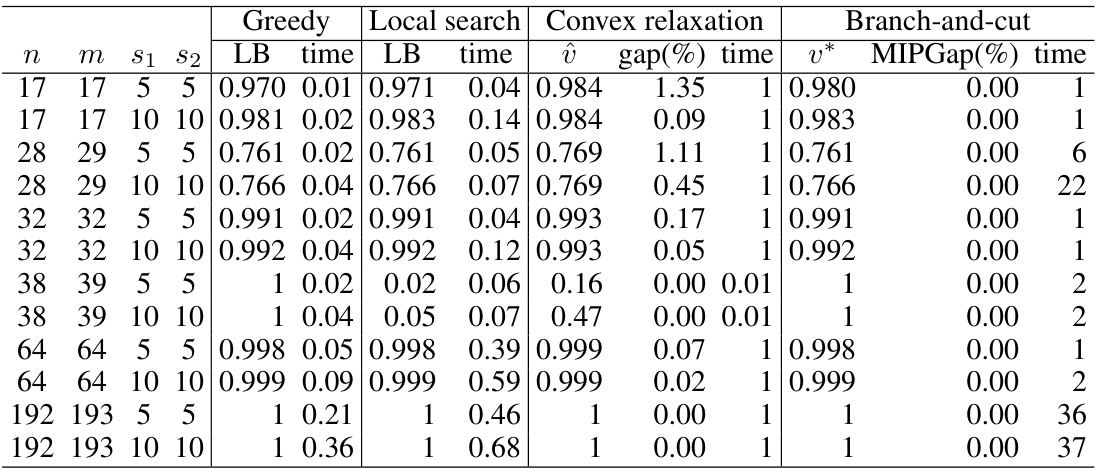
🔼 This table presents a comprehensive evaluation of the proposed algorithms (Greedy, Local search, Convex relaxation, Branch-and-cut) for solving the Multiple Sparse Canonical Correlation Analysis (SCCA) problem on six UCI datasets. For each dataset, various parameters (n, m, s1, s2, k) are tested, representing the number of variables in each set, sparsity levels, and the number of canonical vectors. The table shows the lower bound (LB), time taken, and optimality gap for each algorithm. The branch-and-cut algorithm aims to provide optimal solutions, but its computation time can increase significantly for larger problems.
read the caption
Table 8: Evaluation of our algorithms for solving multiple SCCA on UCI datasets
Full paper#