Efficient Graph Matching for Correlated Stochastic Block Models

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it efficiently solves a long-standing open problem in graph matching for correlated stochastic block models, a widely used model for network data analysis. This opens new avenues for research in various fields that rely on network data analysis, and provides efficient algorithms with strong theoretical guarantees, advancing the state-of-the-art in graph matching.

Visual Insights

#

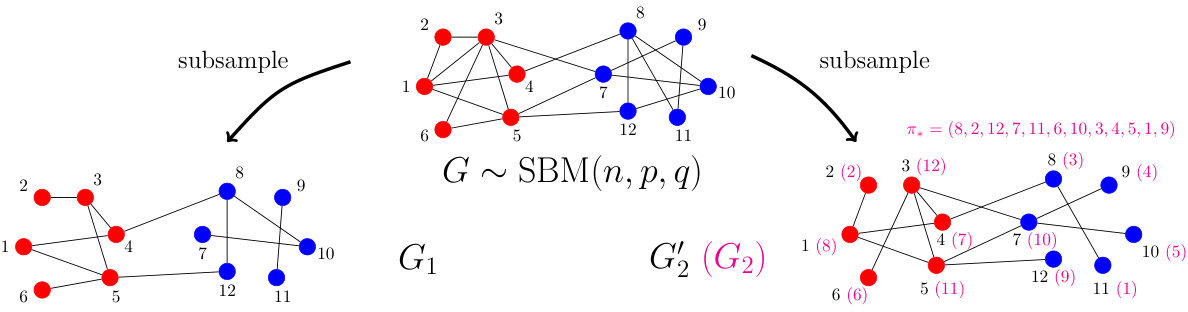
The figure illustrates the generation process of two correlated stochastic block models (CSBMs) with two balanced communities. It starts with a parent graph generated from a standard stochastic block model (SBM), where nodes are assigned to one of two communities (+1 or -1) and edges are formed independently with probabilities that depend on the community memberships of the connected nodes. Then, two child graphs, G1 and G2, are created by subsampling edges from the parent graph independently. Each edge in the parent graph has a probability s of being included in G1 and independently a probability s of being included in G2. Finally, the nodes in G2 are permuted according to a random permutation π* to break the direct correspondence between the nodes of G1 and G2, resulting in two correlated SBMs that share the same community structure but with permuted nodes.

In-depth insights

#

Correlated SBMs

#

The concept of “Correlated SBMs,” or correlated stochastic block models, is a crucial extension of standard SBMs. It introduces a crucial layer of realism by acknowledging that real-world networks often exhibit correlation between different observations or snapshots of the same underlying network structure. This correlation is not only practically relevant but also fundamentally alters the information-theoretic and algorithmic challenges associated with various inference tasks. In correlated SBMs, multiple graphs are generated from a shared community structure, with edge presence in different graphs related via a correlation parameter. The primary advantage is the ability to leverage information across multiple graphs to improve community detection and graph matching. However, this correlation also introduces new technical hurdles, as the estimation error from each individual graph impacts the overall accuracy. The paper focuses on algorithmic developments to address these challenges. Efficient algorithms for almost exact and exact graph matching are developed, showing strong theoretical guarantees in specific parameter regimes, overcoming previous limitations of computationally inefficient methods. Importantly, these graph matching algorithms directly translate into improved community recovery techniques, allowing for exact recovery in cases where it is information-theoretically impossible using a single graph. The analysis highlights the intricate interplay between the correlation strength, network sparsity, and the feasibility of exact recovery, providing key insights into the underlying fundamental limits.

Graph Matching

#

The concept of ‘Graph Matching’, central to the research paper, focuses on efficiently aligning nodes across two or more correlated graphs. The core challenge lies in recovering a latent matching—an unknown permutation that maps nodes between the graphs—especially within the context of Stochastic Block Models (SBMs), which represent networks with underlying community structures. The paper makes significant strides by developing an efficient algorithm to solve this computationally hard problem under specific conditions. The algorithm leverages subgraph counts, a powerful technique for extracting structural information from graphs, and it is particularly designed to handle the additional errors arising from estimating the community partitions. A key finding highlights the importance of the edge correlation parameter; the algorithm succeeds when the correlation exceeds a critical threshold, demonstrating a connection between the information-theoretic limits of graph matching and its computational feasibility. Moreover, the work explores the implications of successful graph matching for community detection, showing that graph matching with multiple graphs can enable exact community recovery even in scenarios where it’s information-theoretically impossible using a single graph.

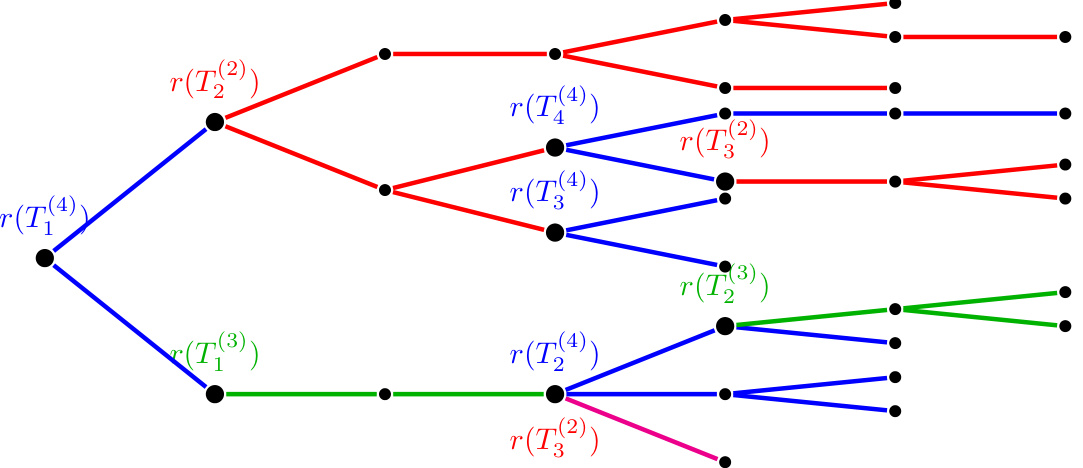
Chandelier Counts

#

The concept of “Chandelier Counts” in graph matching, as presented in the research paper, appears to be a novel approach using tree-like structures to efficiently compute informative features for node comparison. These structures, termed “chandeliers,” likely possess properties that facilitate the detection of true node correspondences amid noise and random variations in graph structures. The methodology centers on counting occurrences of specific chandelier subgraphs within the input graphs. These counts, potentially weighted or signed, serve as signature vectors for each node. The strength of this method rests on the discriminative power of the chosen chandelier set, which ideally allows efficient separation of the signature vectors for correctly matched nodes versus incorrectly matched ones. The algorithm’s efficiency hinges on a careful balance between the complexity of chandeliers (allowing for sufficiently rich node representations) and the computational cost of generating and comparing these signatures. Further analysis would likely involve examining the statistical properties of the chandelier counts (e.g., variance, concentration) under different random graph models. Finally, the effectiveness of the approach hinges on the choice of the specific chandelier set. This is a crucial step that likely requires careful theoretical analysis and might even benefit from machine learning techniques to optimize it for a particular graph family.

Community Recovery

#

The concept of community recovery, central to the study of correlated stochastic block models (correlated SBMs), involves reconstructing the latent community assignments of nodes given observed network data. The paper significantly advances this field by efficiently solving the graph matching problem in correlated SBMs under specific conditions on the correlation strength. This is crucial because accurate graph matching is often a prerequisite for successful community recovery, enabling the alignment of node labels between correlated graphs. The work highlights the interplay between community recovery and graph matching, showing that efficient graph matching algorithms can directly lead to efficient algorithms for community recovery. Importantly, the study demonstrates that by using multiple correlated graphs, exact community recovery is achievable in parameter regimes where it is information-theoretically impossible to achieve using only a single graph, thus demonstrating the power of correlated data in improving inference tasks. This is particularly relevant for real-world applications, where multiple correlated views or snapshots of a network might be available.

Future Research

#

The paper’s “Future Research” section would ideally explore several key areas. First, a deeper investigation into the tightness of the correlation threshold (s² > α) is crucial. Is this condition truly necessary, or could a more refined algorithm achieve exact graph matching under weaker correlation? Second, the algorithmic complexity warrants attention. The current polynomial-time algorithm could be improved to achieve near-optimal runtime. Third, generalization to more complex SBMs is essential. Extending the findings to scenarios with more than two communities, imbalanced communities, or differing community structures is a logical next step. Fourth, the interaction between graph matching and community detection requires further exploration. The current work uses community detection as a preliminary step, but more integrated approaches may yield significant improvements. Fifth, analyzing the impact of noise is essential. How robust is the algorithm to various types of noise and model misspecifications? Addressing these aspects would significantly enhance the impact and scope of the research.

More visual insights

#

More on figures

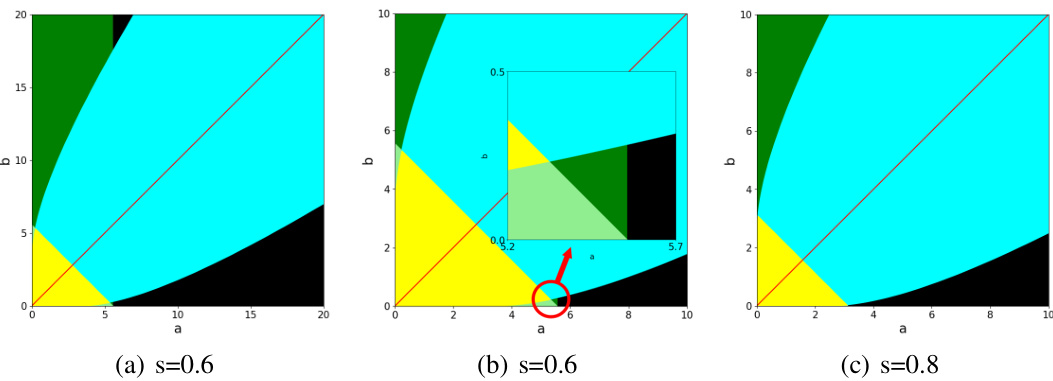
This phase diagram shows different regimes for graph matching in correlated stochastic block models (CSBMs) with two balanced communities, depending on the average degree (parameters a and b) and edge correlation (parameter s). Different colors represent different achievable levels of graph matching (exact or almost exact) and the algorithmic approaches used to achieve them. The diagram highlights the threshold for exact graph matching (s² > α) and illustrates how the algorithm generalizes existing approaches for Erdős-Rényi graphs.

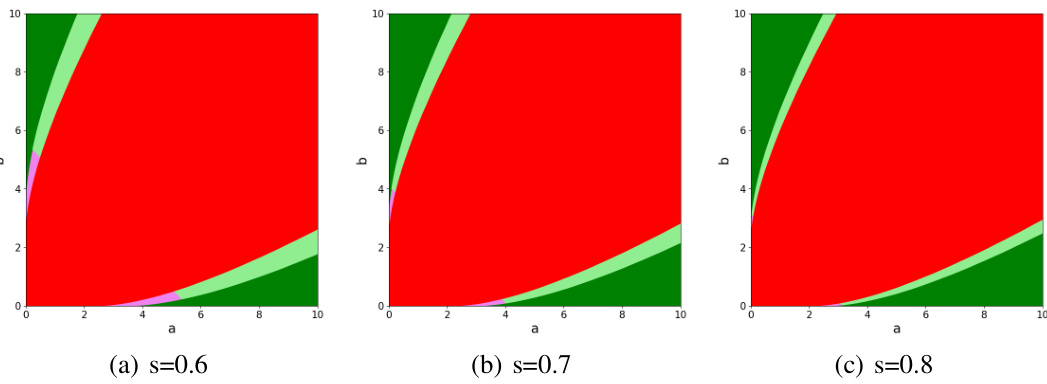
This phase diagram shows the different regimes of exact community recovery on correlated SBMs depending on the values of a, b and s. Green indicates that exact community recovery is possible using only a single graph. Light green indicates exact recovery is possible from both graphs but not a single graph. Violet indicates regions where exact recovery might be possible but the existence of efficient algorithms is unknown.

The figure schematically shows two correlated stochastic block models (SBMs) with two communities each. An SBM is a random graph where nodes belong to communities, and the probability of an edge between two nodes depends on their community memberships. In this figure, a parent SBM is generated first, with nodes assigned to communities (+1 or -1). Then, two child SBMs are generated by subsampling edges from the parent graph with probability s. The nodes in the two child SBMs are connected by a permutation π*, which represents the unknown node correspondence between the two graphs. This setup models the scenario where two graphs are correlated through a latent community structure and an unknown permutation.

The figure schematically illustrates the correlated stochastic block model (CSBM) with two communities. It shows a parent graph (G) generated from a standard SBM, which is then subsampled to create two correlated child graphs (G1 and G2). G1 inherits the community labels directly from G. G2 is also a subsample of G but has its vertices permuted by a random permutation (π*), which represents the unknown node alignment between the two graphs. This illustrates how the CSBM generates correlated graphs with a hidden matching.

This figure schematically illustrates the generation of two correlated stochastic block models (CSBMs) with two balanced communities. It starts with a parent graph generated from a standard stochastic block model, which has a latent community assignment for each node. Then two child graphs are created. In each child graph, each edge from the parent graph is included independently with probability s (the edge correlation parameter). One of these child graphs is then randomly permuted to obscure the correspondence between the nodes of the two graphs. The adjacency matrices of the two child graphs are then A and B.

The figure shows two correlated stochastic block models (SBMs) with two communities each. The top SBM (G) is the parent graph, with nodes colored to represent their community assignments. The edges are randomly generated with probabilities depending on community membership (p for same community, q for different communities). The two lower SBMs (G1 and G2) are generated by subsampling the edges of G (with probability s) independently for G1 and again for G2. Graph G2 has its nodes permuted according to a random permutation π* to simulate the unknown vertex alignment problem in real-world scenarios. This illustrates the generation of correlated SBMs, used as the basis for the study of graph matching.

This figure shows a schematic illustration of correlated stochastic block models (correlated SBMs) with two communities. It depicts the generation process of two correlated graphs (G1 and G2) from a parent graph G. The parent graph G is generated according to a stochastic block model with two balanced communities, where edges are formed based on the community memberships of nodes. Then, the two child graphs G1 and G2 are created by independently subsampling edges from G, introducing correlation between G1 and G2. Finally, a random permutation π* is applied to relabel the vertices of G2 to make the node correspondence between G1 and G2 unknown.

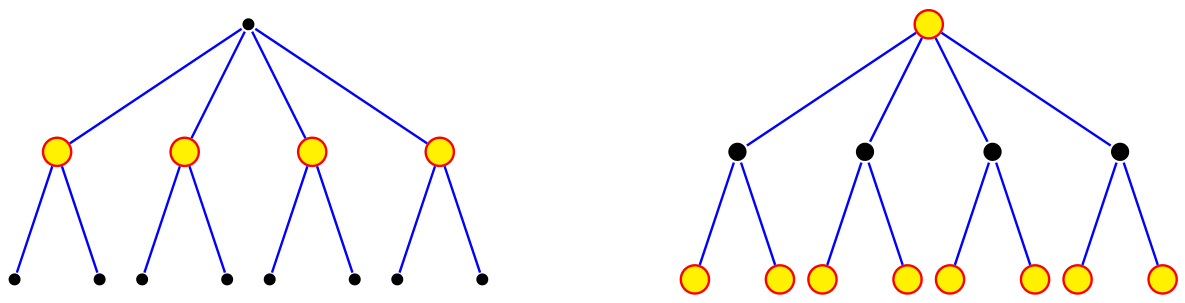
The figure shows a schematic of two correlated stochastic block models (SBMs) with two communities. An SBM is a random graph model where nodes belong to communities, and edges are more likely to connect nodes within the same community. In this figure, a parent graph G is generated first as an SBM. Then two child graphs, G1 and G2, are generated by subsampling edges from G independently. G2 is then permuted with a random permutation π* to model the unknown correspondence between the two graphs. This illustrates the concept of correlated SBMs, where the edge variables between the two graphs are correlated through their shared parent graph.

Full paper

#