Geometric Analysis of Nonlinear Manifold Clustering

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap between empirical success and theoretical understanding in nonlinear manifold clustering. Current state-of-the-art methods lack theoretical guarantees, hindering the field’s advancement. This research provides those guarantees and offers a novel, theoretically sound approach, opening doors for more robust and reliable manifold clustering techniques. It also demonstrates competitive empirical performance on benchmark datasets, bolstering the practical relevance of the theoretical advancements.

Visual Insights

#

This figure illustrates the concept of approximating a nonlinear manifold with an affine subspace. Point y is on manifold M1, and a ball B is drawn around it containing its nearest neighbors. The affine subspace S is constructed from the subset of these neighbors that also lie on M1 (x1 and x2). The figure shows that although the points x3 and x4 are close to y, they are on a different manifold (M2), highlighting the importance of considering manifold structure during clustering. The dashed circle represents the tangent circle used for curvature calculations (κ) at y.

This table compares the performance of the proposed methods L-WMC and E-WMC against other state-of-the-art methods for subspace clustering and deep clustering on CIFAR-10, CIFAR-20, and CIFAR-100 datasets. The results are presented using two metrics: Clustering Accuracy (ACC) and Normalized Mutual Information (NMI). The best result for each dataset and metric is highlighted in bold, while the best result achieved by the proposed methods is highlighted in blue. The table also separates methods into those that fine-tune representations and those that don’t, providing a more nuanced comparison.

In-depth insights

#

Nonlinear Manifold

#

Nonlinear manifold learning tackles the challenge of handling data that resides on complex, non-linear structures. Unlike linear methods that assume data points lie in a flat, Euclidean space, nonlinear manifold techniques recognize the curved, intrinsic geometry of high-dimensional data. These methods focus on preserving the local neighborhood relationships within the data’s manifold structure, a crucial aspect often lost in linear dimensionality reduction. The goal is to uncover the underlying lower-dimensional representation while maintaining the topological properties and global relationships. This involves utilizing techniques like kernel methods, graph embeddings, and neural networks to capture the data’s nonlinearity and embed it into a more manageable space, making tasks like clustering, classification, and visualization more effective. The success of nonlinear manifold learning depends on the quality of data sampling, the manifold’s smoothness, and the choice of appropriate algorithms. Furthermore, theoretical guarantees for these methods are often challenging to establish, creating a need for greater rigor and validation.

Geometric Analysis

#

A geometric analysis in a research paper would likely involve using geometric concepts and tools to understand and solve a problem. This could include analyzing shapes, distances, or other spatial relationships within data to identify patterns or structures. The approach might involve visualizing the data in a geometric space, perhaps using dimensionality reduction or manifold learning techniques, to reveal underlying relationships that are not apparent in the original high-dimensional space. For example, it could use techniques like principal component analysis or t-distributed stochastic neighbor embedding to project the data onto a lower-dimensional space while preserving important geometric properties. The goal would be to draw conclusions and create insights not otherwise possible through traditional statistical methods. Geometric analysis could reveal the presence of clusters, the topology of the data manifold, or the existence of certain geometric invariants, all of which could illuminate the underlying nature of the problem. This could significantly impact the interpretation of experimental results, or even lead to the development of new algorithms tailored to the specific geometric structures discovered. Key to a successful geometric analysis is the choice of appropriate geometric tools and the careful interpretation of the results in the context of the research question. It’s crucial that any conclusions drawn remain grounded in the mathematical framework and its limitations.

CIFAR Experiments

#

The CIFAR experiments section likely evaluates the proposed manifold clustering method against state-of-the-art techniques on the CIFAR-10, -20, and -100 datasets. The focus is likely on demonstrating competitive performance, comparing the method’s accuracy and normalized mutual information (NMI) scores with those of other subspace clustering methods and deep learning-based approaches. A key aspect is the comparison of methods with and without theoretical guarantees, highlighting the trade-off between empirical performance and theoretical rigor. The results would show whether the proposed method’s theoretical foundation translates to competitive results on a widely used benchmark. Detailed analysis of the results would likely include discussion of the effect of hyperparameters, particularly the regularization parameter (lambda) and the homogenization constant (eta), on the method’s performance and robustness. It would also delve into any observed strengths or weaknesses, perhaps highlighting situations where the model particularly excels or falls short.

Theoretical Guarantees

#

The research paper delves into the crucial aspect of providing theoretical guarantees for nonlinear manifold clustering, a significant challenge in data science. Existing state-of-the-art methods often lack theoretical justification, despite exhibiting good empirical performance. This paper directly addresses this gap by introducing a novel clustering method and rigorously proving its correctness under specific geometric conditions. These conditions relate to the sampling density of the manifolds, their curvature, and the separation between different manifolds. The theoretical analysis is a major contribution, offering a deeper understanding of the underlying mechanisms at play. The theoretical guarantees provide confidence that the proposed method reliably recovers manifold structure during clustering, which is not guaranteed by many empirical methods. However, it is important to note that the theoretical guarantees come with assumptions about data distribution and manifold properties, which might not always hold in real-world datasets. Therefore, a balance between theoretical soundness and practical applicability is crucial; this is addressed by the paper through empirical evaluations demonstrating competitive performance compared to established methods on real-world datasets.

Future Directions

#

Future research could explore relaxing the strict geometric assumptions of the current model to handle more complex datasets. Investigating alternative regularizers beyond the ℓ₁ norm could lead to improved performance and robustness. A key area for development lies in developing more efficient algorithms to address the computational challenges of clustering large-scale datasets. Theoretical analysis could be further refined to provide tighter bounds and more practical guidelines for hyperparameter selection. Finally, extending the framework to handle various data modalities and incorporate uncertainty would greatly broaden the applicability of the proposed manifold clustering method.

More visual insights

#

More on figures

This figure shows the results of an experiment evaluating how the values of λ¹ and λ² (defined in Lemma 1 of the paper) change as a function of the hyperparameter λ. Four subplots show the relationship between λ¹, λ², and λ for different numbers of data samples (N₁, N₂) from two trefoil knots. The data points are embedded in a 100-dimensional space using 50 different random orthonormal bases. The plots show the mean values and standard deviations of λ¹ and λ² for different values of λ. The results are used to demonstrate how the conditions in Lemma 1 of the paper are satisfied.

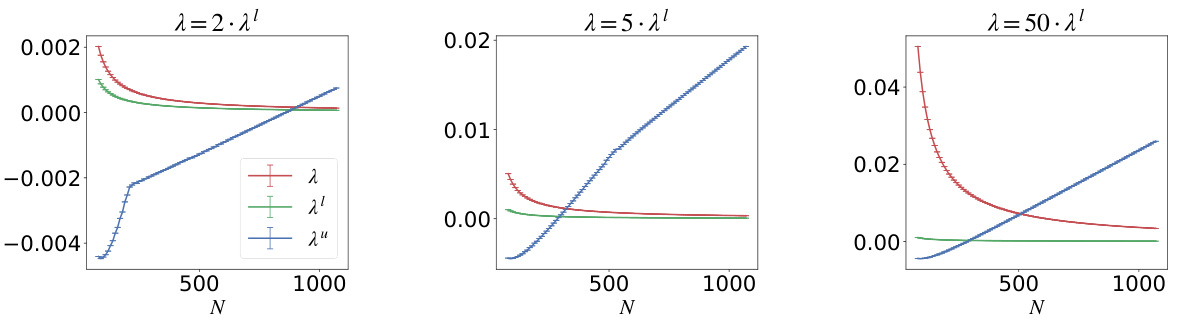
This figure shows how the values of λ¹ and λ² (defined in Lemma 1 of the paper) change as a function of the number of data samples N, and the hyperparameter λ, for data generated from two trefoil knots. Three different values for λ are used (λ = aλ¹ where a = 2, 5, 50). The plots show the mean values and standard deviations of λ¹ and λ² calculated from 50 different random embeddings of the data. The plot shows that for N₁=120, 150, the conditions in Lemma 1(a) are not satisfied for any value of λ. For N₁=160, 200, and for some values of λ > 0, there exist non-empty intervals (λ¹, λ²) such that λ ∈ (λ¹, λ²). In this case, Lemma 1 states that every optimal solution to (WMC) is manifold preserving and nonzero.

More on tables

This table compares the performance of the proposed manifold clustering methods (L-WMC and E-WMC) against several state-of-the-art subspace and deep clustering methods on three CIFAR datasets (CIFAR-10, CIFAR-20, and CIFAR-100). The table reports clustering accuracy (ACC) and Normalized Mutual Information (NMI), two common metrics for evaluating clustering performance. The methods are categorized into those that do and do not fine-tune their representations. The best results for each dataset and metric are highlighted in bold, with the best results obtained by the proposed methods shown in blue.

This table compares the performance of the proposed methods (L-WMC and E-WMC) against other state-of-the-art subspace and deep clustering methods on CIFAR-10, CIFAR-20, and CIFAR-100 datasets. The results are presented in terms of clustering accuracy (ACC) and Normalized Mutual Information (NMI). The best overall performance for each metric and dataset is highlighted in bold, and the best performance achieved by the proposed methods is indicated in blue. The table is divided into two sections: methods that do not fine-tune representations and methods that do fine-tune representations.

This table compares the performance of the proposed manifold clustering methods (L-WMC and E-WMC) against several state-of-the-art subspace and deep clustering methods on three CIFAR datasets (CIFAR-10, CIFAR-20, CIFAR-100). The comparison uses two metrics: Clustering Accuracy (ACC) and Normalized Mutual Information (NMI). The best result for each dataset and metric is highlighted in bold, while the best result achieved by the proposed methods is highlighted in blue. The table is further divided into methods that do and do not fine-tune representations.

This table compares the performance of the proposed L-WMC and E-WMC models against several state-of-the-art subspace and deep clustering methods. The comparison is done using two metrics: Clustering Accuracy (ACC) and Normalized Mutual Information (NMI), for three different CIFAR datasets (CIFAR-10, CIFAR-20, and CIFAR-100). The best overall performance for each metric and dataset is highlighted in bold, while the best performance achieved by the proposed methods is highlighted in blue. The data used for all methods was pre-trained using CLIP.

Full paper

#