↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Latent Diffusion Models (LDMs) are powerful generative models, but accurately inverting their decoder to map pixel-space to latent-space remains challenging. Existing gradient-based methods are computationally expensive and memory-intensive, particularly for high-dimensional latent spaces such as those found in video LDMs. This significantly limits their applicability in tasks that require precise decoder inversion.
This research proposes a novel gradient-free decoder inversion method. This approach is faster and more memory-efficient, making decoder inversion practical for a wider range of applications and higher-dimensional LDMs. The method’s theoretical convergence is proven, and it achieves comparable accuracy while drastically reducing computation time and memory usage in experiments involving various LDMs.
Key Takeaways#
Why does it matter?#
This paper is highly important for researchers working on latent diffusion models and deep generative models because it presents a novel gradient-free method for efficient and memory-friendly decoder inversion. This addresses a critical limitation of existing methods, which often struggle with larger latent spaces. The work also opens new avenues for research in various applications such as noise-space watermarking and background-preserving image editing.
Visual Insights#
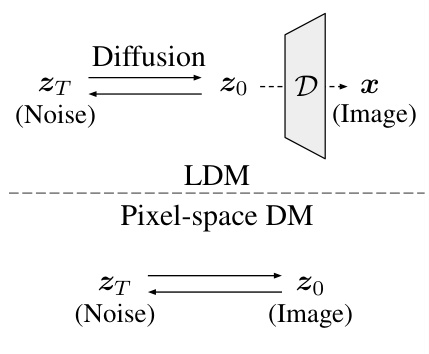
The figure compares Latent Diffusion Models (LDMs) and pixel-space Diffusion Models (DMs). It highlights how LDMs utilize a decoder to map latent representations to pixel space, unlike pixel-space DMs. The figure contrasts the invertibility of different generative models, emphasizing the computational cost and memory requirements of gradient-based inversion methods for LDMs and the advantages of the proposed gradient-free method. The left subfigure shows how latent diffusion models (LDMs) use a decoder to map the low-dimensional latent space to pixel space, while pixel-space DMs operate directly in pixel space. The right subfigure illustrates the difference in the invertibility of various generative models and positions the proposed gradient-free method.

This table compares various deep generative models (GANs, NFs, and DMs) based on three key aspects of generative learning: high-quality samples, diversity, and fast sampling. It highlights that while Diffusion Models (DMs) have solved the generative learning trilemma, they still lack the invertibility property compared to other models. Latent Diffusion Models (LDMs), a specific type of DM, require additional decoder inversion, which has traditionally been computationally expensive. The paper proposes a new efficient, gradient-free method to address this limitation in LDMs.
In-depth insights#
Grad-Free Inversion#
The concept of ‘Grad-Free Inversion’ in the context of latent diffusion models presents a compelling alternative to traditional gradient-based methods. Gradient-free approaches offer significant advantages in terms of computational efficiency and memory usage, especially crucial when dealing with high-dimensional latent spaces common in advanced LDMs. By eliminating the need for computationally expensive gradient calculations, these methods enable faster and more memory-efficient decoder inversion, making them highly suitable for applications involving large-scale models or real-time processing. The theoretical grounding of convergence properties for both forward-step and inertial KM iteration methods adds robustness to the approach, suggesting that even without the explicit guidance of gradients, the inversion process can still converge effectively under certain conditions. The practical implications are substantial, opening doors for real-world applications such as noise-space watermarking and background-preserving image editing that were previously limited by the computational constraints of gradient-based methods. However, it’s important to acknowledge the trade-offs; while gradient-free methods offer efficiency gains, they might sacrifice some degree of accuracy compared to their gradient-based counterparts. Therefore, the choice between gradient-free and gradient-based inversion techniques should be driven by the specific application requirements and the balance between speed, memory efficiency, and precision.
LDM Invertibility#
LDM invertibility, the ability to recover a latent representation from a generated image, is a critical challenge in latent diffusion models (LDMs). Unlike invertible models like normalizing flows, LDMs employ a forward diffusion process, making direct inversion difficult. Existing methods often rely on gradient-based optimization, which is computationally expensive and memory-intensive, particularly for high-resolution images and video LDMs. This limitation hinders applications requiring precise inversion, such as image editing and watermarking. The paper addresses this by proposing a gradient-free inversion method. This approach offers significant advantages in terms of speed and memory efficiency. The method’s theoretical convergence properties are analyzed, demonstrating its effectiveness under mild assumptions. Importantly, this gradient-free approach enables efficient computation in scenarios where gradient-based methods are impractical, thus broadening the applicability of LDMs. The authors validate the approach through experiments on various LDMs, including image and video models. These results show significant improvements over existing methods, paving the way for more efficient and versatile applications of LDMs.
Convergence Analysis#
A rigorous convergence analysis is crucial for establishing the reliability and effectiveness of any iterative algorithm. In the context of decoder inversion for latent diffusion models, a thorough analysis is needed to demonstrate that the proposed gradient-free method reliably converges to the true solution, especially given the inherent challenges of decoder inversion. This analysis should ideally include a formal proof of convergence under specific conditions, such as assumptions about the properties of the encoder and decoder, and the characteristics of the optimization process. The analysis should also consider the impact of different parameters, such as step size or momentum, on the convergence rate. A comparison of the convergence properties of the gradient-free method with existing gradient-based methods is important, highlighting any advantages or disadvantages in terms of speed, accuracy, and memory efficiency. Furthermore, empirical validation of the theoretical analysis through extensive experiments is essential. These experiments should explore a range of latent diffusion models, datasets, and inversion scenarios to demonstrate the generalizability of the convergence results. The analysis must also address the robustness of the method to noise and other potential sources of error, thereby providing a solid foundation for the practical application of the gradient-free decoder inversion technique.
Practical Optimizers#
A section on ‘Practical Optimizers’ within a research paper would likely delve into the implementation details of optimization algorithms beyond theoretical analysis. It would discuss choices like Adam or variations thereof, focusing on aspects such as learning rate scheduling, momentum strategies, and hyperparameter tuning. The discussion would likely analyze the trade-offs between computational efficiency, memory usage, and convergence speed for different optimizer configurations. Practical considerations, such as handling numerical instability or adapting to specific hardware limitations, would also be key. The authors might present experimental results demonstrating the performance of various optimizers in the context of the paper’s specific task, possibly comparing them against baseline methods. A strong emphasis would be placed on reproducibility, providing details that allow others to replicate the results accurately.
Applicability of LDMs#
Latent Diffusion Models (LDMs) demonstrate significant potential across diverse applications. Image generation is a primary strength, producing high-quality, diverse outputs. LDMs also excel in image editing, offering nuanced control while preserving essential features like backgrounds. Video generation is emerging as another promising area, with LDMs showing aptitude for creating coherent and visually appealing sequences. Beyond visual domains, the adaptability of LDMs suggests potential in areas such as audio synthesis and even molecular structure design. However, challenges remain, particularly concerning invertibility, the ability to accurately recover the latent representation from a generated image or video; this remains a critical area for future research and development to fully unlock the potential of LDMs across an even wider array of applications. Scalability is another key factor; computationally intensive techniques can hinder widespread usage, thus efficient methods are crucial for wider adoption.
More visual insights#
More on figures
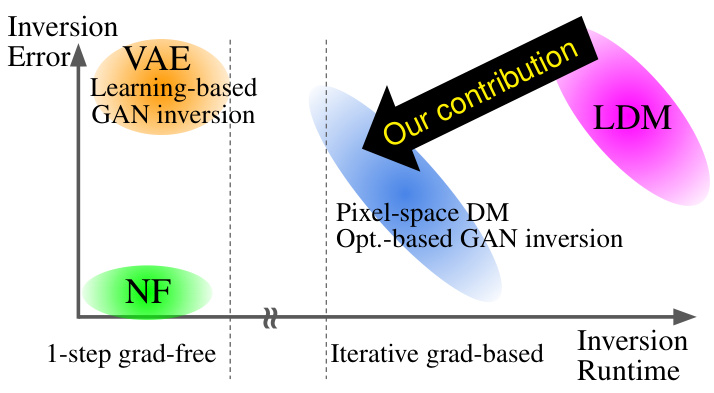
This figure compares different generative models based on their invertibility and computational cost. (a) illustrates the difference between Latent Diffusion Models (LDMs) and pixel-space Diffusion Models, highlighting the role of the decoder. (b) positions various models along two axes: inversion runtime (x-axis) and inversion error (y-axis). It shows that LDMs, due to their latent space representation, present a greater challenge for decoder inversion compared to pixel-space models. The authors’ proposed gradient-free method is presented as an efficient solution that improves inversion for LDMs.
This figure compares latent diffusion models (LDMs) with pixel-space diffusion models in terms of invertibility. (a) illustrates the core difference: LDMs use a decoder to map latent representations to pixel space, while pixel-space models work directly in pixel space. (b) shows that the introduction of the decoder in LDMs, while efficient for generation, makes inversion more challenging, particularly with gradient-based methods. The authors’ proposed gradient-free method addresses this challenge by directly handling the latent-to-pixel space mapping.

This figure illustrates the core difference between Latent Diffusion Models (LDMs) and pixel-space Diffusion Models, highlighting the role of the decoder in the inversion process. Panel (a) shows the architecture difference, emphasizing how LDMs utilize a latent space, while (b) visualizes the trade-off between speed and accuracy for different inversion methods, showcasing the advantage of the proposed gradient-free approach for LDMs.

This figure illustrates the core difference between Latent Diffusion Models (LDMs) and pixel-space Diffusion Models (DMs) in terms of invertibility. (a) shows that LDMs utilize a decoder to map from latent space to pixel space, unlike pixel-space DMs which operate directly in pixel space. (b) highlights that while pixel-space DMs and gradient-based GAN inversion methods rely on iterative gradient descent, making them computationally expensive, the proposed gradient-free decoder inversion method offers a more efficient alternative for LDMs, especially beneficial when dealing with the lossy nature of latent representations in LDMs.

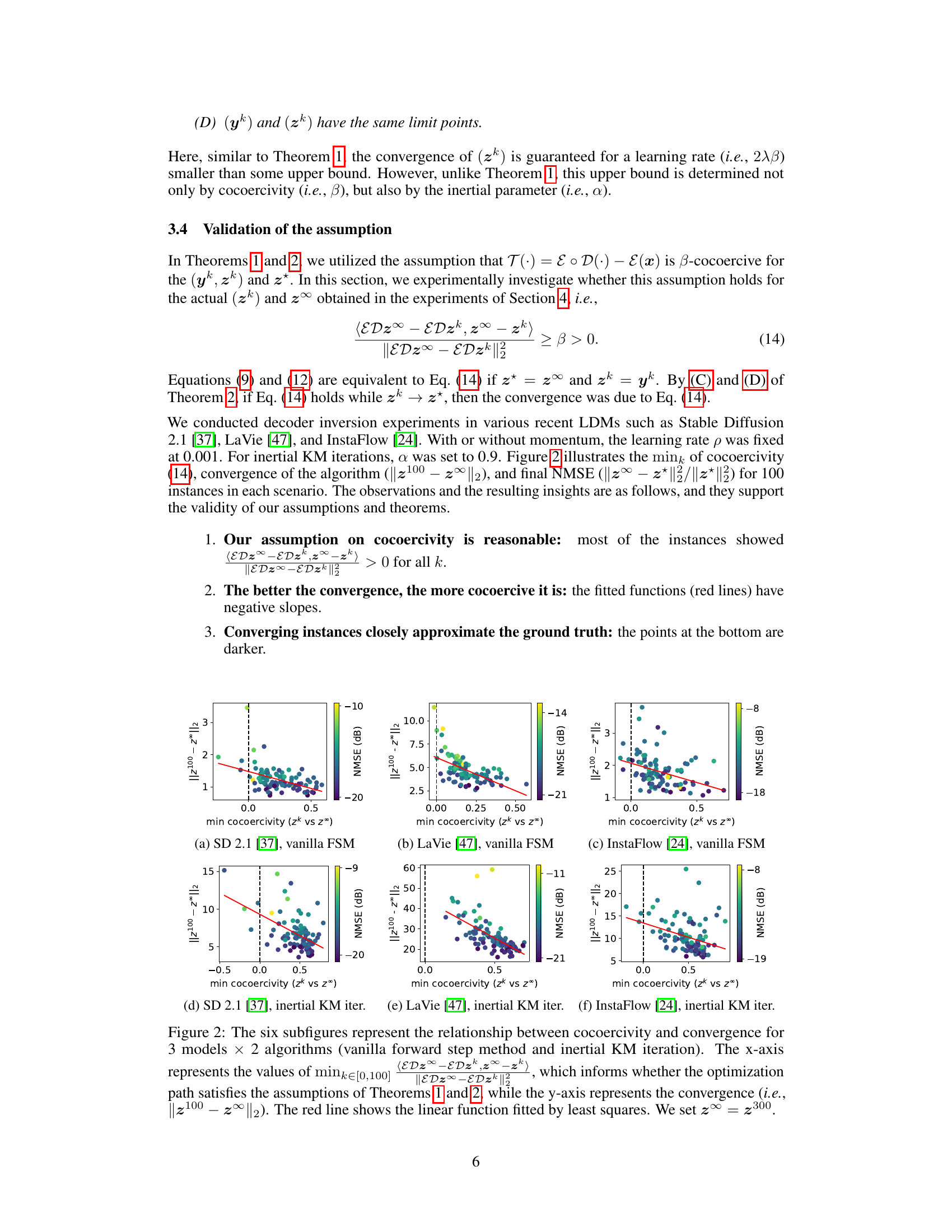
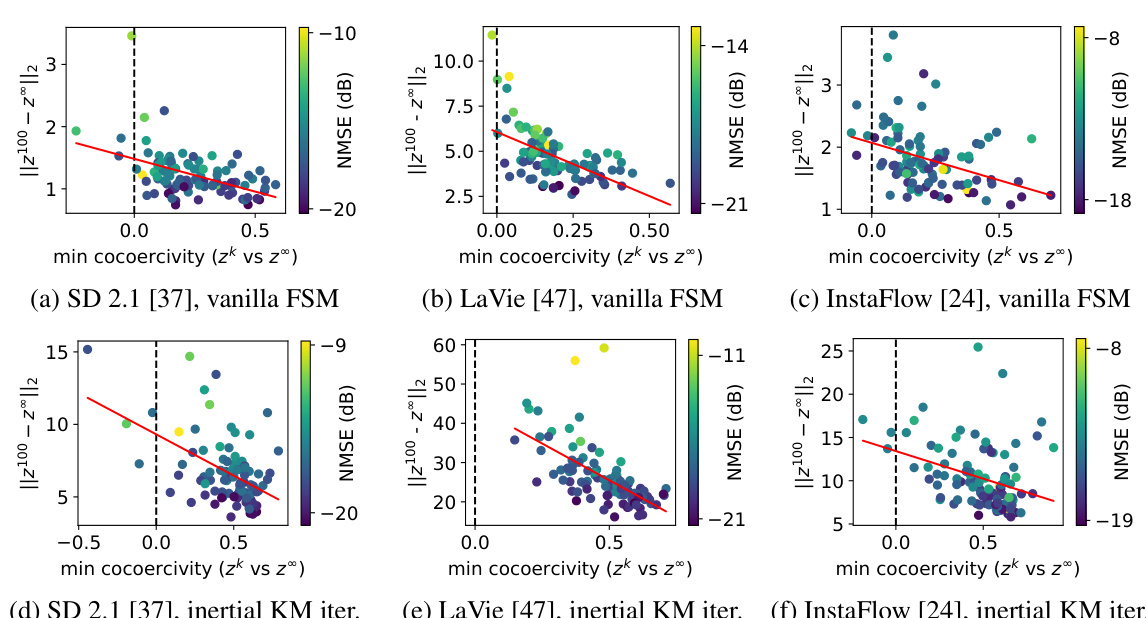
This figure shows the relationship between cocoercivity and convergence for three different latent diffusion models using two different algorithms: the vanilla forward step method and the inertial KM iteration. The x-axis represents the minimum cocoercivity, indicating how well the conditions of Theorems 1 and 2 are met. The y-axis represents convergence speed. Each point represents results from a single instance within the given model and algorithm.
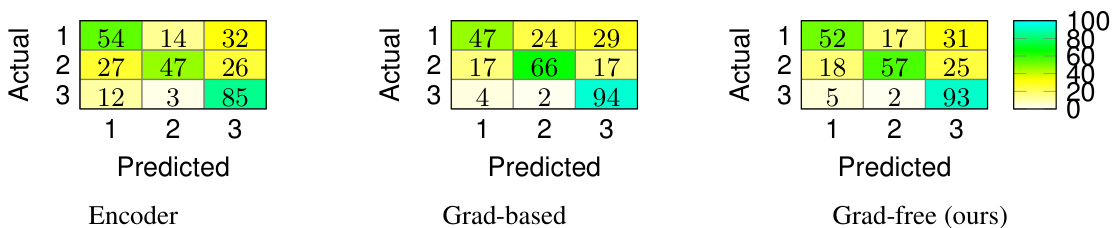
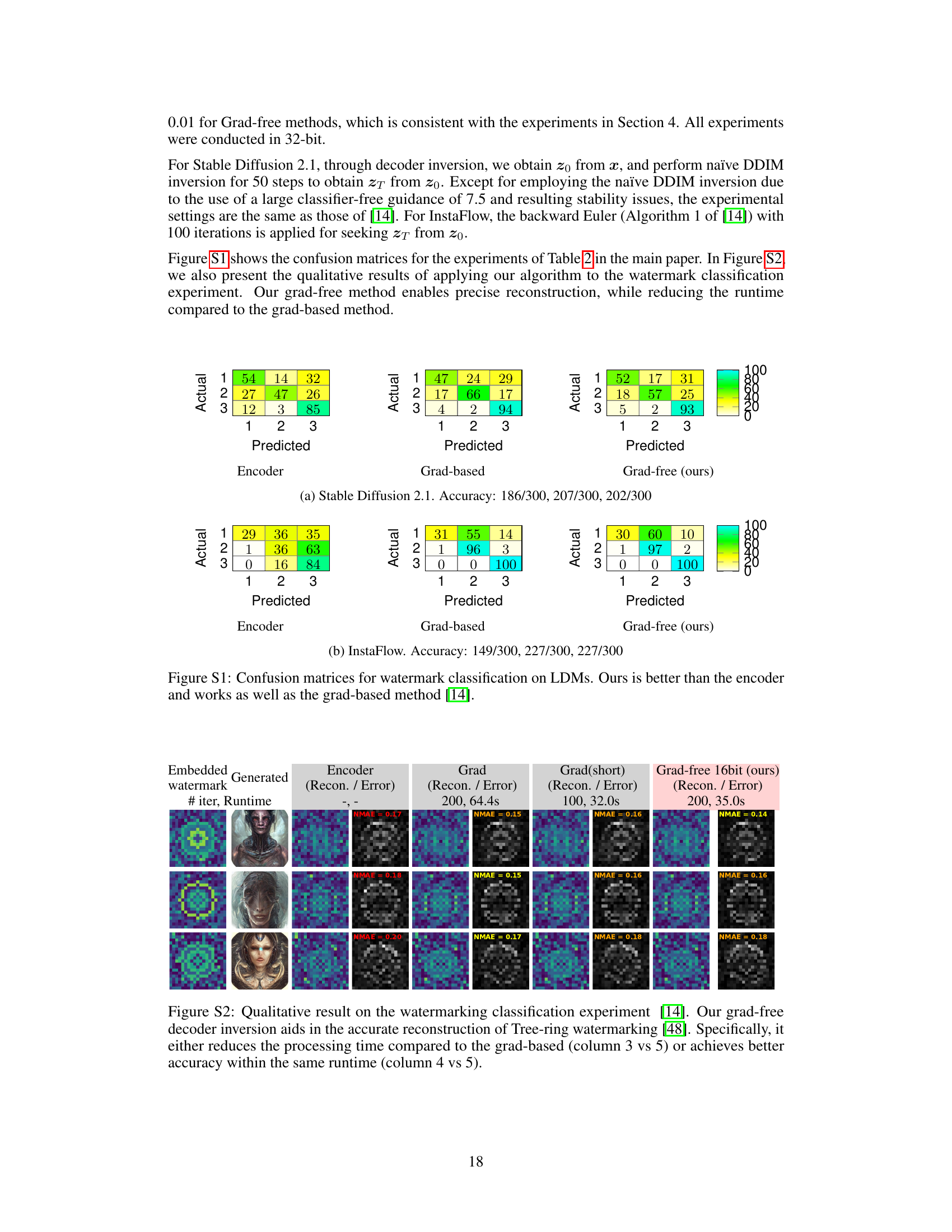
This figure shows three confusion matrices, one for each of the three methods used for watermark classification: Encoder, Grad-based, and Grad-free (ours). Each matrix displays the number of correctly and incorrectly classified images for three different watermark types. The Grad-free method achieves comparable performance to the Grad-based method but outperforms the Encoder method.

This figure presents the confusion matrices for watermark classification experiments using three different methods: Encoder, Gradient-based, and the proposed Gradient-free method. Each confusion matrix shows the performance of each method in classifying three different tree-ring watermarks (represented by classes 1, 2, and 3). The results indicate that the Gradient-free method achieves comparable accuracy to the Gradient-based method, and significantly outperforms the Encoder method.
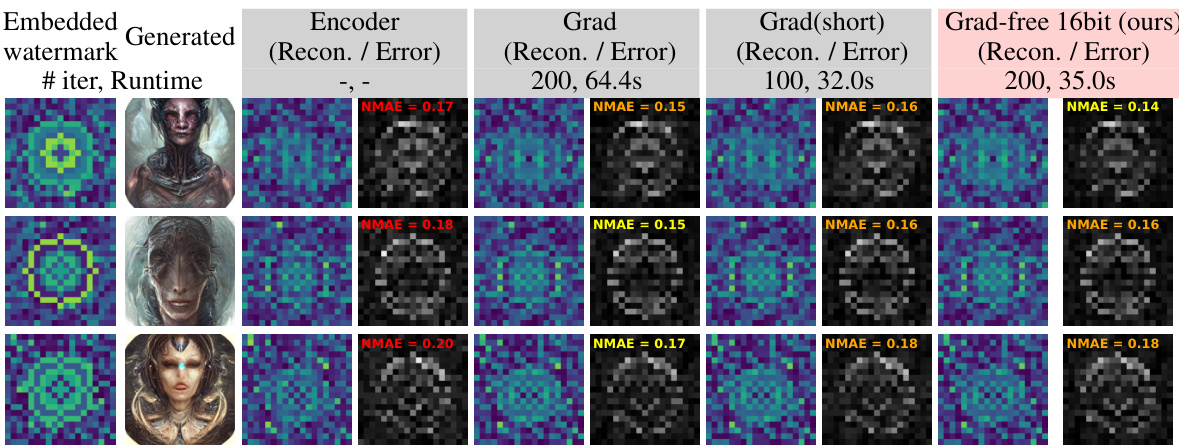
This figure shows a qualitative comparison of watermark classification results using different methods: encoder, gradient-based method, shortened gradient-based method, and the proposed gradient-free method. It demonstrates that the gradient-free method achieves comparable or better accuracy with significantly reduced runtime compared to the gradient-based methods.
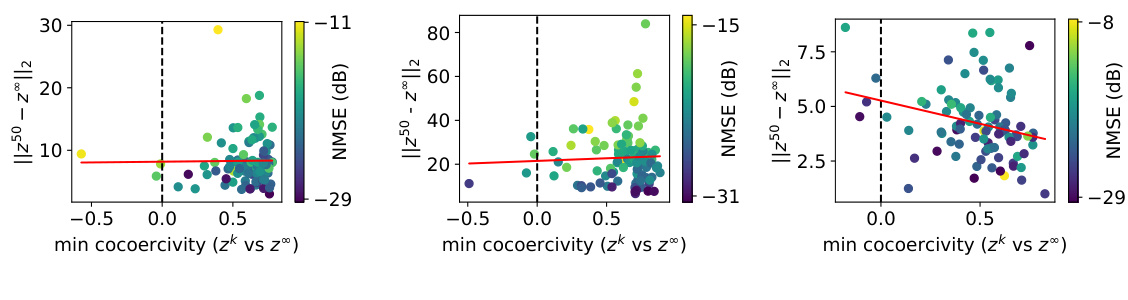
This figure shows the relationship between cocoercivity and convergence for three different latent diffusion models using two different algorithms (vanilla forward step method and inertial KM iteration). The x-axis represents the minimum cocoercivity value across iterations, indicating whether the optimization process satisfies certain assumptions. The y-axis shows the convergence rate, represented by the distance between the final latent vector and the ground truth. The red line shows a linear fit, helping visualize the overall trend.
More on tables
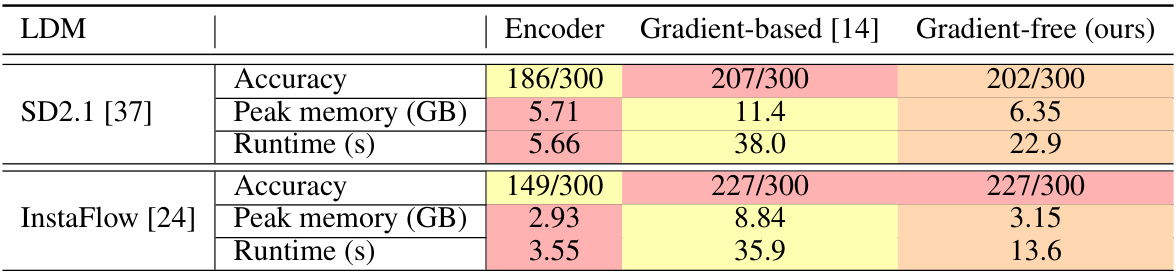
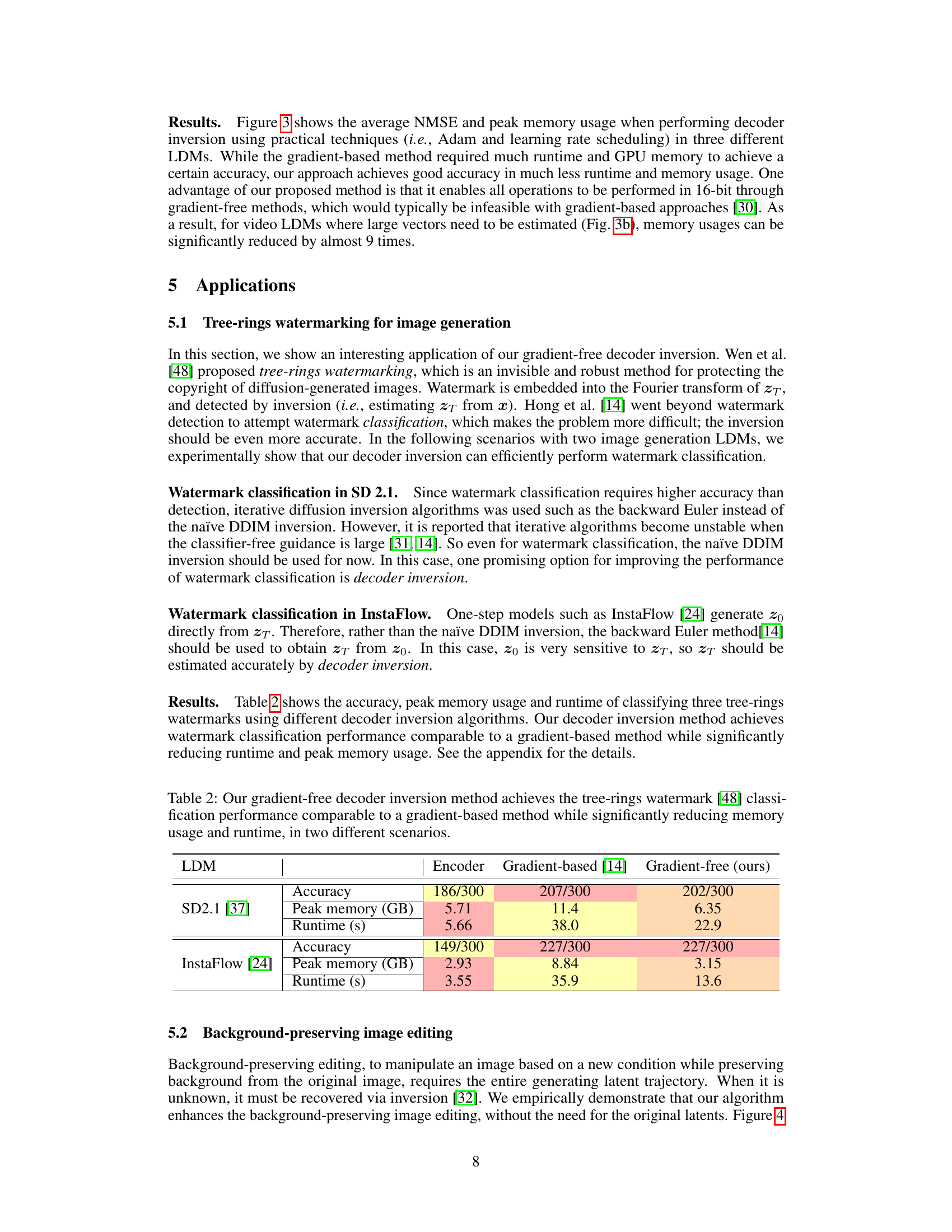
This table presents a comparison of the performance of three different decoder inversion methods: Encoder, Gradient-based, and Gradient-free (ours) on two different Latent Diffusion Models (LDMs): Stable Diffusion 2.1 and InstaFlow. The metrics compared are Accuracy, Peak memory usage (GB), and runtime (s). The results show that the proposed Gradient-free method achieves comparable accuracy to the Gradient-based method while significantly reducing both memory usage and runtime.

This table compares several deep generative models (GAN, NF, and DM) based on three criteria of the generative learning trilemma (high-quality samples, diversity, and fast sampling) and their invertibility. It highlights that while Diffusion Models (DMs) have solved the trilemma, they lack invertibility, especially Latent Diffusion Models (LDMs), which necessitate a decoder inversion process. The authors propose a gradient-free method to efficiently address the invertibility issue in LDMs.

This table presents the results of decoder inversion experiments conducted on three different latent diffusion models (LDMs): Stable Diffusion 2.1, LaVie, and InstaFlow. The experiments compare the performance of a gradient-based method and a gradient-free method proposed in the paper. Different hyperparameters were tested, including different learning rates (0.1 scheduled and 0.01 fixed) and number of iterations (20, 30, 50, 100, 200). The table shows NMSE (Noise reconstruction Mean Squared Error) in dB, number of iterations, runtime in seconds, and peak GPU memory usage in GB for each experiment. The ± values indicate the 95% confidence intervals.

This table compares the performance of three different decoder inversion methods (Encoder, Gradient-based [14], and Gradient-free (ours)) for tree-rings watermark classification in two different Latent Diffusion Models (LDMs). The metrics compared are accuracy, peak memory usage (in GB), and runtime (in seconds). The results demonstrate that the gradient-free method achieves comparable accuracy to the gradient-based method while significantly reducing both memory usage and runtime.
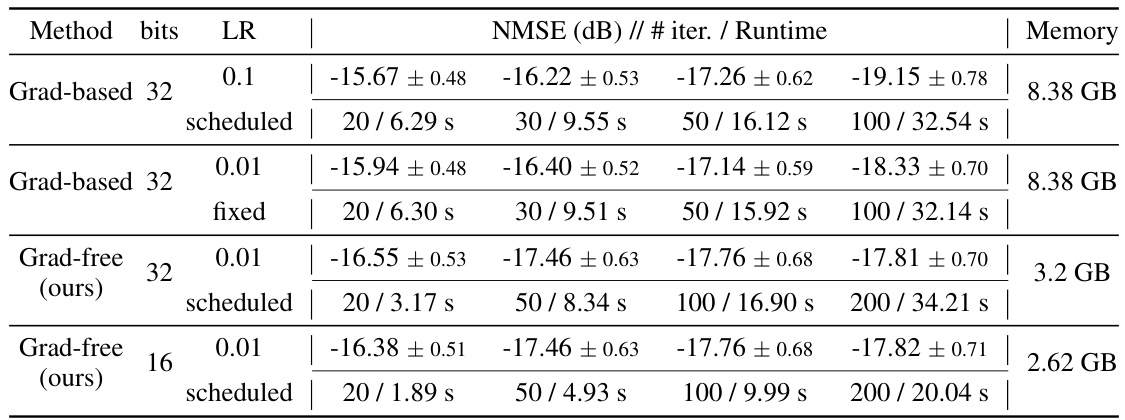
This table presents the results of decoder inversion experiments conducted on three different latent diffusion models (LDMs): Stable Diffusion 2.1, LaVie, and InstaFlow. The experiments compare the performance of gradient-based and gradient-free decoder inversion methods using different bit precisions (16-bit and 32-bit), learning rates (fixed and scheduled), and numbers of iterations. The metrics reported include NMSE (noise reconstruction mean squared error), the number of iterations, runtime, and peak GPU memory usage. The table provides a detailed comparison to highlight the efficiency gains achieved by the proposed gradient-free method, particularly in terms of reduced memory consumption and runtime, while maintaining comparable accuracy.
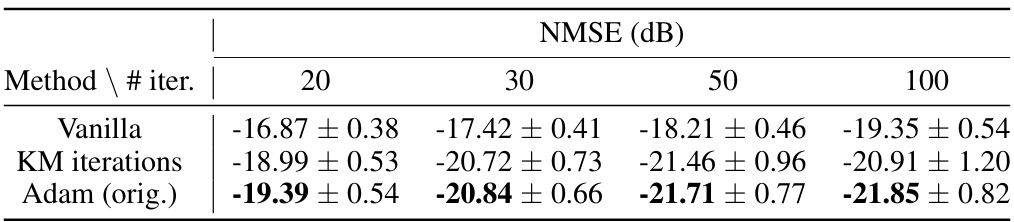
This table presents the results of ablation studies conducted to evaluate the impact of different optimizers (Vanilla, KM iterations, Adam) and learning rate scheduling strategies on the performance of the decoder inversion method. The experiment was performed with varying numbers of iterations (20, 30, 50, 100). The results, measured by NMSE (dB), show that the Adam optimizer consistently outperforms the other methods across all iteration counts, and the learning rate scheduling strategy employed yielded consistently good results across different iteration numbers.
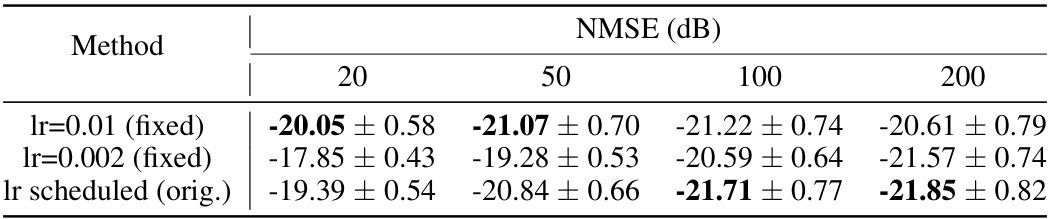
This table presents the results of ablation studies conducted to evaluate the impact of different optimizers (vanilla, KM iterations, Adam) and learning rate scheduling methods on the performance of the decoder inversion. The results, measured in NMSE (dB), are shown for different numbers of iterations (20, 30, 50, 100). The study demonstrates that the Adam optimizer with the original learning rate scheduling achieves the best performance across all iteration counts.
Full paper#