TL;DR#
Many real-world applications involve comparing entities based on multiple criteria. Existing methods often fail to consider the dependencies between these criteria, leading to unreliable rankings. This paper focuses on multivariate stochastic dominance, a statistical framework for robustly comparing such entities. The challenge is that directly applying multivariate stochastic dominance is computationally expensive and difficult.
This research proposes a novel method using optimal transport, a mathematical concept for comparing probability distributions. By introducing entropic regularization, the authors address the computational challenges. They prove a central limit theorem and consistency of the bootstrap procedure for their statistic, allowing statistically significant comparisons. This enhanced framework significantly improves the robustness and efficiency of multi-criteria comparisons, especially beneficial in evaluating large language models across numerous metrics.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in machine learning and statistics because it provides a novel framework for comparing models based on multiple performance metrics. It offers a statistically sound method that considers dependencies between metrics, enhancing the robustness of model selection. This approach is highly relevant to the current trend of large-language model (LLM) benchmarking, where multiple evaluation metrics are often used. The efficient implementation using the Sinkhorn algorithm makes the method practical for real-world applications, opening new avenues for statistical analysis within the field of multivariate stochastic dominance.
Visual Insights#

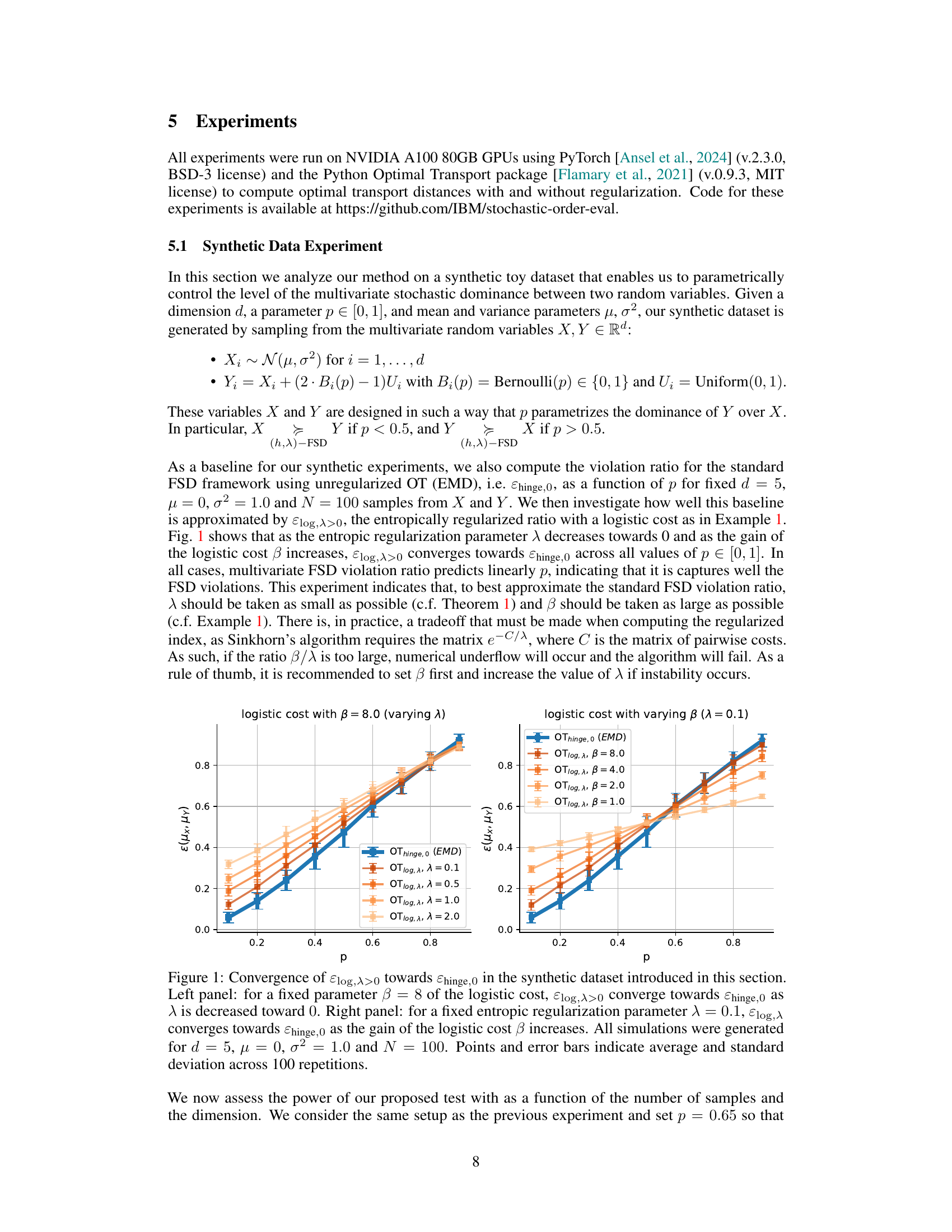
🔼 This figure shows the convergence of the entropic regularized violation ratio (εlog,λ) towards the unregularized one (εhinge,0) as a function of the entropic regularization parameter (λ) and the gain of the logistic cost (β). The left panel shows convergence with varying λ and fixed β, while the right panel illustrates convergence with varying β and fixed λ. The results demonstrate that as λ approaches 0 and β increases, the regularized ratio closely approximates the unregularized ratio.
read the caption
Figure 1: Convergence of εlog,λ>0 towards εhinge,0 in the synthetic dataset introduced in this section. Left panel: for a fixed parameter β = 8 of the logistic cost, εlog,λ>0 converge towards εhinge,0 as λ is decreased toward 0. Right panel: for a fixed entropic regularization parameter λ = 0.1, εlog,λ converges towards εhinge,0 as the gain of the logistic cost β increases. All simulations were generated for d = 5, μ = 0, σ² = 1.0 and N = 100. Points and error bars indicate average and standard deviation across 100 repetitions.
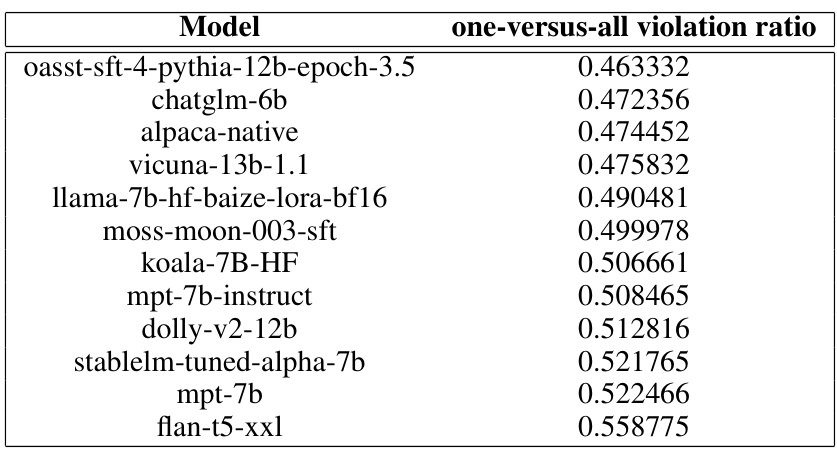
🔼 This table presents the ranking of 12 large language models (LLMs) based on their one-versus-all violation ratios. The ranking is determined using the entropic multivariate first-order stochastic dominance (FSD) test described in the paper. A lower violation ratio indicates a more dominant model, suggesting better overall performance across multiple evaluation metrics. The sample size (n) used for the ranking is 5000.
read the caption
Figure 4: This table ranks the 12 models tested in the LLM benchmarking experiment using n = 5000 samples according to their one-versus-all violation ratio, ε(h,λ)i(M) = Σj≠i ε(h,λ)ij, where ε(h,λ)ij is the pairwise violation ration of model i compared with model j (lower is better).
In-depth insights#
Multi-metric Benchmarking#
Multi-metric benchmarking in large language models (LLMs) presents a significant challenge due to the inherent complexities of evaluating performance across diverse tasks. Traditional approaches often rely on aggregating multiple metrics into a single score, losing valuable information about the nuanced strengths and weaknesses of each model. This simplification masks the intricate relationships between metrics, leading to potentially misleading conclusions about model ranking and relative performance. A more robust method is needed to assess multivariate model performance holistically. The optimal transport (OT) framework offers a powerful tool to directly compare the joint distributions of multiple LLM evaluation metrics. By capturing dependencies between metrics, OT-based benchmarking allows for a more fine-grained and accurate understanding of model capabilities, enabling a more informed decision-making process for selecting the most suitable model for a given application. Future research should explore extending OT methods to incorporate diverse evaluation scenarios, including non-numeric metrics and user preferences. Furthermore, investigating the impact of various cost functions on the resulting rankings and addressing the computational challenges of OT in high-dimensional settings are crucial for realizing the full potential of this promising benchmarking strategy.
Entropic OT Approach#
The Entropic OT approach presents a powerful technique for addressing the challenges inherent in multivariate stochastic dominance testing. By incorporating entropic regularization into the optimal transport framework, it mitigates the computational complexity associated with high-dimensional data. This regularization allows for efficient computation of the entropic multivariate FSD violation ratio, a crucial statistic for assessing almost stochastic dominance. The method’s robustness is further enhanced by its ability to capture dependencies between multiple metrics, a significant advantage over techniques relying on univariate reductions. The accompanying central limit theorem and consistent bootstrap procedure provide a strong foundation for hypothesis testing, enabling statistically rigorous comparisons. The algorithm’s efficiency is showcased through its application to large language model benchmarking, where multivariate evaluations are increasingly common. While the use of the Sinkhorn algorithm for efficient computation is a noteworthy feature, it is important to acknowledge the reliance on specific assumptions, such as the sub-Gaussianity of the data. Future work might focus on expanding the framework to handle diverse cost functions and to explore alternative regularization strategies. Nonetheless, the presented approach offers a significant contribution to the field of multivariate stochastic dominance, providing a practical and statistically sound method for comparing complex systems with multiple performance indicators.
CLT and Bootstrap#
The section on ‘CLT and Bootstrap’ is crucial for establishing the statistical validity of the proposed multivariate almost stochastic dominance test. The Central Limit Theorem (CLT) provides the foundation, demonstrating that the empirical estimator of the multivariate violation ratio converges to a normal distribution as the sample size increases. This asymptotic normality is essential for constructing hypothesis tests and confidence intervals. The bootstrap procedure complements the CLT by offering a practical way to estimate the variance of the empirical statistic, even when the theoretical variance is complex to calculate. The combination of the CLT and bootstrap provides a robust and efficient framework for statistical inference, enabling researchers to draw meaningful conclusions from the data about the relative performance of different models. The authors’ rigorous proof of these results significantly strengthens the credibility of the proposed method and its applications.
Hypothesis Testing#
The hypothesis testing section of this research paper would delve into the statistical methods used to assess the significance of the findings regarding multivariate stochastic dominance. It would likely detail the null and alternative hypotheses being tested (e.g., no dominance vs. dominance), the statistical test employed (potentially based on the Central Limit Theorem and bootstrap procedures developed earlier in the paper), and how the p-value or confidence intervals were calculated to determine the statistical significance of the results. A critical aspect would be the justification of the chosen test considering the assumptions made (e.g., sub-Gaussian distributions). Furthermore, the section might explore the power of the test, addressing its sensitivity in detecting true dominance relationships. Finally, it would discuss practical considerations, such as multiple hypothesis testing corrections (e.g., Bonferroni) to control for false positives when comparing numerous models. The overall goal of this section is to provide a statistically sound and rigorous method for assessing the claims about relative model performance.
Future Work#
The paper’s exploration of entropic multivariate stochastic dominance opens exciting avenues for future research. Extending the framework to other stochastic orders, like the μ-first order dominance or multivariate Lorenz order, is crucial for broader applications. This would involve establishing central limit theorems for the relevant optimal transport potentials. Investigating the impact of different cost functions on the resulting stochastic dominance tests is also important, particularly for domain-specific applications. This includes exploring the use of data-driven cost functions to create customized measures of dominance. Developing more robust multi-testing procedures which might incorporate additional dependence structures between metrics is another significant area. Current methods like Bonferroni correction can be conservative, potentially impacting power. Finally, applications to other large-scale ranking and benchmarking problems, beyond large language models, are a natural direction for future work. This could include evaluating the effectiveness of the methodology on different datasets and across various fields where multi-metric evaluation is critical.
More visual insights#
More on figures

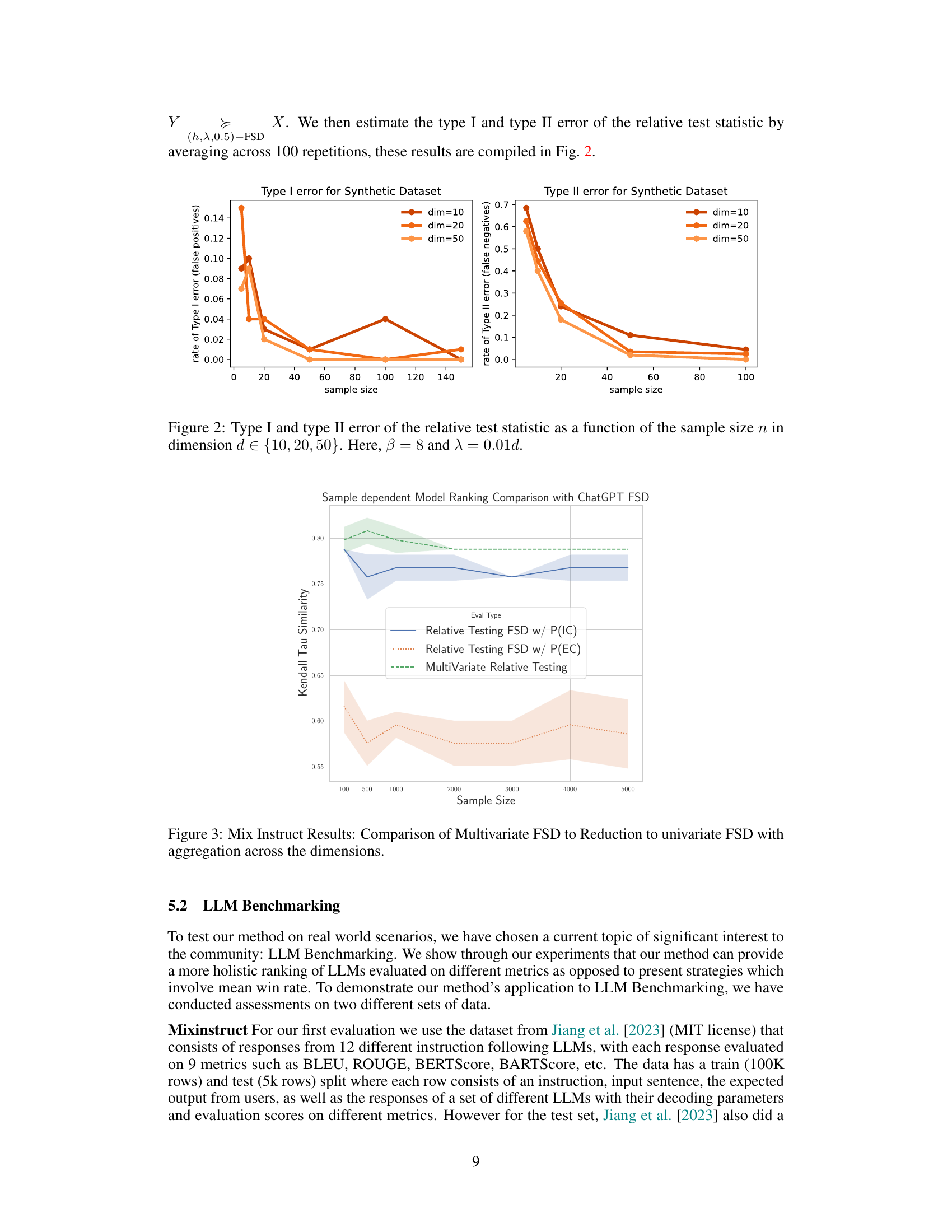
🔼 This figure shows the Type I and Type II error rates for a relative test statistic used in multivariate stochastic dominance testing. The error rates are plotted against the sample size (n) for different dimensions (d = 10, 20, and 50). The parameters β and λ are held constant at β=8 and λ=0.01d. The figure illustrates how the error rates behave as the sample size increases, for varying dimensions, providing insights into the test’s performance.
read the caption
Figure 2: Type I and type II error of the relative test statistic as a function of the sample size n in dimension d ∈ {10, 20, 50}. Here, β = 8 and λ = 0.01d.
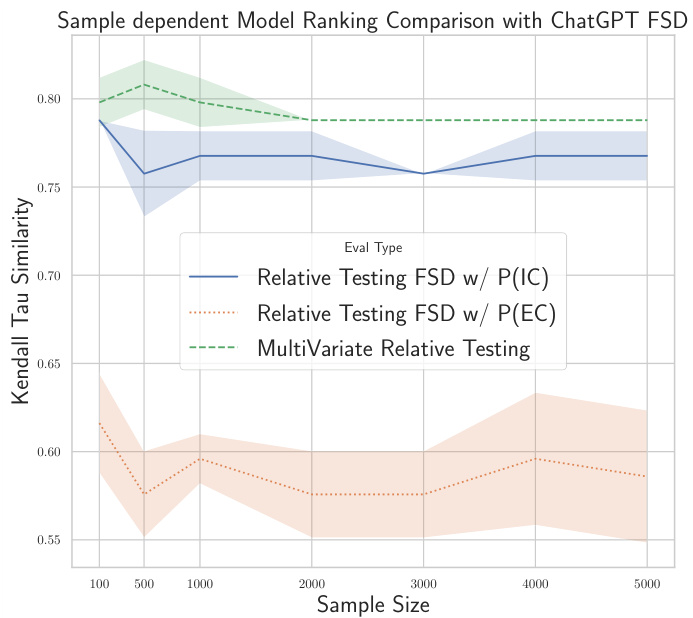
🔼 This figure compares the performance of three different methods for ranking large language models (LLMs) based on multiple evaluation metrics. The x-axis represents the sample size used in the experiment. The y-axis shows the Kendall Tau similarity between the rankings produced by each method and the rankings produced by ChatGPT, used as a human-proxy ranking. The three methods are: 1. Relative Testing FSD w/ P(IC): This method reduces the multivariate ranking problem to a univariate problem using independent copula aggregation across the dimensions before applying univariate first-order stochastic dominance. 2. Relative Testing FSD w/ P(EC): This method also reduces the problem to a univariate one using empirical copula aggregation before applying first-order stochastic dominance. 3. Multivariate Relative Testing: This method directly utilizes the multivariate first-order stochastic dominance framework, incorporating the dependencies between the metrics. The figure demonstrates that the multivariate relative testing approach outperforms the two univariate reduction methods in terms of Kendall Tau similarity with the human-generated rankings, especially with larger sample sizes. This indicates that accounting for dependencies between metrics through multivariate analysis yields a more accurate and robust ranking of LLMs.
read the caption
Figure 3. Mix Instruct Results: Comparison of Multivariate FSD to Reduction to univariate FSD with aggregation across the dimensions.
Full paper#