↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the critical issue of depth refinement in computer vision, enhancing accuracy, edge quality, and efficiency. It introduces a novel self-distillation framework to improve robustness, directly impacting applications like virtual reality, image generation, and 3D reconstruction. The method’s generalizability and strong performance across various benchmarks highlight its potential to advance current research, opening doors for developing more robust refinement models.
Visual Insights#

Figure 1(a) shows a visual comparison of different depth refinement approaches, highlighting the inconsistent billboard and wall (local inconsistency noise) and blurred depth edges (edge deformation noise) in existing methods. The figure demonstrates that the proposed method, SDDR, outperforms existing methods in terms of depth accuracy and edge quality. Figure 1(b) presents a quantitative comparison of these methods in terms of FLOPs (floating-point operations), showcasing SDDR’s efficiency advantage.
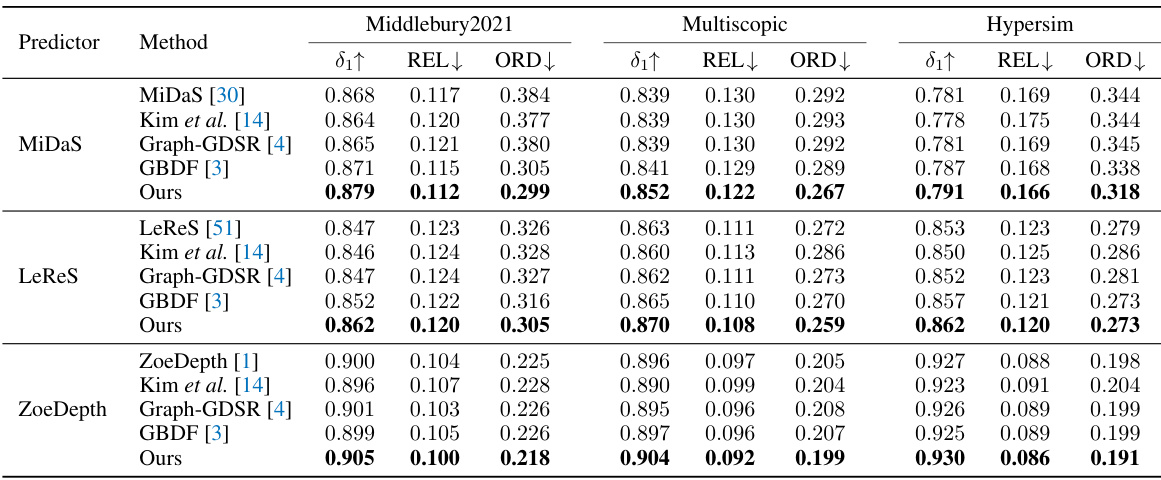
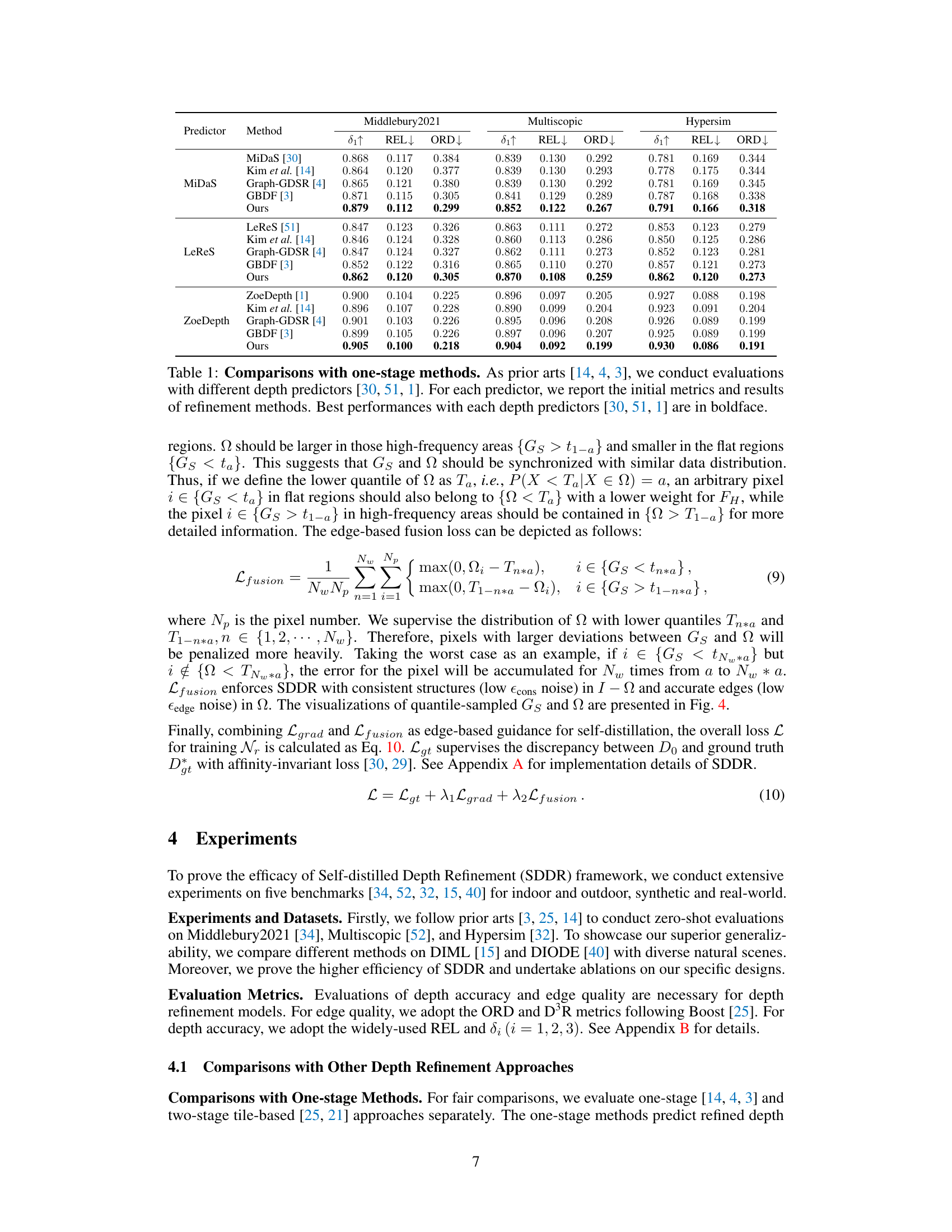
This table presents a comparison of the proposed Self-distilled Depth Refinement (SDDR) method against other state-of-the-art one-stage depth refinement methods. The comparison is performed using three different depth predictors (MiDaS, LeReS, and ZoeDepth) and evaluates the performance using the metrics δ1, REL, and ORD. The best results for each depth predictor are highlighted in bold, demonstrating the superior performance of SDDR across various baselines. The table showcases the effectiveness of SDDR in improving depth accuracy and edge quality.
In-depth insights#
Noisy Fusion Model#
A noisy fusion model, in the context of depth refinement, addresses the challenge of integrating low-resolution depth maps with high-resolution details while dealing with inherent noise and inconsistencies. It acknowledges that depth estimations are rarely perfect, containing inaccuracies and noise from various sources. The model explicitly incorporates noise as a fundamental part of the process, rather than trying to eliminate it. This is done by modeling the depth refinement problem as a noisy Poisson fusion process, which accounts for both local inconsistency noise (representing inconsistencies in depth structures, such as a disrupted billboard) and edge deformation noise (representing blurred or inaccurate depth boundaries). The noisy fusion model’s strength lies in its ability to robustly handle these types of noise, leading to improvements in depth accuracy, edge quality, and generalization performance. By explicitly acknowledging and modeling the noise, the model learns to effectively extract relevant information and mitigate the negative impact of inaccuracies during the refinement process. The model’s self-distillation approach, which uses low-noise edge representations as pseudo-labels for training, further improves its robustness and the quality of results.
Self-Distilled Refinement#
Self-distilled refinement represents a novel approach to enhance the accuracy and detail of depth maps, addressing limitations of existing methods. The core idea is to leverage self-distillation, where a model learns to refine its own predictions, creating improved pseudo-labels for training. This iterative process refines the model’s understanding of depth edges and inconsistencies, leading to significant improvements in accuracy and detail. The self-distillation framework offers a robust solution particularly effective in handling noisy data common in real-world depth estimation. By addressing issues like fuzzy boundaries and inconsistent depth structures, it is positioned to improve depth-based applications. The efficiency of this method over traditional patch-based techniques is also a significant advantage, making it a practical solution for high-resolution depth refinement tasks.
Edge-Based Guidance#
The heading ‘Edge-Based Guidance’ suggests a method to improve depth refinement by leveraging edge information. This likely involves a loss function that penalizes deviations from ground truth edges, encouraging the model to produce sharper, more accurate boundaries between depth discontinuities. The use of edge information is crucial because high-resolution depth maps often suffer from blurry or inaccurate edges. A likely implementation would involve calculating gradients of the predicted depth map and comparing them to ground truth edge maps. This approach might involve a combination of loss functions to balance the overall depth accuracy and the quality of the predicted edges. Self-distillation is another important concept that likely enhances edge quality. This technique trains the model using its own predicted edge maps as pseudo-labels, gradually refining these predictions through iterative training. The combination of these techniques might produce highly accurate, efficient depth refinement with superior edge detail compared to existing methods, which tend to suffer from inconsistencies and fuzzy boundaries.
Benchmark Results#
A dedicated ‘Benchmark Results’ section would ideally present a detailed comparison of the proposed method against existing state-of-the-art techniques. This would involve presenting quantitative metrics (e.g., accuracy, precision, recall, F1-score, etc.) across multiple relevant benchmarks. Visualizations, such as graphs and tables clearly showing performance differences, are crucial for effective communication. The choice of benchmarks is critical; they should represent a diverse range of scenarios and difficulty levels to demonstrate the generalizability and robustness of the proposed approach. Statistical significance testing should be applied to confirm that observed performance improvements are not merely due to chance. Furthermore, a discussion of the limitations of the benchmark datasets themselves, and how these limitations might influence the results, adds to the overall credibility and scientific rigor. Finally, qualitative analysis comparing the output of different methods on select examples would provide valuable insights into the strengths and weaknesses of each approach. Overall, a strong benchmark analysis offers compelling evidence supporting the claims and contributions of the research paper.
Future Works#
Future work could explore several promising avenues. Improving the robustness of SDDR to various challenging conditions such as low light, specular surfaces, or heavy occlusions is crucial for broader applicability. Investigating the use of different depth edge representation methods, potentially exploring techniques beyond gradient-based methods, could enhance performance. Expanding the application of the self-distillation framework to other computer vision tasks beyond depth refinement would be beneficial. Exploring alternative loss functions and optimization strategies could further refine the model’s accuracy and efficiency. Finally, developing a more comprehensive benchmark that includes a wider range of scenes and more challenging real-world conditions would allow for a more thorough evaluation of depth refinement methods and contribute to the advancement of this important research area.
More visual insights#
More on figures

This figure visually explains how depth prediction errors are modeled in the paper. It uses two examples of high-quality depth maps as a baseline (ideal depth D*). The figure then shows how the predicted depth (D) deviates from this ideal, breaking down the error into two components: local inconsistency noise (εcons) representing inconsistencies in depth structures and edge deformation noise (εedge) showing blurred or inaccurate depth edges. The figure illustrates how the combination of these two noise types approximates the overall depth error (D - D*).

This figure provides a visual overview of the Self-distilled Depth Refinement (SDDR) framework. It shows the process starting from the initial depth prediction and edge representation, through a coarse-to-fine refinement stage that generates accurate depth edges as pseudo-labels for self-distillation. The refinement network (Nr) uses these pseudo-labels along with edge-based guidance (edge-guided gradient loss and edge-based fusion loss) to produce the final refined depth map with consistent structures and fine-grained edges. The process incorporates a learnable soft mask (Ω) for high-frequency areas, balancing consistency and detail.

This figure visualizes the steps involved in the coarse-to-fine edge refinement process of the SDDR framework. It shows how the initial depth and edge predictions are iteratively refined across multiple steps (s=0, 1, 2, 3). Each step involves partitioning the image into windows, refining the depth within each window, and generating a refined depth map and edge representation for the entire image. The process culminates in a final refined depth map and edge representation (Gs) that are used as pseudo-labels for self-distillation.

This figure compares the performance of several one-stage depth refinement methods on real-world images. The input is a low-resolution depth map from the LeReS [51] model. The figure shows the original image and the resulting depth maps from the LeReS model, the Kim et al. model, the GBDF model, and the proposed SDDR model. SDDR shows significant improvements in terms of depth map quality, particularly around edges and fine details, indicating better performance.

This figure compares the performance of various two-stage depth refinement methods on natural scene images. The top row shows an image of shelves with items, and the bottom row displays an image of ice-covered branches. Each column represents a different method: ZoeDepth (baseline), PatchFusion, Boost, and the proposed method (Ours). The figure highlights that SDDR produces more accurate and consistent depth edges and structures compared to existing tile-based approaches.
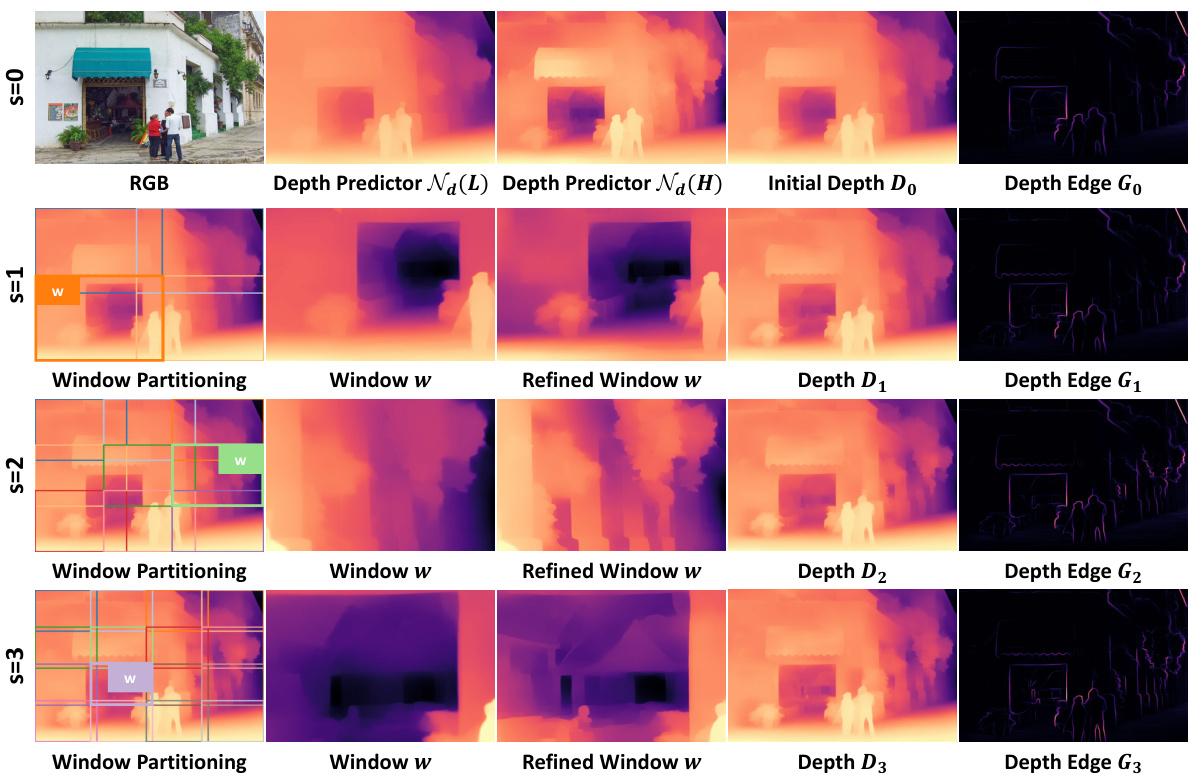
This figure visualizes the process of coarse-to-fine edge refinement in the SDDR framework. It shows how the low-resolution and high-resolution depth predictions are used to generate an initial refined depth map and edge representation. Then, through iterative refinement, the depth map and edge representation are further refined using window partitioning, which helps in achieving a balanced consistency and detail preservation. The final step shows the refined depth and edge representation (Gs), which serves as pseudo-labels for self-distillation.

The figure compares the depth estimation results of the proposed method and Boost [25] with different inference resolutions. The proposed method uses an adaptive resolution adjustment technique, resulting in fewer artifacts compared to Boost [25], especially in the areas with complex scene structures. This shows the effectiveness of the proposed adaptive resolution strategy in handling diverse scenes.

This figure shows how the edge-guided gradient loss (Lgrad) is calculated in the SDDR framework. It illustrates that Lgrad focuses mainly on high-frequency regions (Pn) identified through clustering, while preserving consistency in flat areas. The pseudo-label Gs, representing depth edge information, is used to supervise the learning process in the high-frequency regions. This targeted approach enhances the accuracy of depth edges in detail-rich areas without compromising the overall consistency of the depth map.

This figure visualizes the learnable region mask Ω and the pseudo-label Gs, before and after quantile sampling, to illustrate the edge-based fusion loss in the SDDR framework. Different colors represent different ranges of pixel values. The alignment of Ω and Gs ensures a balance between consistency and detail in the refined depth map, leveraging the one-stage refinement process and the learnable soft mask’s fine-grained feature fusion.
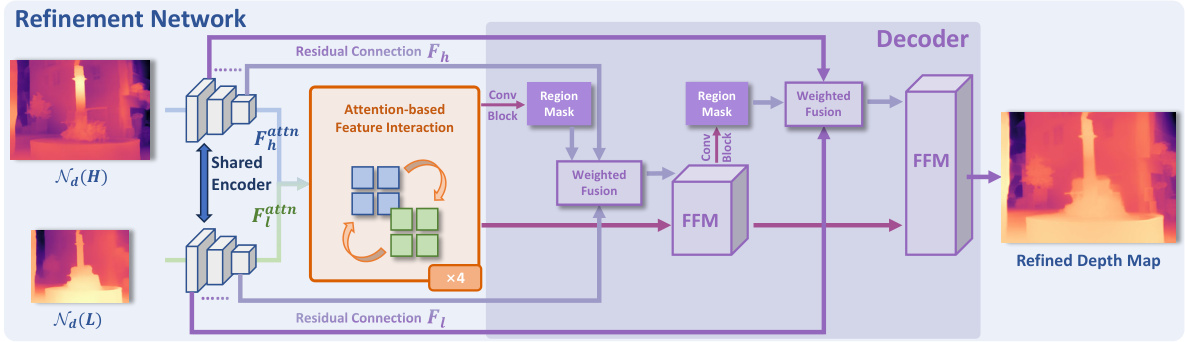
This figure shows the architecture of the refinement network used in the SDDR framework. It’s a U-Net-like architecture with a shared encoder that processes both low and high-resolution depth map predictions from the depth predictor. The encoder outputs are then fed into an attention-based feature interaction module to combine information from both resolutions. This combined information, along with regional masks (Ω), are passed through a series of convolution blocks and feature fusion modules (FFM) before the final refined depth map is produced. The decoder part of the network progressively upsamples the features to the final output resolution.

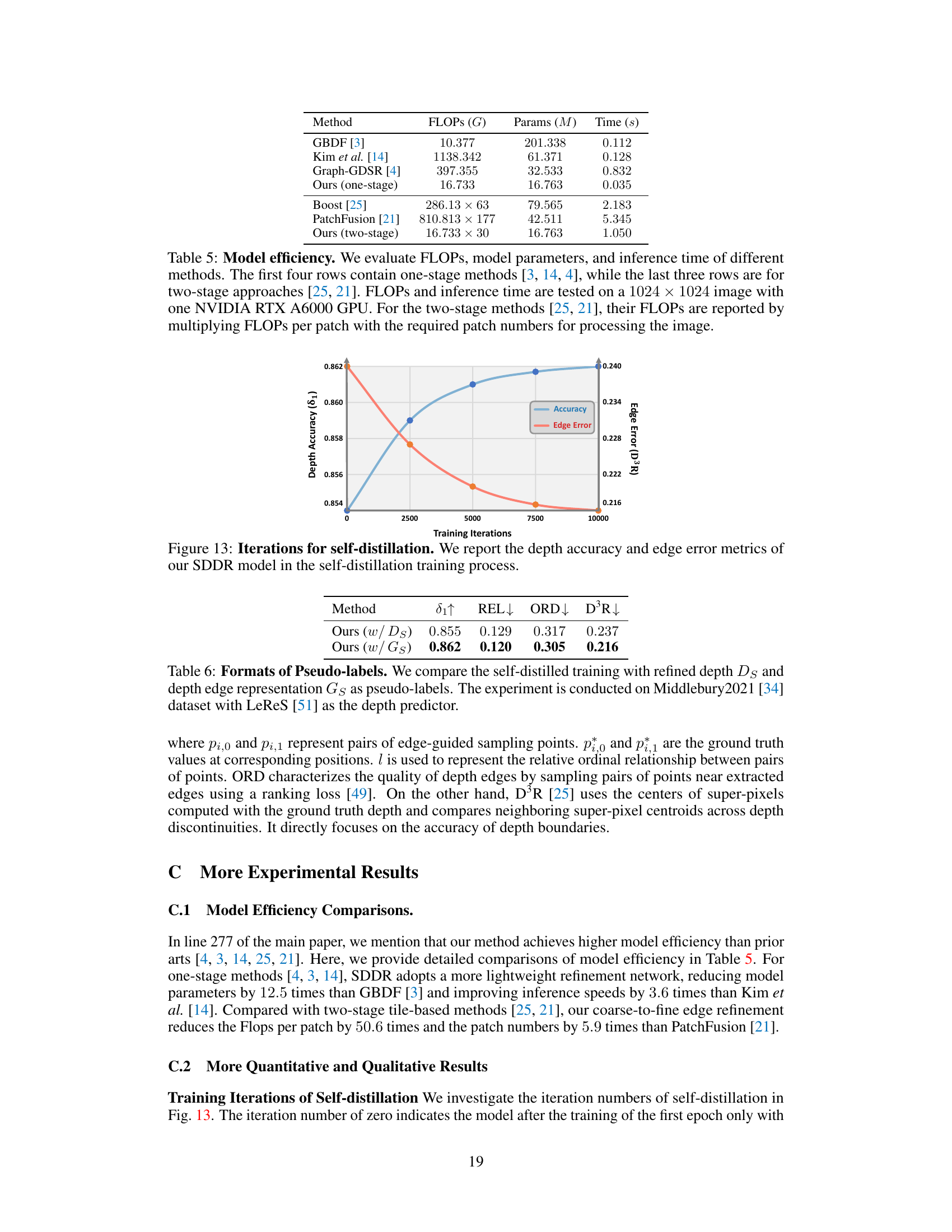
The figure shows the depth accuracy (δ1) and edge error (D³R) of the SDDR model during the self-distillation training process. The x-axis represents the number of training iterations, while the y-axis shows the depth accuracy and edge error. The plot demonstrates how the model’s accuracy improves and its edge error decreases as the number of training iterations increases, showcasing the effectiveness of the self-distillation process in refining depth predictions.
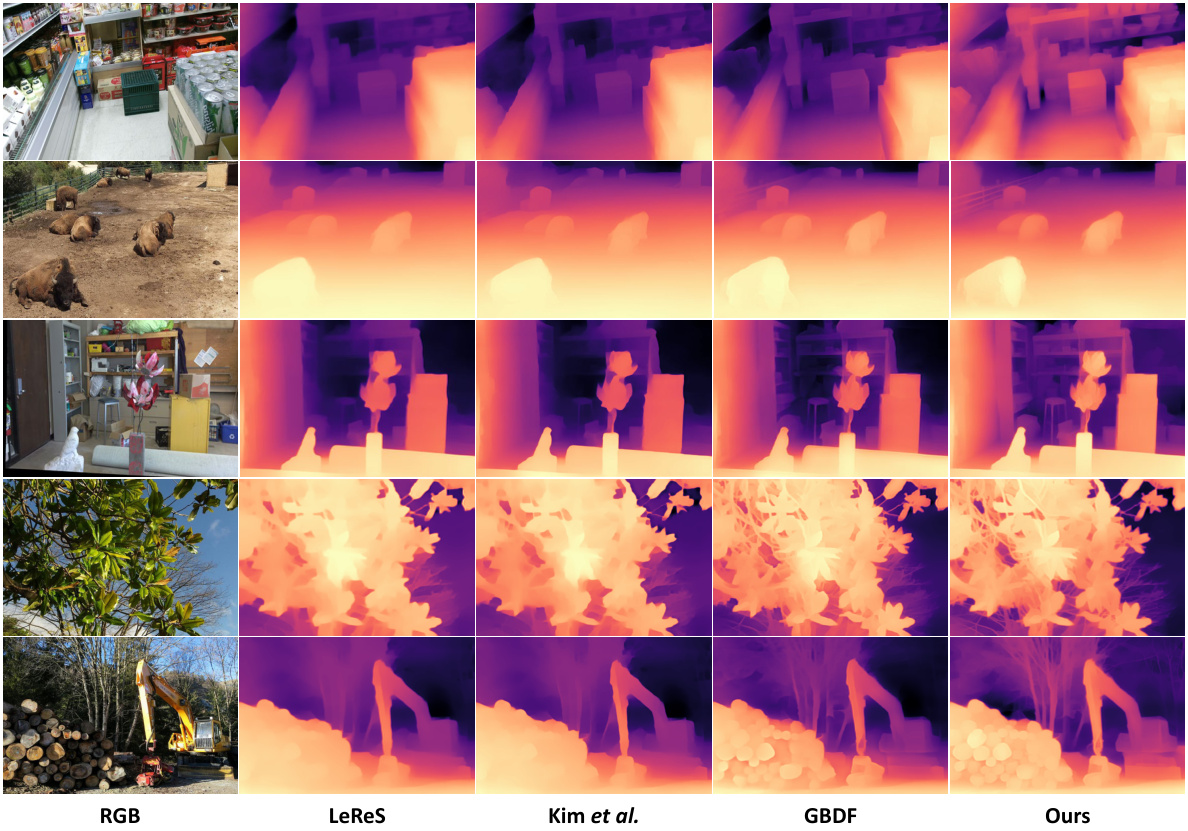
This figure compares the results of several depth refinement methods (LeReS, Kim et al., GBDF, and the proposed SDDR method) on natural scenes using LeReS as the depth predictor. The qualitative results show that SDDR outperforms the other methods in terms of edge sharpness and detail. SDDR is particularly effective in capturing fine details, such as intricate branches, that other methods struggle to capture.

This figure compares the performance of several two-stage depth refinement methods, including PatchFusion and Boost, against the proposed method (Ours) on various datasets. The image shows RGB input images, along with the depth maps generated by each method. The proposed method demonstrates improved accuracy and detail, particularly near edges and fine details, suggesting better consistency and overall performance than the existing methods.
More on tables
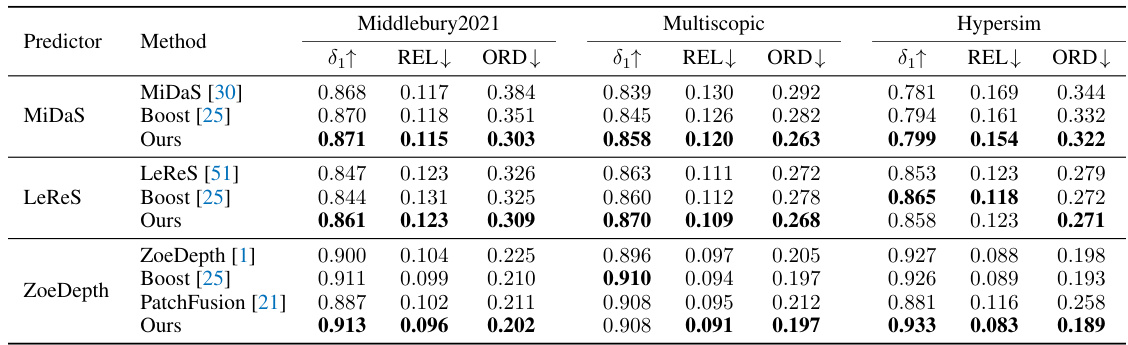
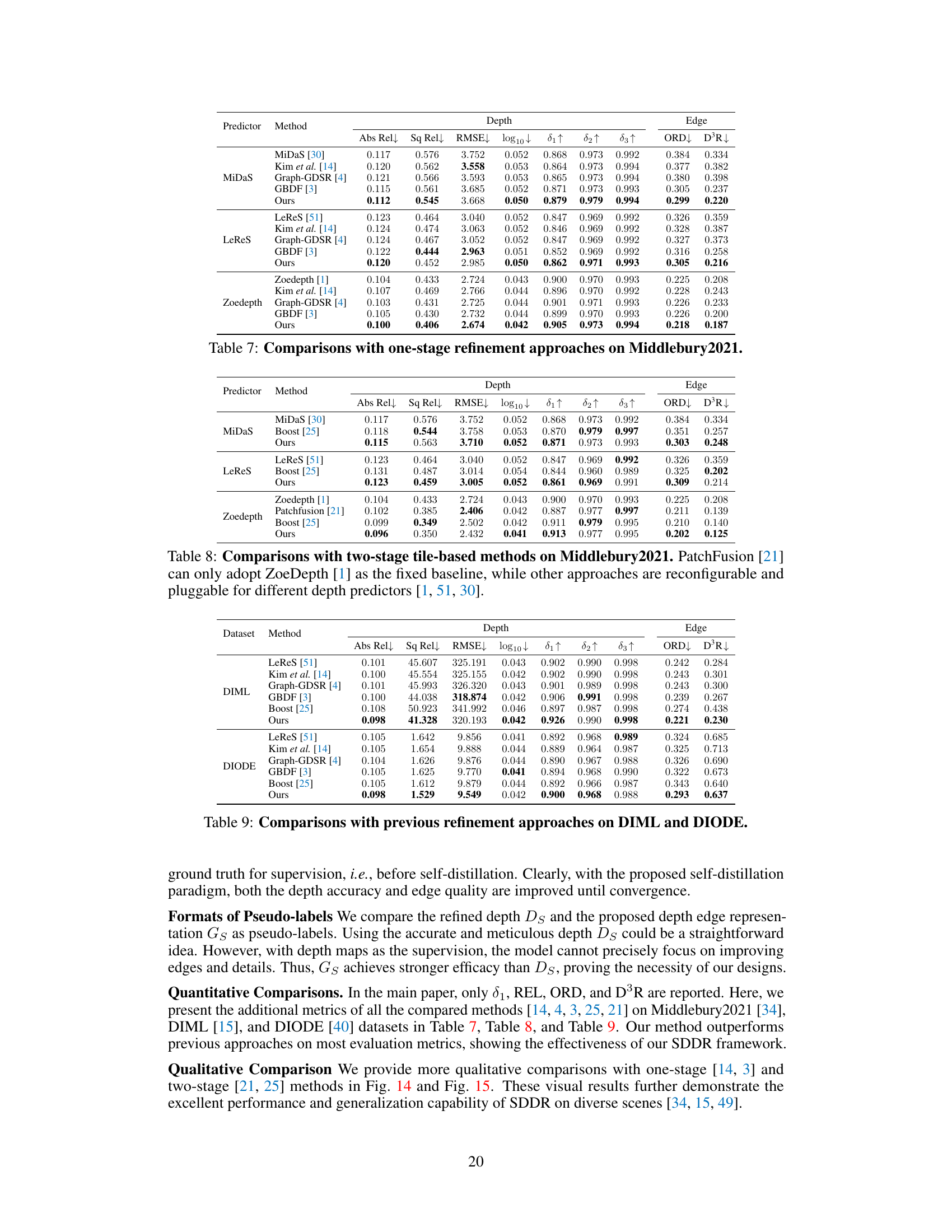
This table presents a comparison of the proposed Self-distilled Depth Refinement (SDDR) method with several state-of-the-art one-stage depth refinement methods. The comparison is done across three different depth prediction models (MiDaS [30], LeReS [51], and ZoeDepth [1]) using standard metrics for depth accuracy (δ1, REL) and edge quality (ORD). The boldfaced numbers highlight the best performance achieved by each depth predictor. This table demonstrates the effectiveness of SDDR compared to existing methods in terms of depth accuracy and edge quality for different depth estimation models.
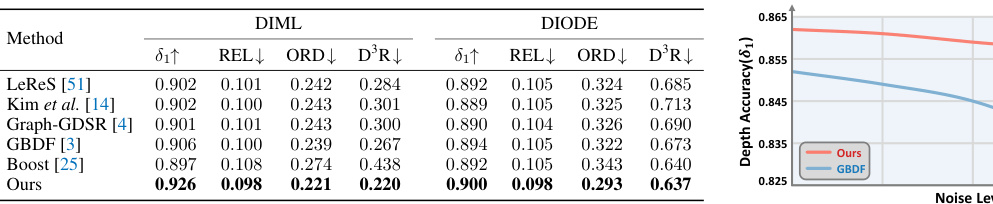
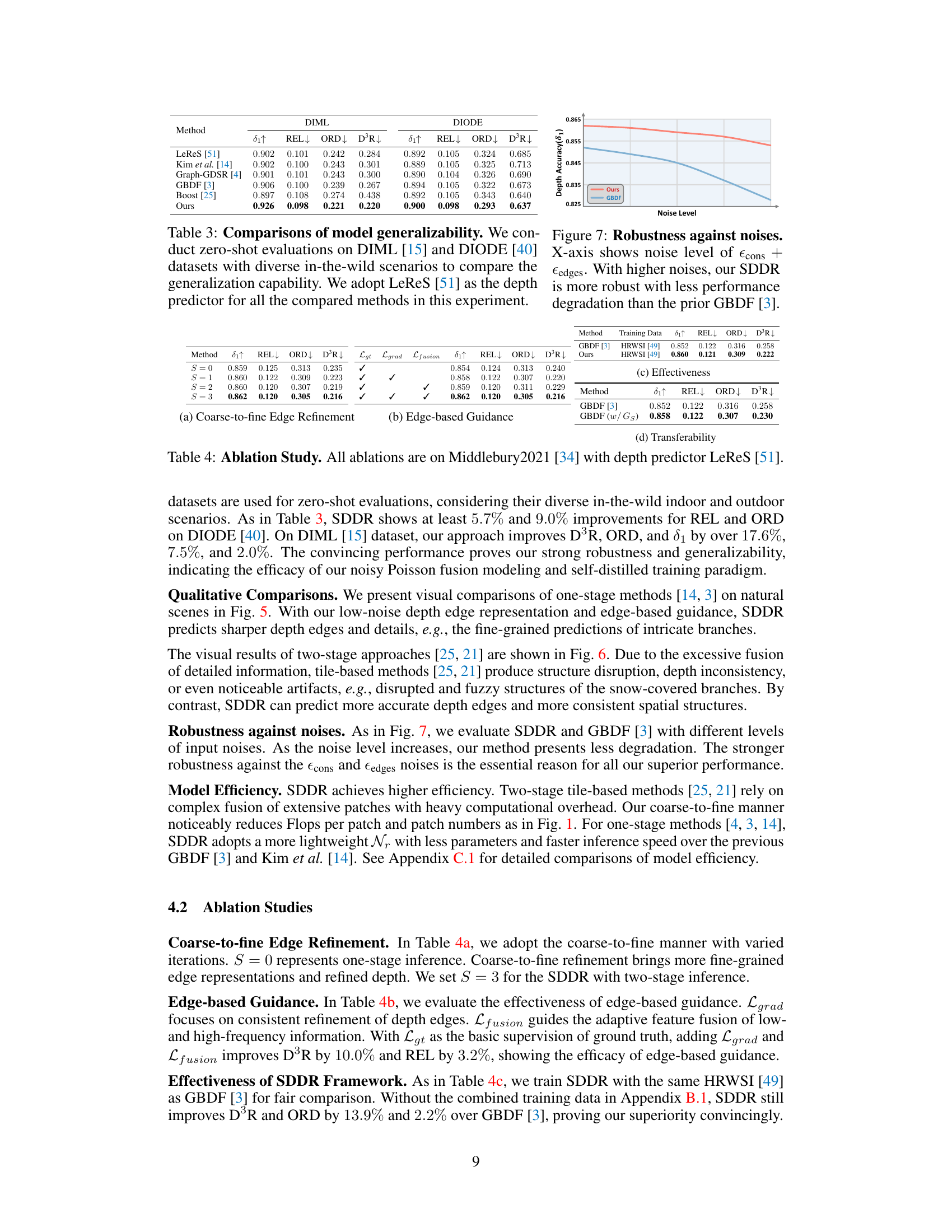
This table compares the generalization capabilities of different depth refinement methods on two real-world datasets: DIML and DIODE. The models were evaluated in a zero-shot setting, meaning they were not trained on these specific datasets. The metrics used to evaluate performance include: * δ1↑: Depth accuracy * REL↓: Relative error * ORD↓: Ordinal error * D³R↓: Depth discontinuity disagreement ratio Lower values for REL, ORD, and D³R indicate better performance. The results demonstrate the relative improvements in generalization ability achieved by the proposed SDDR method compared to existing state-of-the-art techniques.

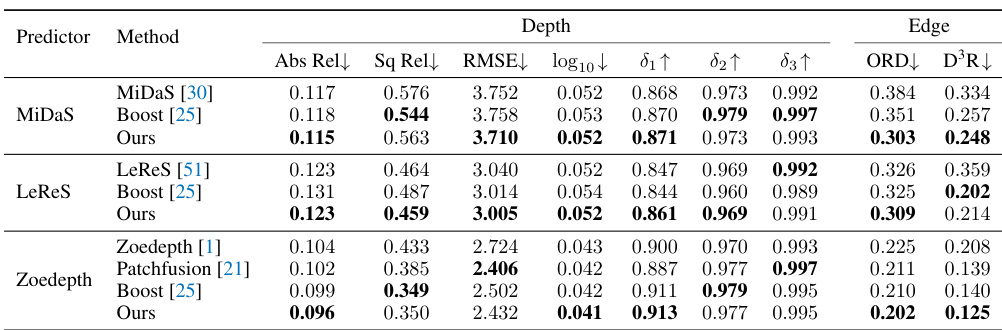
This table presents a comparison of the proposed Self-distilled Depth Refinement (SDDR) method with several existing one-stage depth refinement methods. The comparison is performed using three different depth predictors (MiDaS, LeReS, and ZoeDepth) on three datasets (Middlebury2021, Multiscopic, and Hypersim). The table shows the initial metrics (before refinement) for each depth predictor and the results after applying each refinement method. The best results for each depth predictor are highlighted in bold.

This table compares the model efficiency (FLOPs, parameters, and inference time) of different depth refinement methods. It categorizes methods into one-stage and two-stage approaches and shows that the proposed SDDR method is more efficient than others, especially the two-stage methods.

This table presents the ablation study results performed on the Middlebury2021 dataset using the LeReS depth predictor. It shows the impact of different components of the proposed Self-distilled Depth Refinement (SDDR) method by removing or modifying them and measuring the resulting changes in performance metrics (δ1↑, REL↓, ORD↓, D³R↓). Specifically, it investigates the effect of the coarse-to-fine edge refinement process (comparing different numbers of iterations), the edge-based guidance (removing or adding components of the loss function), and the training strategy (using the full training data or just a subset). The results demonstrate the contribution of each component to the overall performance improvement achieved by SDDR.
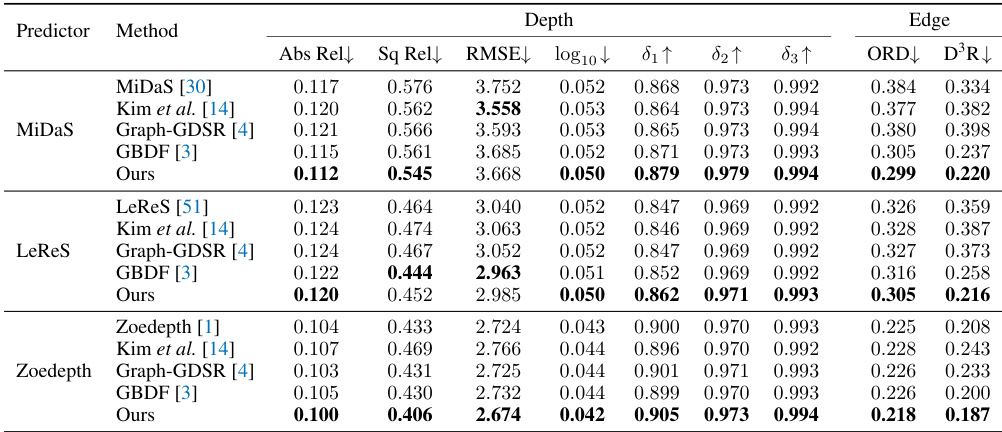
This table compares the performance of the proposed Self-distilled Depth Refinement (SDDR) method against other state-of-the-art one-stage depth refinement methods. The comparison is done using three different depth predictors (MiDaS [30], LeReS [51], and ZoeDepth [1]) to ensure fairness and generalizability. The table presents several metrics, including the initial depth estimation metrics (before refinement) and metrics after refinement by each method. The best performance for each predictor is highlighted in boldface.
This table compares the performance of SDDR against other one-stage depth refinement methods on three benchmark datasets (Middlebury2021, Multiscopic, and Hypersim) using three different depth predictors (MiDaS, LeReS, and ZoeDepth). The metrics used are δ1, REL, and ORD, showing SDDR’s superior accuracy and edge quality.

This table compares the performance of the proposed Self-distilled Depth Refinement (SDDR) method against other state-of-the-art one-stage depth refinement methods. The comparison is done using three different depth prediction models (MiDaS, LeReS, and ZoeDepth) as a baseline. The table shows metrics for depth accuracy (δ1, REL, ORD) for each method and model combination.
Full paper#