↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
System identification, crucial for control and robotics, is well-understood for linear systems but poses challenges for nonlinear counterparts. Existing methods often require complex ‘active exploration’ strategies, which can be resource-intensive and difficult to implement. A common approach is linearly parameterized nonlinear systems, which are more flexible than purely linear systems but also come with a need for efficient exploration techniques.
This research focuses on efficiently identifying this important class of systems. The authors show that if the nonlinear features of the system are ‘real-analytic’, which means they are infinitely differentiable, then simple, non-active exploration (i.e., using independent and identically distributed random input signals) is enough for accurate system identification. This is proved by developing non-asymptotic convergence rates for two common methods, least-squares and set-membership estimations. This discovery is supported by numerical simulations on pendulum and quadrotor examples, which showcase the efficient learning abilities of the methods under non-active exploration. This work significantly reduces the complexity of nonlinear system identification and opens doors for broader applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in control systems and machine learning because it bridges the gap between linear and nonlinear system identification. It offers novel theoretical guarantees for learning nonlinear systems using simple, non-active exploration, significantly advancing practical applications. The real-analyticity assumption highlights a key differentiator in system identification, opening avenues for exploring similar guarantees in other classes of nonlinear systems.
Visual Insights#

This figure compares the theoretical and empirical convergence rates of the least squares estimation (LSE) method for two different systems (pendulum and quadrotor) under different noise distributions (uniform and truncated Gaussian). The plots show that the empirical convergence rates closely match the theoretical rates, demonstrating the effectiveness of LSE in these scenarios.
In-depth insights#
Analytic Feature Impact#
The concept of ‘Analytic Feature Impact’ in a system identification context centers on how the smoothness and differentiability of feature functions influence the efficacy of non-active exploration methods. Real-analytic feature functions, unlike piecewise-affine functions, possess a key property: they cannot be identically zero on a set of positive measure unless they are identically zero everywhere. This characteristic is crucial because it ensures that even non-active exploration, using i.i.d. inputs, can still provide useful information for parameter estimation. The paper establishes that this property, combined with assumptions of bounded i.i.d. noises and a local input-to-state stability (LISS) condition, allows least-squares estimation (LSE) and set-membership estimation (SME) to efficiently learn the system parameters, providing non-asymptotic convergence rates. The real-analyticity assumption, therefore, highlights a fundamental distinction between the identifiability of smooth and non-smooth nonlinear systems when using passive exploration strategies, addressing a significant gap in the literature.
LSE/SME Convergence#
The paper analyzes the convergence properties of two system identification methods: Least Squares Estimation (LSE) and Set Membership Estimation (SME), focusing on linearly parameterized nonlinear systems. LSE’s convergence is proven to be efficient under specific conditions, primarily real-analytic feature functions and independent and identically distributed (i.i.d.) random inputs. This contrasts with existing literature which highlights the limitations of non-active exploration in general nonlinear system identification. The analysis establishes non-asymptotic convergence rates for both LSE and SME, showcasing the impact of real analyticity. The convergence rate is empirically tested with experiments on pendulum and quadrotor dynamics, validating the theoretical bounds. The results highlight the importance of differentiability in achieving successful system identification through non-active exploration, suggesting that non-smooth feature functions pose a significant challenge that might necessitate alternative, active exploration methods.
BMSB Condition Role#
The Block-Martingale Small-Ball (BMSB) condition plays a pivotal role in establishing non-asymptotic convergence rates for system identification, particularly within the context of linearly parameterized nonlinear systems. The core idea is to ensure that the feature functions, which are used to represent the system’s dynamics, exhibit sufficient richness and persistence of excitation, even under non-active exploration. In simpler terms, the BMSB condition guarantees that, with high probability, the system’s dynamics are sufficiently explored over time, preventing the algorithm from getting stuck in regions of limited information. This is especially crucial for nonlinear systems where simple i.i.d. inputs might not guarantee adequate exploration. The real-analyticity assumption on the feature functions is a crucial element for the success of non-active exploration, which relies on the property that an analytic function cannot be identically zero on a set of positive measure unless it is identically zero everywhere. This work shows that by satisfying the BMSB condition, even with i.i.d. inputs, convergence can be guaranteed. Therefore, the BMSB condition bridges the gap between the desirable properties of linear systems (achieving optimal convergence rates even with passive exploration) and the challenges posed by nonlinear systems, offering a powerful tool for theoretical analysis and performance guarantees.
Non-asymptotic Bounds#
The concept of “Non-asymptotic Bounds” in the context of a research paper signifies a significant departure from traditional asymptotic analysis. Instead of focusing on the limiting behavior of a system as the number of data points or time tends to infinity, non-asymptotic bounds provide finite-sample guarantees. This means that the results offer performance guarantees for a specific, finite amount of data, which is crucial for practical applications where data is always limited. The analysis typically involves probabilistic inequalities and concentration-of-measure techniques to bound the error or deviation within a specific probability, providing a more realistic and practical assessment of the system’s behavior. Crucially, non-asymptotic bounds are useful for determining appropriate sample sizes and assessing the reliability of model estimates. They provide a stronger form of analysis compared to traditional asymptotic analysis, which often doesn’t offer concrete guarantees for practical datasets.
Future Research#
The paper’s ‘Future Research’ section could explore several promising avenues. Relaxing the semi-continuity assumption for noise and input distributions would broaden applicability to systems with discrete disturbances. Deriving explicit formulas for the BMSB constants (sφ, pφ) would enhance the practicality of the theoretical bounds, possibly by investigating subclasses of systems. Extending the analysis to systems with imperfect state observations is crucial for real-world applicability. Investigating the volume of uncertainty sets estimated by SME rather than just diameter could provide a more comprehensive uncertainty quantification. Finally, exploring the impact of dependent data and more complex control policies on convergence would greatly enrich the theoretical understanding of nonlinear system identification.
More visual insights#
More on figures

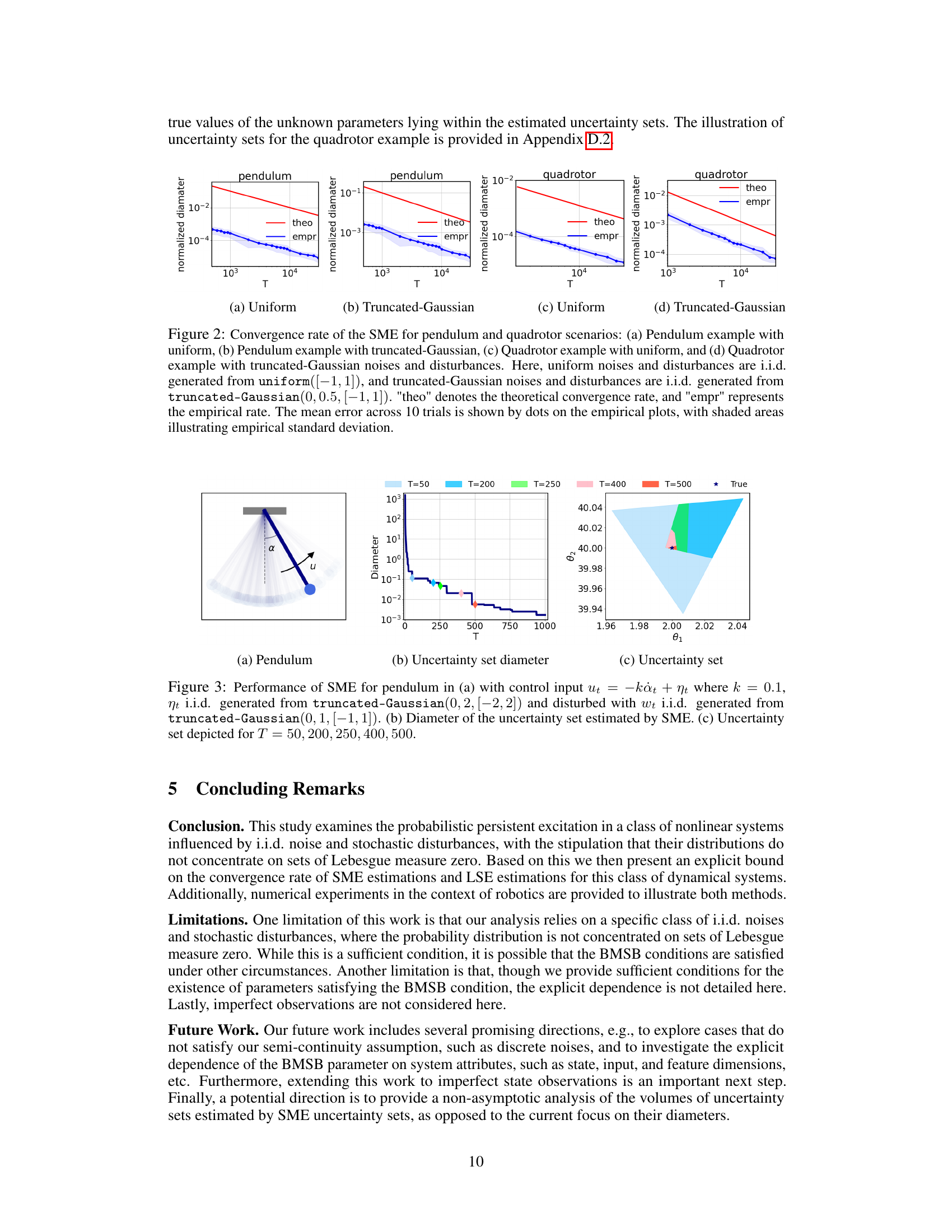
This figure compares the theoretical and empirical convergence rates of the Set Membership Estimation (SME) method for estimating the uncertainty set of parameters in a pendulum and quadrotor system. The plots show that the empirical convergence rates closely match the theoretical rates derived in the paper, for both uniform and truncated Gaussian noise distributions. The results support the claim that SME converges efficiently under independent and identically distributed (i.i.d) random inputs.

This figure shows the performance of Set Membership Estimation (SME) for a pendulum system. Panel (a) illustrates the pendulum system. Panel (b) presents a plot of the uncertainty set diameter versus trajectory length T. Panel (c) displays the uncertainty sets estimated by SME at different trajectory lengths, illustrating how they contract as the trajectory length increases. The true parameter values are shown for comparison.

This figure shows the 2D projections of the uncertainty sets estimated by the Set Membership Estimation (SME) method for the quadrotor example. Each plot displays two parameters’ uncertainty sets across different trajectory lengths (T = 200, 500, 1000, 2000) along with the ground truth (marked with a red star). The noises and disturbances are independently and identically distributed (i.i.d.) and generated from a truncated Gaussian distribution with mean 0, variance 0.5, and truncated range [-1, 1]. The figure illustrates how the uncertainty sets contract towards the true parameter values as the trajectory length increases.
Full paper#