TL;DR#
Matrix denoising, crucial in many fields, faces challenges with correlated noise. Existing methods either fail to precisely quantify the asymptotic error or yield suboptimal results, particularly when noise has both row and column correlations (doubly heteroscedastic). This limitation hinders achieving optimal performance in various applications.
This work overcomes this limitation by characterizing the exact asymptotic minimum mean square error (MMSE) for matrix denoising under doubly heteroscedastic noise. A novel spectral estimator is designed and rigorously proven optimal under a technical condition, attaining the minimum error when information-theoretically possible. The method uses tools from statistical physics and approximate message passing, differing significantly from standard random matrix theory approaches, and showcases superior performance compared to current state-of-the-art methods in numerical experiments.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a critical gap in matrix denoising, a fundamental problem across many scientific fields. By establishing the information-theoretic limits and designing an optimal spectral estimator for doubly heteroscedastic noise, the research provides principled solutions beyond existing suboptimal methods. This opens avenues for improved algorithms and a deeper understanding of fundamental limitations in high-dimensional data analysis. The connection made with statistical physics and message passing offer new avenues for theoretical analysis and algorithm development.
Visual Insights#
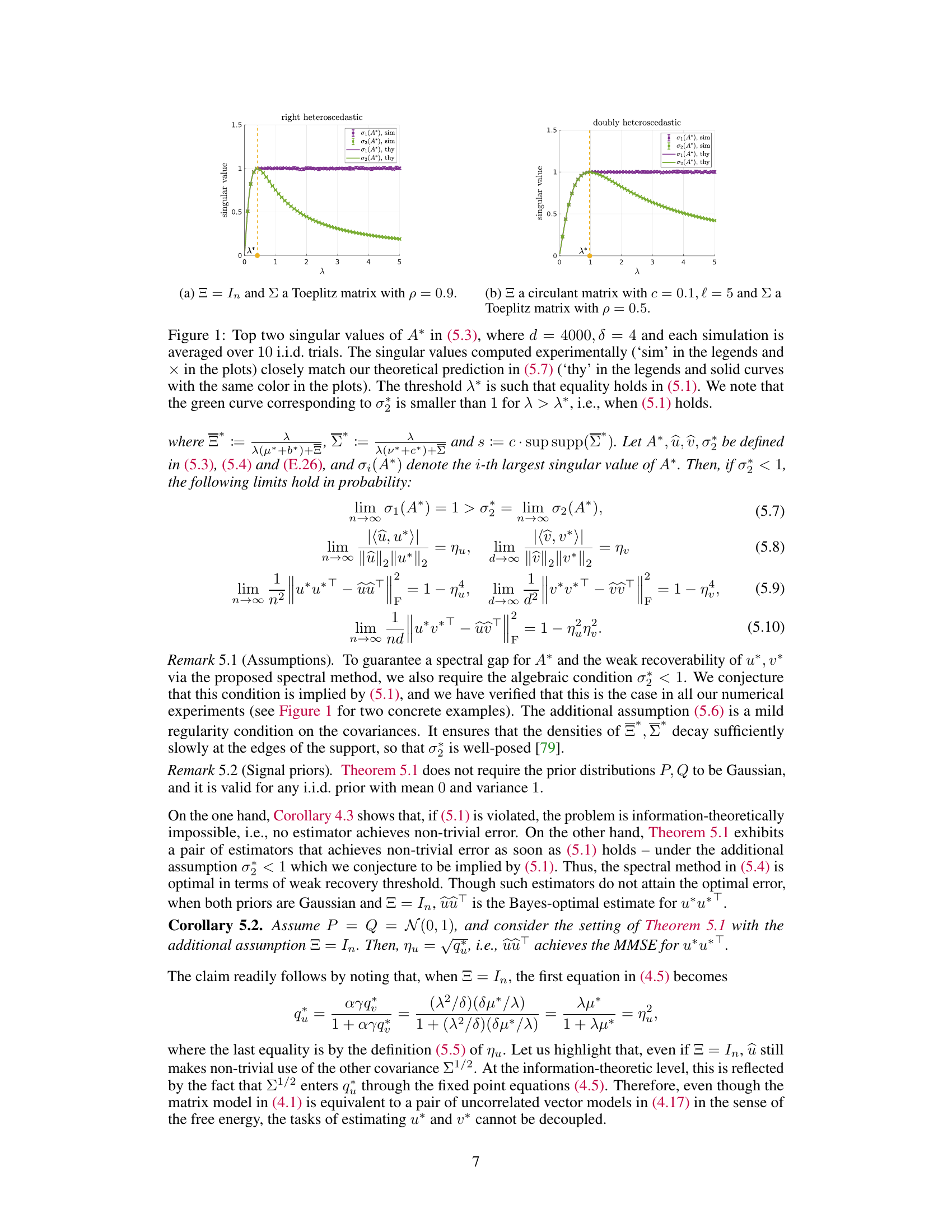
🔼 The figure shows the top two singular values of the pre-processed data matrix A*, obtained through the proposed spectral method. It compares simulated results (sim) with theoretical predictions (thy) for both one-sided and doubly heteroscedastic noise. The plot highlights the spectral gap that emerges above the threshold λ*, illustrating the efficacy of the method and validating theoretical analysis.
read the caption
Figure 1: Top two singular values of A* in (5.3), where d = 4000, δ = 4 and each simulation is averaged over 10 i.i.d. trials. The singular values computed experimentally ('sim' in the legends and × in the plots) closely match our theoretical prediction in (5.7) ('thy' in the legends and solid curves with the same color in the plots). The threshold λ* is such that equality holds in (5.1). We note that the green curve corresponding to σ½ is smaller than 1 for λ > λ*, i.e., when (5.1) holds.
In-depth insights#
Optimal Spectral Estimator#
The heading ‘Optimal Spectral Estimator’ suggests a significant contribution to signal processing or matrix recovery. The research likely involves developing a novel method to estimate a signal’s spectral components, which are crucial for extracting information from noisy or incomplete data. Optimality implies the method achieves the best possible performance under certain criteria, such as minimizing the mean squared error. This optimality is likely established through rigorous mathematical analysis, possibly using techniques from information theory or random matrix theory. The term ‘spectral’ indicates the method works directly in the frequency domain, offering potential computational advantages for high-dimensional data. The core of the estimator likely involves advanced linear algebra techniques, possibly utilizing singular value decomposition or eigen-decomposition to extract relevant information from the observed data. The results would likely demonstrate superior performance compared to existing approaches in various noise conditions and data regimes, ultimately offering a robust and efficient solution for the estimation of signals from noisy data.
Doubly Heteroscedastic Noise#
The concept of “doubly heteroscedastic noise” signifies a complex noise model in matrix denoising where noise possesses both row-wise and column-wise correlations, unlike simpler models. This complexity makes accurate estimation of the underlying signal challenging. Existing methods often fail to account for this double correlation structure, resulting in suboptimal performance. The paper tackles this challenge by proposing a novel spectral estimator with rigorous optimality guarantees. The estimator’s design is theoretically principled and leverages advanced techniques from statistical physics and approximate message passing. Numerical experiments demonstrate significant performance improvement over existing state-of-the-art methods, especially in low signal-to-noise ratio (SNR) scenarios. The authors’ approach highlights the importance of understanding the intricate noise structure for optimal matrix denoising and offers a powerful framework for handling more realistic noise models in various applications.
AMP-Based Analysis#
An AMP-based analysis of a matrix denoising problem would leverage the framework of Approximate Message Passing (AMP) to analyze the algorithm’s performance and derive theoretical guarantees. It would likely involve deriving state evolution equations to track the algorithm’s behavior in the high-dimensional limit, characterizing the algorithm’s asymptotic mean squared error (MSE), and potentially establishing conditions for optimality or phase transitions. A key aspect would be how the AMP equations incorporate the noise structure, especially if it’s doubly heteroscedastic, meaning it exhibits correlations in both rows and columns. The analysis might involve techniques from statistical physics, exploiting analogies between the algorithm’s dynamics and spin glass models or similar systems. The theoretical results obtained from the AMP analysis would likely inform the design of efficient spectral estimators, establishing connections between the algorithm’s fixed points and the optimal singular vectors of a pre-processed data matrix. Finally, it’s important to note that the rigorous analysis of AMP algorithms often requires technical assumptions on the noise distribution, signal priors and dimension scaling, and it is crucial to carefully state and discuss these conditions within the AMP-based analysis.
Information Limits#
The section on ‘Information Limits’ would ideally delve into the fundamental bounds on the accuracy achievable when estimating a rank-1 matrix from noisy observations. This involves characterizing the minimum mean squared error (MMSE), representing the best possible estimation accuracy under the given noise model and signal priors. A key aspect would be establishing the weak recovery threshold: the minimum signal-to-noise ratio (SNR) beyond which non-trivial estimation is information-theoretically possible. This threshold signifies a phase transition, separating regimes where accurate estimation is feasible from those where it is not. The analysis likely would leverage tools from statistical physics and random matrix theory to rigorously determine the MMSE and associated thresholds, potentially employing advanced techniques like the interpolation method or replica symmetry breaking to handle the complexities of correlated noise and high-dimensional settings. A central goal would be to prove the optimality (or sub-optimality) of existing estimation methods, demonstrating whether or not they achieve the fundamental information-theoretic limits under various conditions.
Future Research#
Future research directions stemming from this work could explore extending the theoretical framework to handle higher-rank matrices, moving beyond the rank-1 case considered in the paper. This would involve developing more sophisticated mathematical tools to analyze the complex interactions of multiple signals embedded in doubly heteroscedastic noise. Another key area is investigating the impact of different noise distributions beyond the Gaussian assumption, as real-world noise rarely follows this ideal model. Robustness analysis and algorithm design for non-Gaussian scenarios are crucial. Furthermore, the assumption of known covariance matrices is a simplification. A significant advancement would involve developing methods to estimate the noise covariance matrices directly from the observed data, which is a challenging problem in high dimensions. Finally, applying the proposed methodology to real-world datasets in diverse fields like genomics, image processing, or finance would validate the theoretical findings and reveal practical implications and limitations of this approach.
More visual insights#
More on figures

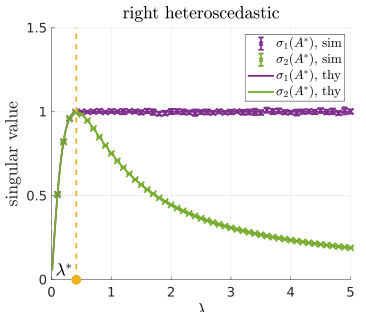
🔼 The figure shows the top two singular values of the preprocessed matrix A* plotted against the signal-to-noise ratio (SNR) λ. It compares simulated results (sim) with theoretical predictions (thy) for both one-sided and doubly heteroscedastic noise. The plot demonstrates a close match between simulation and theory, highlighting a spectral gap that emerges above a certain threshold (λ*). This threshold corresponds to the weak recovery threshold, indicating that the proposed algorithm is able to successfully recover the signals when the SNR is above this threshold.
read the caption
Figure 1: Top two singular values of A* in (5.3), where d = 4000, δ = 4 and each simulation is averaged over 10 i.i.d. trials. The singular values computed experimentally ('sim' in the legends and × in the plots) closely match our theoretical prediction in (5.7) ('thy' in the legends and solid curves with the same color in the plots). The threshold λ* is such that equality holds in (5.1). We note that the green curve corresponding to σ½ is smaller than 1 for λ > λ*, i.e., when (5.1) holds.
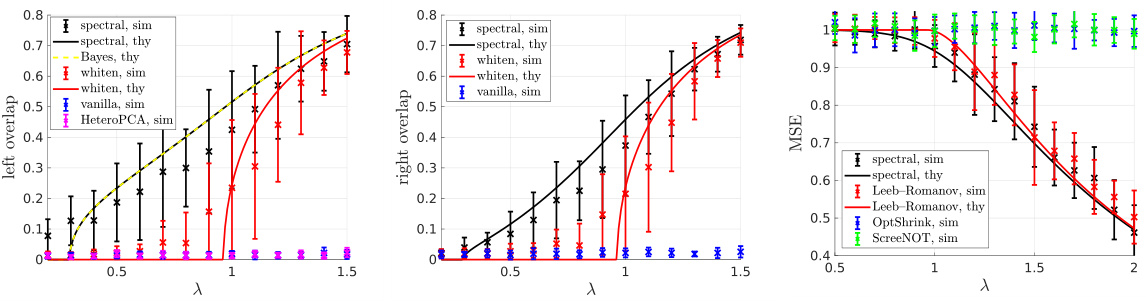
🔼 This figure compares the performance of different matrix denoising methods in the case of one-sided heteroscedasticity. The proposed spectral estimator significantly outperforms other methods, especially at low signal-to-noise ratios (SNR). The results are consistent with the theoretical predictions of Theorem 5.1. The plots show the normalized correlation with u* and v*, and the mean squared error (MSE) for uvT as a function of λ (SNR).
read the caption
Figure 2: Performance comparison when Ξ = In and ∑ is a circulant matrix. The numerical results closely follow the predictions of Theorem 5.1, and our spectral estimators in (5.4) outperform all other methods (Leeb–Romanov, OptShrink, ScreeNOT, and HeteroPCA), especially at low SNR.
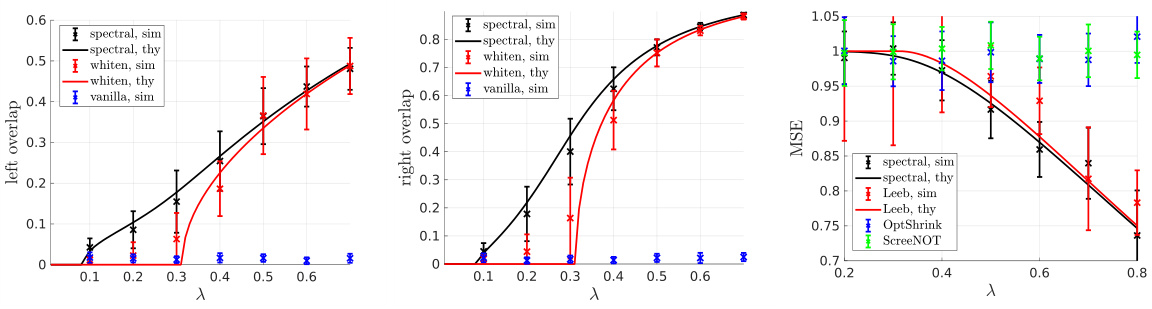
🔼 This figure compares the performance of the proposed spectral estimator with other existing methods for the one-sided heteroscedastic case, where the noise covariance matrix Ξ is the identity matrix and the covariance matrix Σ is a circulant matrix. The plots show normalized correlation with u* and v*, and the mean squared error (MSE) for uvT, all as functions of λ (the signal-to-noise ratio). The results demonstrate that the proposed spectral estimator achieves higher correlation with the true signals and lower MSE, particularly at low SNR, compared to other methods like Leeb–Romanov, OptShrink, ScreeNOT, and HeteroPCA.
read the caption
Figure 2: Performance comparison when Ξ = In and ∑ is a circulant matrix. The numerical results closely follow the predictions of Theorem 5.1, and our spectral estimators in (5.4) outperform all other methods (Leeb–Romanov, OptShrink, ScreeNOT, and HeteroPCA), especially at low SNR.
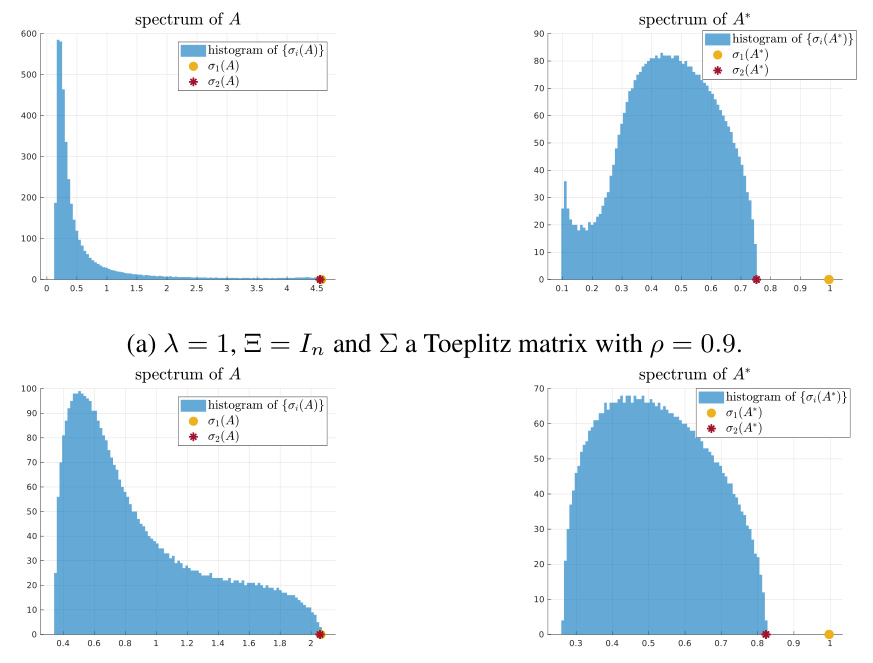
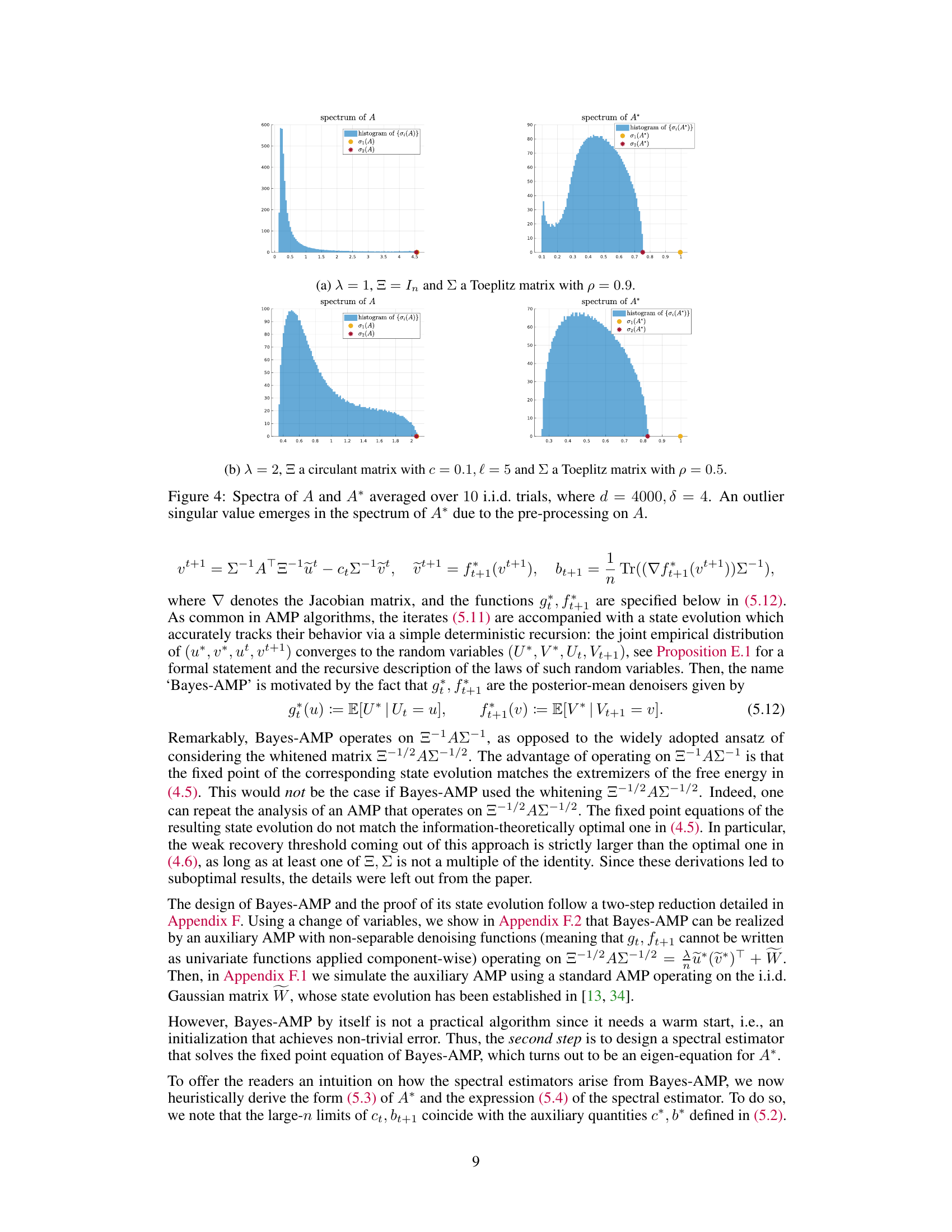
🔼 The figure shows the top two singular values of matrix A*, computed experimentally and theoretically, for both one-sided and doubly heteroscedastic noise. It demonstrates the close match between the experimental and theoretical results and highlights the threshold λ* beyond which condition (5.1) is satisfied, indicating the possibility of non-trivial estimation error.
read the caption
Figure 1: Top two singular values of A* in (5.3), where d = 4000, δ = 4 and each simulation is averaged over 10 i.i.d. trials. The singular values computed experimentally ('sim' in the legends and × in the plots) closely match our theoretical prediction in (5.7) ('thy' in the legends and solid curves with the same color in the plots). The threshold λ* is such that equality holds in (5.1). We note that the green curve corresponding to σ½ is smaller than 1 for λ > λ*, i.e., when (5.1) holds.
Full paper#