Single-Loop Stochastic Algorithms for Difference of Max-Structured Weakly Convex Functions

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on non-convex, non-smooth optimization problems, particularly those involving differences of max-structured weakly convex functions and weakly convex-strongly concave min-max problems. It offers a novel single-loop stochastic algorithm, improving efficiency over existing double-loop methods, and opens avenues for developing more efficient solutions to similar challenging optimization tasks.

Visual Insights

#

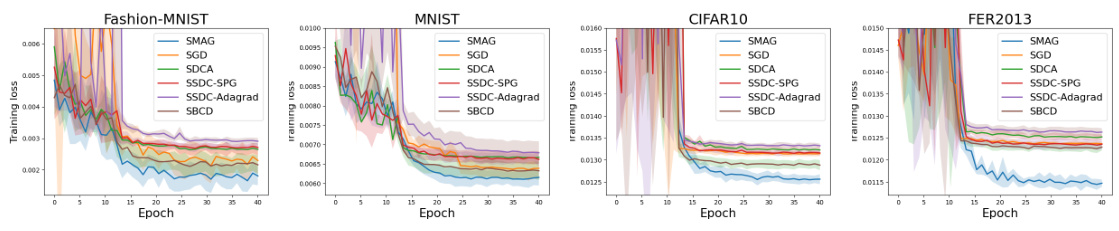
🔼 This figure compares the training loss curves of different algorithms for Positive-Unlabeled (PU) learning on four datasets: Fashion-MNIST, MNIST, CIFAR10, and FER2013. The algorithms compared include SMAG (the authors’ proposed algorithm), SGD, SDCA, SSDC-SPG, SSDC-Adagrad, and SBCD. The x-axis represents the training epoch, and the y-axis represents the training loss. The shaded regions represent the standard deviation across multiple runs for each method. The figure shows SMAG achieving lower training loss than the baseline methods across all datasets.

read the caption

Figure 1: Training Curves of PU Learning

🔼 This table compares the proposed single-loop stochastic algorithm SMAG with existing double-loop stochastic methods for solving difference-of-weakly-convex (DWC) problems. It contrasts the smoothness assumptions made about the objective functions (smooth, Hölder continuous gradient, non-smooth), the resulting complexity in terms of epsilon (ε), and the number of loops required in the algorithm. The asterisk (*) indicates that the SBCD method was originally designed for a specific problem but can be generalized.

read the caption

Table 1: Comparison with existing stochastic methods for solving DWC problems with non-asymptotic convergence guarantee. * The method SBCD is designed to solve a problem in the form of minx{miny $(x, y) – minz f(x, z)} with a specific formulation of 4 and 4. However, the method and analysis can be generalized to solving non-smooth DWC problems.

In-depth insights

#

DMax Optimization

#

The concept of “DMax Optimization” presented in the research paper appears to be a novel framework unifying two important problem classes in machine learning: Difference of Weakly Convex functions (DWC) and Weakly Convex Strongly Concave min-max problems (WCSC). This unification is significant because it allows the development of a single, general algorithm to solve a wider range of problems that previously required separate approaches. The core idea seems to involve using the Moreau envelope to create smooth approximations of the non-smooth, non-convex objectives, enabling the application of efficient gradient-based methods. The resulting algorithm, dubbed SMAG, is a particularly exciting development since it operates in a single-loop manner, offering improved efficiency compared to existing double-loop algorithms. This suggests a potential for considerable improvements in computational speed and scalability, making it more practical for large-scale datasets. The paper’s contribution extends beyond the development of SMAG to also include a rigorous convergence analysis, establishing state-of-the-art theoretical guarantees. The practical impact is demonstrated through experimental results on tasks such as positive-unlabeled learning and partial AUC optimization with fairness regularizers, showcasing the versatility and effectiveness of the DMax optimization approach.

SMAG Algorithm

#

The SMAG algorithm, a single-loop stochastic method, offers a novel approach to solving the Difference of Max-Structured Weakly Convex Functions (DMax) optimization problem. Its key innovation lies in efficiently approximating gradients of Moreau envelopes, avoiding the computationally expensive nested loops found in existing methods. By using only one step of stochastic gradient updates for both primal and dual variables, SMAG achieves a state-of-the-art convergence rate of O(ε⁻⁴). This makes it particularly attractive for large-scale applications where efficiency is paramount. The algorithm’s effectiveness is demonstrated through empirical results on positive-unlabeled learning and partial AUC optimization, showcasing its versatility and potential for broader application in machine learning and related fields. The algorithm’s single-loop structure simplifies implementation and reduces hyperparameter tuning, making it a more practical solution for real-world problems. However, its reliance on Moreau envelope smoothing and specific assumptions about function properties are important considerations for determining applicability and interpreting results.

Convergence Rate

#

The convergence rate analysis is a crucial aspect of the research paper, determining the algorithm’s efficiency. The authors establish a state-of-the-art non-asymptotic convergence rate of O(ε⁻⁴) for their proposed single-loop stochastic algorithm (SMAG). This is a significant improvement over existing double-loop methods that achieve the same rate, demonstrating the algorithm’s efficiency and practical applicability. The analysis addresses the challenges of non-smoothness and non-convexity inherent in the problem, providing a rigorous theoretical foundation for the algorithm’s performance. Key to their approach is the use of Moreau envelope smoothing, enabling the application of gradient descent methods. The analysis rigorously bounds the gradient estimation error, leveraging the fast convergence properties of strongly convex/concave problems to justify single-step updates. The convergence results are extended to cover the special cases of Difference-of-Weakly-Convex (DWC) and Weakly-Convex-Strongly-Concave (WCSC) min-max optimization problems, demonstrating the algorithm’s broad applicability.

PU Learning Test

#

A PU learning test within a research paper would likely involve evaluating a model’s performance on a dataset with positive and unlabeled examples. The core challenge is the lack of negative labels, requiring techniques to estimate the class distribution or leverage other information to train and assess the model effectively. A robust test would compare the model against strong baselines, such as those using only positive data or incorporating assumptions about class proportions. Metrics should go beyond simple accuracy, focusing on precision, recall, and F1-score. Careful consideration of the experimental setup is crucial: controlling for factors like data split, positive/unlabeled ratio, and model hyperparameter tuning would help to establish reliable results. Furthermore, analysis of the model’s behavior on different subsets of the data, such as those with varying positive proportions, would provide useful insights and a more holistic view of its strengths and weaknesses.

Fairness in AUC

#

Fairness within the context of Area Under the ROC Curve (AUC) is a crucial consideration, especially in applications with societal impact. Standard AUC optimization might inadvertently perpetuate or exacerbate existing biases present in the data, leading to unfair or discriminatory outcomes for certain groups. Fairness-aware AUC optimization methods aim to mitigate such biases by incorporating fairness constraints or metrics directly into the AUC optimization process. This could involve modifying the objective function to penalize models that exhibit disparate performance across different demographic groups, or by using fairness-aware loss functions. Algorithmic approaches might include incorporating adversarial training or incorporating fairness metrics alongside AUC to obtain a Pareto-optimal solution. Data preprocessing techniques might also be employed to mitigate bias before training. The challenge lies in balancing the goal of high AUC performance with fairness considerations; some level of trade-off is often unavoidable. Careful consideration must be given to the selection of appropriate fairness metrics, and the evaluation of fairness should be performed using multiple and potentially conflicting criteria, rather than a single metric. The interpretability of the fairness-aware model is also crucial for understanding and building trust in the system’s decisions.

More visual insights

#

More on tables

🔼 This table compares different stochastic methods used to solve non-convex, non-smooth min-max problems. It contrasts their smoothness assumptions, complexity, and number of loops (single vs. double). The objective function’s structure is also detailed (weakly-convex, strongly-concave, etc.).

read the caption

Table 2: Comparison with existing stochastic methods for solving non-convex non-smooth min-max problems. The objective function is in the form of f(x,y) = f(x,y)-g(y)+h(x). NS and S stand for non-smooth and smooth respectively, and NSP means non-smooth and its proximal mapping is easily solved. WC, C stand for weakly-convex and convex respectively. WCSC stands for weakly-convex-strongly-concave, SSC stands for smooth and strongly concave and WCC means weakly-convex-concave. Note that Epoch-GDA and SMAG studies the general formulation (x, y) = f(x, y).

🔼 This table compares the proposed single-loop stochastic algorithm SMAG with existing double-loop stochastic methods for solving Difference-of-Weakly-Convex (DWC) problems. It highlights the smoothness assumptions on the component functions (φ, ψ), the complexity in terms of the convergence rate (O(ε^-k)), and the number of loops (single vs. double). SMAG stands out for achieving a state-of-the-art rate with a single loop, unlike other methods that require nested loops.

read the caption

Table 1: Comparison with existing stochastic methods for solving DWC problems with non-asymptotic convergence guarantee. * The method SBCD is designed to solve a problem in the form of min {min, φ(x, y) – minz f(x, z)} with a specific formulation of φ and ψ. However, the method and analysis can be generalized to solving non-smooth DWC problems.

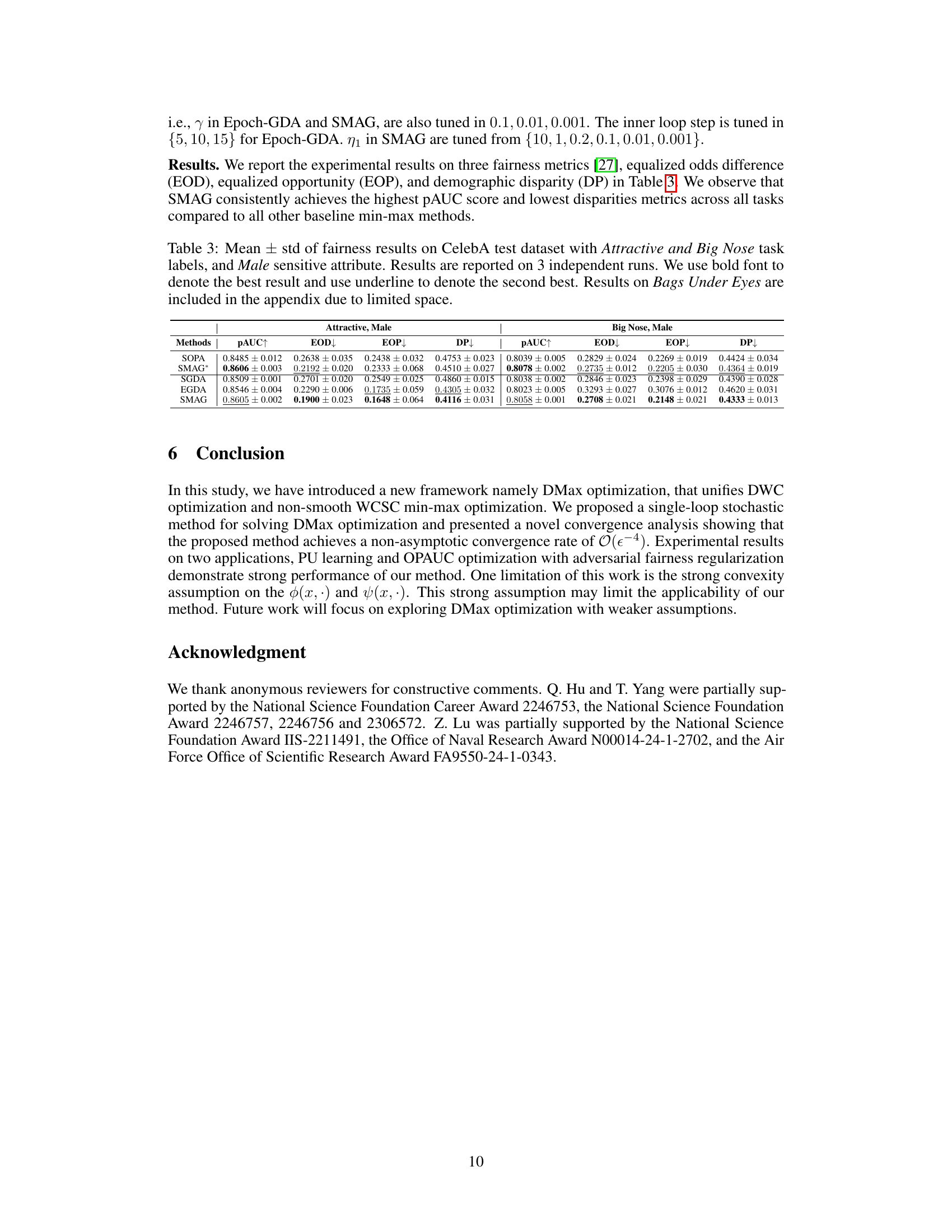
🔼 This table shows the fairness results on the CelebA test dataset for Attractive and Big Nose tasks. The results are presented as mean ± standard deviation and calculated from 3 independent runs. The best and second-best results are highlighted in bold and underlined, respectively. Due to space constraints, the results for Bags Under Eyes are included in the appendix.

read the caption

Table 3: Mean ± std of fairness results on CelebA test dataset with Attractive and Big Nose task labels, and Male sensitive attribute. Results are reported on 3 independent runs. We use bold font to denote the best result and use underline to denote the second best. Results on Bags Under Eyes are included in the appendix due to limited space.

🔼 This table presents the performance comparison of different methods on CelebA test dataset for fairness in binary classification tasks of Attractive and Big Nose. The metrics used are pAUC (Partial Area Under the ROC Curve), EOD (Equalized Odds Difference), EOP (Equalized Opportunity), and DP (Demographic Parity). Results are averaged over three independent runs, with the best result shown in bold and the second-best underlined.

read the caption

Table 3: Mean ± std of fairness results on CelebA test dataset with Attractive and Big Nose task labels, and Male sensitive attribute. Results are reported on 3 independent runs. We use bold font to denote the best result and use underline to denote the second best. Results on Bags Under Eyes are included in the appendix due to limited space.

Full paper

#