TL;DR#
Interaction-Grounded Learning (IGL) is a powerful framework for reward maximization through interaction with an environment and observing reward-dependent feedback. However, existing IGL algorithms struggle with personalized rewards, which are context-dependent feedback, lacking theoretical guarantees. This significantly limits real-world applicability.
This paper introduces the first provably efficient algorithms for IGL with personalized rewards. The key innovation is a novel Lipschitz reward estimator that effectively underestimates the true reward, ensuring favorable generalization properties. Two algorithms, one based on explore-then-exploit and the other on inverse-gap weighting, are proposed and shown to achieve sublinear regret bounds. Experiments on image and text feedback data demonstrate the practical value and effectiveness of the proposed methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on interaction-grounded learning (IGL) and personalized reward systems. It provides the first provably efficient algorithms for IGL with personalized rewards, a significant advancement over existing methods that lack theoretical guarantees. The work opens up new avenues for research in reward-free learning settings common in various applications, such as recommender systems and human-computer interaction. The introduction of a Lipschitz reward estimator is a major methodological contribution with broad applicability.
Visual Insights#
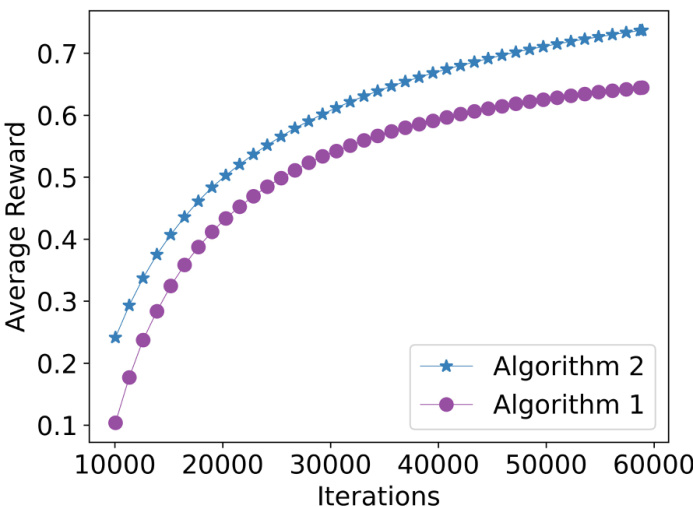
🔼 This figure shows the average reward over time for both Algorithm 1 (off-policy) and Algorithm 2 (on-policy) on the MNIST dataset. The x-axis represents the number of iterations, and the y-axis represents the average reward. Algorithm 1 starts with a lower average reward because it uses uniform exploration for the first 10,000 rounds, resulting in an average reward of approximately 0.1 (1/number of classes). Algorithm 2 demonstrates a consistently higher average reward, indicating better performance.
read the caption
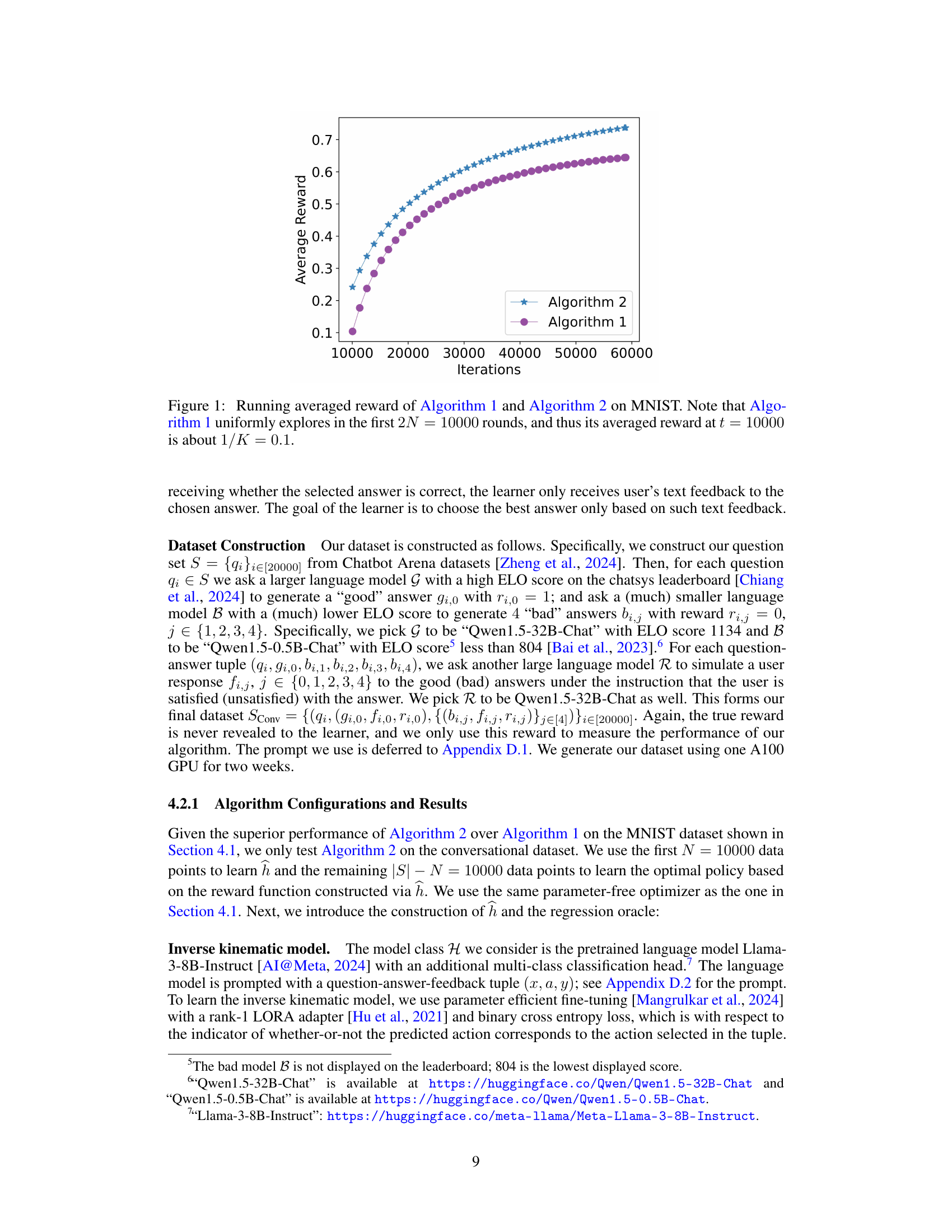
Figure 1: Running averaged reward of Algorithm 1 and Algorithm 2 on MNIST. Note that Algorithm 1 uniformly explores in the first 2N = 10000 rounds, and thus its averaged reward at t = 10000 is about 1/K = 0.1.

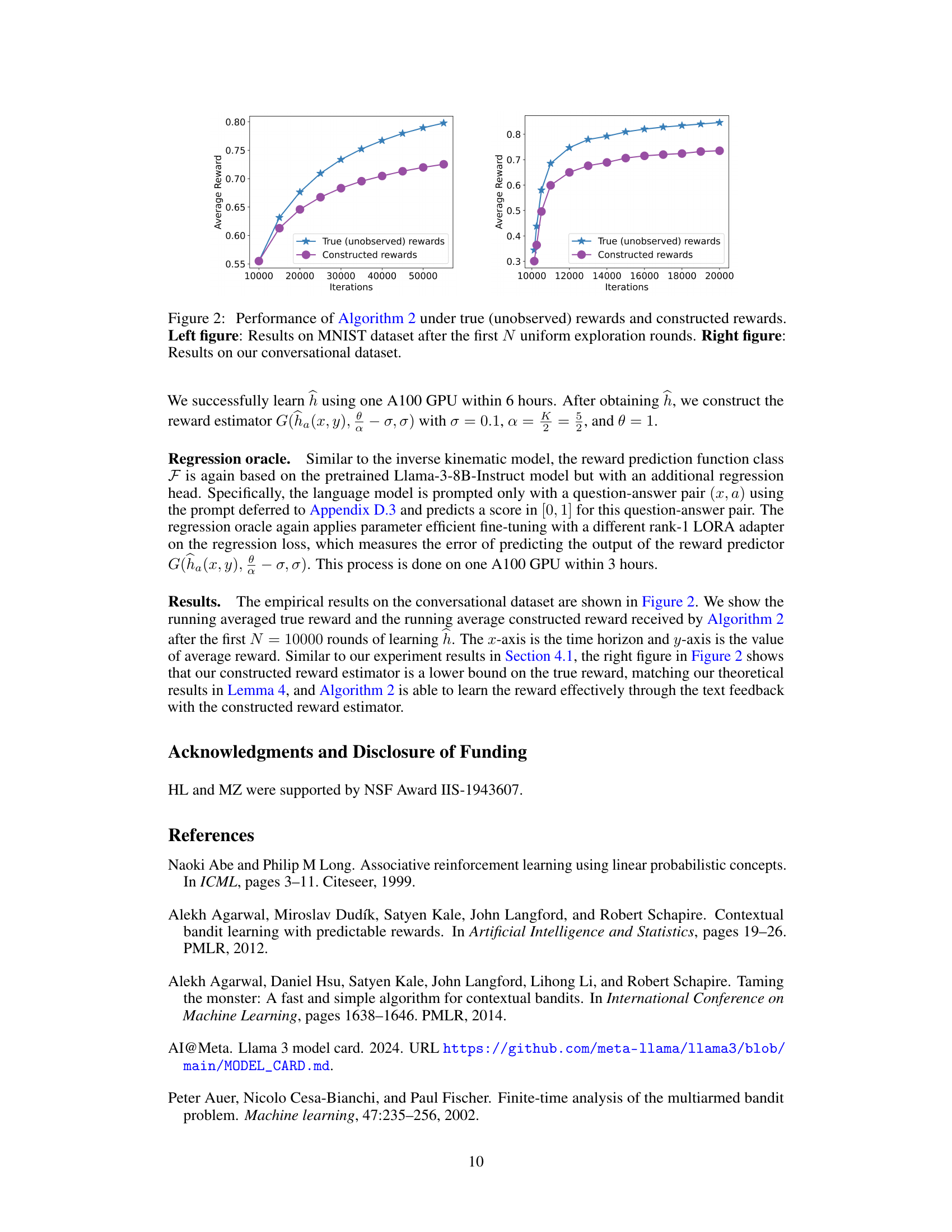
🔼 This table presents the performance comparison of two algorithms (Off-policy Algorithm 1 and On-policy Algorithm 2) on the MNIST dataset. The performance is evaluated using two metrics: Average Progressive Reward and Test Accuracy. Each algorithm is tested with two different reward estimators: Binary and Lipschitz. The numbers represent the mean and standard deviation (in parentheses) across multiple runs.
read the caption
Table 1: Performance of Algorithm 1 and Algorithm 2 on the MNIST dataset.
Full paper#