↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Label noise, errors in datasets’ labels, significantly impacts machine learning model accuracy. Existing methods often rely on assumptions about the relationship between noise transition matrices (which capture how clean labels transition into noisy ones), across different instances. These assumptions are often hard to justify and can hurt estimation accuracy.
This work proposes a novel approach. Instead of relying on assumptions, it learns the underlying latent causal structure governing how noisy labels are generated. By modeling causal relations between variables, the method implicitly captures relationships between transition matrices. This allows for more accurate estimations, especially in real-world scenarios where predefined similarities may not hold. Experiments show significantly improved classification accuracy compared to existing techniques, validating the effectiveness of the proposed approach.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on label noise learning. It introduces a novel approach to model label noise that is more accurate and robust than existing methods. The method directly addresses the limitations of similarity-based assumptions, which are hard to validate, leading to improved classification accuracy and a better understanding of the data-generating process. This opens new avenues for researching latent causal structures in noisy datasets and improves the performance of label-noise learning algorithms.
Visual Insights#

This figure shows two examples from the CIFAR-10N dataset. Both images are mislabeled as ‘Dog’ but their true labels are ‘Cat’. The purpose of this figure is to illustrate that similar images (in this case, both containing cats with fur) might be mislabeled in the same way, implying a relationship between the noise transition matrices of these similar images. This relationship is not explicitly defined but is rather implicitly captured by learning the latent causal structure.

This table compares the classification accuracy of three models on the CIFAR-10 dataset with instance-dependent label noise at different noise rates (10%, 20%, 30%, 40%, 50%). The models compared are CausalNL (original), CausalNL’ (with the proposed generative model), InstanceGM (original), and InstanceGM’ (with the proposed generative model). The results demonstrate the improvement in accuracy achieved by replacing the original generative models of CausalNL and InstanceGM with the proposed generative model in this paper.
In-depth insights#
Latent Causal Modeling#
Latent causal modeling, in the context of this research paper, addresses the challenge of learning accurate representations from noisy data by explicitly considering underlying causal relationships. Instead of relying on potentially inaccurate assumptions about the noise distribution, this approach models the data generation process, uncovering latent causal variables that influence both the observed features and the noisy labels. This technique has several advantages: it avoids making strong assumptions about data similarity or manifold structures; it offers a more robust and interpretable method for estimating noise transition matrices; and it directly addresses the root causes of the noise, leading to improved classification accuracy. The learnable graphical model employed in this approach captures complex causal dependencies between latent variables, providing a more realistic representation of real-world data generation. However, the method’s reliance on additional supervised information for learning the causal structure is a limitation, as it requires access to clean samples that are often unavailable in practice.
Generative Label Noise#
Generative label noise models offer a powerful paradigm shift in addressing the challenges of noisy labels in machine learning. Instead of treating noise as a post-hoc corruption process, these models directly embed noise generation mechanisms within the data generation process itself. This approach is particularly beneficial as it allows for more realistic modeling of noise characteristics, moving beyond simplistic assumptions like symmetric or class-conditional noise. By explicitly modeling how clean labels transform into noisy ones, generative methods enable more sophisticated and accurate estimations of clean label distributions. This leads to improved robustness and performance of subsequent machine learning models, even in scenarios with high label noise rates. The core strength lies in leveraging the underlying structure of noise generation for more effective label correction and improved generalization. However, the complexity of designing and training these models can be significantly higher compared to simpler methods, potentially requiring large-scale datasets and computational resources. Furthermore, identifiability of model parameters presents a key theoretical challenge. The success of a generative approach hinges on the accuracy of the model in representing the real-world noise process; inaccurate modeling can lead to poorer results than simpler, more readily-trained alternatives. Therefore, careful consideration of model design and thorough empirical validation are critical.
Causal Structure Learning#
Causal structure learning, in the context of label noise modeling, offers a powerful paradigm shift from traditional similarity-based approaches. Instead of relying on often-unrealistic assumptions about the relationships between noise transition matrices, this method focuses on uncovering the underlying causal mechanisms that generate the noisy labels. By learning a graphical model representing these causal relationships, the algorithm implicitly captures the dependencies between different instances’ noise characteristics. This allows for a more accurate and robust estimation of noise transition matrices, even when dealing with complex real-world data where simple similarity assumptions break down. A key advantage lies in the ability to generalize to unseen instances by leveraging the learned causal structure, leading to improved classification accuracy and robustness in the presence of label noise. The framework’s strength lies in its ability to handle instance-dependent label noise scenarios where standard techniques fail. The use of latent causal variables is particularly valuable in capturing nuanced relationships, resulting in more accurate and generalizable models. This approach directly addresses the limitations of similarity-based methods by providing a principled and data-driven way to understand and model label noise.
Noise Transition Estimation#
Accurate noise transition matrix estimation is crucial for effective label noise learning. The challenge lies in accurately estimating the probability of a noisy label given a clean label for each instance, especially when only noisy data is available. Methods often rely on assumptions, such as instance-independent noise or similarity-based relations between instances. Learning the latent causal structure underlying the noisy label generation process offers a powerful alternative, avoiding restrictive similarity assumptions. By modeling causal relationships between latent variables and the observed noisy labels, we can implicitly capture the relationships between noise transition matrices across different instances, leading to more accurate estimation even with limited data. The effectiveness of this approach depends on accurately learning this causal structure and leveraging it to infer missing transition matrix information. This represents a significant advance towards robust and accurate label noise modeling, ultimately improving classification performance in noisy settings.
Future Research#
Future research directions stemming from this work on latent causal structure for label noise modeling could focus on several key areas. Extending the model to handle more complex causal relationships beyond the linear assumptions made in this paper is crucial for broader applicability. This could involve investigating non-linear causal discovery methods or exploring more advanced graphical models. Investigating the impact of different noise distributions and exploring methods for automatically detecting and adapting to various noise patterns would improve robustness. Further exploration of the semi-supervised aspect is important, potentially focusing on more efficient techniques for selecting clean examples or incorporating techniques that can leverage unlabeled data more effectively. Finally, applying the approach to other challenging machine learning domains where noisy labels are common, such as medical image analysis or natural language processing, would demonstrate its wider impact and reveal potential limitations.
More visual insights#
More on figures

This figure compares two different data-generating processes for noisy labels. (a) shows a model where the instance X directly causes the noisy label Ỹ. This model is considered insufficient because in many datasets (images, videos etc.), there are often latent variables (like shape or color) that are the direct cause of the label, rather than the perceptual data itself. (b) Shows the model proposed in the paper, where latent variables Z and S generate the instance X, while Z also generates the noisy label Ỹ. This structure captures the latent factors that cause mislabeling more effectively.
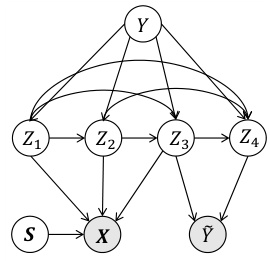
This figure illustrates the data generating process used in the CSGN model. It shows a directed acyclic graph (DAG) representing the causal relationships between latent variables and observed variables. There are four latent causal variables (Z1, Z2, Z3, Z4) with directed edges indicating causal influence. These variables are influenced by the clean label (Y) and also influence each other. The latent noise variables (N1, N2, N3, N4) introduce randomness into the generation of these causal variables. There is an additional latent variable S that is independent of the clean label and affects the generation of the observed instance X. The noisy label Ỹ is generated by Z1, Z2, Z3, Z4, and influenced by Y. The solid arrows represent causal influences, and the shaded nodes represent observed variables.

This figure shows a directed acyclic graph (DAG) representing the data generating process. The observed instance X and noisy label Ỹ are generated by subsets of latent causal variables Z, which have causal dependencies among them. The variables S are other variables not influenced by the clean label Y. The arrows indicate the causal direction, showing how the variables influence each other, while the blue arrow indicates the edge weights vary with the clean label Y. This highlights the instance-dependent nature of noise transition matrices.
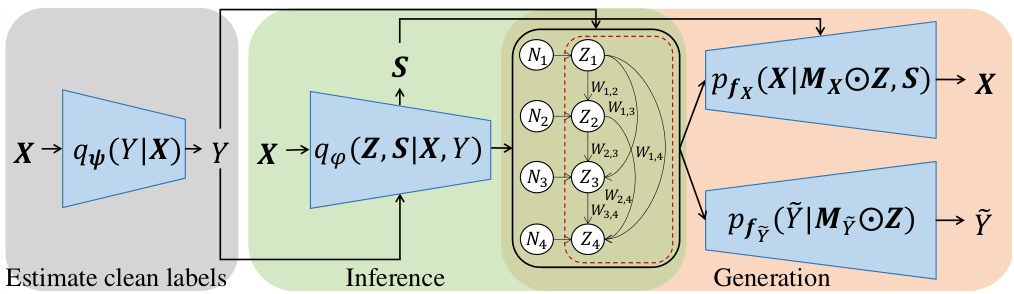
This figure illustrates the workflow of the CSGN (Causal Structure for the Generation of Noisy Data) method. It’s broken down into three stages: 1. Estimate clean labels: A classification network, qψ(Y|X), takes an instance (X) as input and outputs the estimated clean label (Y). 2. Inference: An encoder, qθ(Z, S|X, Y), takes the instance (X) and the estimated clean label (Y) to infer the latent causal variables (Z) and other variables unrelated to the clean label (S). 3. Generation: Two decoders, pfx(X|Mx⊙Z, S) and pfy(Ỹ|My⊙Z), utilize the latent causal variables (Z) and S, masked by Mx and My respectively, to generate the instance (X) and noisy label (Ỹ). The masks, Mx and My, select the appropriate subset of causal variables Z for generating each part. The process is designed to model how the latent causal structure influences both the instance and the resulting noisy label.

This figure shows the estimation error of noise transition matrices for four different datasets (MNIST, Fashion-MNIST, CIFAR-10, and CIFAR-100) using three different methods (CSGN, BLTM, and MEIDTM). The x-axis represents the noise rate, and the y-axis represents the estimation error. The error bars indicate the standard deviation. The results show that CSGN generally has a lower estimation error compared to BLTM and MEIDTM across all datasets and noise rates.

This figure displays the estimation error of noise transition matrices for four different datasets (MNIST, Fashion-MNIST, CIFAR-10, and CIFAR-100) using instance-dependent label noise. The x-axis represents the noise rate, ranging from 0.1 to 0.5. The y-axis represents the estimation error. Each dataset has its own subplot, showing how the estimation error changes with increasing noise rate. Error bars indicating standard deviations are included for each data point. The figure visually compares the performance of the proposed method to other approaches for estimating noise transition matrices under different noise levels.

This figure shows the results of a sensitivity analysis testing the effect of varying the number of causal variables (Z) on the test accuracy of a model trained on the CIFAR-10 dataset with instance-dependent label noise at a rate of 0.5. The x-axis represents the number of causal variables, while the y-axis represents the test accuracy. Error bars indicate the standard deviation. The graph shows that the model’s performance is relatively insensitive to the number of causal variables within the tested range.
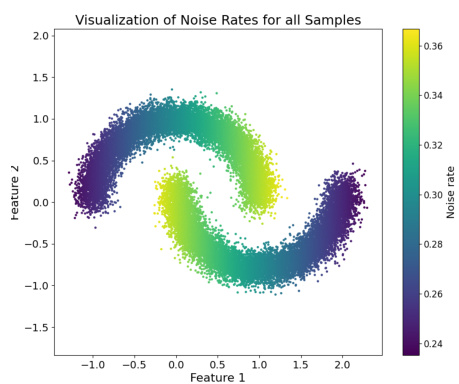
This figure shows a scatter plot of a synthetic dataset used in the paper’s experiments. The x-axis represents Feature 1, and the y-axis represents Feature 2. Each point is colored according to its associated noise rate, which is calculated as a function of Feature 2. The color gradient ranges from dark purple (low noise rate) to bright yellow (high noise rate). The data forms a two-armed spiral shape, indicating that the noise rate varies systematically across the dataset, rather than being randomly distributed. This specific dataset is used to evaluate the model’s ability to learn the latent causal structure underlying the noise generation process, focusing on how the noise rate is linked to specific features within the data.

This figure uses t-SNE to visualize the similarity of learned noise transition matrices by CSGN and MEIDTM. It compares the distances between pairs of data points with the same predicted clean labels. The key observation is that the distances between these pairs differ significantly between the two methods, indicating that CSGN learns a different similarity structure compared to MEIDTM, which is based on instance-dependent transition matrices.
More on tables

This table presents the classification accuracy results on the CIFAR-100 dataset. The original CausalNL and InstanceGM methods are compared to modified versions (CausalNL’ and InstanceGM’) where the generative model has been replaced with the proposed model from the paper. The results are shown for different noise rates (IDN-10%, IDN-20%, IDN-30%, IDN-40%, IDN-50%), demonstrating the improved performance of the modified methods. The numbers represent the average accuracy and standard deviation across multiple trials.
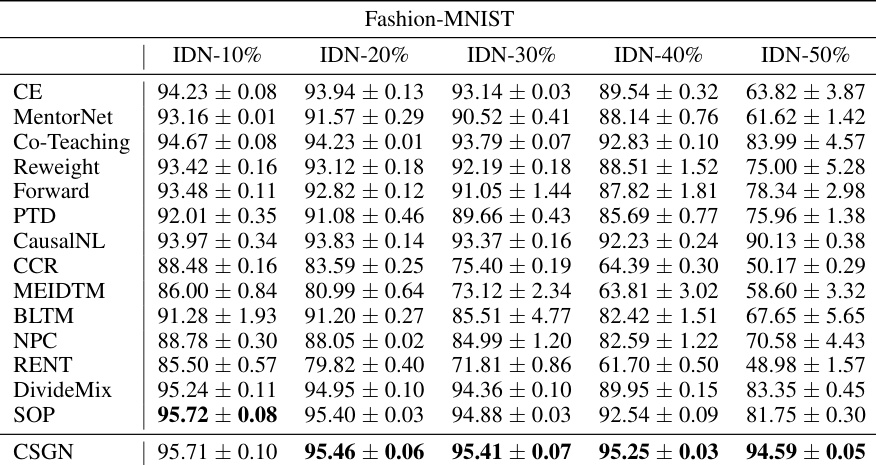
This table presents the classification accuracy results on the Fashion-MNIST dataset with different levels of instance-dependent label noise (IDN). The results are shown for five different noise rates (10%, 20%, 30%, 40%, and 50%). Multiple methods are compared, including the proposed CSGN method and several baselines (CE, MentorNet, Co-Teaching, Reweight, Forward, PTD, CausalNL, CCR, MEIDTM, BLTM, NPC, RENT, DivideMix, and SOP). The mean accuracy and standard deviation are reported for each method and noise level. This allows for a comparison of the performance of different algorithms in handling label noise at varying levels of severity.
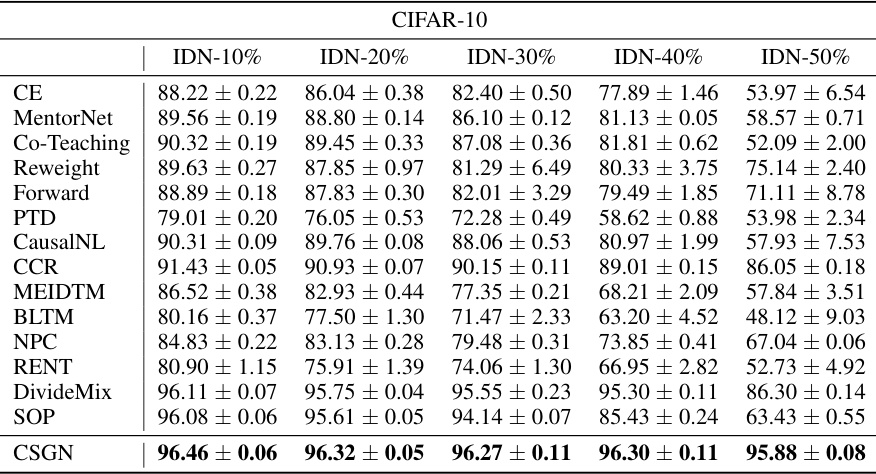
This table presents the mean and standard deviation of classification accuracy for different label noise methods on the CIFAR-10 dataset. The results are broken down by different levels of label noise (IDN-10% to IDN-50%), allowing for a comparison of method performance under varying noise conditions. The table includes results for several baselines as well as the proposed CSGN method.
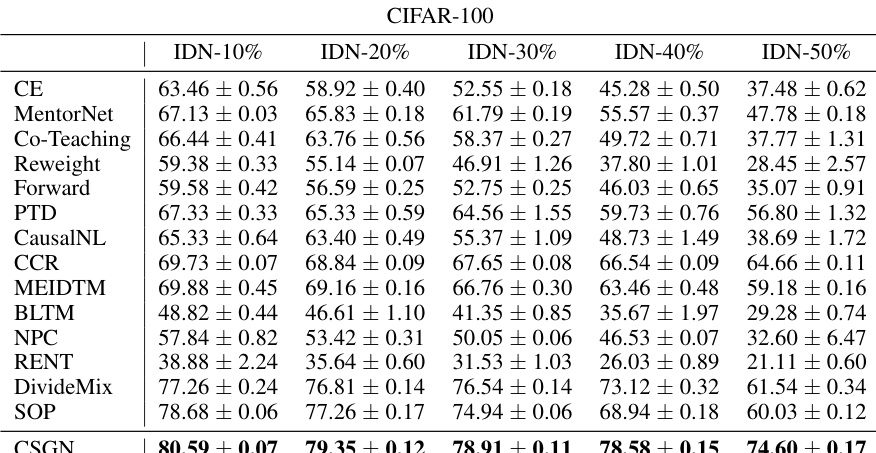
This table presents the classification accuracy results on the CIFAR-100 dataset under different instance-dependent label noise levels (IDN-10%, IDN-20%, IDN-30%, IDN-40%, IDN-50%). The performance of several methods, including the proposed CSGN method, is compared against various baseline approaches. The mean and standard deviation of the accuracy are reported for each method and noise level. This allows for a quantitative comparison of how well different approaches handle varying levels of noisy labels in the CIFAR-100 image classification task.

This table presents the mean and standard deviation of classification accuracy for different methods on the CIFAR-N dataset. CIFAR-N is a real-world dataset with various types and rates of label noise. The results are broken down by noise type (Worst, Aggregate, Random 1, Random 2, Random 3, Noisy) and show how each method performs under different noise conditions.
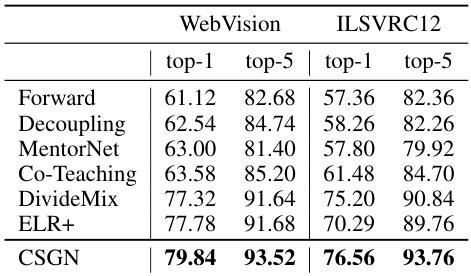
This table presents the top-1 and top-5 accuracy results of the CSGN model and several baseline methods on the WebVision validation set and the ImageNet ILSVRC12 validation set. It showcases the performance comparison on a real-world, large-scale image dataset, demonstrating CSGN’s effectiveness in handling noisy labels and achieving state-of-the-art results.

This table presents the results of an ablation study comparing the performance of the CSGN model with and without a semi-supervised learning warmup phase. The study investigates the impact of removing the semi-supervised learning warmup from the CSGN method, replacing it with a regular early-stopping approach instead. The results show that the CSGN model retains effectiveness even without the semi-supervised learning warmup.

This table presents the results of an ablation study conducted on the CIFAR-10 dataset to evaluate the impact of removing the ELBO loss and the L_M regularization term from the CSGN model. The table compares the performance of four different model variations: the full CSGN model, a model without the ELBO loss, a model without the L_M loss, and a model without both losses. The performance is measured using accuracy on the CIFAR-10 dataset under different levels of instance-dependent label noise (IDN). The results show the effect of each loss term on model performance.

This table presents a comparison of classification accuracy on the CIFAR-10 dataset using three different methods: PES, CSGN-PES, and CSGN. The methods are evaluated under different levels of instance-dependent label noise (IDN). CSGN-PES represents a variant of CSGN that utilizes the PES algorithm for sample selection and training. The results show how each method performs with varying amounts of label noise, demonstrating the effectiveness of the CSGN approach in handling noisy labels.

This table shows the number and accuracy of the selected clean samples for CIFAR-10 dataset under different noise levels (IDN-10%, IDN-20%, IDN-30%, IDN-40%, IDN-50%). The results demonstrate that the method is effective in selecting a large number of clean samples with high accuracy, even with increasing noise.

This table presents the number and accuracy of clean samples selected from the CIFAR-100 dataset using the proposed method. The results are categorized by different noise levels (IDN-10%, IDN-20%, IDN-30%, IDN-40%, and IDN-50%). The number of samples varies with the noise level, with a decrease as noise increases, and high accuracy (above 98%) is maintained except at the highest noise rate.

This table presents the classification accuracy results for different methods on the CIFAR-10 dataset with varying instance-dependent label noise ratios (IDN). The results are averaged over multiple trials, with standard deviations reported to indicate the reliability of the results. ‘CE-clean’ represents the performance of a classifier trained on the clean CIFAR-10 dataset, serving as a baseline. The other methods represent various label noise learning techniques, demonstrating their comparative performance against the baseline and each other.

This table presents the mean and standard deviation of classification accuracy for CIFAR-100 using different methods under different label noise rates (IDN-10%, IDN-20%, IDN-30%, IDN-40%, IDN-50%). The results are compared against the performance on clean data (CE-clean) and the proposed method (CSGN).
Full paper#