↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world problems rely on solving Boolean satisfiability (SAT) problems. However, deep learning approaches to improve SAT solving are hampered by a lack of large, realistic datasets. Existing datasets are limited or randomly generated, failing to capture the complexities of real-world SAT instances.
HardCore tackles this issue by proposing a novel approach to generate challenging UNSAT problems. It leverages the concept of ‘cores’—minimal unsatisfiable subsets of clauses—to ensure generated problems retain key characteristics of real-world instances. A graph neural network accelerates core detection, enabling efficient generation of diverse and difficult problems. Experiments show HardCore significantly improves SAT solver runtime prediction compared to baselines.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with SAT solvers and machine learning for several reasons. First, it addresses the critical shortage of high-quality datasets for training deep learning models on SAT problems, which significantly hinders progress in this area. Second, it introduces a novel, fast core detection method using graph neural networks that dramatically improves upon existing techniques. Third, the proposed methodology directly contributes to better runtime prediction of SAT solvers which is highly relevant to both research and practical applications in various industries like circuit design, cryptoanalysis, and scheduling. This research opens up exciting avenues for future work including developing more sophisticated generative models for SAT problems and exploring novel data augmentation strategies.
Visual Insights#

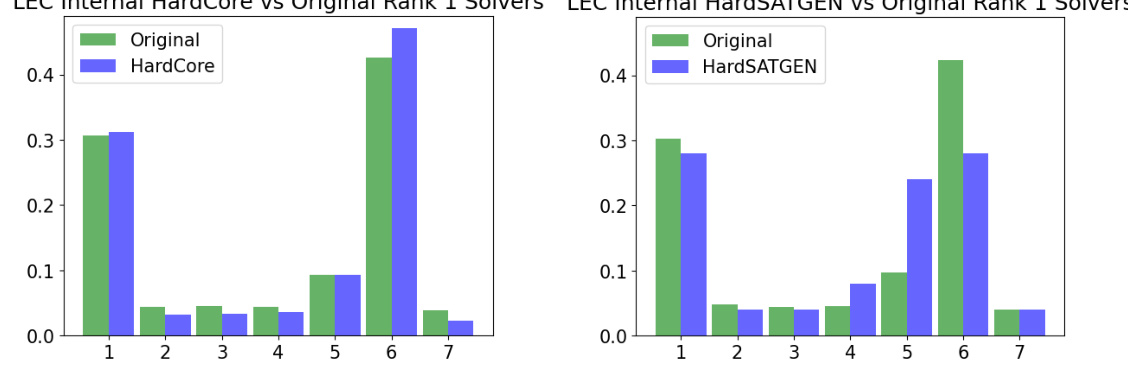
This figure compares different SAT problem generation methods in terms of their computational cost and the hardness of the generated problems. The x-axis represents the relative hardness of the generated problems compared to original problems, while the y-axis represents the time it takes to generate each problem. The plot shows that HardCore achieves the best balance between generating hard problems and computational efficiency. While HardSATGEN produces very hard problems, it has a significantly higher computational cost. In contrast, G2MILP and W2SAT are much faster but fail to generate sufficiently hard problems.

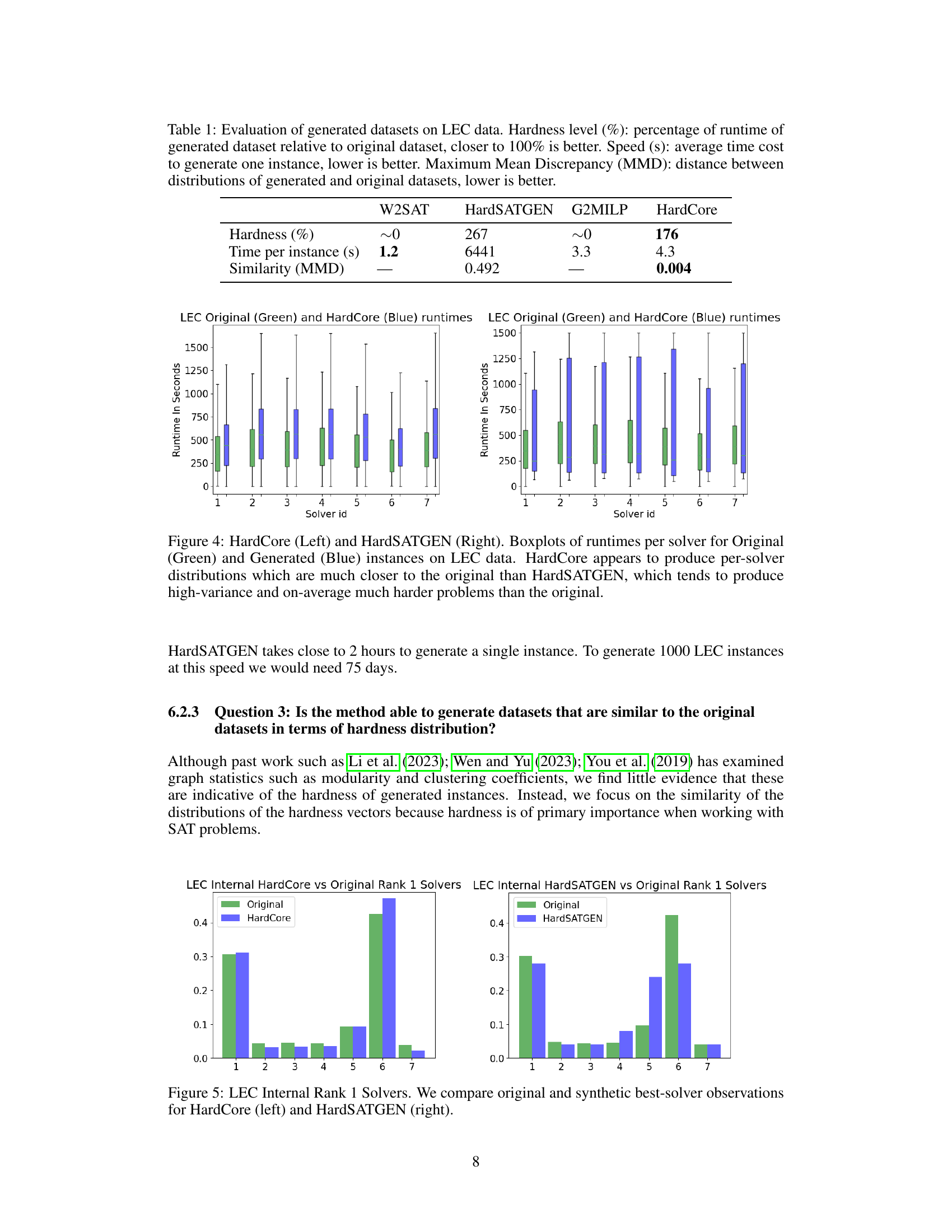
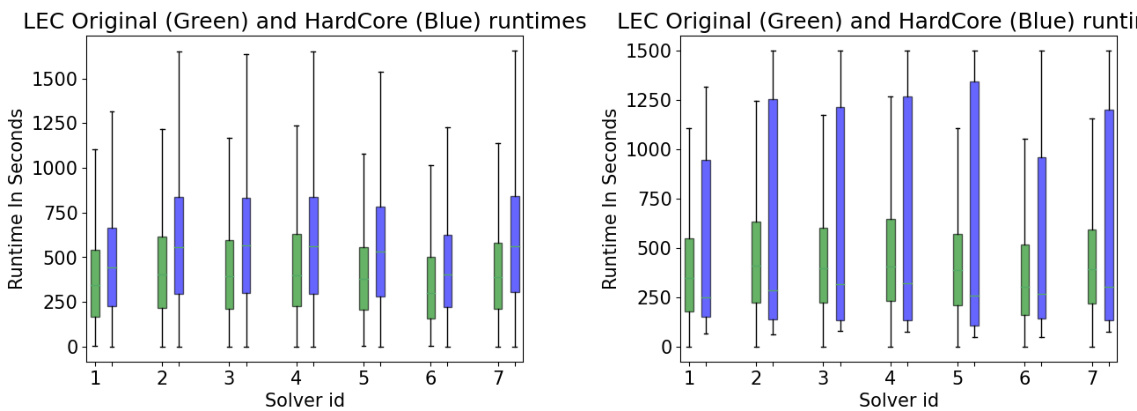
This table compares four different methods for generating synthetic SAT problem instances based on their hardness, generation speed, and similarity to real-world instances. Hardness is measured as the percentage of runtime compared to original instances; a higher percentage indicates harder instances. Speed represents the average time to generate a single instance. Finally, similarity is quantified using the Maximum Mean Discrepancy (MMD), measuring the difference in distribution between generated and original instances; a lower MMD signifies greater similarity.
In-depth insights#
HardCore SAT Gen#
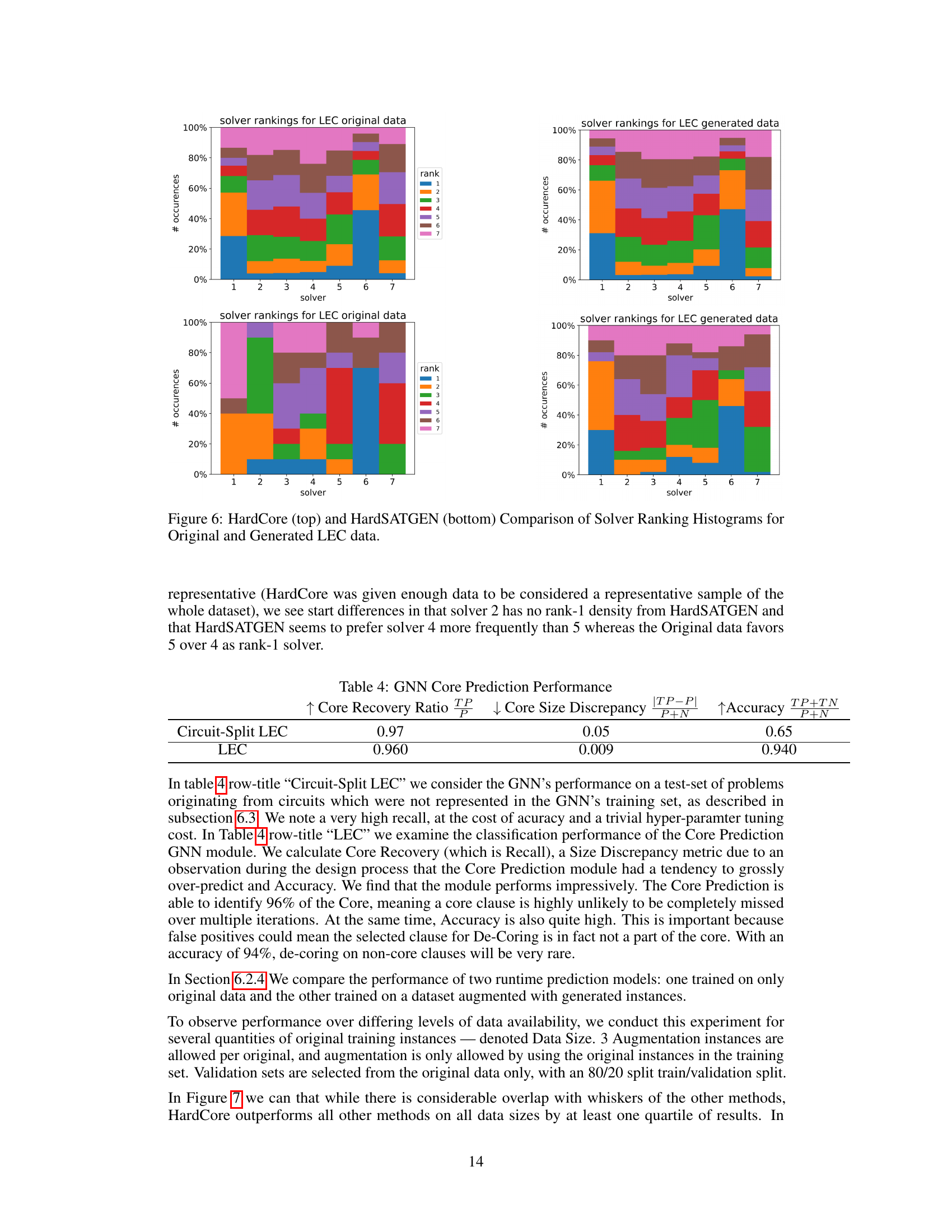
HardCore SAT Gen, as a hypothetical method, proposes a novel approach to generating challenging, unsatisfiable Boolean formulas (UNSAT). It cleverly leverages the concept of cores, minimal unsatisfiable subsets of clauses, which are fundamentally linked to a problem’s difficulty. Unlike previous methods that often struggled to produce truly hard instances or were computationally expensive, HardCore SAT Gen aims to address both limitations. The method likely involves a two-stage process: first, efficiently identifying the core of an existing UNSAT problem using a potentially fast technique like a graph neural network (GNN); second, intelligently manipulating and augmenting this core to create new, harder UNSAT problems. The core refinement process involves iteratively adding clauses while ensuring that the new problems remain difficult. The proposed solution is particularly relevant for improving the training and evaluation of machine learning models that predict SAT solver runtime. The use of a GNN for core detection is a key innovation, likely resulting in a significant speedup over traditional core-finding methods. The generated datasets are expected to be both diverse and challenging, offering a substantial improvement over existing, limited datasets.
GNN Core Detect#
A GNN Core Detect system leverages the power of graph neural networks (GNNs) to efficiently identify cores within Boolean satisfiability (SAT) problems. Speed is crucial, as traditional core detection methods are computationally expensive. The GNN learns to classify clauses as either belonging to the core or not, thereby significantly accelerating the process. Accuracy is also paramount: while the GNN may not be perfect, post-processing steps can mitigate false positives. The effectiveness of a GNN Core Detect system is demonstrated through experimental results showing that it produces a good trade-off between speed and accuracy, crucial for improving the efficiency of SAT solving and data augmentation for machine learning models.
Hardness Preserved#
The concept of “Hardness Preserved” in the context of SAT problem generation is crucial. It highlights the challenge of creating synthetic SAT instances that mirror the difficulty of real-world problems. Existing methods often fail, producing either trivially easy or unrealistically hard instances. A successful approach must cleverly balance these extremes, ensuring that the generated problems effectively challenge SAT solvers, thus allowing for robust evaluation and training of machine learning models. The core, or minimal unsatisfiable subset, of a SAT instance is directly linked to its hardness. Therefore, techniques that manipulate cores while adding carefully controlled randomness, offer a promising strategy for preserving hardness. This involves a trade-off: the ability to quickly detect cores versus the risk of inadvertently simplifying a problem. The development of efficient core detection methods using techniques like graph neural networks is key to achieving both hardness preservation and scalability. Ultimately, the value lies in creating high-quality augmented datasets enabling more effective data-driven approaches to SAT solving.
Runtime Prediction#
The research paper explores runtime prediction for Boolean satisfiability problem (SAT) solvers. Accurate runtime prediction is crucial for efficient algorithm selection and resource allocation in SAT solving. The core of the study revolves around leveraging machine learning techniques, specifically focusing on data augmentation strategies to improve the accuracy of runtime prediction models. The challenge addressed is the scarcity of large, high-quality, and realistic SAT problem datasets for training these models. The paper introduces a novel method for generating synthetic, hard SAT instances that are structurally similar to real-world problems, which in turn improves the efficacy of machine learning models for runtime prediction. The proposed approach involves identifying and manipulating the key contributors to a problem’s hardness, enabling more effective data augmentation. Fast core detection using a graph neural network is a key innovation, which addresses previous time-scalability obstacles. This data augmentation strategy demonstrably improves mean absolute error for runtime prediction compared to approaches using only randomly generated or existing, limited datasets. The results highlight the significance of carefully designed synthetic data in advancing SAT solver runtime prediction and showcase a fast, effective method for generating it.
Future Directions#
Future research could explore extending the core refinement process to SAT problems beyond UNSAT instances by focusing on backbones, the minimal set of variables assigned the same value in all satisfying assignments. Improving the GNN’s core prediction efficiency, perhaps through architectural innovations or more advanced training techniques, is crucial for scalability to larger problem instances. Investigating the impact of different core refinement strategies, beyond the literal addition method used here, is warranted. A more comprehensive analysis of solver runtime prediction, considering factors beyond total time, including specific solver performance profiles, may improve accuracy. Finally, exploring the application of this data augmentation method to other related problems in AI, like constraint satisfaction problems or logic programming, could reveal broader applicability and generate further insights.
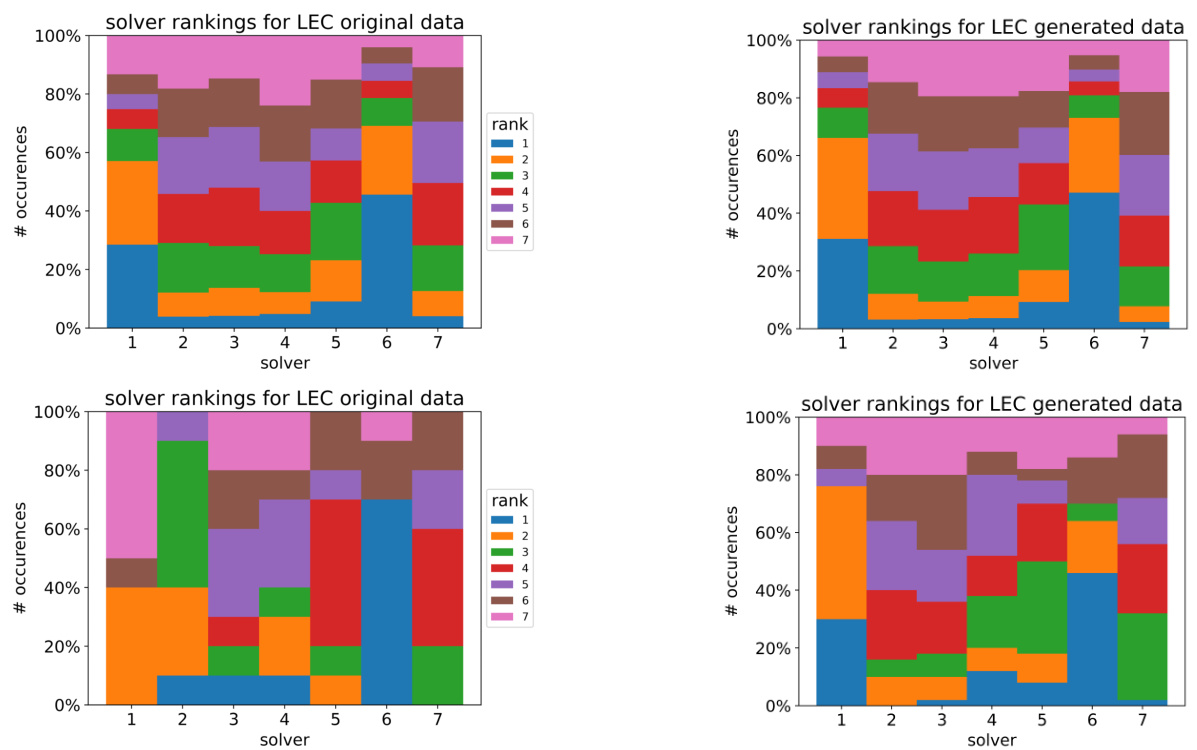
More visual insights#
More on figures

This figure illustrates the core refinement process, a two-step iterative process used to generate harder instances. First, a GNN predicts the core of a generated instance. Then, in the ‘De-coring’ step, a non-conflicting literal is added to a clause within the core. This makes the core satisfiable, leading to a new, smaller unsatisfiable subset (a harder core). The process repeats until the core is deemed sufficiently hard.
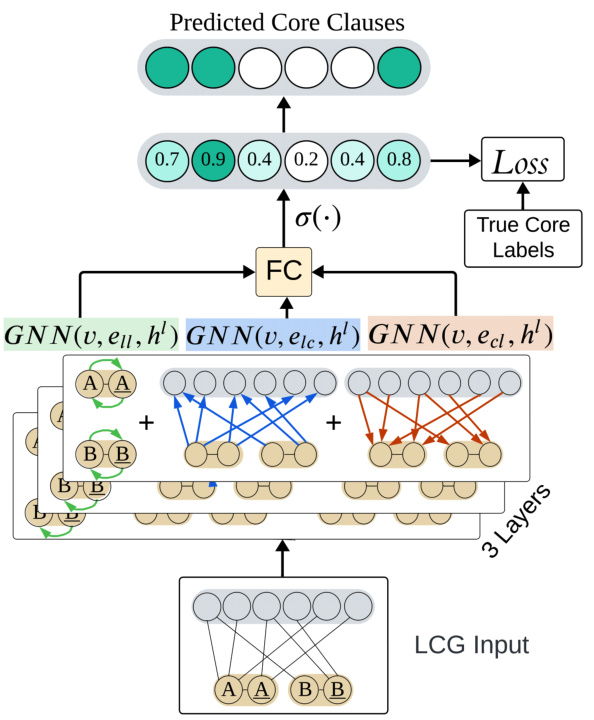
This figure illustrates the architecture of the Graph Neural Network (GNN) used for core prediction. The GNN consists of three parallel message-passing neural networks (MPNNs), each processing a different type of edge in the literal-clause graph (LCG). These MPNNs process literal-literal edges, literal-to-clause edges, and clause-to-literal edges. The outputs of these MPNNs are aggregated at each layer, and the final layer’s node embeddings are passed through a fully-connected layer with a sigmoid activation function to produce a core membership probability for each clause node. A binary classification loss (comparing predicted probabilities to true core labels) is used during training.
This figure shows a comparison of different SAT problem generation methods in terms of their inference cost (time taken to generate a problem) and the hardness of the generated problems. The x-axis represents the hardness of the generated problem instances as a percentage of the hardness of the original instances (100% represents the original hardness). The y-axis represents the inference cost per instance, measured in seconds, minutes, or hours. The figure demonstrates that the HardCore method achieves a superior balance between cost and problem hardness, generating problems that are significantly harder than those produced by other methods, at a significantly lower cost.
This figure shows a comparison of different SAT problem generation methods in terms of their computational cost (inference cost) and the hardness of the generated problems. The x-axis represents the instance hardness as a percentage of the original problem’s hardness, while the y-axis represents the time cost per instance. The plot shows that the HardCore method achieves the best balance between generating hard problems and maintaining a low computational cost. Other methods like HardSATGEN produce harder problems but at a significantly higher cost, while methods like G2MILP and W2SAT produce significantly easier problems.
The figure shows a comparison of different methods for generating hard SAT problems, plotting instance hardness against the time cost per instance. HardCore is shown to achieve the best balance between generating hard problems and having a reasonable inference cost. Other methods either generate relatively easy problems or are computationally very expensive, highlighting the efficiency of the HardCore approach.
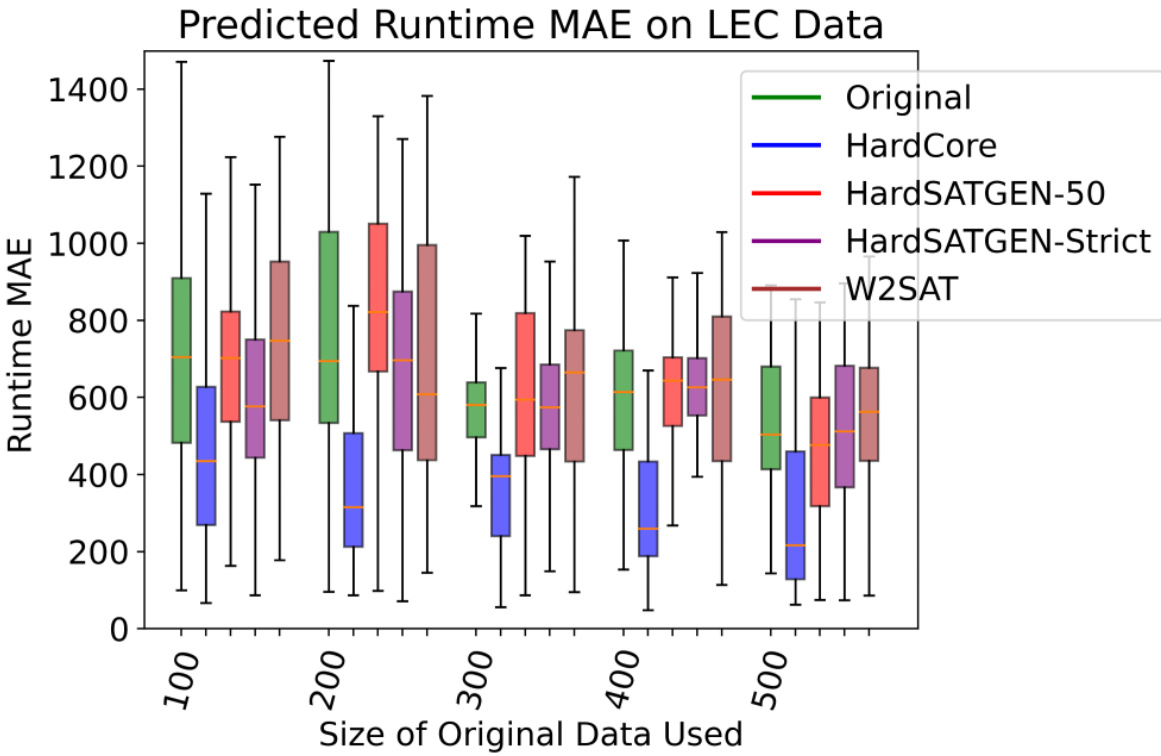
This figure shows box plots of Mean Absolute Error (MAE) for runtime prediction across different sizes of training datasets. It compares the performance of using the HardCore method for data augmentation against other methods (Original, HardSATGEN-50, HardSATGEN-Strict, W2SAT). The x-axis represents the size of the original training dataset used, and the y-axis represents the MAE. The box plots show the median, quartiles, and range of the MAE values for each method and dataset size, allowing for a visual comparison of the effectiveness of different data augmentation techniques in improving runtime prediction accuracy.
More on tables
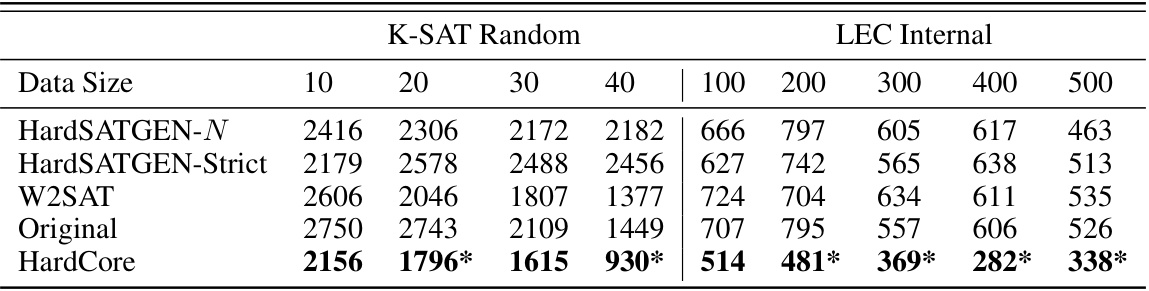
This table compares the performance of different SAT instance generation methods on a dataset of LEC (Logic Equivalence Checking) instances. It evaluates three key aspects: 1. Hardness: The percentage of the original dataset’s runtime achieved by the generated instances (closer to 100% indicates better preservation of hardness). 2. Speed: The average time taken to generate a single instance (lower is better). 3. Similarity: The Maximum Mean Discrepancy (MMD) between the distributions of generated and original instances (lower values indicate higher similarity). The table shows that HardCore achieves a good balance between hardness and speed compared to other methods.

This table presents a comparison of different SAT instance generation methods on their ability to generate hard instances similar to real-world examples, as measured by runtime and distribution similarity. It shows the hardness level (percentage of original runtime), generation speed (seconds per instance), and Maximum Mean Discrepancy (MMD) for each method, indicating their performance in creating realistic and challenging instances for machine learning.

This table presents a comparison of different SAT generation methods on a specific dataset (LEC). The comparison focuses on three key metrics: Hardness (percentage of original runtime), Speed (time to generate a single instance), and Similarity (measured by Maximum Mean Discrepancy, or MMD, between the generated and original data distributions). Lower MMD indicates greater similarity. The table helps assess the efficiency and quality of each generation method in terms of producing instances that are both challenging (hard) and similar to real-world problems.

This table presents a comparison of different SAT generation methods on LEC data. It evaluates three key metrics: Hardness (the percentage of runtime of generated problems relative to original problems), Speed (the average time needed to generate a single instance), and Similarity (measured by Maximum Mean Discrepancy, a lower value indicating greater similarity between the generated and original dataset distributions).

This table presents the Mean Absolute Error (MAE) of runtime prediction for different dataset sizes, averaged across seven solvers and fifteen trials. The data shows the MAE for runtime prediction models trained on both original data and data augmented with the HardCore method. The Wilcoxon signed-rank test was used to determine statistical significance (p<0.05) between HardCore augmented data and the original data, with asterisks marking statistically significant improvements. A supplementary figure provides a box plot visualization of the results.

This table presents the Mean Absolute Error (MAE) of runtime prediction for different training data sizes using the HardCore method and the original data. It shows that using HardCore-augmented data leads to lower MAE compared to using only the original data.
Full paper#