TL;DR#
Self-supervised learning (SSL) aims to learn data representations without labeled data. While invariant SSL (I-SSL) methods have achieved success, they often sacrifice useful features. Equivariant SSL (E-SSL) addresses this by learning features sensitive to data augmentations, but lacks theoretical understanding. This paper tackles this gap by focusing on the simplest rotation prediction method.
This research uses an information-theoretic perspective to analyze E-SSL’s generalization ability. It reveals a critical synergy effect where learning class-relevant features improves equivariant prediction, which in turn benefits downstream tasks. The study establishes theoretical principles for effective E-SSL design, encompassing lossy transformations, class relevance, and shortcut pruning. It further uncovers model equivariance as a key factor to improve performance.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides a much-needed theoretical framework for understanding equivariant self-supervised learning (E-SSL), a rapidly growing field. It addresses the current lack of theoretical understanding in E-SSL by introducing an information-theoretic perspective. This offers valuable guidance for designing more effective E-SSL methods, paving the way for advancements in self-supervised learning.
Visual Insights#
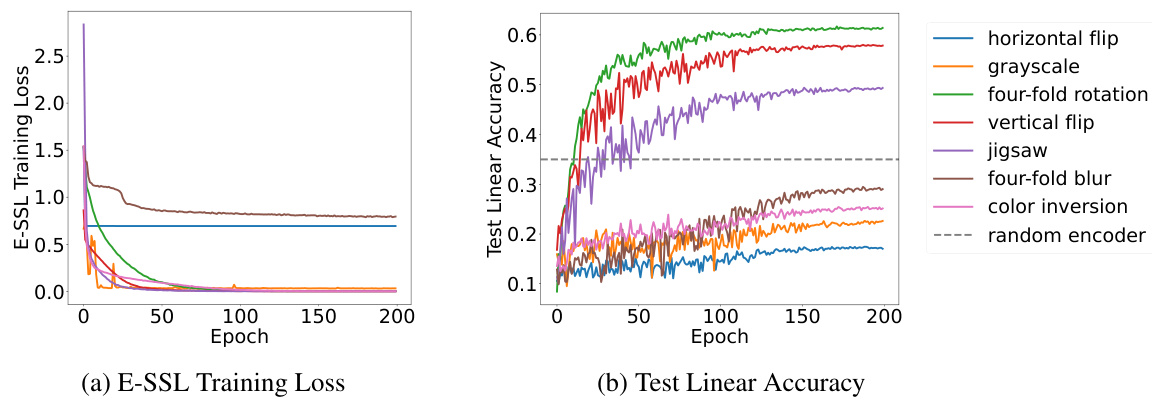
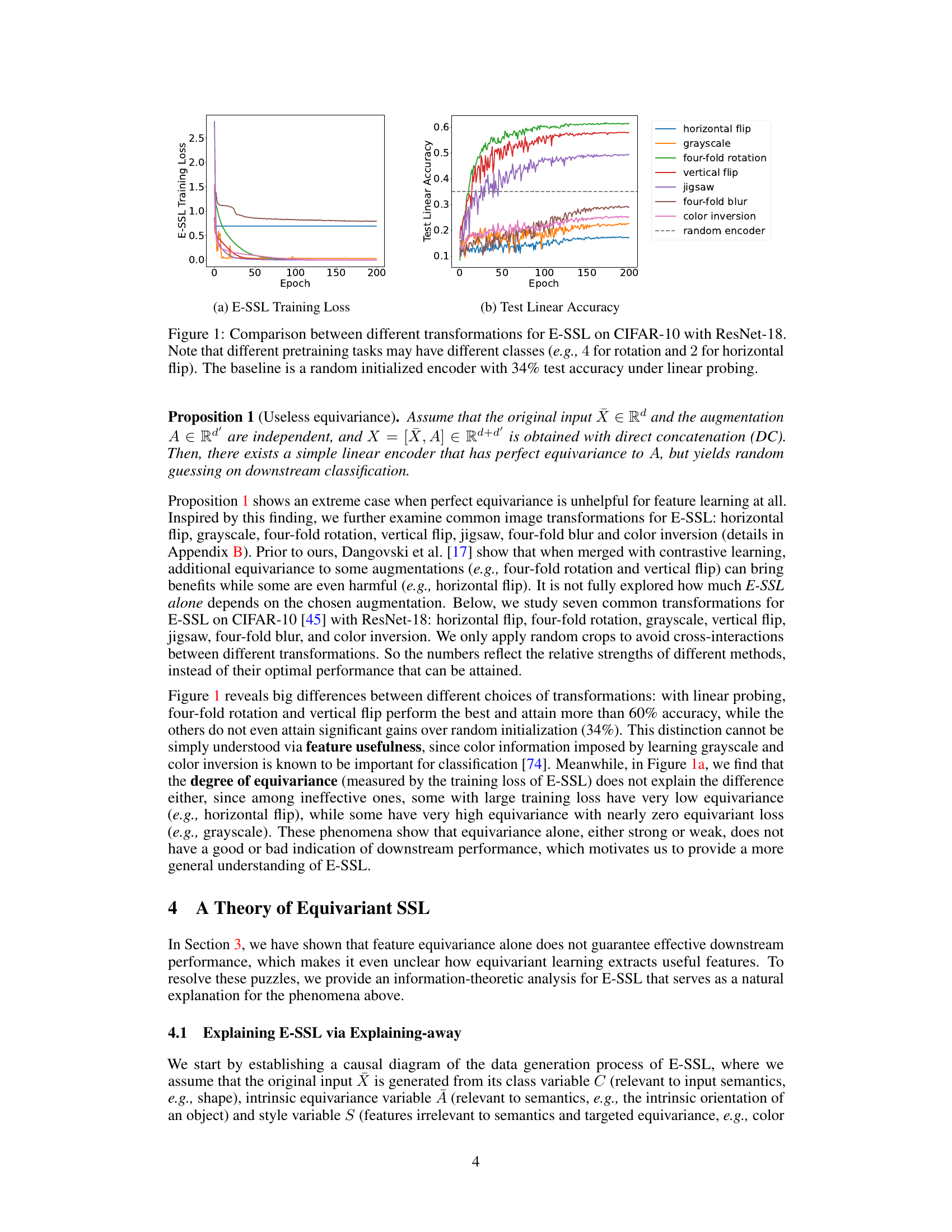
🔼 This figure compares the training loss and test linear accuracy of different transformations used in E-SSL on CIFAR-10 using ResNet-18. It shows the training loss curves for seven different transformations (horizontal flip, grayscale, four-fold rotation, vertical flip, jigsaw, four-fold blur, and color inversion) and a baseline of a randomly initialized encoder. The test linear accuracy curves for the same transformations and baseline are also plotted to show the performance of the learned representations on a downstream task (linear classification). The results indicate that the choice of transformation significantly impacts the performance of E-SSL.
read the caption
Figure 1: Comparison between different transformations for E-SSL on CIFAR-10 with ResNet-18. Note that different pretraining tasks may have different classes (e.g., 4 for rotation and 2 for horizontal flip). The baseline is a random initialized encoder with 34% test accuracy under linear probing.
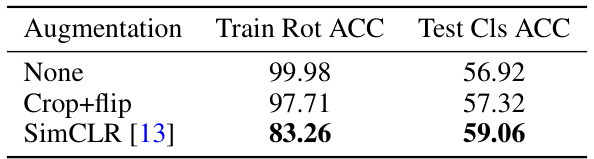
🔼 This table presents the results of an experiment comparing the performance of different augmentation strategies in a self-supervised learning setting. Specifically, it shows the training accuracy for rotation prediction and the test accuracy for linear classification after using different augmentations (None, Crop+flip, SimCLR) with ResNet-18 on the CIFAR-10 dataset. The goal is to determine how different levels of augmentation impact the performance of the model.
read the caption
Table 2: Training rotation prediction accuracy and test linear classification accuracy under different base augmentations (CIFAR-10, ResNet18).
In-depth insights#
Equivariance Synergy#
The concept of “Equivariance Synergy” in self-supervised learning (SSL) highlights the beneficial interplay between learning equivariant representations (sensitive to data augmentations) and achieving downstream task performance. Equivariance, by itself, doesn’t guarantee success; the key lies in how this augmentation-awareness interacts with class-relevant information. A crucial aspect is the “explaining-away effect,” where learning to predict the augmentation enhances the model’s ability to extract class-relevant features. This synergy is maximized when augmentations are lossy (not perfectly reversible), relevant to the classes, and free of shortcuts. The theoretical framework presented emphasizes an information-theoretic perspective, using mutual information to quantify this interplay. This perspective not only explains existing methods but also guides the design of more effective E-SSL approaches by focusing on maximizing this synergistic relationship between equivariance and class-relevant features.
E-SSL Information#
In the hypothetical section ‘E-SSL Information,’ a deep dive into the core concepts of Equivariant Self-Supervised Learning (E-SSL) is warranted. This would involve a nuanced exploration of information-theoretic perspectives, emphasizing the explaining-away effect and its role in the synergy between equivariant and classification tasks. A key aspect would be the quantification of the relationship between model equivariance and its impact on downstream performance, moving beyond a simple correlation to a causal understanding. Furthermore, this section should analyze practical implications by detailing the impact of different augmentation choices on downstream performance, focusing on the tension between obtaining high equivariance scores and maintaining information relevant to classification. Ultimately, a thorough examination should illuminate the principles guiding successful E-SSL design, such as the necessity of using lossy transformations that preserve class-relevant information while pruning shortcuts and exploring the advantages of fine-grained and multivariate equivariance.
E-SSL Design#
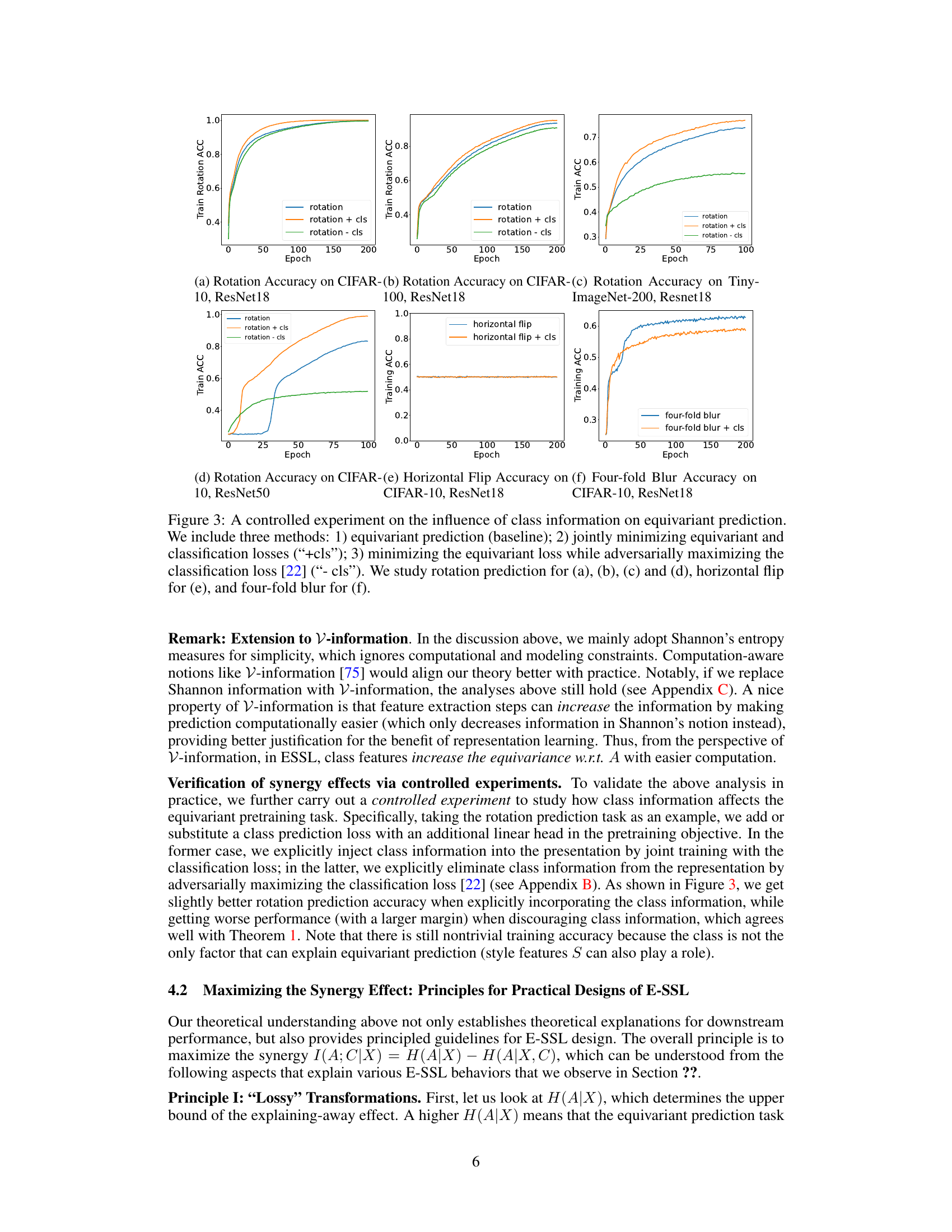
Equivariant self-supervised learning (E-SSL) design hinges on maximizing the synergy between equivariant prediction and class-relevant feature learning. Lossy transformations are crucial; they prevent perfect inference of the transformation from the augmented data, forcing the model to leverage class information for better prediction. This is exemplified by the contrast between effective transformations (rotation) and ineffective ones (grayscale). Class relevance is paramount; the chosen transformations should allow class information to improve equivariant prediction, highlighting the benefit of transformations with global effects (rotation) over local ones. Finally, shortcut pruning becomes important as it suppresses style-related features that could act as shortcuts, thus encouraging the model to learn deeper class-relevant features. These three principles provide a theoretical framework that explains the empirical success of many advanced E-SSL methods, such as the use of multiple transformations for multivariate equivariance and the incorporation of model equivariance for enhanced performance. The information-theoretic perspective emphasizes the importance of balancing task difficulty with the informative use of class information for effective E-SSL design.
Advanced E-SSL#
The section on “Advanced E-SSL” would delve into the evolution of equivariant self-supervised learning (E-SSL) beyond basic methods. It would likely explore techniques that enhance the synergy between class information and equivariant prediction, such as fine-grained equivariance, which increases the complexity and improves feature diversity. The discussion would also encompass multivariate equivariance, where multiple transformation variables are jointly predicted, leading to a stronger explaining-away effect and improved robustness. Finally, the critical role of model equivariance, using equivariant neural networks, would be examined, showing how alignment between model architecture and transformation properties boosts performance. This section would showcase how these advanced methods address limitations of simpler E-SSL approaches, illustrating a deeper understanding of equivariance’s role in learning useful, robust features for downstream tasks. Theoretical analysis and empirical results would likely support the claims of improved performance and robustness.
Future of E-SSL#
The future of equivariant self-supervised learning (E-SSL) is promising, with several key areas ripe for exploration. A deeper theoretical understanding of the explaining-away effect and its interplay with various data augmentations is crucial for developing more principled and effective E-SSL methods. Incorporating model equivariance into existing E-SSL frameworks can significantly boost performance, as demonstrated by the use of equivariant neural networks. Exploring fine-grained equivariance by predicting more detailed transformations will likely yield richer representations. Furthermore, combining E-SSL with invariant SSL (I-SSL) methods in a synergistic way, rather than solely relying on either approach, presents exciting possibilities. Finally, research into more complex, multivariate equivariance—jointly predicting multiple transformations—will likely lead to more robust and versatile E-SSL systems.
More visual insights#
More on figures
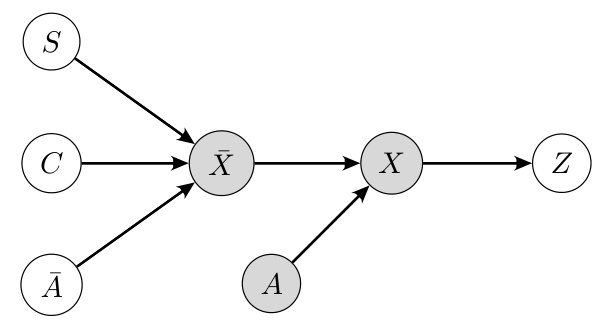
🔼 This figure shows a causal diagram representing the data generation process in equivariant self-supervised learning. The nodes represent variables, with shaded nodes representing observed variables and unshaded nodes representing latent variables. The arrows indicate causal relationships. The variables are: C (class), S (style), Ā (intrinsic equivariance), X (raw input), A (augmentation), X (augmented input), and Z (representation). The diagram illustrates how the class, style, and intrinsic equivariance influence the raw input, which is then augmented to produce the final input used to generate a representation. This helps illustrate the ’explaining away’ effect discussed in the paper, showing the relationships between class, augmentation, and representation.
read the caption
Figure 2: The causal diagram of equivariant self-supervised learning. The observed variables are in grey. C: class; S: style; A: intrinsic equivariance variable; X: raw input; A: augmentation; X: augmented input; Z: representation.

🔼 This figure compares the training loss and test accuracy of different data augmentation methods for equivariant self-supervised learning (E-SSL) on the CIFAR-10 dataset using a ResNet-18 model. It shows the training loss curves for various transformations like horizontal flip, grayscale, four-fold rotation, vertical flip, jigsaw, four-fold blur, and color inversion. The test accuracy, measured using linear probing, is also displayed for each transformation. A baseline using a randomly initialized encoder is included for comparison. The results highlight the significant performance differences obtained with different augmentation types, suggesting that simply achieving high equivariance isn’t sufficient to guarantee high downstream task performance. Some transformations result in very low accuracy, despite having a low training loss.
read the caption
Figure 1: Comparison between different transformations for E-SSL on CIFAR-10 with ResNet-18. Note that different pretraining tasks may have different classes (e.g., 4 for rotation and 2 for horizontal flip). The baseline is a random initialized encoder with 34% test accuracy under linear probing.
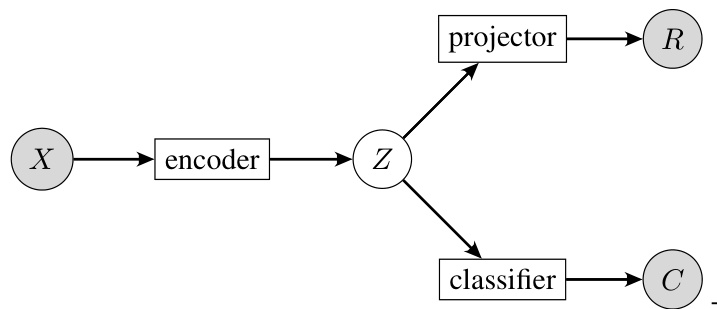
🔼 This figure shows the architecture used in the experiment to study how class information affects equivariant pretraining tasks. The input X is first encoded into a representation Z. This representation is then passed through two separate branches: one for rotation prediction (R), and one for class prediction (C). The gradient from the classifier to the encoder is detached for the rotation prediction task, unless explicitly specified. This setup allows researchers to isolate and analyze the impact of class information on the equivariance learning process.
read the caption
Figure 4: The model of this experiment. X: raw input; Z: representation; R: rotation prediction; C: class prediction. For rotation prediction, unless specified, the gradient flowing from the classifier to the encoder is detached.
More on tables
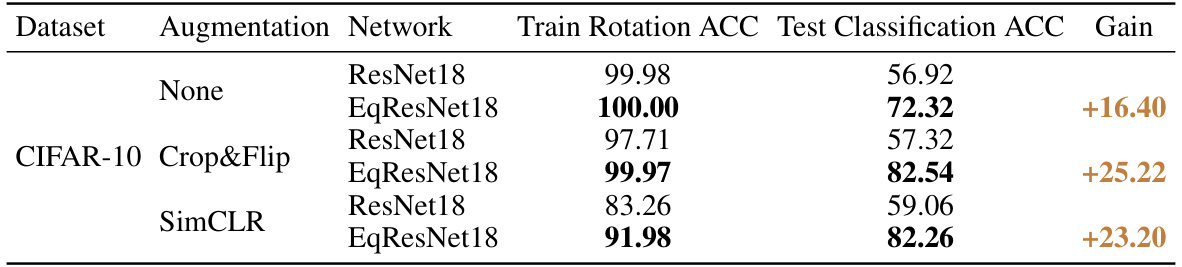
🔼 This table presents the results of experiments comparing the performance of ResNet18 and its equivariant counterpart (EqResNet18) on CIFAR-10 dataset using three different augmentation strategies: no augmentation, crop and flip, and SimCLR. For each augmentation strategy, the table displays the training accuracy of the rotation prediction task, the test accuracy achieved via linear probing for classification, and the gain in classification accuracy obtained by using the equivariant model over the non-equivariant model. The table showcases the benefits of using equivariant models, particularly under more aggressive augmentation schemes like SimCLR.
read the caption
Table 2: Training rotation prediction accuracy and test linear classification accuracy under different base augmentations (CIFAR-10, ResNet18).

🔼 This table compares the performance of two different loss functions for training an equivariant neural network on the CIFAR-10 dataset using a ResNet-18 architecture. The ‘CE loss’ row shows results using cross-entropy loss for predicting the rotation angle of augmented images. The ‘CARE loss’ row presents results when using the CARE (Contrastive Augmentation-Aware Rotation Equivariant) loss, which enforces strict equivariance. The table highlights that the CARE loss leads to improved performance in both the training rotation accuracy and the downstream classification accuracy after linear probing.
read the caption
Table 3: Comparison of augmentation-aware and truly equivariant methods (CIFAR-10, ResNet18).

🔼 This table presents a comparison of the training rotation prediction accuracy and test linear classification accuracy achieved using ResNet18 and an equivariant ResNet18 (EqResNet18) model on the CIFAR-10 dataset under different base augmentations. The augmentations include no augmentation, a combination of random cropping and flipping, and SimCLR augmentations. The table shows that the equivariant model consistently outperforms the standard ResNet18 model in terms of both training and test accuracy, demonstrating the benefits of incorporating equivariance into the model architecture.
read the caption
Table 2: Training rotation prediction accuracy and test linear classification accuracy under different base augmentations (CIFAR-10, ResNet18).

🔼 This table presents the results of an experiment comparing the performance of standard ResNet18 and equivariant ResNet18 models on the CIFAR-100 dataset. The models were pre-trained using rotation prediction, and their performance is evaluated using both the training rotation accuracy and the test classification accuracy after linear probing. The results are shown for three different augmentation strategies: no augmentation, crop and flip, and SimCLR augmentations. The ‘Gain’ column shows the improvement in test classification accuracy achieved by using the equivariant model compared to the standard model. This demonstrates the benefit of incorporating model equivariance for improving the quality of learned representations and the downstream classification performance.
read the caption
Table 4: Training rotation prediction accuracy and test linear classification accuracy under different base augmentations (CIFAR-100, ResNet18).
Full paper#