TL;DR#
Entropic-regularized optimal transport (OT) is essential for machine learning but existing methods like Sinkhorn are slow. Newton methods are faster but computationally expensive due to dense Hessian matrices. Sparsified Hessian-based methods improve speed but lack convergence guarantees and may encounter singularity issues.
This paper introduces the Safe and Sparse Newton method (SSNS) to overcome these challenges. SSNS uses a novel Hessian sparsification scheme with guaranteed positive definiteness, leading to a robust and efficient algorithm. The authors provide a thorough theoretical analysis, demonstrating global and quadratic local convergence, and offer a practical implementation without extensive hyperparameter tuning. Numerical experiments showcase SSNS’s effectiveness on large-scale OT problems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in optimal transport and machine learning due to its development of a novel, efficient algorithm (SSNS) for solving large-scale entropic-regularized optimal transport problems. The rigorous theoretical analysis and practical implementation make it highly relevant to current research trends and open avenues for further investigation in areas like deep learning and large-scale data analysis.
Visual Insights#

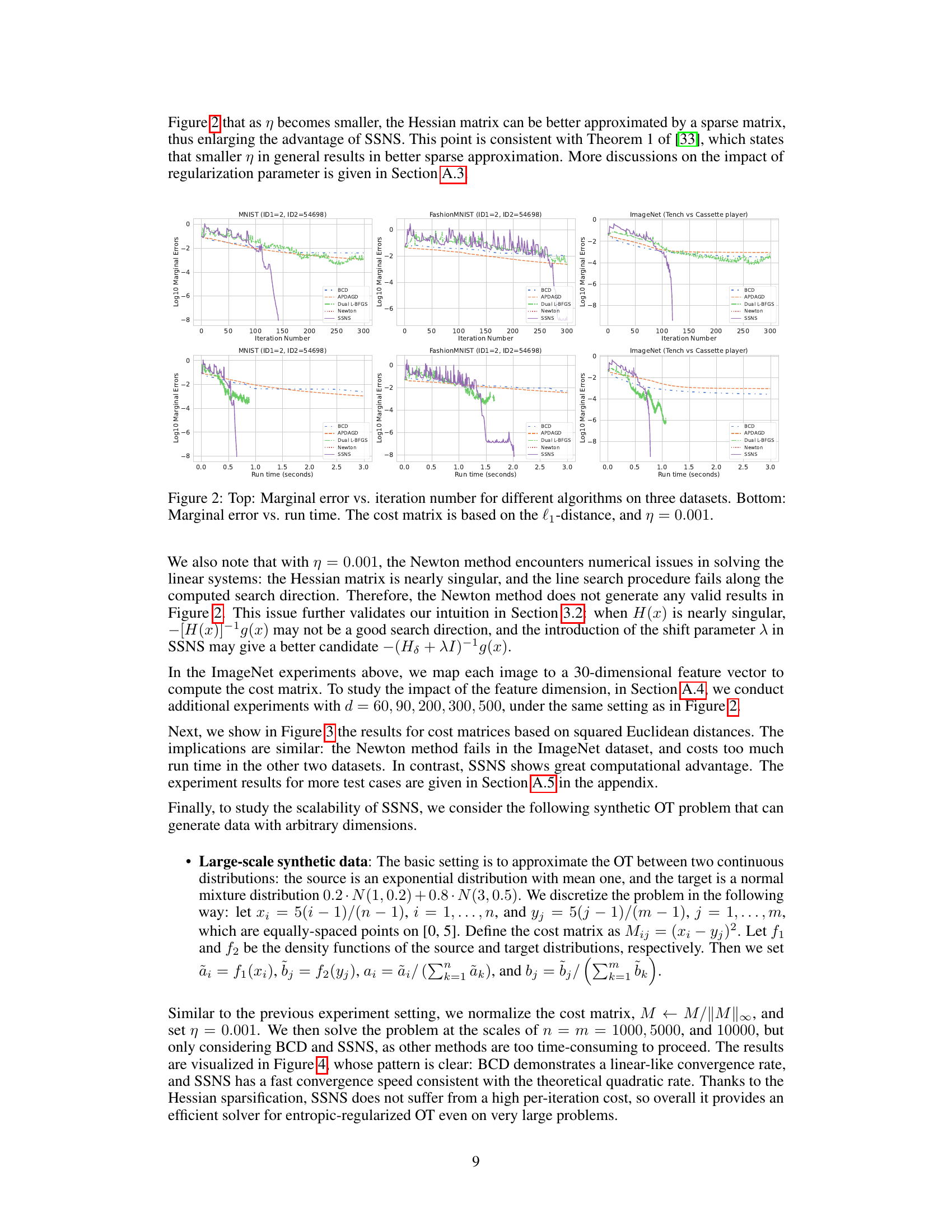
🔼 This figure compares the performance of five different algorithms (BCD, APDAGD, Dual L-BFGS, Newton, and SSNS) for solving entropic-regularized optimal transport problems on three benchmark datasets: MNIST, Fashion-MNIST, and ImageNet. The top row shows the convergence of the algorithms in terms of marginal error against the number of iterations. The bottom row shows the same convergence, but instead plots the marginal error against the runtime. The cost matrix is based on the l1-distance, and the regularization parameter is set to η = 0.01. The figure demonstrates that the second-order methods (Newton and SSNS) converge faster than first-order methods (BCD and APDAGD), and the SSNS algorithm is more computationally efficient than the Newton method due to its sparsification scheme.
read the caption
Figure 1: Top: Marginal error vs. iteration number for different algorithms on three datasets. Bottom: Marginal error vs. run time. The cost matrix is based on the l₁-distance, and η = 0.01.

🔼 This table compares the performance of BCD and SSNS algorithms under various regularization parameters (η) for the ImageNet experiment. It shows the runtime (in seconds) and the number of iterations required by each algorithm to reach the convergence tolerance (Etol = 10⁻⁸). The comparison is shown separately for cost matrices based on the l₁-distance and the squared Euclidean distance.
read the caption
Table 1: Performance comparison between BCD and SSNS under different regularization parameters for the ImageNet experiment in Section 5. The convergence tolerance is set to Etol = 10−8. Left: cost matrix based on the l₁-distance. Right: cost matrix based on the squared Euclidean distance.
In-depth insights#
Hessian Sparsification#
Hessian sparsification is a crucial technique for efficiently applying Newton-type methods to large-scale optimization problems, especially in optimal transport. The core idea is to reduce the computational complexity of handling the dense Hessian matrix by approximating it with a sparse matrix. This approximation is essential because inverting a dense Hessian has a cubic time complexity, which is prohibitive for high-dimensional problems. A successful sparsification scheme must carefully balance approximation accuracy with sparsity to ensure both computational efficiency and convergence guarantees. Different approaches exist for choosing which elements to retain in the sparse Hessian. Some methods are based on thresholding techniques, where small elements are discarded, others may involve selecting elements based on their impact on the overall structure of the matrix. Careful design is needed to ensure the resulting sparse Hessian remains positive definite to guarantee the convergence of the algorithm. The choice of sparsification scheme significantly impacts the algorithm’s practical performance, requiring careful consideration of trade-offs between computational cost and accuracy.
Safe Newton Method#
A safe Newton method, in the context of optimization, addresses the potential instability of standard Newton methods by incorporating mechanisms to ensure the method’s stability and convergence. The core idea is to modify the Hessian matrix or the search direction to avoid issues like singularity or ill-conditioning, which can prevent convergence or lead to inaccurate results. This modification may involve regularization, sparsification, or other techniques to improve the numerical properties of the Hessian. The ‘safe’ aspect implies that the method is designed to avoid failure or non-convergence, even when the problem is ill-conditioned or the initial guess is poor. A robust safe Newton method often involves sophisticated techniques to handle potential numerical issues while maintaining the desired quadratic convergence rate of Newton methods. This approach is particularly useful for large-scale or complex optimization problems where standard Newton methods may be prone to failure.
Convergence Analysis#
A rigorous convergence analysis is crucial for establishing the reliability and efficiency of any optimization algorithm. In the context of this research paper, a comprehensive convergence analysis would involve demonstrating both global convergence (guaranteeing convergence to an optimal solution from any starting point) and local convergence (analyzing the rate of convergence near the optimum). The analysis would need to account for the specific algorithm used, including its sparsification strategy and the method for determining step sizes, and would likely involve techniques from convex optimization theory. Theoretical bounds on the approximation error introduced by the sparsification scheme would be necessary to establish the overall convergence rate. The analysis should also address the potential for numerical instability arising from near-singularity of the Hessian matrix. Demonstrating quadratic local convergence, a hallmark of Newton-type methods, is a key goal. Finally, the analysis should provide insights into the algorithm’s practical performance and sensitivity to various hyperparameters. A comprehensive treatment of the convergence properties provides crucial evidence for the algorithm’s effectiveness and reliability.
OT Algorithm#
Optimal Transport (OT) algorithms are crucial for solving OT problems, which involve finding the optimal way to transport mass from one distribution to another. Many OT algorithms exist, each with strengths and weaknesses. Sinkhorn’s algorithm is popular due to its efficiency for entropic-regularized OT, but it’s a first-order method, meaning it can be slow to converge. Newton-type methods offer faster convergence but face challenges with computational cost due to dense Hessian matrices. Sparse Newton methods aim to address this by approximating the Hessian, allowing for faster iterations. However, safeguarding against singularity during matrix inversion is vital for robust performance. The choice of algorithm depends heavily on the problem size and desired accuracy. Advanced methods often incorporate techniques like Hessian sparsification and adaptive regularization to balance speed and stability. Future research may focus on developing even more efficient algorithms that can handle very large-scale problems.
Future Directions#
Future research could explore adaptive sparsification techniques that dynamically adjust sparsity based on the problem’s characteristics and the algorithm’s progress. Investigating the impact of different sparsification strategies on the overall efficiency and accuracy would be valuable. Additionally, theoretical analysis could be extended to provide tighter bounds on approximation errors and convergence rates, potentially leading to improved algorithms. Combining the strengths of second-order methods with other optimization techniques, like variance reduction methods, could yield even faster convergence for large-scale optimal transport problems. Exploring applications of the proposed safe and sparse Newton method to other areas of machine learning that involve large-scale optimization is also warranted. Finally, a more in-depth study on the impact of the regularization parameter and its interplay with the sparsification strategy would provide valuable insights into algorithm behavior.
More visual insights#
More on figures
🔼 This figure compares the performance of several optimization algorithms (BCD, APDAGD, Dual L-BFGS, Newton, and SSNS) on three benchmark datasets (MNIST, FashionMNIST, and ImageNet). The top row shows the marginal error over the number of iterations, while the bottom row presents the marginal error against run time. The cost matrix is calculated using the l₁-distance, and the regularization parameter η is set to 0.01. The results demonstrate that second-order methods (Newton and SSNS) achieve faster convergence than first-order and quasi-Newton methods.
read the caption
Figure 1: Top: Marginal error vs. iteration number for different algorithms on three datasets. Bottom: Marginal error vs. run time. The cost matrix is based on the l₁-distance, and η = 0.01.

🔼 This figure compares the performance of several optimal transport (OT) algorithms across three datasets: MNIST, FashionMNIST, and ImageNet. The top row shows the log10 of the marginal error plotted against the number of iterations for each algorithm. The bottom row shows the same log10 marginal error plotted against the runtime in seconds. The cost matrix used is based on the l1-distance, and the regularization parameter (η) is set to 0.01. Algorithms compared include BCD (Sinkhorn), APDAGD, Dual L-BFGS, Newton, and the proposed SSNS method. The results demonstrate that the second-order methods (Newton and SSNS) converge significantly faster in terms of iterations, but that SSNS has a runtime advantage over the standard Newton method due to its use of sparse matrices.
read the caption
Figure 1: Top: Marginal error vs. iteration number for different algorithms on three datasets. Bottom: Marginal error vs. run time. The cost matrix is based on the l₁-distance, and η = 0.01.

🔼 This figure compares the performance of five different algorithms for solving entropic-regularized optimal transport (OT) problems on three benchmark datasets: MNIST, Fashion-MNIST, and ImageNet. The top row shows the log10 of the marginal error plotted against the number of iterations for each algorithm. The bottom row shows the same log10 marginal error, but plotted against the run time in seconds. The cost matrix used is based on the l₁-distance, and the regularization parameter η is set to 0.01. The algorithms compared are BCD (Sinkhorn), APDAGD, dual L-BFGS, Newton, and the authors’ proposed SSNS algorithm. The figure demonstrates that SSNS converges significantly faster than first-order methods while offering competitive run time compared to the vanilla Newton method.
read the caption
Figure 1: Top: Marginal error vs. iteration number for different algorithms on three datasets. Bottom: Marginal error vs. run time. The cost matrix is based on the l₁-distance, and η = 0.01.

🔼 This figure compares the performance of five different algorithms (BCD, APDAGD, Dual L-BFGS, Newton, and SSNS) for solving entropic-regularized optimal transport problems on three datasets (MNIST, Fashion-MNIST, and ImageNet). The top row shows the logarithmic marginal error against the iteration number, while the bottom row displays the logarithmic marginal error against the runtime in seconds. The cost matrix is computed using the l₁-distance, and the regularization parameter η is set to 0.01. The results demonstrate that second-order methods (Newton and SSNS) converge much faster than first-order methods but that the SSNS method is superior in runtime performance due to its efficient sparsification techniques.
read the caption
Figure 1: Top: Marginal error vs. iteration number for different algorithms on three datasets. Bottom: Marginal error vs. run time. The cost matrix is based on the l₁-distance, and η = 0.01.
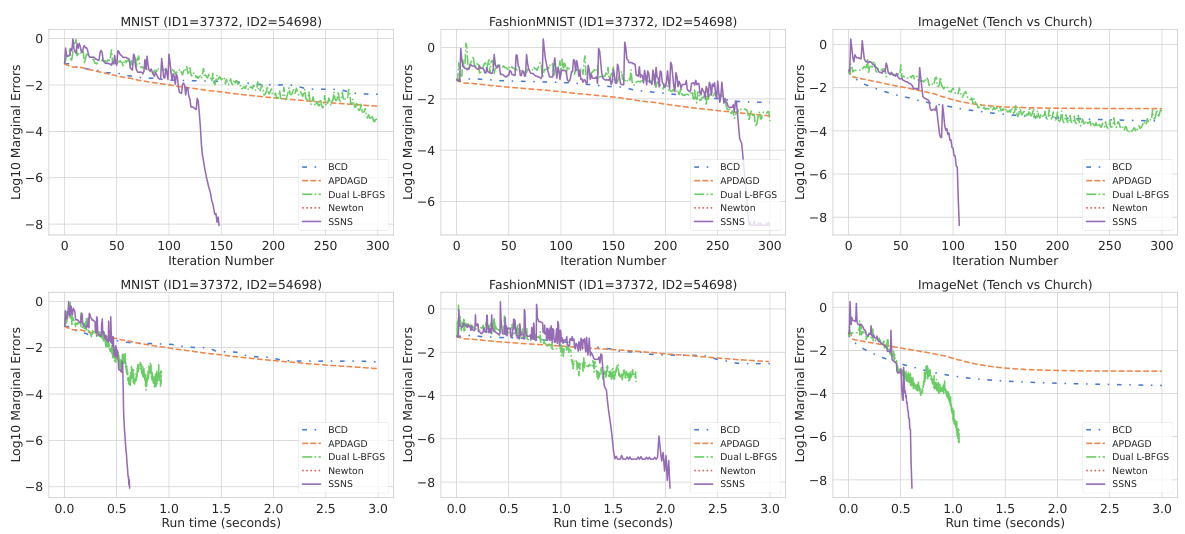
🔼 This figure compares the performance of several optimization algorithms (BCD, APDAGD, Dual L-BFGS, Newton, and SSNS) for solving entropic-regularized optimal transport problems. The top row shows the convergence behavior in terms of marginal error against the number of iterations, while the bottom row shows the run time performance. The cost matrix is based on the l1-distance, and the regularization parameter is set to η = 0.01. The datasets used are MNIST, FashionMNIST, and ImageNet.
read the caption
Figure 1: Top: Marginal error vs. iteration number for different algorithms on three datasets. Bottom: Marginal error vs. run time. The cost matrix is based on the l₁-distance, and η = 0.01.

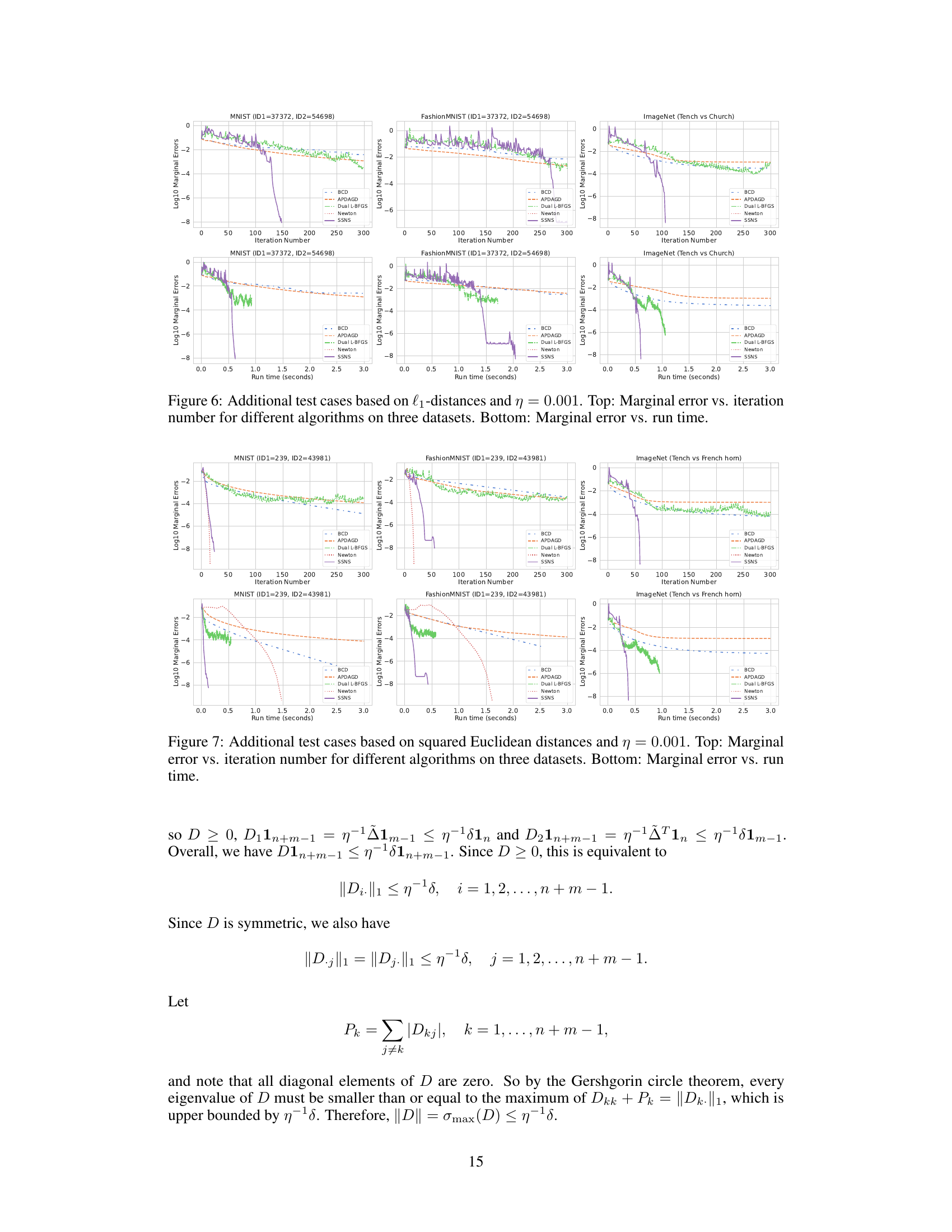
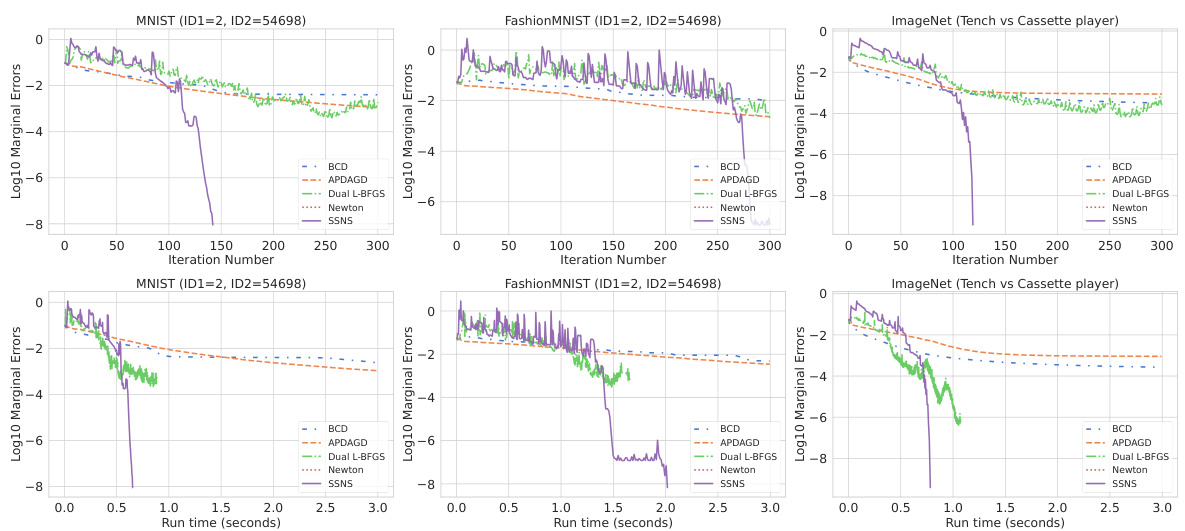
🔼 This figure compares the performance of five different algorithms (BCD, APDAGD, Dual L-BFGS, Newton, and SSNS) for solving entropic-regularized optimal transport problems on three datasets (MNIST, FashionMNIST, and ImageNet). The top row shows the marginal error plotted against the iteration number, while the bottom row shows the marginal error against the run time. The cost matrix is based on the l₁-distance, and the regularization parameter η is set to 0.001. The results demonstrate the superior performance of SSNS, especially in terms of run time.
read the caption
Figure 2: Top: Marginal error vs. iteration number for different algorithms on three datasets. Bottom: Marginal error vs. run time. The cost matrix is based on the l₁-distance, and η = 0.001.
Full paper#