↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Massive datasets are increasingly represented using graphs, but their size poses computational challenges. Existing graph coarsening techniques, which simplify graphs while preserving essential information, often struggle with speed and are limited to specific types of graphs. This significantly hinders analysis of large datasets.
This research introduces Universal Graph Coarsening (UGC), a new method that addresses these limitations. UGC leverages hashing for efficiency, achieving a linear time complexity making it much faster than existing methods. It also handles both homophilic and heterophilic graphs, a significant improvement over existing techniques. Experiments demonstrate UGC’s superior performance in terms of speed, accuracy in preserving graph properties, and overall effectiveness in downstream tasks, even at high coarsening ratios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large graphs because it introduces UGC, a novel framework that significantly accelerates graph coarsening while preserving essential graph properties. This addresses a major computational bottleneck in graph-based analyses, impacting various fields like social network analysis, bioinformatics, and natural language processing. Its versatility in handling both homophilic and heterophilic datasets opens new avenues for research and application.
Visual Insights#

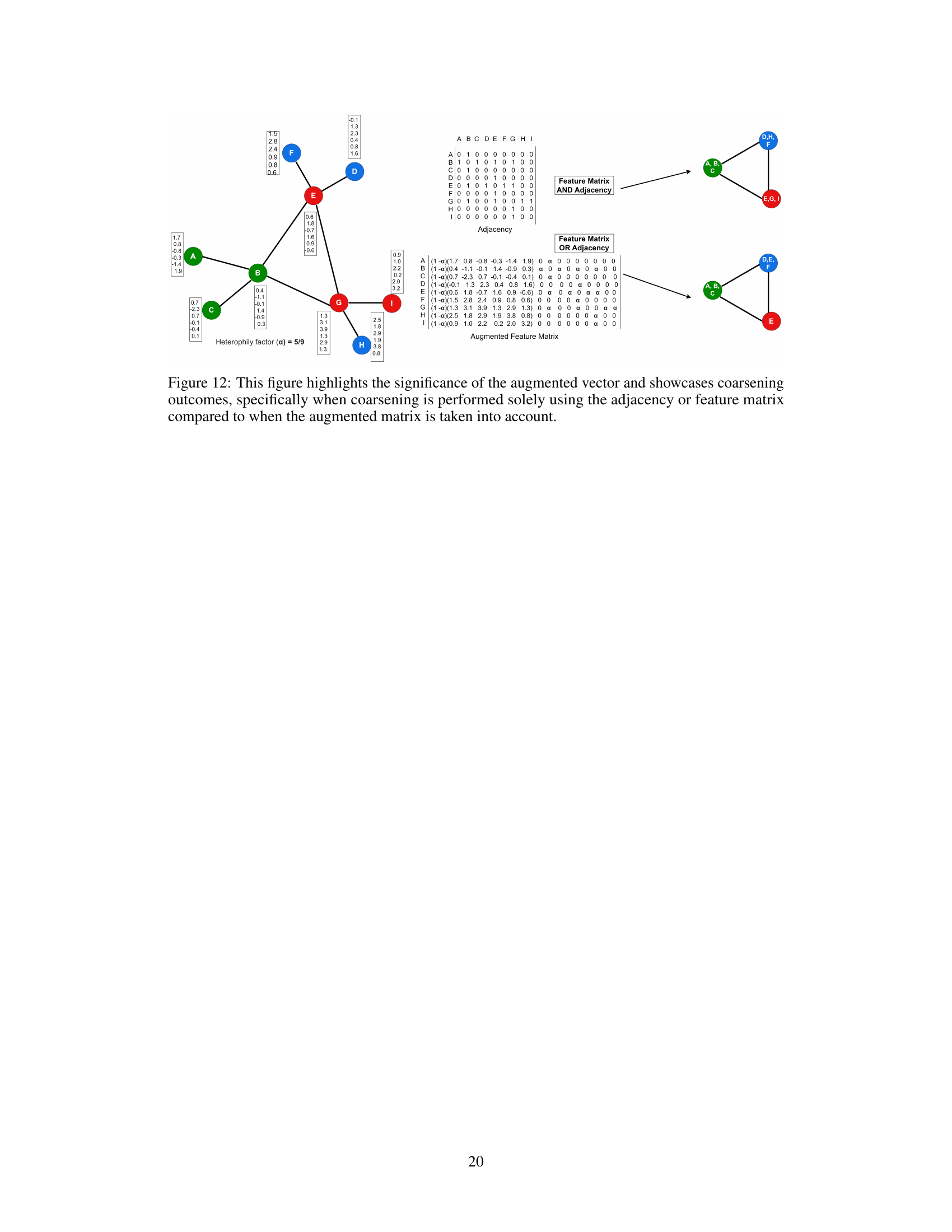
This figure illustrates the UGC framework, which consists of three main modules: 1) Generation of an augmented matrix by combining feature and adjacency matrices using the heterophily measure ‘a’. 2) Generation of a coarsening matrix ‘C’ using the augmented features and hashing. 3) Generation of the coarsened graph ‘Gc’ from ‘C’, which is then used in downstream tasks. The figure visually shows the flow of data and processes through these three modules.

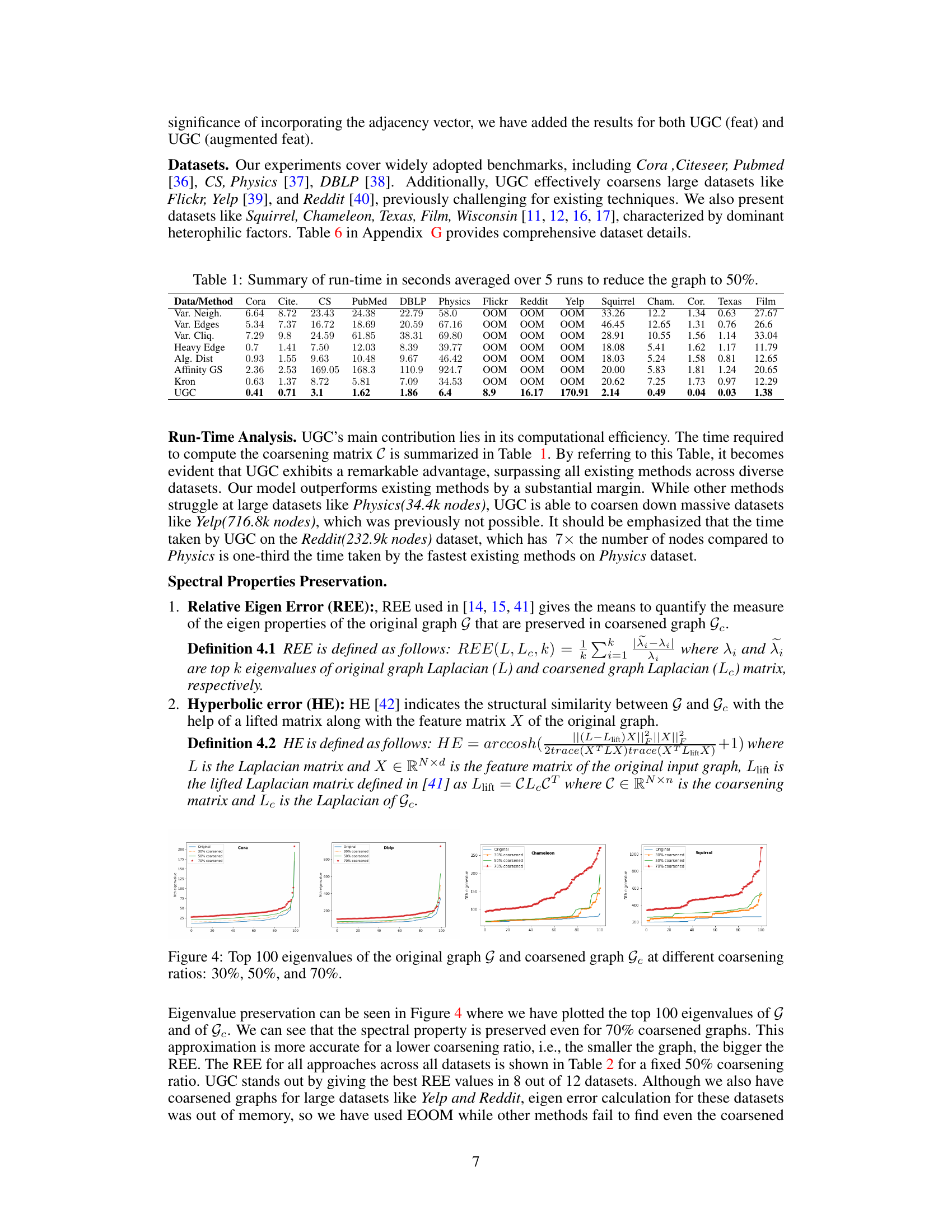
This table presents a comparison of the computational time taken by different graph coarsening methods to reduce the size of various graph datasets by 50%. The runtimes are averaged over five runs for each method and dataset. It highlights the significant speedup achieved by the proposed UGC method compared to existing techniques.
In-depth insights#
Universal GC#
Universal Graph Coarsening (UGC) presents a novel framework for efficiently downsampling large graphs while preserving crucial information. Its key strength lies in its universality, handling both homophilic and heterophilic datasets effectively, a significant improvement over existing methods. This is achieved by integrating node attributes and adjacency information, leveraging a heterophily factor to balance their influence. The method is also exceptionally fast, outperforming existing techniques by a factor of 4x to 15x, primarily due to its use of Locality Sensitive Hashing for efficient supernode identification. Furthermore, UGC demonstrates superior performance on downstream tasks, even with significant coarsening ratios (up to 70%), showcasing excellent preservation of spectral properties and reduced eigen-error. Overall, UGC offers a significant advancement for graph processing, offering both speed and accuracy in graph simplification. The linear time complexity is a significant advantage for scalability.
LSH-Based Hashing#
Locality Sensitive Hashing (LSH) offers a powerful technique for efficiently processing high-dimensional data. In the context of graph coarsening, LSH-based hashing leverages the ability of LSH to map similar data points to the same hash bucket. This is particularly useful for handling the complex feature vectors often associated with graph nodes. By using LSH to create a hash function, the algorithm can quickly determine which nodes share similar features. This dramatically reduces the time complexity of the coarsening process. The algorithm’s effectiveness hinges on the selection of an appropriate hash family and parameters to ensure that similar nodes are grouped together while dissimilar nodes are separated. However, a crucial consideration lies in balancing the trade-off between computational efficiency and the accuracy of the similarity preservation. An improperly configured LSH scheme might lead to significant information loss during the coarsening stage and adversely impact downstream tasks. Therefore, careful parameter tuning is essential to optimize the LSH-based hashing for a specific application and dataset.
Heterophilic Graphs#
Heterophilic graphs, unlike their homophilic counterparts, exhibit a fascinating characteristic: nodes tend to connect with dissimilar neighbors rather than similar ones. This characteristic poses significant challenges for traditional graph analysis techniques, many of which are built on the assumption of homophily (a preference for connections between similar nodes). Understanding heterophilic graphs is crucial because they represent many real-world networks such as those in social sciences, where connections might arise from conflict or contrasting viewpoints, or biological networks, exhibiting complex interdependencies. Developing methods robust to heterophily is an active area of research. The inherent complexity of heterophilic networks necessitates innovative approaches to tasks like community detection, link prediction, and node classification. Effective algorithms must go beyond simple similarity measures and incorporate structural information alongside node attributes to capture the subtleties of these relationships. Successfully modeling heterophilic graphs could significantly improve the accuracy and reliability of results in various applications.
Scalable GNN Training#
The section on “Scalable GNN Training” in the research paper explores the challenges of applying Graph Neural Networks (GNNs) to large-scale datasets. It highlights the computational limitations of training GNNs on massive graphs and proposes graph coarsening as a key solution. Graph coarsening reduces the size of the graph while attempting to preserve essential structural and spectral properties, making GNN training more efficient. The paper likely demonstrates the effectiveness of the proposed coarsening method by showing improved scalability and efficiency gains compared to existing methods. A key aspect to examine would be the trade-off between computational savings from coarsening and any potential loss in accuracy of GNN predictions on the original, uncoarsened graph. The authors likely present empirical evidence supporting the claim that their coarsening technique strikes a favorable balance, yielding both substantial speedups and minimal performance degradation. Finally, this section probably discusses the applicability of their approach across different GNN architectures and diverse datasets, showcasing its versatility and generalizability.
Future Work#
Future work could explore several promising directions. Extending UGC to dynamic graphs is crucial for real-world applications where relationships constantly evolve. Investigating different hashing techniques beyond LSH, perhaps incorporating learned embeddings, could improve accuracy and efficiency. A thorough analysis of the impact of the heterophily factor (α) on performance is warranted, potentially leading to adaptive methods that adjust α based on dataset characteristics. Finally, applying UGC to other graph-based tasks such as link prediction and community detection, and evaluating its performance against state-of-the-art methods, would further demonstrate its versatility and potential.
More visual insights#
More on figures
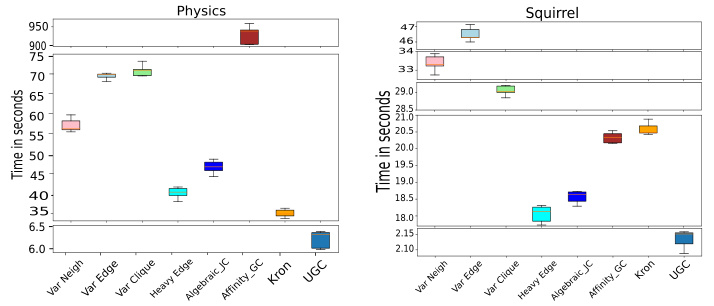
This figure presents a comparison of the computational time taken by different graph coarsening methods across two datasets: Physics and Squirrel. The methods are compared based on the time taken to execute ten iterations of the coarsening process. Universal Graph Coarsening (UGC) is shown to be significantly faster than other methods, achieving a speedup of approximately 6 times for the Physics dataset and 9 times for the Squirrel dataset.

This figure is a simple illustration of the graph coarsening process. Part (a) shows the coarsening matrix, which maps nodes from the original graph (b) to super-nodes in the coarsened graph (b). Nodes with similar features are grouped together into super-nodes, reducing the overall size and complexity of the graph while preserving important structural relationships.

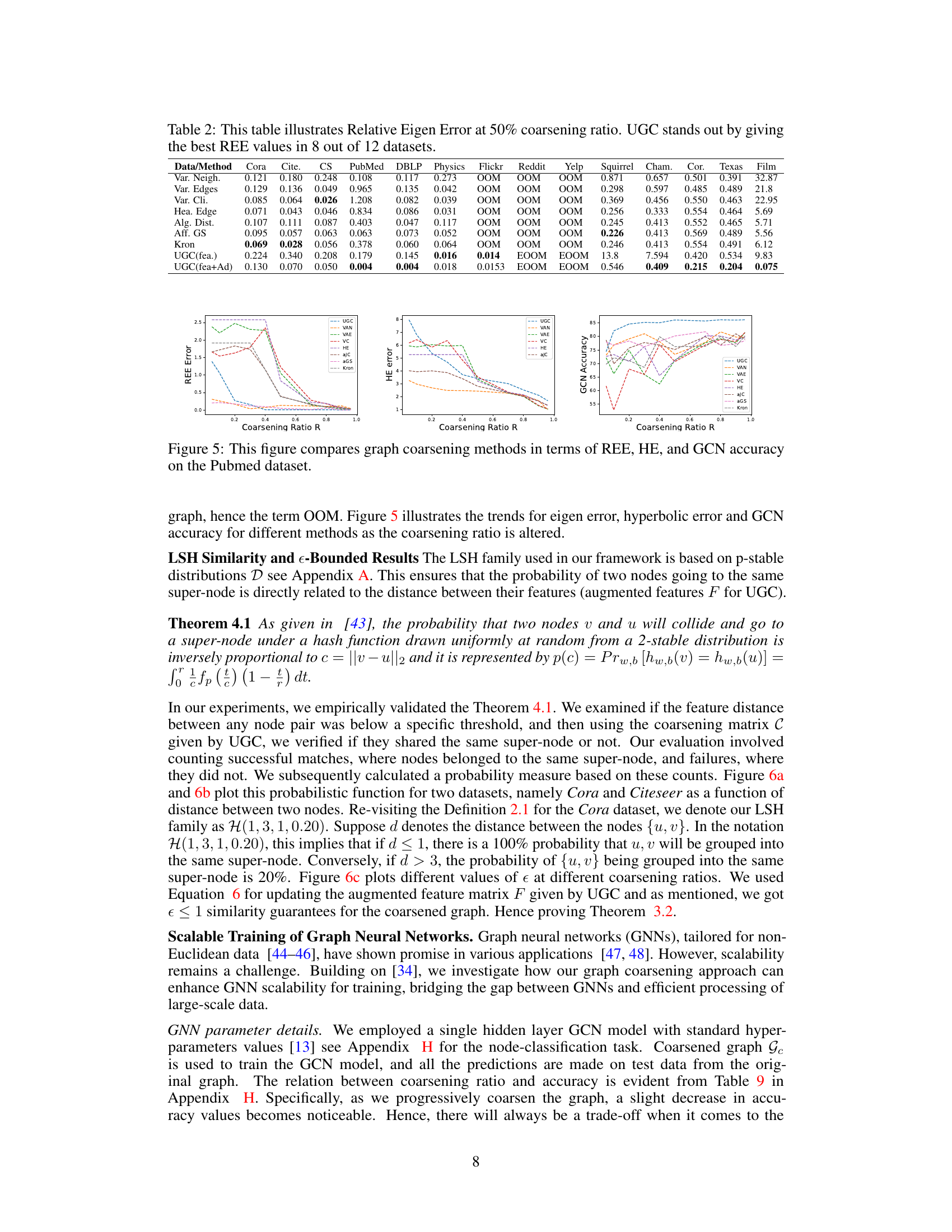
This figure shows the top 100 eigenvalues of the original graph and its coarsened versions at different coarsening ratios (30%, 50%, and 70%). It visually demonstrates the preservation of spectral properties (eigenvalues) by the UGC method, even with significant graph reduction. The similarity in eigenvalue distributions between the original and coarsened graphs highlights the effectiveness of UGC in maintaining crucial structural information during the coarsening process.

This figure displays the top 100 eigenvalues of both the original graph (G) and its coarsened version (Gc) at three different coarsening ratios (30%, 50%, and 70%). It visually demonstrates the effectiveness of the Universal Graph Coarsening (UGC) method in preserving the spectral properties of the graph even after significant reduction in size. The closeness of the eigenvalues between the original and coarsened graphs highlights the quality of the coarsening process and its ability to maintain crucial structural information.
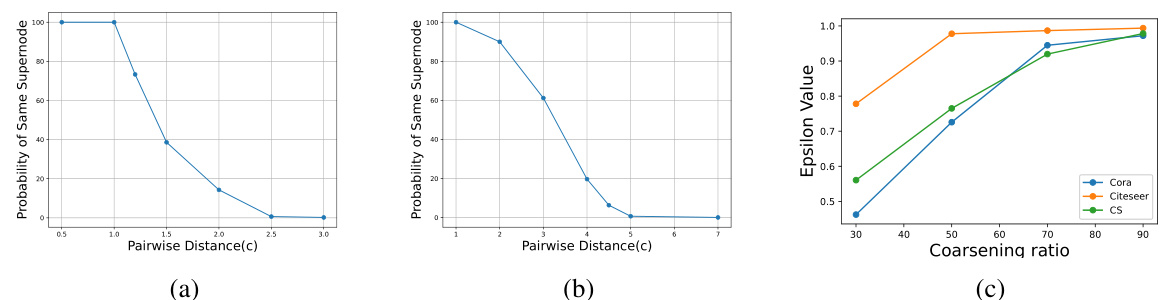
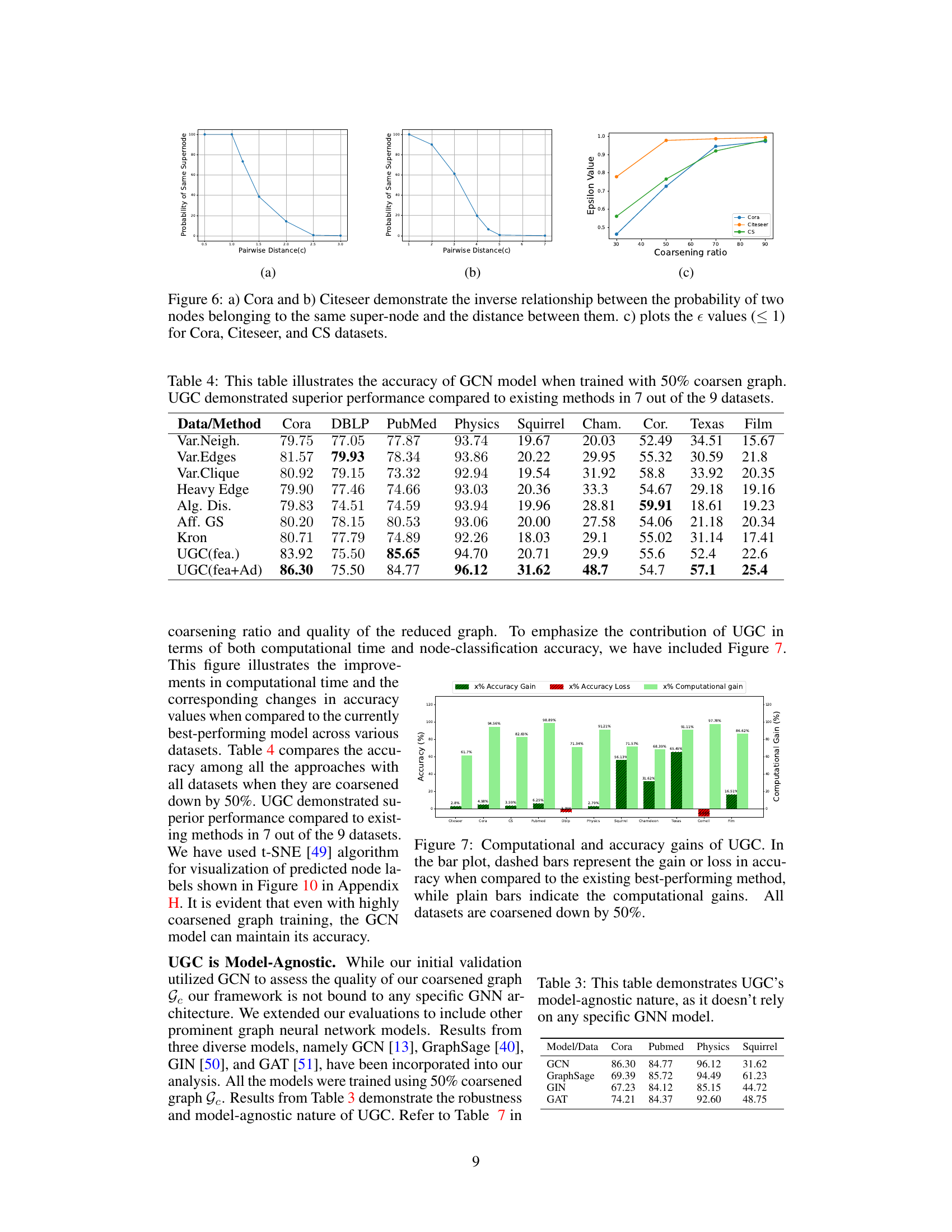
This figure shows the results of an experiment that validates the theoretical results regarding the LSH scheme. Specifically, it demonstrates the inverse relationship between the probability of two nodes being assigned to the same supernode and the distance between their features. The left and middle subfigures (a and b) show this relationship for Cora and Citeseer datasets, respectively. The right subfigure (c) shows how epsilon values (a measure of similarity between the original and coarsened graphs) change with different coarsening ratios for Cora, Citeseer, and CS datasets. The results indicate that LSH effectively groups similar nodes in the same supernode, as expected.
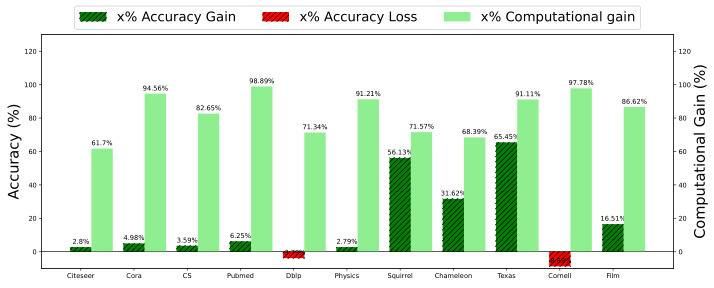
This figure compares the computational time and accuracy improvement achieved by UGC against existing state-of-the-art graph coarsening methods. The left bars show the speedup (computational gain) obtained by UGC when compared to the fastest existing methods. The right bars show the improvement (or loss) in accuracy after applying graph coarsening using UGC compared to the method with highest accuracy among existing methods. The results indicate that UGC is significantly faster and generally achieves comparable or better accuracy than other methods, even with a 50% coarsening ratio. This highlights the efficiency and effectiveness of UGC for downstream tasks.

The figure shows a bar chart comparing the computational time taken by different graph coarsening methods (Var Neigh, Var Edge, Var Clique, Heavy Edge, Algebraic JC, Affinity_GC, Kron, and UGC) to coarsen two datasets: Physics and Squirrel. The y-axis represents the time in seconds, and the x-axis shows the different methods. The chart demonstrates that UGC significantly outperforms all other methods in terms of speed, achieving a 6x speedup on the Physics dataset and a 9x speedup on the Squirrel dataset.

This figure visualizes the predicted nodes by a Graph Convolutional Network (GCN) model trained on coarsened versions of the Physics dataset. It showcases the impact of graph coarsening (at 30%, 50%, and 70% reduction) on the GCN’s ability to correctly classify nodes. By comparing the visualization of the original graph with the coarsened ones, one can assess how well the coarsening process preserves the essential structural information needed for effective GCN training and prediction.

The figure compares the computational time of several graph coarsening methods, including the proposed UGC method, across two datasets (Physics and Squirrel). The x-axis represents the graph coarsening method, and the y-axis represents the computation time in seconds. The results show that UGC significantly outperforms existing state-of-the-art methods in terms of speed, achieving 6x and 9x speedups on the Physics and Squirrel datasets respectively.

The figure compares the computational time taken by various graph coarsening methods to process graphs. It shows that Universal Graph Coarsening (UGC) is significantly faster than other methods, achieving speedups of 6x and 9x on the Physics and Squirrel datasets respectively, when running over ten iterations.
More on tables

This table presents the node classification accuracy achieved by different graph coarsening methods when training a Graph Convolutional Network (GCN) on a 50% coarsened graph. The methods compared include various established techniques and the proposed Universal Graph Coarsening (UGC) approach, both with and without adjacency information. The table highlights the superior performance of UGC, especially when incorporating adjacency information, across most datasets.
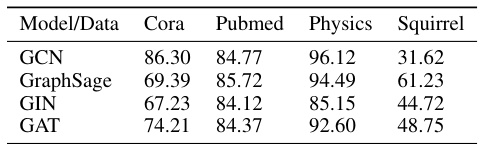
This table presents the node classification accuracy achieved by different Graph Neural Network (GNN) models trained on graphs coarsened to 50% using various methods. It compares the performance of Universal Graph Coarsening (UGC) against other graph coarsening techniques, highlighting UGC’s superior accuracy in most cases.
This table presents a comparison of the computational time taken by different graph coarsening methods to reduce the size of various benchmark datasets by 50%. The datasets used represent a mix of sizes and characteristics, allowing for a comprehensive assessment of each method’s efficiency in different contexts. The time reported is averaged over five runs for each method and dataset to provide a reliable estimate and reduce the impact of variance.

This table presents a comparison of the computation time required by different graph coarsening methods to reduce the size of various graphs by 50%. The methods compared include: Variable Neighborhood, Variable Edges, Variable Clique, Heavy Edge, Algebraic Distance, Affinity, Kronecker product, and the proposed UGC method. The datasets used are diverse and include both small and large graphs, showcasing the scalability of UGC. The results demonstrate UGC’s significant speed advantage over existing methods.

This table presents a comparison of the computation time taken by different graph coarsening methods to reduce the size of various benchmark graph datasets by 50%. The datasets include PubMed, DBLP, Physics, Flickr, Reddit, Yelp, Squirrel, Chameleon, Cora, Texas, Film, and Citeseer, showcasing the performance differences across diverse graph sizes and characteristics. The table highlights the significant speed advantage of the proposed UGC method compared to existing techniques.

This table compares the node classification accuracy achieved by four different Graph Neural Network (GNN) models (GCN, GraphSage, GIN, and GAT) when trained on graph datasets that have been coarsened to 50% of their original size using the Universal Graph Coarsening (UGC) method. The table shows that the performance of the GNN models can still be quite good even when trained on a much smaller graph, and that UGC is effective at preserving important information when coarsening graphs.
This table presents the accuracy of Graph Convolutional Networks (GCNs) for node classification after applying Universal Graph Coarsening (UGC) at different coarsening ratios (30%, 50%, and 70%). The accuracy is measured across four benchmark datasets: Cora, DBLP, Pubmed, and Physics. The table allows comparison of GCN performance on coarsened graphs against the original graphs.
Full paper#