↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large transformer models often suffer from outlier features (OFs) – neurons with unusually high activation magnitudes. These OFs hinder model quantization, a crucial technique for making models smaller and faster. Prior work provided limited understanding of why OFs appear and how to minimize them effectively.
This paper introduces a novel transformer block, the “Outlier Protected” (OP) block, that removes normalization layers to mitigate OFs. Furthermore, it highlights the benefit of using non-diagonal preconditioning optimizers, such as SOAP. The results show that combining the OP block and SOAP leads to significant OF reduction and improved int8 quantization performance even at larger scales (7B parameters), showcasing efficient and effective solutions to a major challenge in transformer training.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning and model compression. It addresses the problem of outlier features, which significantly hinder the efficiency and accuracy of quantized transformer models. The proposed solutions directly impact the performance and scalability of large-scale transformer training, contributing to faster convergence and improved model deployment. This work opens exciting new avenues for research into model optimization techniques and low-precision training methodologies.
Visual Insights#
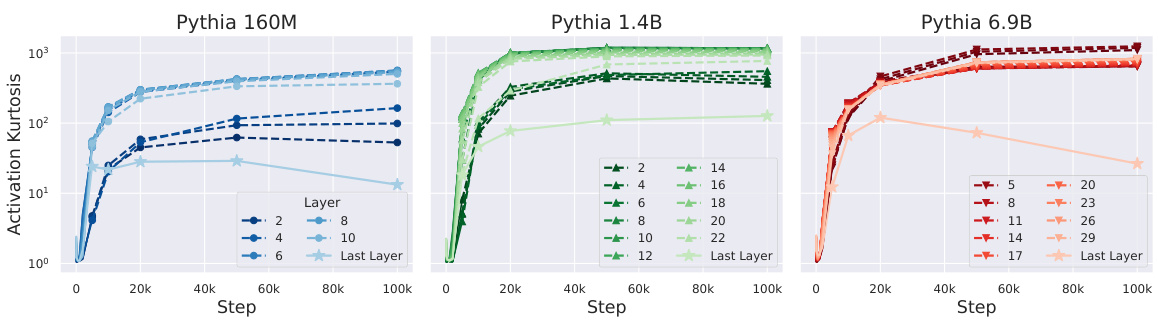
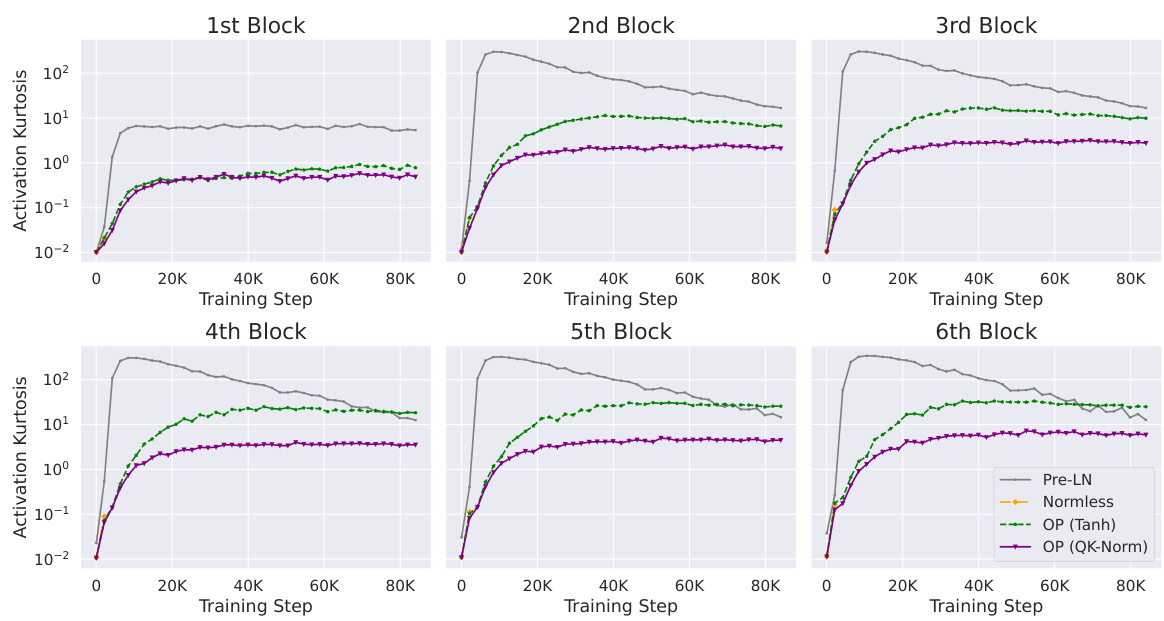
This figure shows the appearance of outlier features in three different sizes of Pythia transformer models during training. The outlier features are measured using the kurtosis metric defined in the paper. The figure shows that outlier features emerge during the training process and their emergence is influenced by various design choices.
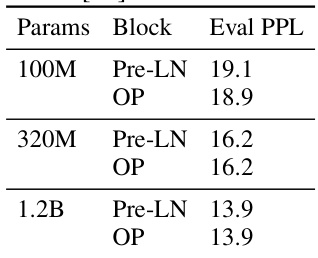
This table demonstrates the performance of the Outlier Protected (OP) block compared to the Pre-LN block across three different model sizes (100M, 320M, and 1.2B parameters). The evaluation metric used is perplexity (PPL) on the Languini Books dataset. The results show that the OP block achieves comparable perplexity to the Pre-LN block across all model sizes, indicating that the OP block can effectively minimize outlier features without compromising performance. The model sizes are measured by the number of parameters.
In-depth insights#
Outlier Feature Effects#
Outlier features (OFs), neurons with activation magnitudes significantly exceeding the average, pose substantial challenges in transformer training. OFs hinder quantization, leading to increased errors in low-precision models and impacting efficiency. This paper investigates OF emergence, exploring various architectural and optimization choices to minimize their effects. Normalization layers, while beneficial for training, are implicated in OFE. The study introduces a novel unnormalized transformer block and highlights a previously unknown benefit of non-diagonal preconditioners. These methods significantly reduce OFs without sacrificing convergence speed, demonstrating considerable improvements in quantization. The research also explores the link between OFs and signal propagation, suggesting that poor signal propagation leads to increased OFs. Furthermore, the impact of optimization choices, specifically learning rates and adaptive preconditioning, on OFE is analyzed, revealing strategies to mitigate OFs while maintaining efficient training.
OP Block Design#
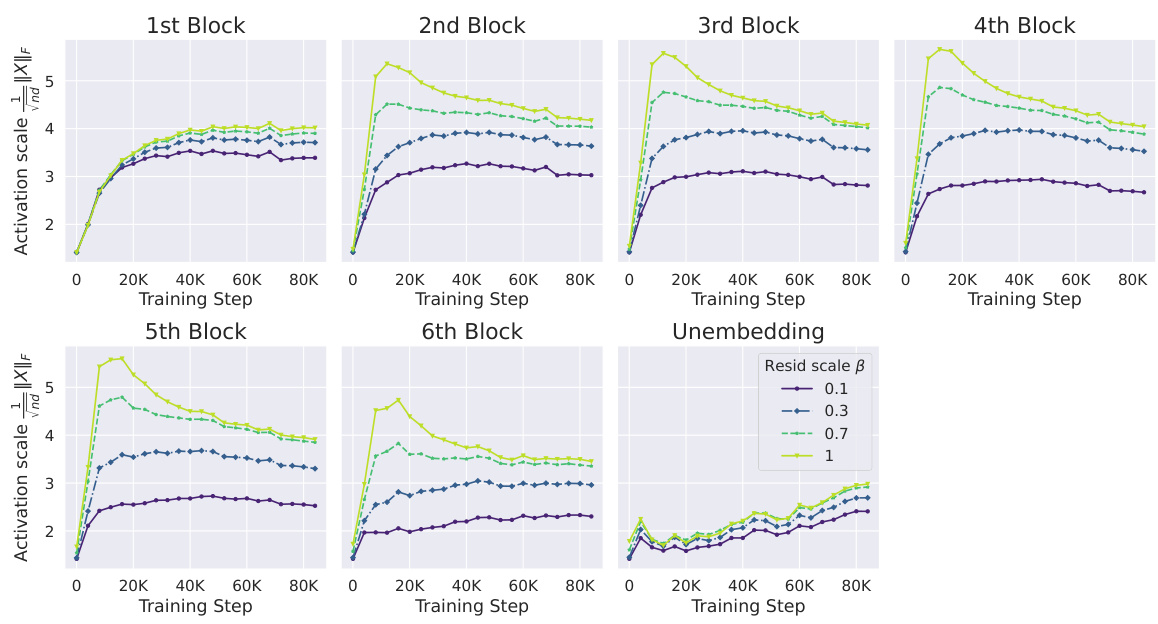
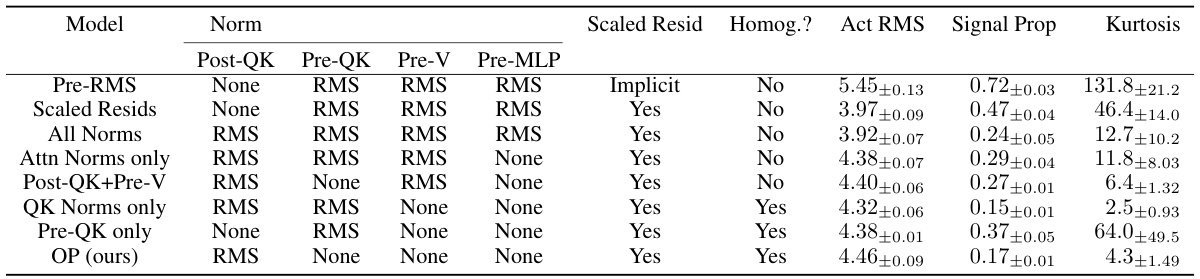
The Outlier Protected (OP) block is a novel transformer block design that directly addresses the issue of outlier features (OFs) in transformer models. Its core innovation is the removal of normalization layers, which previous research has implicated in the emergence of OFs. To compensate for the loss of normalization’s benefits (such as improved signal propagation and training stability), the OP block incorporates several key mechanisms: downweighted residual branches to maintain signal propagation; an entropy regulation mechanism (such as QK-Norm) to prevent entropy collapse, a common training instability in transformers; and optional input scaling to ensure that the nonlinearities receive inputs of the order of 1, improving the model’s numerical stability. This multi-pronged approach allows the OP block to effectively minimize OFs without compromising convergence speed or training stability, ultimately leading to models that are more amenable to quantization and efficient low-precision training.
Signal Propagation#
The concept of signal propagation in the context of neural networks, specifically transformers, is explored. The authors investigate its link to outlier features (OFs), neurons with unusually high activation magnitudes. Signal propagation studies how information flows through network layers, analyzing the input-wise Gram matrix (XXT). Poor signal propagation, nearing rank collapse where all inputs appear similar to deeper layers, is associated with OFs. The authors suggest that architectural choices impacting signal propagation directly influence the occurrence of OFs. Removing normalization layers, a key contributor to poor signal propagation, is proposed as a method to minimize OFs. Further, they identify that interventions to enhance signal propagation also effectively reduce OFEs. A key finding is the connection between poor signal propagation and increased activation kurtosis, a measure of OFs. The authors use this insight to develop the ‘Outlier Protected’ block, mitigating OFs without compromising training stability or convergence speed.
Optimizer Effects#
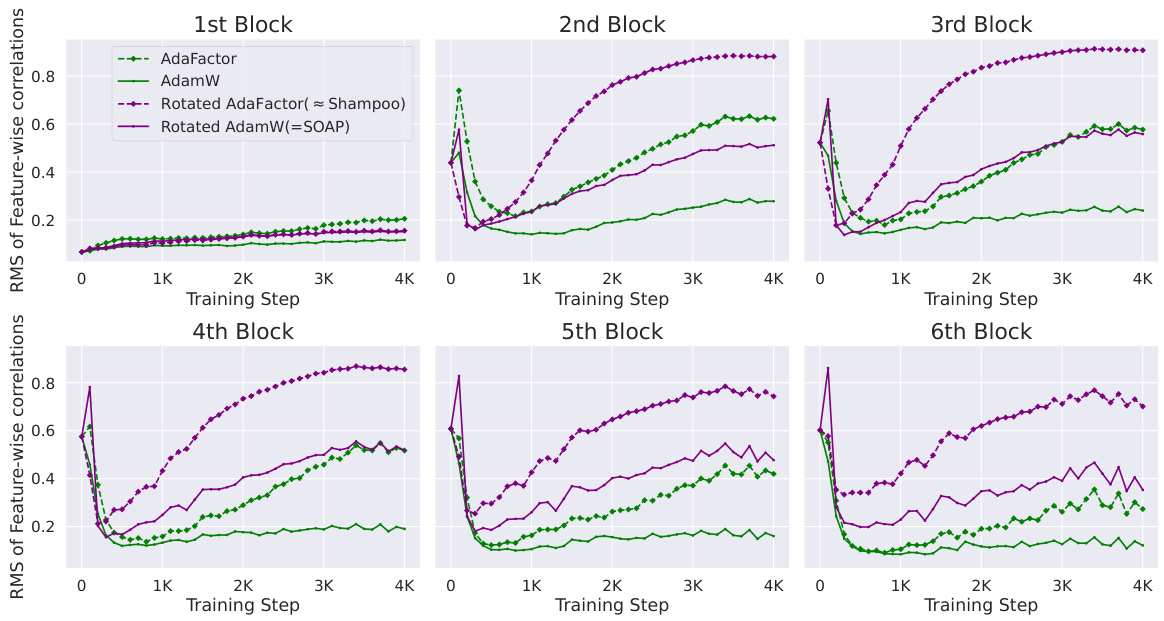
The research explores how optimizer choices significantly impact the emergence of outlier features (OFs) during transformer training. AdamW and AdaFactor, being adaptive diagonal preconditioners, exhibit a strong correlation between large adaptive learning rates and OF occurrence; smaller learning rates mitigate this. Conversely, non-diagonal preconditioners like Shampoo and SOAP, by rotating the parameter space before applying a diagonal optimization method, significantly minimize OFs, even with OF-prone architectures like Pre-Norm, demonstrating the importance of non-diagonal preconditioning. The study underscores the intricate interplay between optimizer characteristics and the occurrence of OFs, highlighting the potential benefits of sophisticated optimization techniques in improving the efficiency and robustness of large language model training.
Quantization Gains#
The research paper explores quantization, a technique to reduce the numerical precision of model parameters and activations. Significant quantization gains are reported, achieving a 14.87 int8 weight-and-activation perplexity (from 14.71 in standard precision) when combining an Outlier Protected (OP) block and a non-diagonal preconditioner (SOAP). This represents a substantial improvement over the 63.4 int8 perplexity (from 16.00) obtained with a default, outlier-prone combination of a Pre-Norm model and Adam. These gains are attributed to the mitigation of outlier features (OFs), which hinder quantization. The study highlights that architectural and optimization choices influence OFs, emphasizing that removing normalization layers and employing non-diagonal preconditioners significantly reduces OFs and leads to improved quantization performance. The Outlier Protected block, a novel unnormalized transformer block, plays a crucial role in achieving these benefits. Ultimately, the paper demonstrates that a thoughtful approach to minimizing outlier features is vital for successful low-precision model training and deployment. Further research is needed to fully understand and predict the emergence of outlier features in transformer training to enable further quantization improvement.
More visual insights#
More on figures

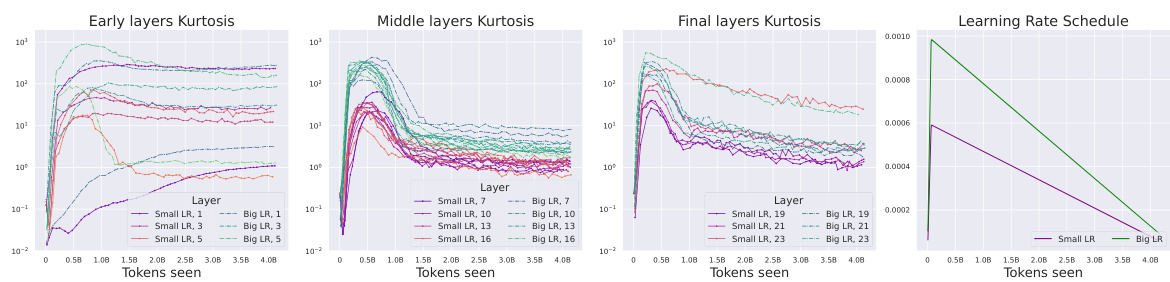
The figure shows the outlier features in three different sizes of Pythia transformers during training. The y-axis represents the kurtosis of neuron activation RMS, and the x-axis represents the training steps. Each plot shows how the kurtosis changes over training steps for different layers in the model. The outlier features are significant in these models and increase during training, especially in early layers. This paper investigates how architectural and optimization choices influence these outlier features and how to minimize them.

This figure shows the architecture of the Outlier Protected (OP) Transformer block, a novel unnormalised transformer block proposed in the paper. The OP block replaces the standard Pre-Norm block by removing the normalisation layers. Key improvements include downweighting residual branches to recover training benefits, adding an entropy regulation mechanism (like QK-Norm) to prevent entropy collapse and optionally scaling inputs before the MLP nonlinearity. The authors argue that this design minimizes outlier features.

The figure compares the activation kurtosis across layers between the Outlier Protected (OP) block and the standard Pre-LN block in a 1.2B parameter transformer. The OP block consistently shows lower kurtosis (up to 4 orders of magnitude) compared to the Pre-LN block, especially in the early layers. This reduction in kurtosis is significant because it indicates that the OP block effectively mitigates the Outlier Features (OFs) phenomenon, which is known to hinder model quantization. The figure supports the paper’s claim that the OP block improves model performance by mitigating OFE without compromising convergence speed.
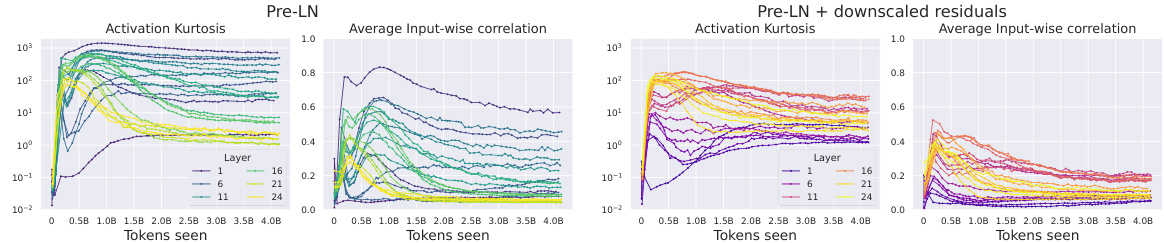
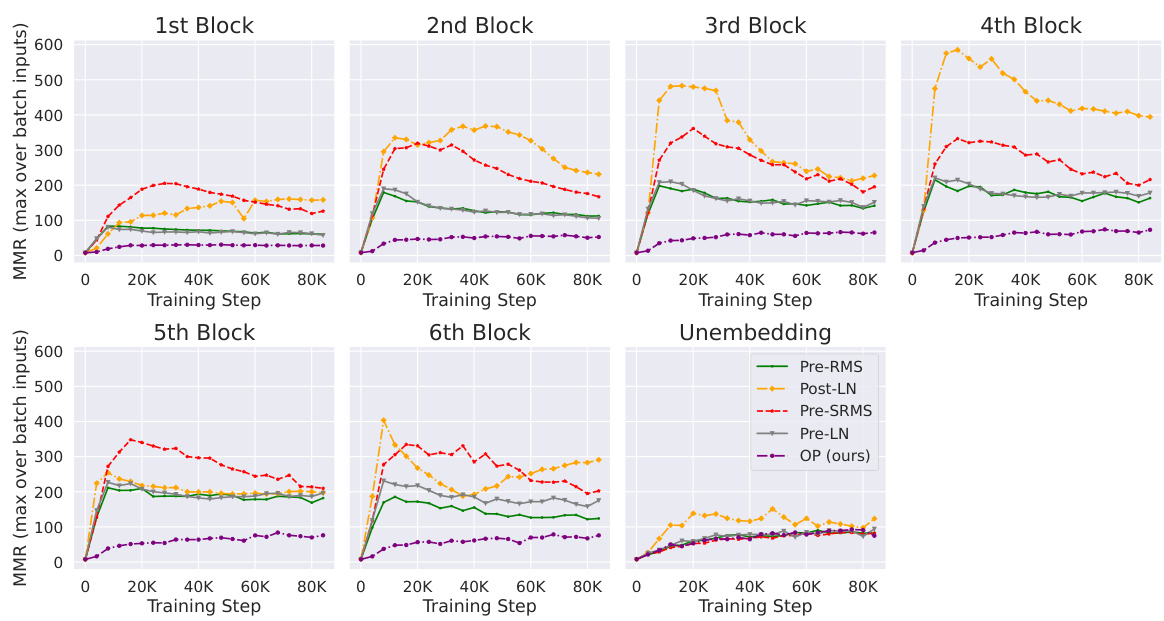
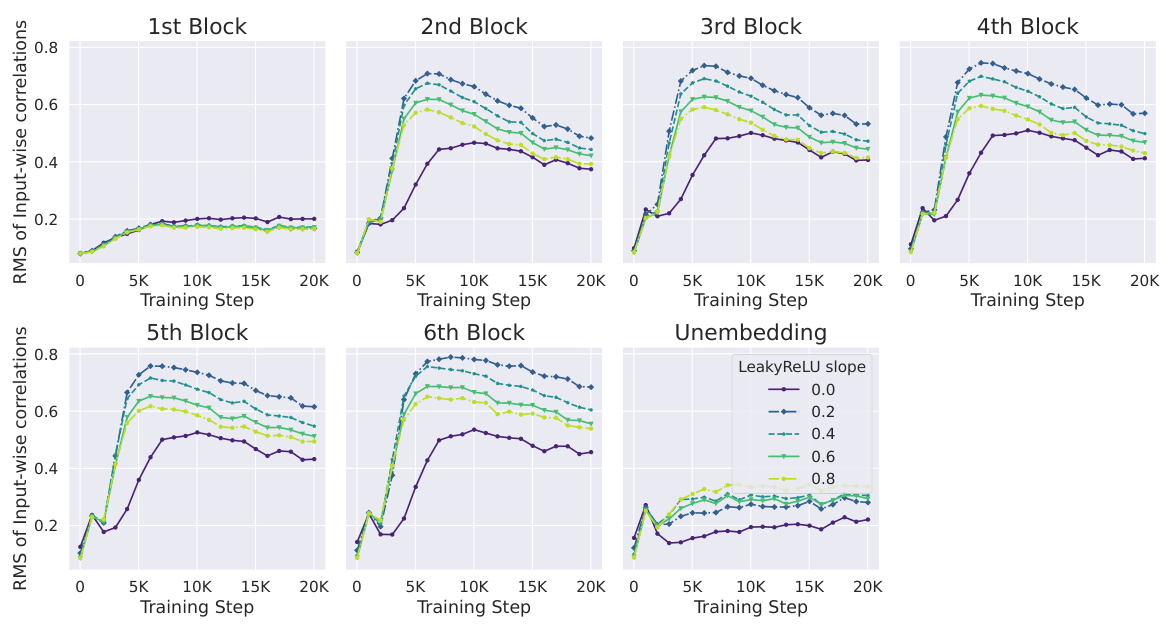
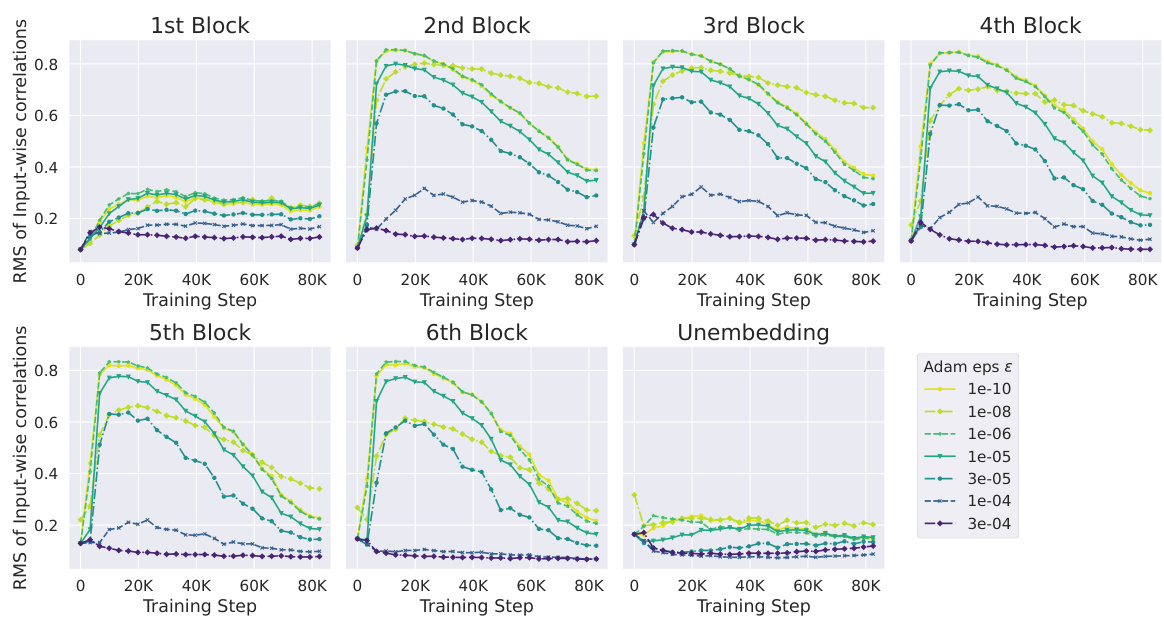
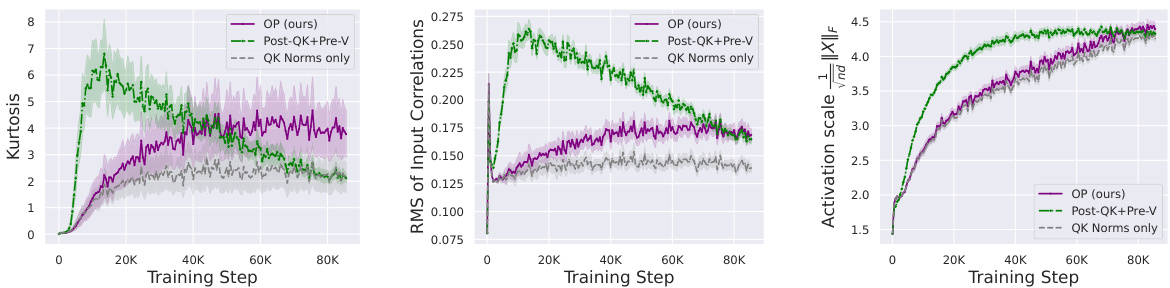
This figure shows the correlation between Outlier Features (OFs), signal propagation, and the effectiveness of downweighting residual branches in mitigating OFs. The left plot demonstrates that Pre-LN layers exhibiting extreme OFE (high activation kurtosis) also exhibit poor signal propagation (high average input-wise correlation), approaching rank collapse. The center-left plot shows that downweighting residual branches improves signal propagation. The right plots show that reducing the residual branch weights leads to significantly lower kurtosis (a measure of OFEs) particularly in earlier layers of the network. The figure highlights the relationship between signal propagation and OFE and suggests that design choices improving signal propagation can mitigate the problem of outlier features.
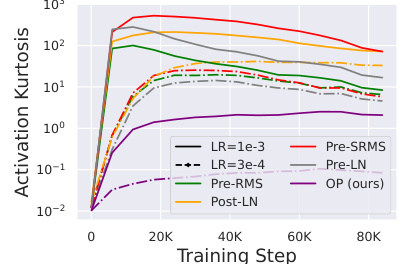
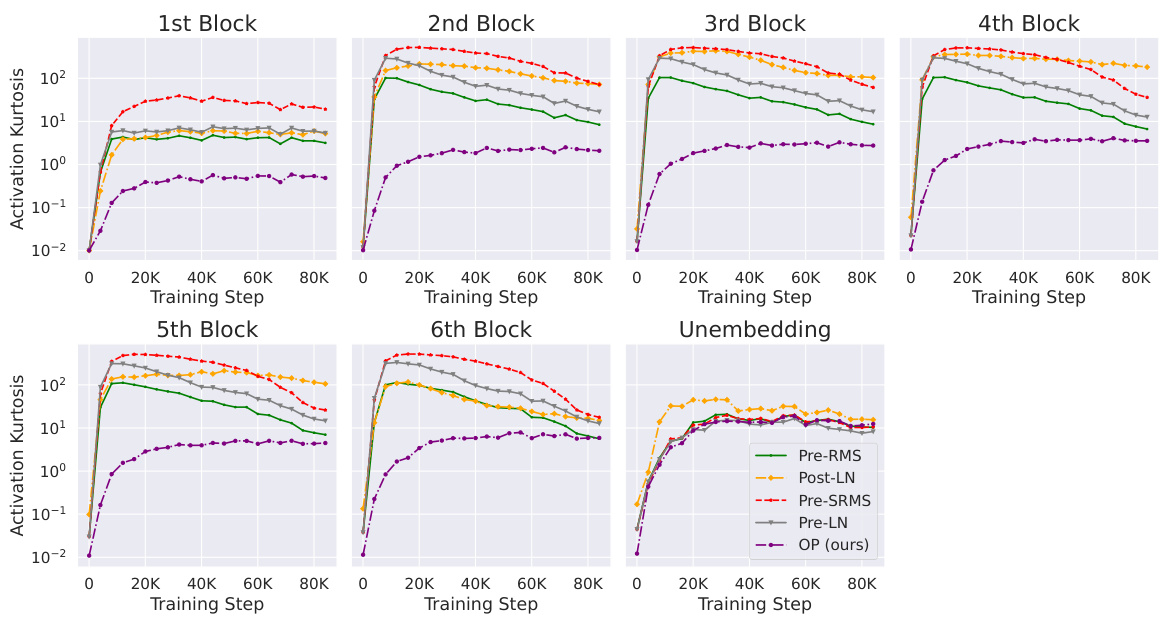
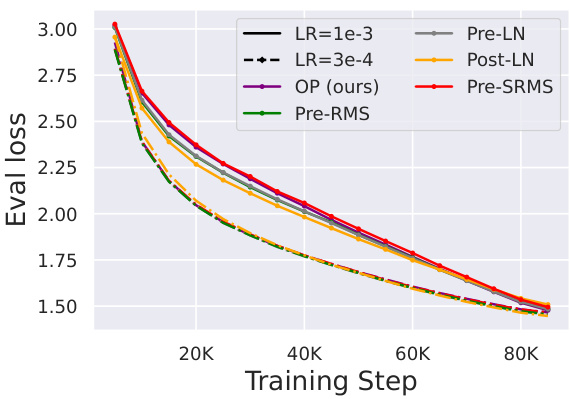
This figure shows that using smaller learning rates (LRs) leads to smaller Outlier Features (OFs) across different transformer blocks. The experiment compares different blocks (Pre-SRMS, Pre-LN, Pre-RMS, OP, Post-LN) trained with different learning rates (1e-3 and 3e-4). The results indicate that smaller learning rates consistently reduce the magnitude of outlier features. This finding suggests that using a smaller learning rate might be a simple way to mitigate the problem of outlier features during training.
This figure shows the impact of different learning rates on the magnitude of Outlier Features (OFs) across various transformer blocks during training. It demonstrates that using smaller learning rates consistently results in smaller OFs, suggesting a potential trade-off between convergence speed and OF mitigation. The results are shown across several different transformer blocks to demonstrate the effect’s generalizability.
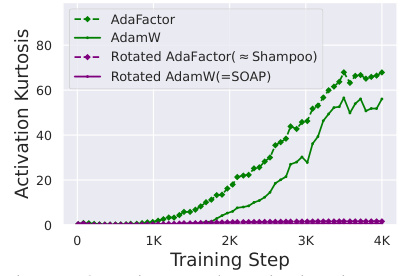
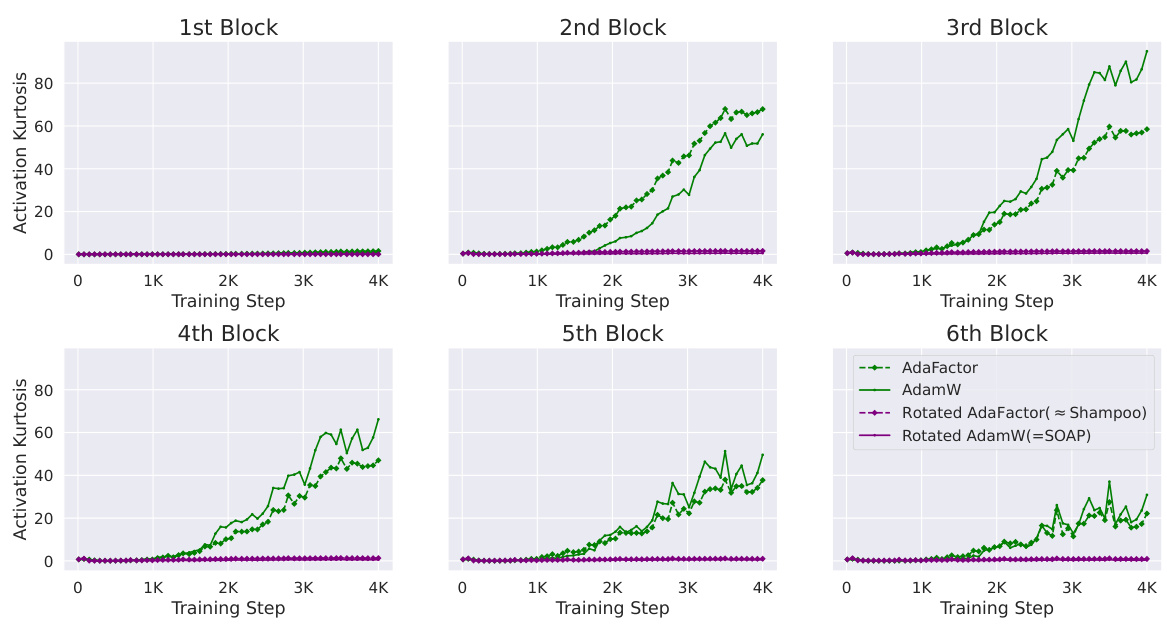
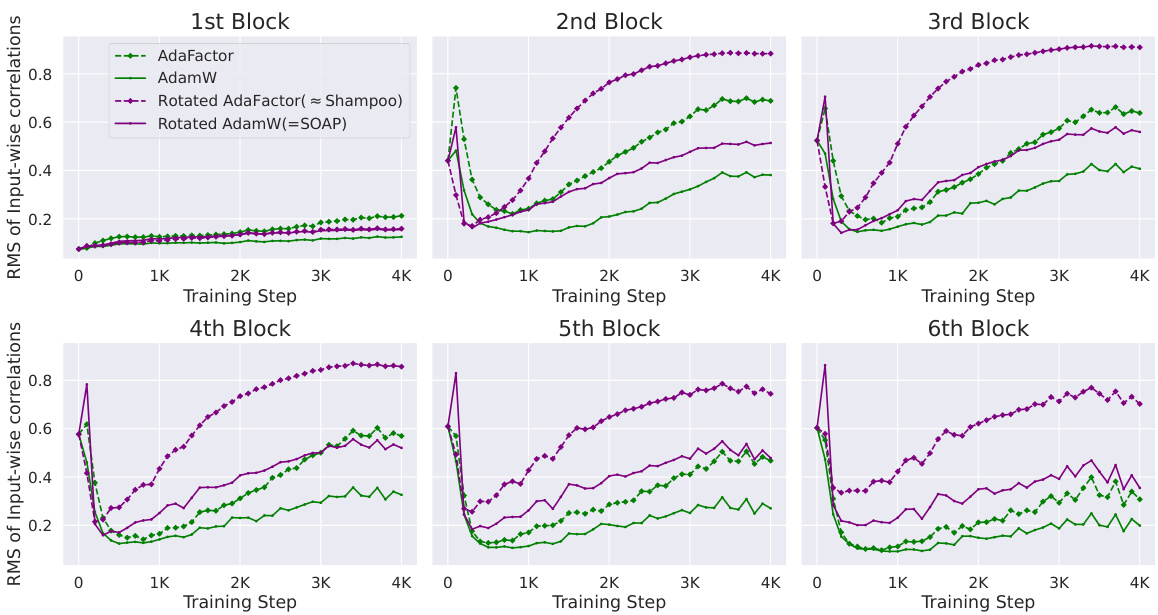
This figure shows the kurtosis values (a measure of outlier features) for different optimizers during the training of a Pre-SRMSNorm transformer model on the CodeParrot dataset. The optimizers compared are AdamW and AdaFactor (both diagonal preconditioners), and their rotated versions using Shampoo’s eigenbasis (rotated AdaFactor and SOAP). The results show that rotating the parameter space before applying diagonal optimization significantly reduces the number of outlier features, regardless of the diagonal preconditioner used. This highlights the potential benefit of using non-diagonal preconditioners for mitigating the emergence of outlier features during training.

This figure displays the loss and kurtosis curves for various models (OP, Pre-Norm, Pre-Norm with modified AdamW) trained with the AdamW optimizer. The left two plots show the training loss for a 1.2B parameter model trained on 90B tokens and a 7B parameter model trained on 6B tokens. The right two plots depict the corresponding kurtosis values. The results demonstrate the consistent impact of the model architecture and hyperparameter choices on outlier features (OFs) even at larger scales.
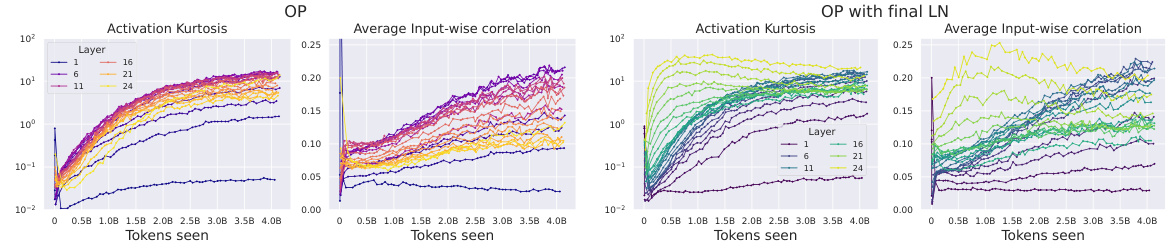
This figure compares the activation kurtosis and average input-wise correlation for different layers in a transformer model. It shows two sets of experiments: one with the Outlier Protected (OP) block and one with the OP block plus a final Layer Normalization (LN) layer before unembedding. The results demonstrate that poor Signal Propagation (high input correlation) is associated with high feature kurtosis (Outlier Features), and that adding a final LN layer exacerbates this issue.

This figure shows the appearance of outlier features in three different sizes of Pythia transformers during training. The x-axis represents the training step, and the y-axis shows the kurtosis of neuron activation RMS, a metric used to quantify outlier features. Each line represents a different layer in the transformer. The figure visually demonstrates that outlier features emerge during standard transformer training across different model sizes, motivating the paper’s investigation into the design choices influencing this phenomenon.

This figure shows the appearance of outlier features in three different sizes of Pythia transformers during training. The outlier features are measured using the kurtosis metric (Eq 1) defined in the paper. The figure visually demonstrates that outlier features emerge during standard transformer training across various model sizes, motivating the research in the paper to understand and minimize their emergence.

This figure compares the activation kurtosis of the residual stream across different layers for both Pre-LN (standard transformer block with Layer Normalization) and OP (Outlier Protected) blocks in a 1.2B parameter transformer model. The results show that the OP block consistently achieves lower activation kurtosis across all layers than the Pre-LN block, indicating a significant reduction in outlier features. This reduction is particularly pronounced in the earlier layers. The y-axis is log-scaled to highlight the magnitude of the difference.
This figure compares the activation kurtosis of the residual stream across different layers of a 1.2B parameter transformer model trained using the OP block and the Pre-LN block. The OP block consistently shows lower activation kurtosis, especially in the earlier layers, indicating that it effectively mitigates outlier features. The peak kurtosis during training is also significantly lower in the OP block compared to the Pre-LN block. This result suggests that the OP block, designed to remove normalisation layers, helps to reduce the magnitude of outlier neuron activations during training. This figure also highlights the fact that removing the final layer normalization (LN) before unembedding can result in higher input correlations and feature kurtosis, even with the OP block.

This figure compares the activation kurtosis of residual streams across layers for the Pre-LN and OP Transformer blocks during training. The OP block consistently shows significantly lower kurtosis than Pre-LN, indicating a substantial reduction in outlier features, especially in the early layers. The shared y-axis highlights the magnitude of this difference. The experiment uses a 1.2B parameter model on the Languini Books dataset, employs a specific AdamW learning rate schedule, and notes that removing the final LN further reduces outlier features.
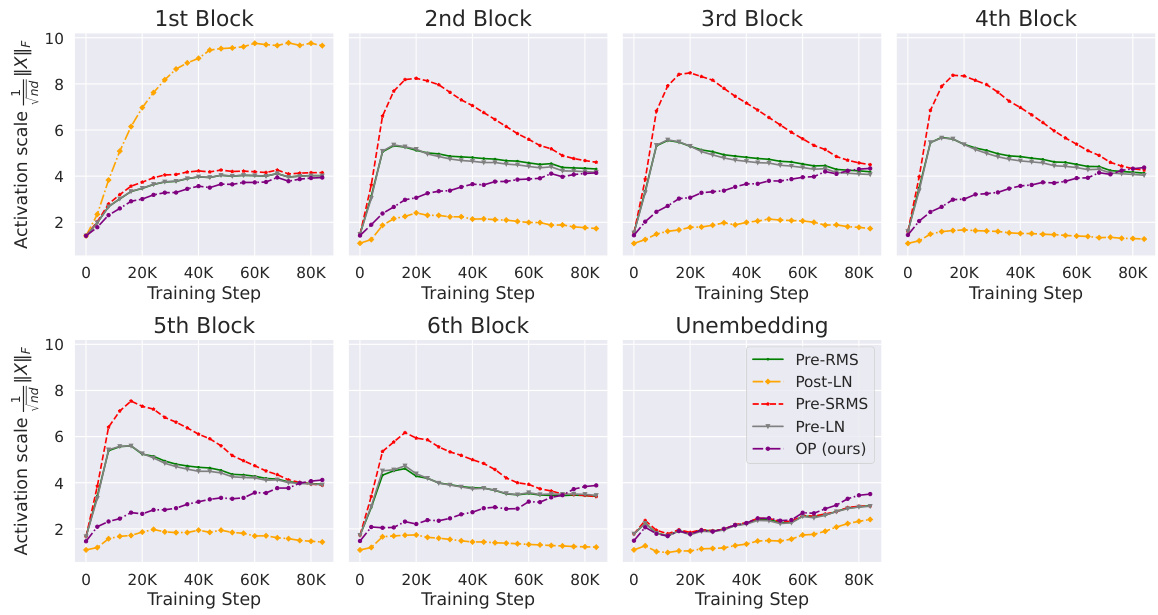
This figure compares the activation kurtosis of residual streams across layers for both OP and Pre-LN Transformer blocks at 1.2B parameter scale on Languini Books dataset. It demonstrates that the proposed OP block significantly reduces the activation kurtosis, especially in early layers, thereby mitigating outlier features (OFs) while maintaining training stability and speed.
The figure displays the outlier features’ appearance in various sizes of open-source transformers during training. It shows that outlier features emerge across multiple layers within the models and that their prevalence varies depending on the transformer’s size and layer depth. The Kurtosis metric (Equation 1) is used to quantify the magnitude of these outlier features.

This figure compares the activation kurtosis of residual streams across different layers in the Pre-LN and OP transformer models. It shows that the OP block consistently reduces kurtosis by several orders of magnitude, especially in earlier layers. This demonstrates that the OP block effectively mitigates outlier features.

This figure compares the activation kurtosis of residual streams across different layers for both the Outlier Protected (OP) block and the standard Pre-LN block in a 1.2B parameter transformer model trained on the Languini Books dataset. The results demonstrate that the OP block consistently exhibits lower kurtosis values, significantly reducing Outlier Features (OFs). This reduction is particularly notable in the earlier layers. The figure also highlights that peak kurtosis during training is always higher in the Pre-LN block than in the OP block. A final layer normalization before unembedding is removed in the OP model, highlighting its impact on OFE.

This figure compares the activation kurtosis (a measure of outlier features) in different layers of a transformer model trained with the proposed Outlier Protected (OP) block and a standard Pre-LN (Pre-Layer Normalization) block. The OP block consistently shows lower kurtosis, indicating fewer outlier features, especially in the early layers. The figure highlights the effectiveness of the OP block in mitigating outlier features during training.
This figure compares the activation kurtosis of residual streams across different layers for the Outlier Protected (OP) block and the standard Pre-LN block at 1.2B parameter scale. It shows that the OP block consistently has lower kurtosis (by up to four orders of magnitude), indicating a significant reduction in outlier features. The peak kurtosis during training is also lower with the OP block. The impact of the final layer normalization (LN) layer on OFE is further investigated in a separate figure (Figure 10).
This figure compares the activation kurtosis of residual streams across layers in Pre-LN and OP transformer blocks at a 1.2B parameter scale. The OP block consistently shows lower kurtosis values, indicating a significant reduction in outlier features. The y-axis uses a log scale, highlighting that the differences are substantial (up to 4 orders of magnitude). The figure suggests that the OP block effectively mitigates the OFE problem without compromising training stability.
This figure compares the activation kurtosis of residual streams across layers for both the Outlier Protected (OP) block and the standard Pre-LN block in a 1.2B parameter transformer model. The y-axis uses a log scale to highlight the consistent difference in kurtosis between the two models across all layers. The results show that the OP block consistently has lower activation kurtosis, indicating fewer outlier features, especially in earlier layers. The peak kurtosis during training is also always higher in the Pre-LN model, further supporting the effectiveness of the OP block in mitigating OFEs.
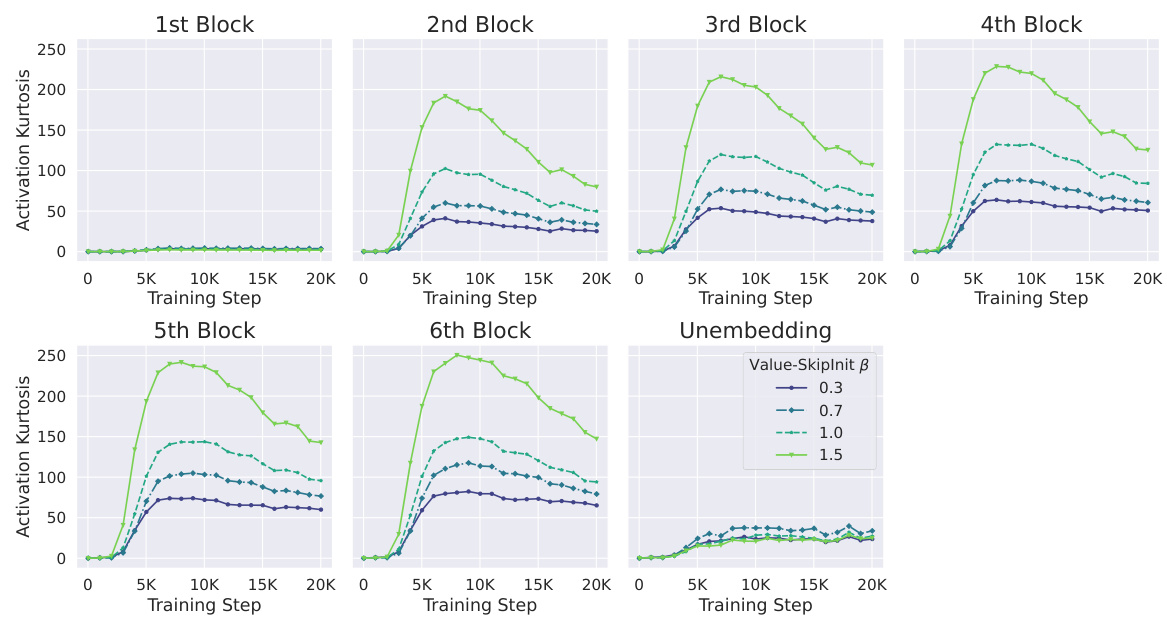
This figure compares the activation kurtosis of residual streams across different layers for both the standard Pre-LN transformer block and the proposed Outlier Protected (OP) block. It shows that the OP block consistently reduces the activation kurtosis across all layers, particularly in the early layers. This reduction in kurtosis, a measure of outlier features, is substantial (up to four orders of magnitude). The figure also illustrates that the peak kurtosis during training is always higher with the Pre-LN block compared to the OP block.
This figure compares the activation kurtosis (a measure of outlier features) of the residual stream across different layers in transformer models with and without the proposed Outlier Protected (OP) block. The results demonstrate that the OP block consistently reduces activation kurtosis compared to the standard Pre-LN block, particularly in earlier layers. It also shows that the peak kurtosis during training is consistently lower with the OP block.

The figure compares the activation kurtosis of the residual stream across layers for the OP block and the Pre-LN block in a 1.2B parameter transformer model trained on the Languini Books dataset. The OP block consistently shows significantly lower kurtosis values compared to the Pre-LN block, especially in the earlier layers. This indicates that the OP block effectively mitigates outlier features.
The figure shows the impact of learning rate on the Outlier Features (OFs) across different transformer blocks. Smaller learning rates (LRs) consistently lead to smaller OFs, suggesting a relationship between learning rate and the magnitude of outlier neuron activations. This finding highlights the importance of careful learning rate selection in mitigating the negative impact of outlier features during transformer training.

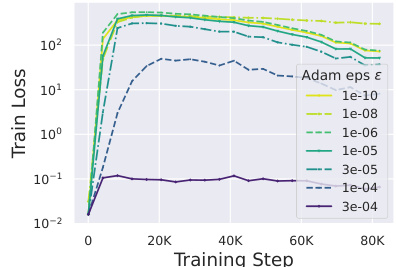
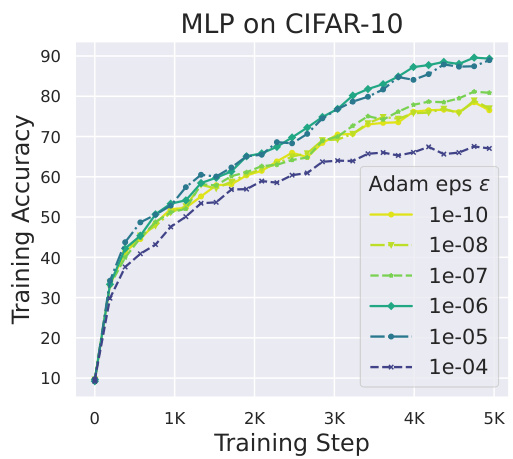
This figure shows the impact of the Adam epsilon (e) hyperparameter on Outlier Features (OFs) during training. The experiment was conducted on a 130M parameter model trained on the CodeParrot dataset. The plot shows the kurtosis (a measure of OFs) across various layers of the model for different values of the Adam epsilon. The results indicate that increasing the epsilon value from 1e-6 to 3e-4 monotonically reduces the OFs. Below 1e-6, changes in epsilon have a less significant impact on OFs.
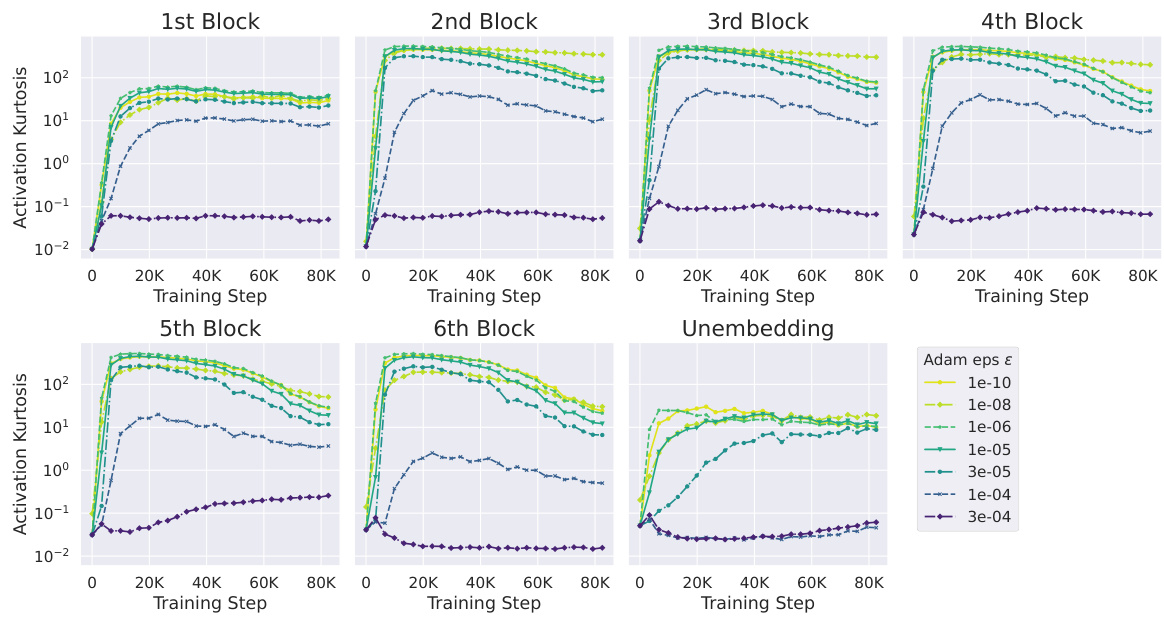
This figure shows the impact of the Adam epsilon (e) hyperparameter on outlier features (OFs) across different layers of a transformer model. The experiment was conducted on the CodeParrot dataset with a model size of 130 million parameters. The results indicate that increasing the epsilon value reduces the kurtosis, a measure of the heavy-tailedness of the activation distribution, thereby mitigating the presence of outlier features. The effect is more pronounced when increasing the epsilon from 1e-6 to 3e-4. Below 1e-6, varying the epsilon hyperparameter has less of an impact on OFs.
The figure compares the activation kurtosis of residual streams across layers for models with Pre-Norm (Pre-LN) and Outlier Protected (OP) blocks. The OP block consistently shows significantly lower kurtosis (up to four orders of magnitude) than Pre-LN, especially in the earlier layers, indicating a substantial reduction in Outlier Features (OFs). The results demonstrate the effectiveness of the OP block in mitigating OFE, particularly in early training stages, without sacrificing convergence speed.
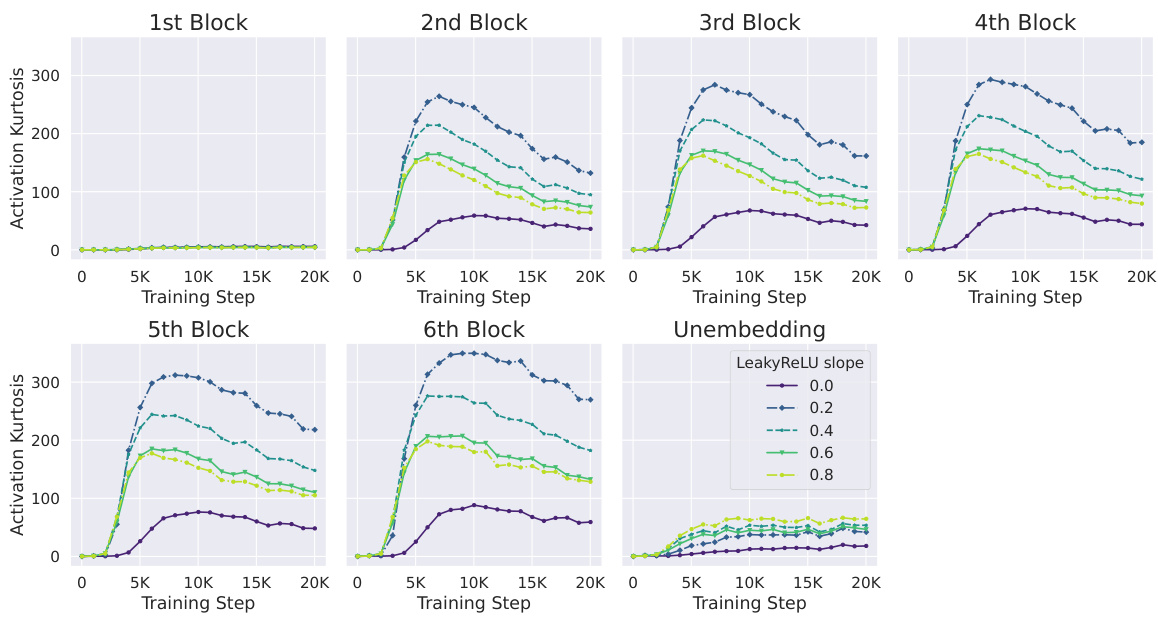
The figure shows the kurtosis of neuron activation norms for different normalization layers (LN, RMSNorm, and SRMSNorm) in pre-norm and post-norm transformer blocks during training. The kurtosis metric measures the presence of outlier features. The plot shows that outlier features emerge regardless of the type of normalization layer used, highlighting the robustness of this phenomenon. It is part of a study to investigate the causes of outlier feature emergence during transformer training.

This figure compares the training loss curves of four different optimizers: AdaFactor, AdamW, Rotated AdaFactor (approximated as Shampoo), and Rotated AdamW (SOAP). The results are presented to show the relative convergence speeds and training stability, highlighting the performance improvement of the non-diagonal preconditioners (Rotated AdaFactor and SOAP) over the diagonal preconditioners (AdaFactor and AdamW). This supports the paper’s findings regarding the effect of optimization choices on outlier features and training efficiency.
The figure displays graphs showing the emergence of Outlier Features (OFs) during the training of three different sizes of the Pythia transformer models. The x-axis represents the training step, and the y-axis shows the kurtosis of neuron activation norms, a metric used to quantify OFs. The different lines in each graph correspond to different layers within the transformer model. The figure highlights that OFs are a common phenomenon in standard transformer training, motivating the research presented in the paper to understand and minimize their occurrence.
The figure shows the appearance of outlier features in three different sizes of Pythia transformer models during training. The x-axis represents the training step, and the y-axis represents the kurtosis of neuron activation norms. High kurtosis indicates the presence of outlier features. Each plot shows the kurtosis across different layers of the network. The observation is that outlier features consistently emerge during training, highlighting the problem addressed in the paper.

This figure shows the emergence of Outlier Features (OFs) in three different sizes of the Pythia transformer models during training. The x-axis represents the training step, and the y-axis shows the kurtosis of neuron activation RMS which measures OFs. The plot demonstrates that OFs emerge during the training process across different scales of transformer models. The paper uses this as evidence to study the design choices that cause OFs and methods to mitigate them.
The figure shows the kurtosis of neuron activations during training for different normalization layers (Pre-LN, Post-LN, Pre-RMS, Pre-SRMS) in a 130M parameter transformer model. It demonstrates that the emergence of outlier features (OFE) is prevalent across various normalization methods, highlighting the impact of normalization layers on the phenomenon. Notably, a newly introduced ‘OP’ (outlier protected) block shows significantly lower kurtosis compared to other approaches.

This figure shows that using smaller learning rates during training leads to a reduction in outlier features (OFs) across different transformer blocks. The plot likely displays the kurtosis (a measure of OFs) over training steps for several different transformer architectures, demonstrating the consistent effect of reduced learning rates on OF mitigation.
This figure shows the impact of using smaller learning rates on the occurrence of outlier features (OFs) in different transformer blocks. The results indicate that reducing the learning rate consistently leads to a decrease in the magnitude of outlier features, suggesting that smaller learning rates mitigate the formation of OFs during training.
This figure shows the presence of outlier features in three different sizes of Pythia transformers during training. The outlier features are measured by Kurtosis, which is a statistical measure of the ’tailedness’ of the probability distribution of the data. The figure shows that outlier features emerge during the training process of all three sizes of transformers, highlighting the need to investigate the design choices that influence their emergence.

The figure shows the average kurtosis across the 12 residual stream layers of Vision Transformers (ViTs) trained on ImageNet-1K. Three different ViT transformer blocks are compared: Pre-LN, Pre-LN with LayerScale, and the proposed Outlier Protected (OP) block. The plot visualizes how the average kurtosis changes over epochs for each model, providing insights into the presence of outlier features during training. LayerScale is shown to reduce kurtosis compared to standard Pre-LN. The OP block demonstrates even lower kurtosis.

This figure shows the test accuracy (top 1%) on ImageNet-1k for three different ViT models: OP, Pre-LN, and Pre-LN with LayerScale. The results demonstrate that the OP (Outlier Protected) block does not negatively impact the performance of the ViT model and achieves comparable accuracy to standard architectures. The slightly higher accuracy in OP might suggest that the mitigation of outlier features may have a positive impact on performance, even if it isn’t statistically significant.

This figure compares the activation kurtosis of residual streams across different layers in Pre-LN and OP transformer blocks at 1.2B parameter scale. It shows that the OP block consistently and significantly reduces kurtosis across all layers compared to the Pre-LN block, especially in early layers. The y-axis is log-scaled to highlight the magnitude of the reduction, which is up to 4 orders of magnitude. The figure also demonstrates that the peak kurtosis during training is always higher in Pre-LN than in the OP block.

The figure shows that removing the entropy regularization mechanism in the outlier protected (OP) block leads to training failure, indicated by a sharp increase in training loss. Using a different entropy regularization method (tanh) prevents failure but slows convergence. The results highlight the importance of entropy regulation for stability during transformer training.
This figure compares the activation kurtosis of residual streams across layers for both the Outlier Protected (OP) block and the standard Pre-LN block. The OP block consistently shows significantly lower kurtosis, indicating a substantial reduction in outlier features, particularly in the early layers. The results demonstrate that the OP block effectively mitigates OFE without sacrificing training speed or stability.

The figure shows a comparison of activation kurtosis across different layers of a transformer model with and without the Outlier Protected (OP) block. The OP block consistently demonstrates lower kurtosis values, especially in early layers, indicating a significant reduction in outlier features. The results highlight the effectiveness of the OP block in mitigating outlier features without impacting convergence speed.
This figure compares the activation kurtosis of residual streams across layers in two different transformer blocks: Pre-LN (Pre-Norm with Layer Normalization) and OP (Outlier Protected). It demonstrates that the OP block consistently reduces activation kurtosis (a measure of outlier features) across all layers, especially in early layers, compared to the Pre-LN block. The results highlight that the OP block effectively mitigates outlier features without sacrificing training speed or stability.
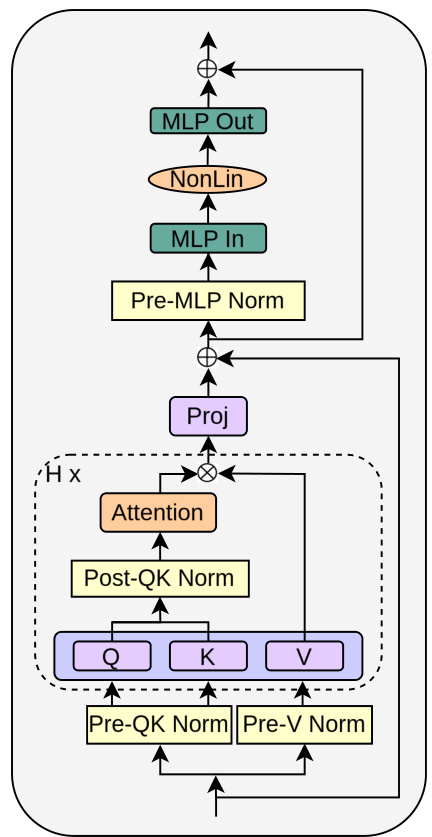
This figure shows the architecture of the proposed Outlier Protected (OP) Transformer block. The key differences from standard Pre-Norm blocks are the removal of normalization layers before both the attention and MLP sub-blocks and the addition of three components: 1) downscaling of residual branches using a trainable scalar β; 2) an entropy regulation mechanism to prevent entropy collapse (like QK-Norm); and 3) (optionally) scaling of MLP inputs before the nonlinearity using a trainable scalar α. The figure illustrates how these modifications combine to mitigate the formation of outlier features.
This figure compares the activation kurtosis of residual streams across different layers for both the OP block and the standard Pre-LN block. The results show that the OP block consistently exhibits lower kurtosis, particularly in earlier layers, indicating a significant reduction in outlier features (OFs). The differences are several orders of magnitude across training steps. It also highlights that the default Pre-LN models always exhibit a higher peak kurtosis during training.

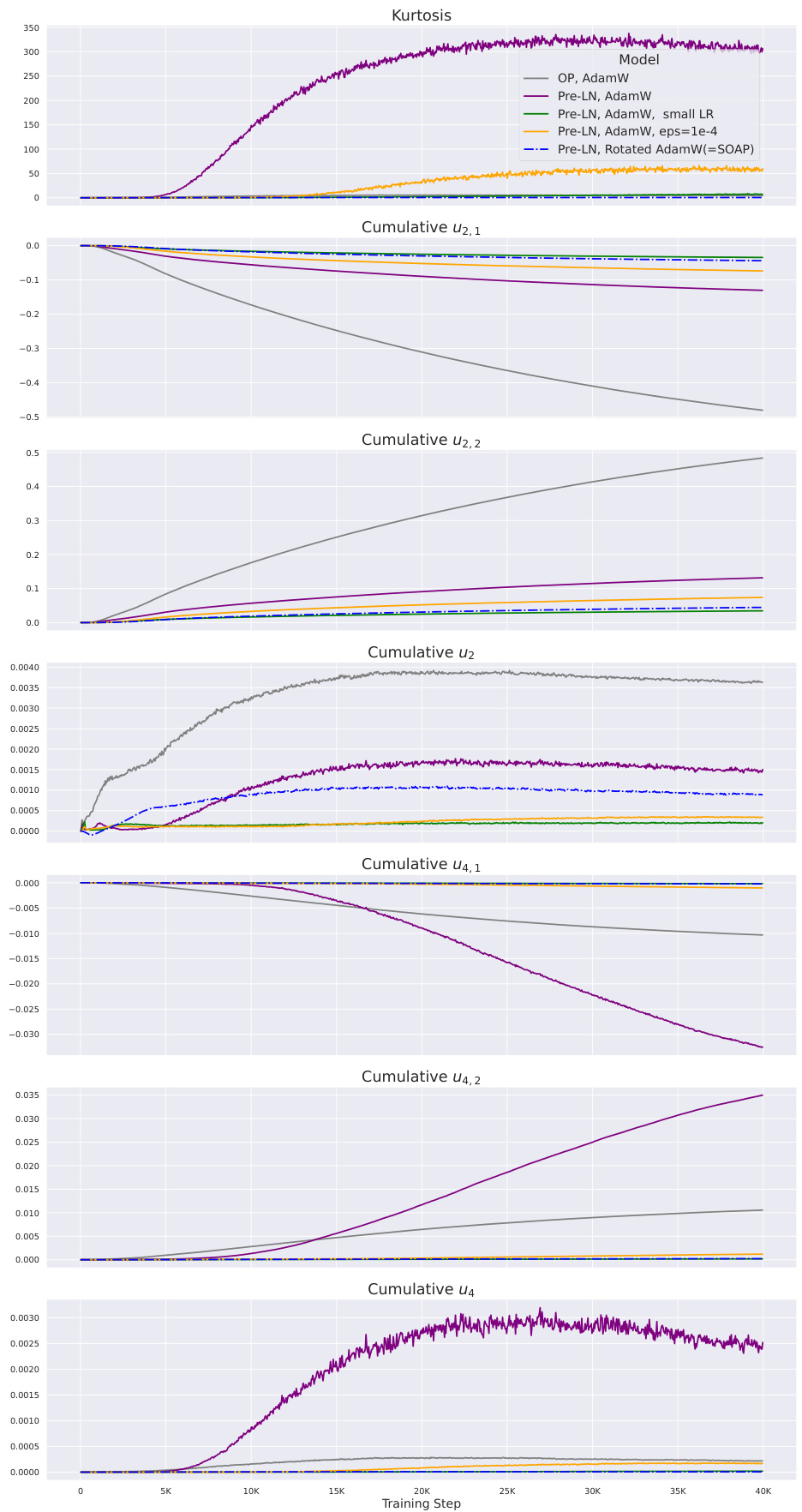
The figure shows the cumulative sums of different order terms that contribute to the changes in the second and fourth moments of neuron activations during training. These changes are directly related to the kurtosis, a measure of the ’tailedness’ of the distribution. The plot compares different model configurations (OP, Pre-LN, and variations of Pre-LN with different hyperparameter settings), highlighting how the quadratic term in the fourth-moment update is often the dominant factor driving the increase in kurtosis, particularly in the Pre-LN models. Reducing the learning rate, increasing the Adam epsilon, or using a non-diagonal preconditioner (SOAP) all reduce the magnitude of this dominant quadratic term.

The figure compares the activation kurtosis in different layers of a transformer model with and without the proposed Outlier Protected (OP) block. The results show that the OP block significantly reduces the activation kurtosis across all layers, especially in the early layers, demonstrating its effectiveness in mitigating outlier features.

The figure shows the cumulative values of different terms that contribute to the kurtosis updates during training. It compares these values for various model configurations, including an Outlier Protected (OP) model and standard Pre-LN models with and without modifications (small learning rate, increased epsilon in Adam, and using SOAP). The results indicate that the quadratic term (u4,2) is the primary driver of the increase in kurtosis in the standard Pre-LN model, while modifications that reduce OFs also reduce this quadratic term.
More on tables
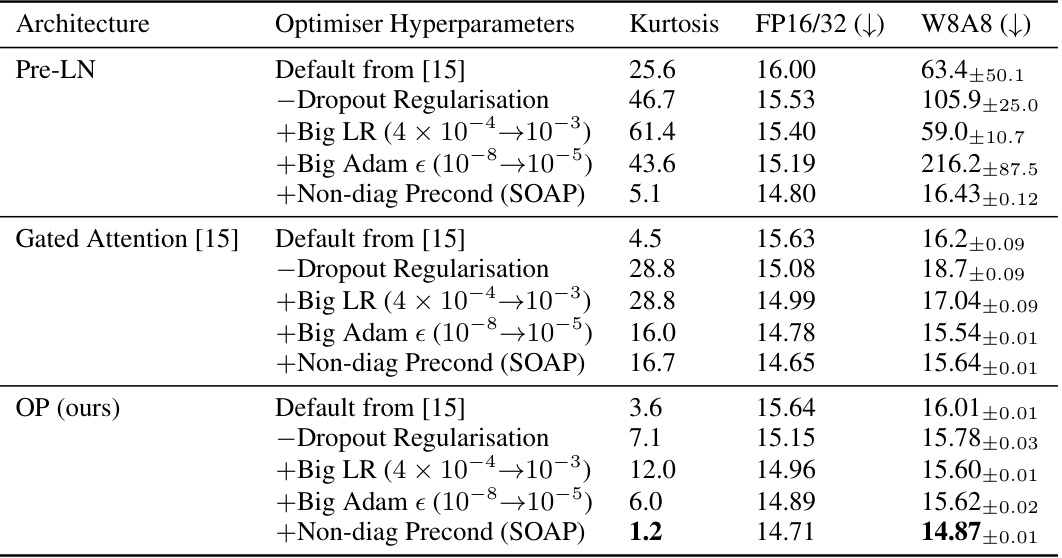
This table shows the results of quantization experiments on the OPT-125m model. Different model architectures (Pre-LN, Gated Attention, OP) and optimizer hyperparameters are compared. The table reports the average kurtosis across layers, standard precision perplexity (FP16/32), and quantized int8 perplexity (W8A8). The key finding is that the combination of the OP architecture and the SOAP optimizer achieves the lowest quantized perplexity, demonstrating the effectiveness of the proposed methods for minimizing outlier features and improving quantization.

This table presents the results of an experiment on quantizing OPT-125m models. It shows the average kurtosis across layers, standard precision perplexity (FP16/32), and quantized int8 perplexity (W8A8) for various model architectures and optimization choices. The results demonstrate a strong correlation between kurtosis and int8 error. The best performing int8 setup uses the proposed Outlier Protected (OP) block and SOAP optimizer.
This table presents the results of experiments evaluating different model architectures and optimization strategies on the task of quantizing OPT-125m language models. The table compares standard precision perplexity (FP16/32) and int8 quantized perplexity (W8A8), along with the average kurtosis across layers. The results show a strong correlation between kurtosis (a measure of outlier features) and int8 quantization error. The combination of the Outlier Protected (OP) block and the SOAP optimizer yields the lowest kurtosis and the smallest increase in perplexity after quantization.
Full paper#



















