TL;DR#
Reinforcement learning (RL) heavily relies on value-based methods. However, occupancy functions, representing state visitation densities, offer potential advantages in exploration, handling distribution shifts, and optimizing various objectives beyond the expected return. Existing efficient policy optimization methods using only occupancy functions are scarce, and offline RL faces challenges with non-exploratory data. This limits the applicability and effectiveness of occupancy functions in real-world scenarios.
This research introduces novel model-free policy gradient algorithms leveraging occupancy functions for online and offline RL. The algorithms elegantly transform gradient estimation into a series of computationally efficient squared-loss regressions, eliminating the need for value function approximation. Furthermore, the proposed methods are theoretically sound, featuring convergence analysis that accounts for finite-sample estimation error and data coverage. Notably, they naturally accommodate arbitrary offline data distributions and extend to optimizing any differentiable objective functional.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between the theoretical understanding of occupancy functions and their practical application in RL, particularly addressing the computational challenges and handling non-exploratory offline data. It opens avenues for optimizing general objectives beyond expected return and advancing offline RL methods.
Visual Insights#
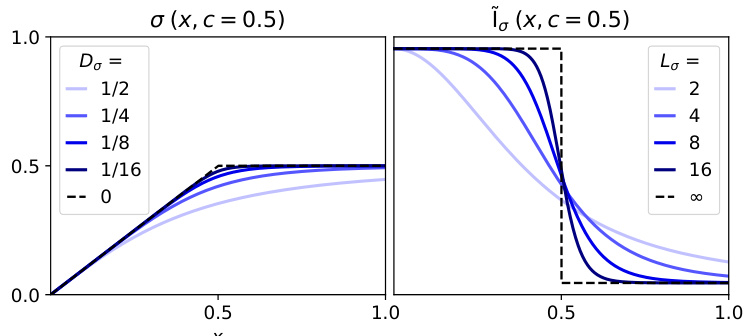
🔼 This figure shows plots of the smooth clipping function σ(x, c) and its derivative ĩσ(x, c) for different values of the smoothness parameter β. The plots illustrate the trade-off between how well σ(x, c) approximates the hard clipping function (x ∧ c) (smaller Dβ) and the smoothness of its gradient (smaller Lβ). The dashed black line in each plot represents the hard clipping function and its derivative for comparison.
read the caption
Figure 1: We plot σ(x, c) from Prop. 4.3 for different b, that trade-off between clipping approximation error and smoothness (D x 1/Lo).
In-depth insights#
Occupancy PG#
The concept of “Occupancy PG” introduces a novel approach to policy gradient methods in reinforcement learning (RL) by directly leveraging occupancy functions. This represents a significant departure from traditional value-based methods. By focusing on the state visitation distribution (occupancy) rather than value functions, Occupancy PG offers several key advantages. Firstly, it simplifies the gradient estimation process, reducing it to a squared-loss regression, thereby enhancing computational efficiency. Secondly, it provides a more flexible framework capable of handling diverse objective functions beyond expected return, including those not easily formulated with value functions. Thirdly, Occupancy PG presents a robust approach for both online and offline RL, naturally adapting to non-exploratory data in offline settings. However, the effectiveness of Occupancy PG hinges on the accuracy of occupancy function estimation and the challenges related to handling insufficient data coverage in offline scenarios. Further research is warranted to thoroughly investigate the impact of these factors and explore potential improvements.
Online vs Offline RL#
Reinforcement learning (RL) is broadly categorized into online and offline paradigms, each presenting unique challenges and opportunities. Online RL involves an agent continuously interacting with an environment, learning and adapting its policy in real-time. This approach allows for immediate feedback and dynamic policy adjustments, making it suitable for scenarios where the environment is constantly changing or unknown. However, online RL necessitates careful exploration strategies to avoid detrimental actions and ensure efficient learning, potentially at the cost of immediate performance. In contrast, offline RL utilizes a pre-collected dataset of interactions to train a policy. This eliminates the need for real-time interaction, enabling the use of computationally intensive techniques and the possibility of learning from large, diverse datasets. Offline RL is particularly useful for safety-critical applications where real-time experimentation is unacceptable. However, offline RL faces the significant hurdle of extrapolation: the trained policy’s performance in unseen situations may be unreliable and unpredictable, and it’s more prone to issues related to coverage and distributional shift. Choosing between online and offline RL involves carefully considering the specific characteristics of the environment, the availability of data, and the constraints imposed by safety and real-time performance considerations.
Smooth Clipping#
The concept of “Smooth Clipping” in the context of offline occupancy-based policy gradient methods addresses a critical challenge: the unboundedness of density ratios when offline data lacks sufficient coverage. Directly using density ratios from limited data can lead to unstable or unreliable gradient estimates. Smooth clipping mitigates this by introducing a smooth approximation of the hard clipping function used in previous methods. This smooth approximation prevents the unboundedness of density ratios and enhances the robustness of gradient estimation, particularly in scenarios with non-exploratory offline data. The method carefully balances bias and variance trade-offs by controlling how aggressively the occupancies are clipped. The choice of smoothing function is crucial, requiring properties like monotonicity and smooth gradients to guarantee estimation and convergence properties, and theoretical analysis shows that it effectively trades off bias and variance. The resulting algorithm, OFF-OCCUPG, is demonstrably more stable and produces reliable gradient estimates, even when dealing with limited or non-exploratory data. The smooth clipping approach significantly improves the practical applicability of occupancy-based policy gradient methods, overcoming a critical limitation encountered when relying solely on hard-clipped versions.
Convergence Rates#
Analyzing convergence rates in machine learning research is crucial for understanding algorithm efficiency. Tight bounds on convergence rates offer valuable insights into the algorithm’s practical performance and scalability. The analysis often involves examining the algorithm’s ability to reduce error over iterations, using techniques like gradient descent, stochastic gradient descent, or other optimization methods. Factors influencing convergence rates include the choice of optimization algorithm, learning rate, data characteristics (e.g., dimensionality, noise), and the specific problem being solved (convexity, smoothness, etc.). Understanding the convergence rate helps researchers compare different algorithms, choose appropriate hyperparameters, and assess the algorithm’s generalization ability. Theoretical convergence analysis provides guarantees on algorithm performance under specific assumptions and allows researchers to understand algorithm behavior before extensive experimentation. Empirical evaluation of convergence rates confirms theoretical findings and reveals how the algorithm performs under real-world conditions. Challenges in analyzing convergence rates exist when dealing with complex models, non-convex objective functions, high-dimensional data, and stochasticity inherent in the process. The gap between theoretical and empirical convergence can arise due to simplifying assumptions in theoretical analysis and real-world factors not captured by such analysis. Ultimately, a deep understanding of convergence rates is vital for building robust and efficient machine learning systems.
Future Work#
The paper’s “Future Work” section implicitly suggests several promising research avenues. Extending the occupancy-based policy gradient methods to handle continuous action spaces is crucial for broader applicability. Addressing the limitations of offline policy optimization under poor data coverage warrants further investigation, particularly exploring alternative data augmentation or bias mitigation techniques. Developing tighter bounds and relaxing assumptions in the theoretical analysis would enhance the practical value of the presented methods. Finally, given the elegance of applying occupancy functions to diverse RL problems, empirical evaluations on a wider range of tasks—including safety-critical domains and those with complex reward structures—could solidify the efficacy and practical impact of this novel approach. Furthermore, investigating the connection between occupancy-based methods and existing techniques like importance weighting or marginalized importance sampling could uncover synergies and potentially lead to more efficient and robust algorithms. Overall, exploring these avenues would significantly expand the current understanding and practical applications of occupancy functions in reinforcement learning.
More visual insights#
More on figures
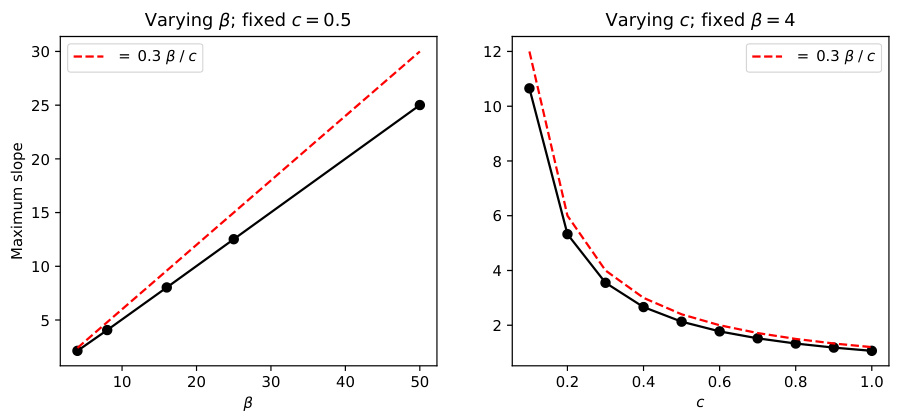
🔼 This figure shows plots of the smooth clipping function σ(x,c) for different values of the parameter β and the clipping constant c. The smooth clipping function σ(x, c) is an approximation of the hard clipping function min(x, c) that is used in the paper’s offline policy gradient algorithm. The plots illustrate the trade-off between the approximation error and the smoothness of the gradient of the smooth clipping function. The approximation error is the difference between the smooth clipping function and the hard clipping function. The smoothness is measured by the Lipschitz constant of the gradient of the smooth clipping function. The plots show that as β increases, the approximation error decreases but the smoothness of the gradient decreases. Conversely, as c increases, the approximation error increases but the smoothness of the gradient increases.
read the caption
Figure 1: We plot σ(x, c) from Prop. 4.3 for different b, that trade-off between clipping approximation error and smoothness (D x 1/Lo).
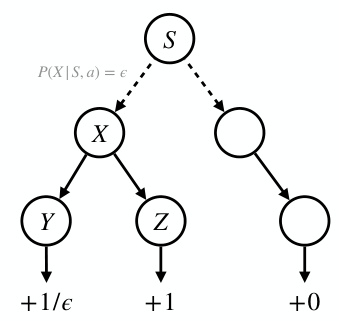
🔼 This figure is a simple MDP example used in Proposition C.3 to demonstrate that even with all-policy coverage in the offline setting, the optimality gap can still be large if the initial state distribution is not sufficiently exploratory. The MDP consists of a root node S, which transitions to either node X or another node with probability ε. Node X then transitions to either node Y or Z. Nodes Y and Z are terminal nodes with rewards 1/ε and 1 respectively. The other node transitions to another terminal node with reward 0. This example highlights the importance of sufficient data coverage for offline policy optimization, illustrating that even when all policies are represented in the data, the performance might still be far from optimal if the coverage is not sufficient in reward-relevant states.
read the caption
Figure 3: Example in Prop. C.3
Full paper#



















