TL;DR#
Neural image compression, while advancing rapidly, faces challenges due to imperfect optimization and limitations in model capacity. Existing methods like Stochastic Gradient Gumbel Annealing (SGA) aim to refine latents (compressed image representations) but have limitations. This leads to suboptimal compression performance.
This research presents SGA+, an enhanced version of SGA, to overcome these issues. SGA+ includes three refined methods which show improved compression performance via rate-distortion trade-offs. The best-performing method improves compression performance on both Tecnick and CLIC datasets, and is less sensitive to hyperparameters. Experiments confirm its superior performance and generalization across datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel method, SGA+, for improving the performance of neural image compression models. This addresses a critical limitation of existing methods and opens avenues for more efficient and effective image compression techniques. The findings are relevant to researchers working on image compression, deep learning, and related fields.
Visual Insights#

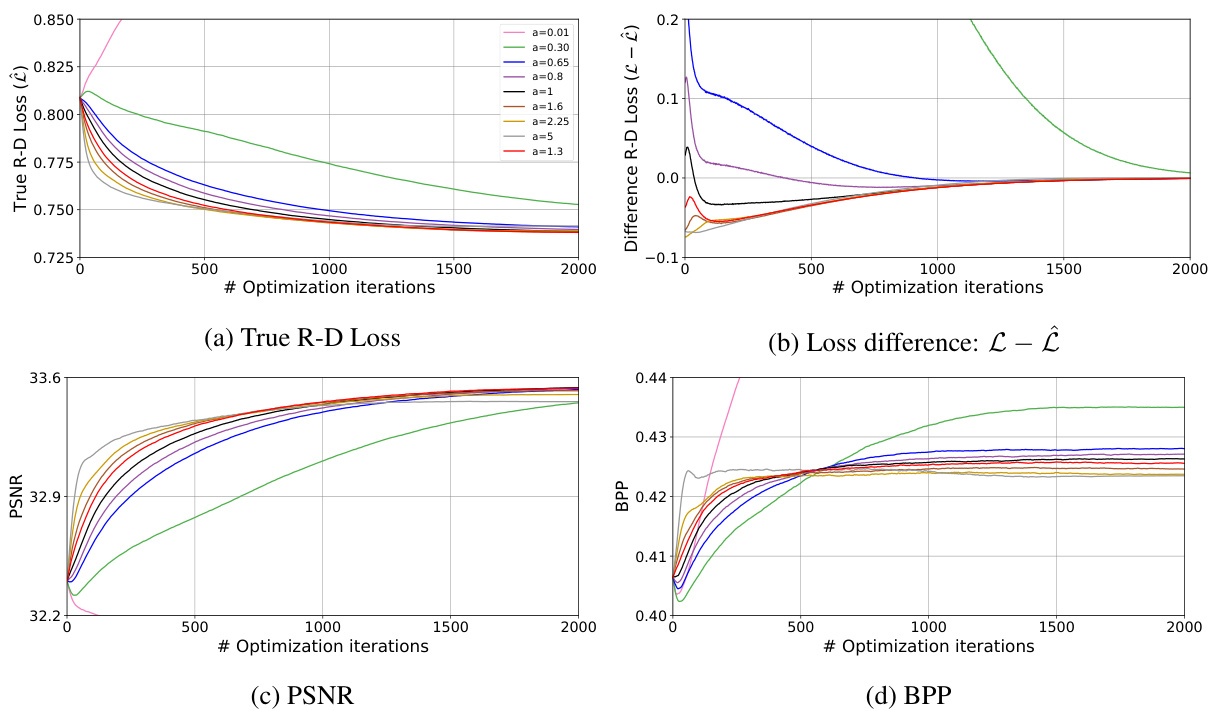
🔼 This figure visualizes the probability space for different methods used in the paper for both two-class and three-class rounding. Subfigure (a) compares the probability of flooring ([v]) and ceiling ([v]) for atanh, linear, cosine, and sigmoid scaled logit (SSL) methods. The atanh function shows steeper gradients near 0 and 1, while the other methods provide smoother transitions. Subfigure (b) extends the linear method to three-class rounding, showcasing the probabilities for rounding down ([v]-1), to the nearest integer ([v]), and up ([v]+1). The dotted lines in (b) represent three-class rounding while the solid lines represent the standard two-class rounding. The figure highlights how different probability space functions influence the gradients during optimization of the latents. The aim is to find probabilities that reduce the gradient saturation and vanishing gradients found in the atanh function.
read the caption
Figure 1: Probability space for (a) Two-class rounding (b) Three-class rounding

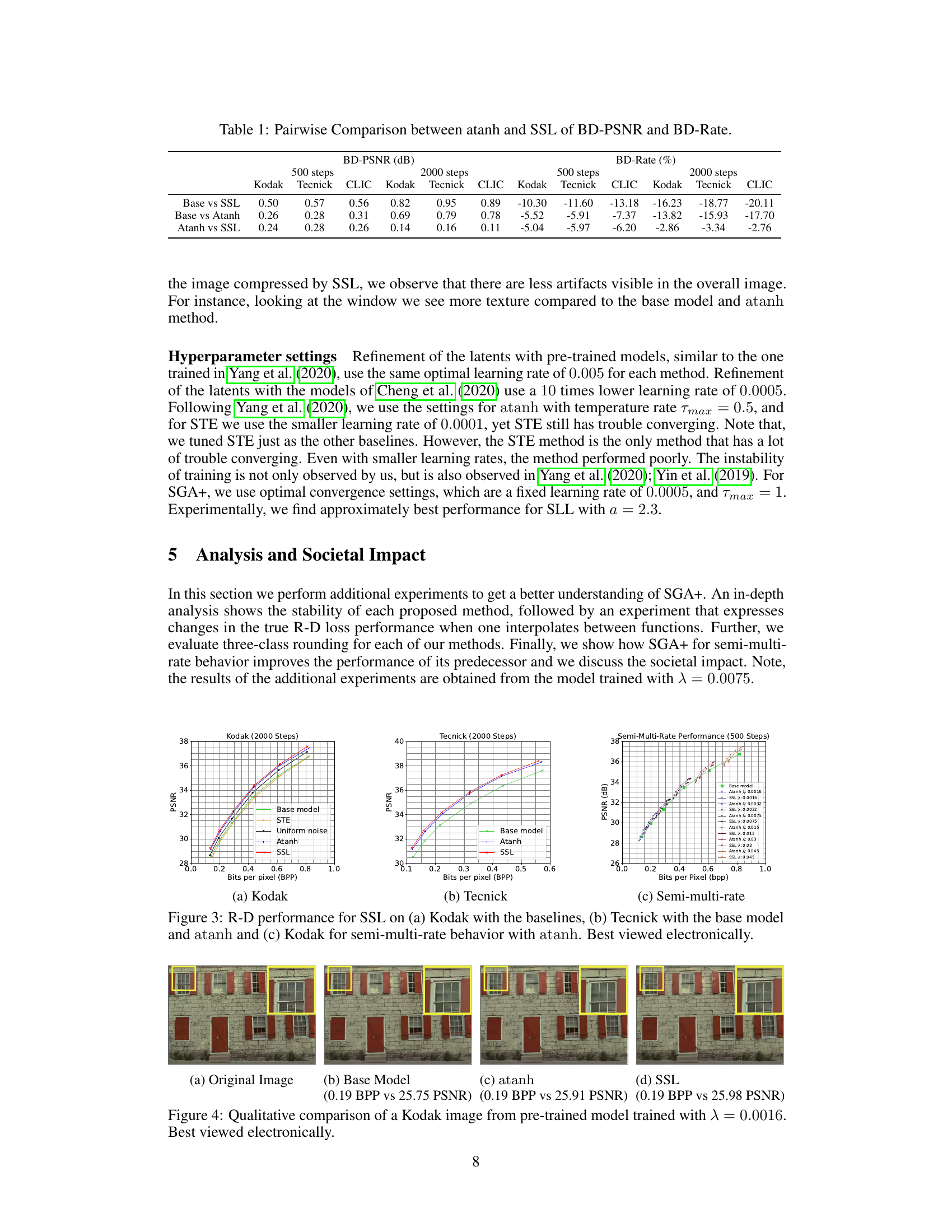
🔼 This table presents a pairwise comparison of the BD-PSNR (Bjontegaard Delta Peak Signal-to-Noise Ratio) and BD-Rate (Bjontegaard Delta Rate) between the atanh and SSL methods. The comparison is made across three datasets (Kodak, Tecnick, and CLIC) and for two different numbers of optimization iterations (500 and 2000). BD-PSNR is a measure of the improvement in image quality, while BD-Rate indicates the improvement in compression efficiency. Positive values indicate that SSL outperforms atanh, and negative values indicate that atanh is better.
read the caption
Table 1: Pairwise Comparison between atanh and SSL of BD-PSNR and BD-Rate.
In-depth insights#
Latent Optimization#
Latent optimization, in the context of neural image compression, tackles the problem of suboptimal results stemming from imperfect optimization and limitations in encoder/decoder capacities of neural compression models. These models encode images into quantized latent representations, which are then decoded to reconstruct the image. The goal of latent optimization is to improve these latent representations to achieve a better rate-distortion trade-off. Imperfect optimization during the initial training of the neural compression model is a primary reason why latent optimization is needed. The limited capacity of the encoder and decoder prevents the model from achieving optimal latent representations. Methods like Stochastic Gradient Gumbel Annealing (SGA) and its extensions, such as SGA+, aim to refine the latent representations after the model is trained, achieving better results without retraining. This is crucial because retraining the entire model is computationally expensive. Different latent optimization methods employ various techniques to refine latents, improving the balance between compression rate and reconstruction quality. The choice of optimization technique and its associated hyperparameters significantly impact the final compression performance. Thus, careful consideration and evaluation of various latent optimization techniques are essential to achieve efficient and high-quality neural image compression.
SGA+ Methods#
The heading ‘SGA+ Methods’ suggests an extension of the Stochastic Gradient Gumbel Annealing (SGA) technique. SGA is a method used for refining latent representations in neural image compression models, aiming to improve rate-distortion performance by reducing the discretization gap between continuous latent variables and their discrete representations. SGA+ likely introduces novel methods that build upon SGA, potentially addressing limitations such as sensitivity to hyperparameters and the inherent instability of atanh-based probability calculations. These new methods might involve alternative probability functions (e.g., linear, cosine, sigmoid-scaled logit) or variations in rounding strategies (e.g., three-class rounding). The core innovation of SGA+ likely lies in the improved optimization of the latent variables, leading to superior compression efficiency compared to the original SGA and other baseline methods. A key aspect of the evaluation would likely be the demonstration of improved rate-distortion trade-offs on standard image compression benchmarks, showcasing reduced bitrates for comparable image quality or improved image quality at similar bitrates. Further, it would focus on showing that SGA+ is less sensitive to hyperparameter tuning, hence providing a more robust solution to latent refinement in the context of neural image compression.
Three-Class Rounding#
The proposed three-class rounding method extends the typical two-class (floor/ceiling) approach in latent optimization for neural image compression. Instead of simply rounding to the nearest integer, it introduces the possibility of rounding to a value one step further away. This is achieved by extending existing functions used in SGA+, like linear, cosine, and Sigmoid Scaled Logit (SSL), to handle three possible outcomes. The main motivation is to improve the optimization process by enabling smoother transitions in the probability space, particularly at the boundaries, thereby reducing the likelihood of gradient saturation and allowing for better handling of the discretization gap. The extension to three classes provides an interpolation between the floor and ceiling operations, leading to improved results on standard compression datasets like Kodak, Tecnick and CLIC. This flexibility offers a balance between the computational overhead of three-class rounding and the potential performance gains, particularly useful when optimizing for specific rate-distortion trade-offs. Overall, the results demonstrate that three-class rounding can be a beneficial modification to latent optimization techniques, potentially improving the efficiency and the convergence behavior of compression models. However, it necessitates careful hyperparameter tuning (like scaling factor ‘r’ and power ’n’) to avoid suboptimal convergence or gradient instability.
Compression Gains#
Analyzing compression gains requires a multifaceted approach. Quantifying the improvements is crucial, often measured by metrics like bits per pixel (BPP) reduction or peak signal-to-noise ratio (PSNR) increase. Understanding the trade-off between rate and distortion is vital; higher compression (lower BPP) usually comes at the cost of some image quality degradation (lower PSNR). The context of the gains is critical—are they absolute or relative to existing methods? How do they perform across different datasets or image types? Generalizability is key: gains observed in limited scenarios might not hold up universally. Finally, the methodology used to achieve the gains is important. Are they the product of sophisticated new algorithms, or simpler modifications to existing techniques? The insights from this analysis ultimately shape our understanding of the value and practicality of any compression advancements.
Future Research#
Future research directions stemming from this work could explore several avenues. Extending SGA+ to handle even more complex data modalities such as video or 3D point clouds would be a significant advancement. Investigating alternative probability space functions beyond the linear, cosine, and sigmoid scaled logit, could potentially lead to even better compression performance and reduced sensitivity to hyperparameters. A deeper theoretical analysis of the relationship between the chosen probability function, the gradient characteristics, and the resulting R-D performance would solidify the understanding of the underlying mechanisms. Furthermore, exploring different quantization strategies that go beyond two-class or three-class rounding, such as learned or adaptive quantization schemes, could further improve compression efficiency. Finally, it would be important to evaluate the trade-offs between computational cost and performance enhancements of different SGA+ methods to optimize practical applications.
More visual insights#
More on figures
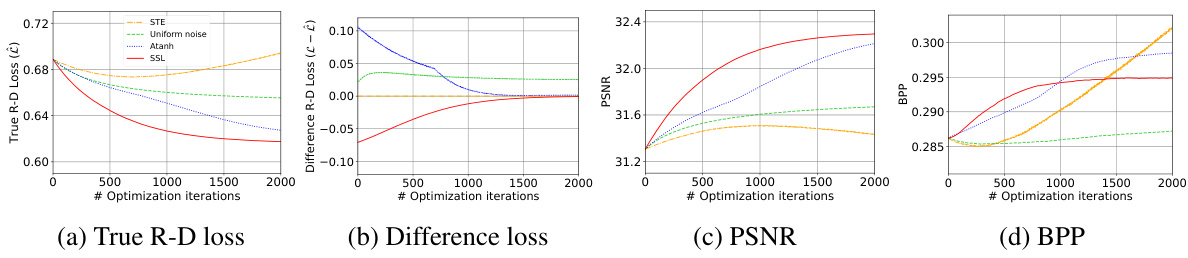
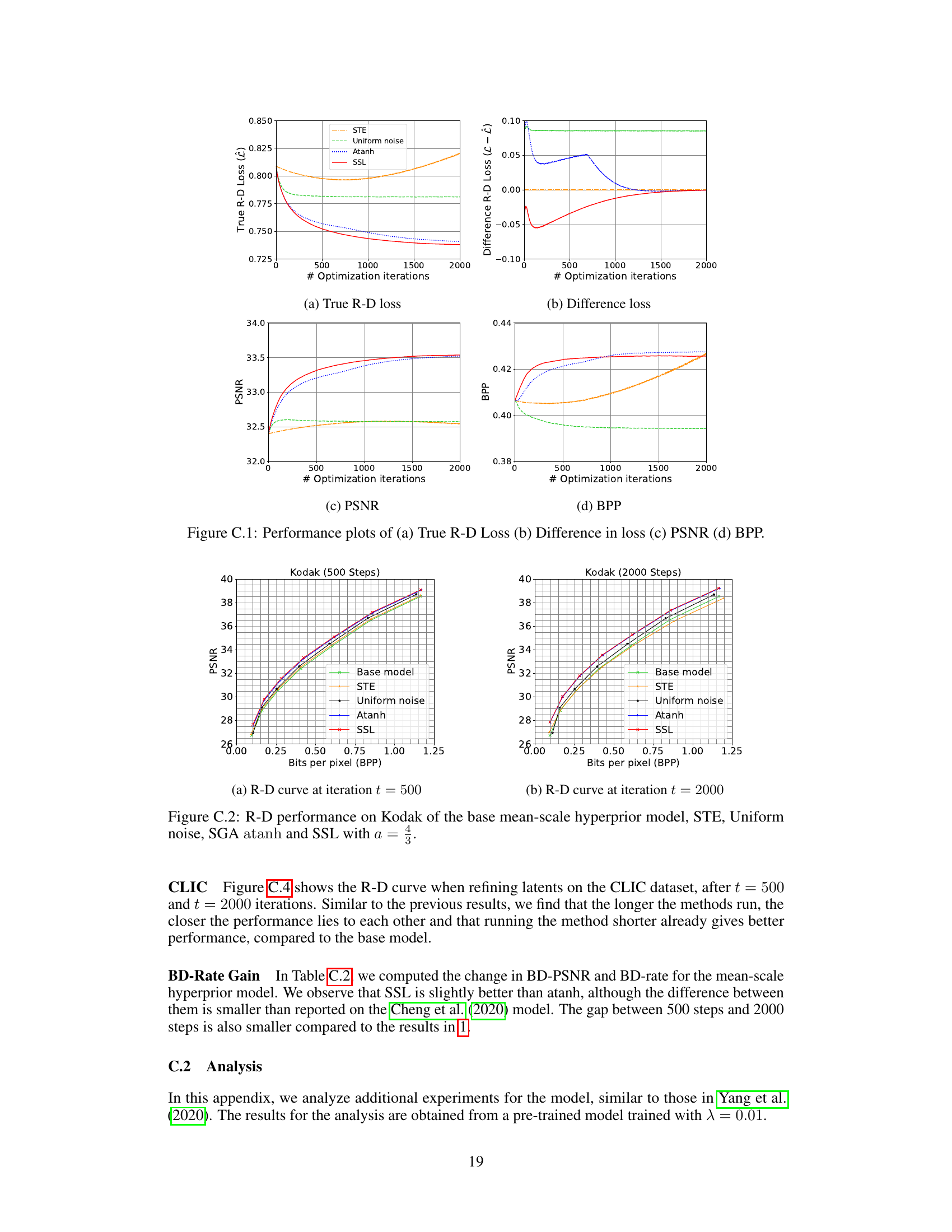
🔼 This figure shows the performance of different methods for refining latents in neural image compression. (a) displays the true rate-distortion loss, which measures the trade-off between compression rate and reconstruction quality. (b) shows the difference between the method’s loss and the true loss, highlighting the accuracy of the method’s loss estimation. (c) and (d) illustrate the peak signal-to-noise ratio (PSNR) and bits per pixel (BPP), respectively, which are common metrics for evaluating image quality and compression efficiency. The plots reveal that SSL converges more smoothly and achieves a lower true R-D loss compared to other methods, suggesting superior performance in refining latents for image compression.
read the caption
Figure 2: Performance plots of (a) True R-D Loss (b) Difference in loss (c) PSNR (d) BPP.

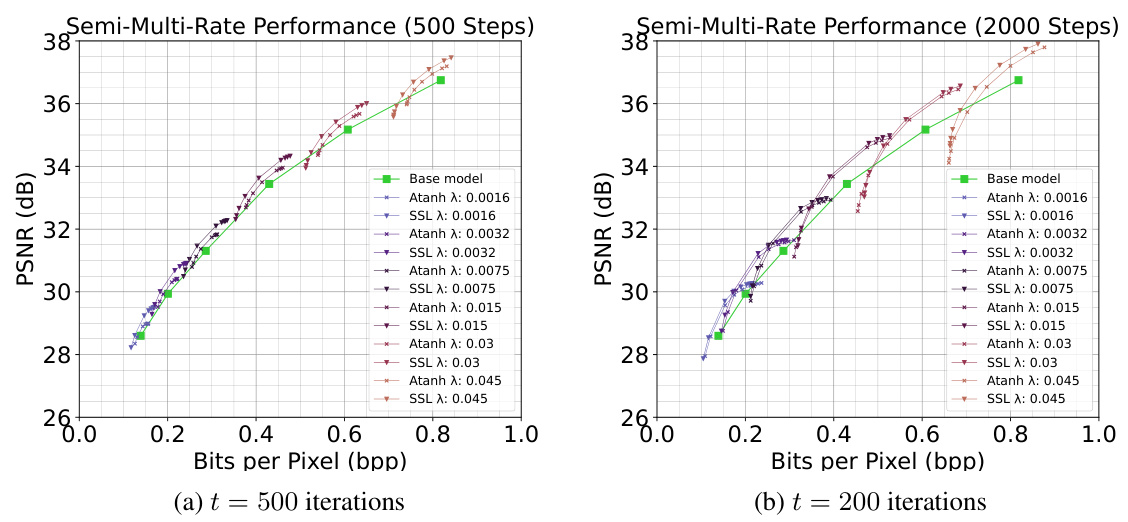
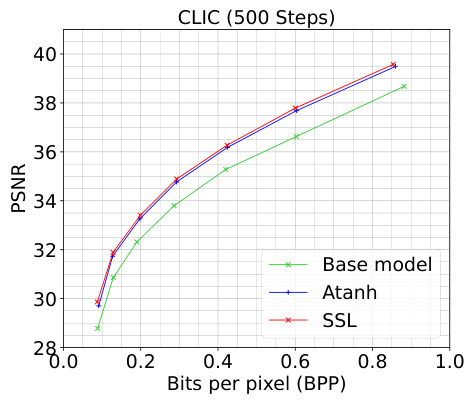
🔼 This figure presents the rate-distortion performance of the proposed SSL method compared to baselines (STE, uniform noise, atanh) across three scenarios. (a) shows the comparison on the Kodak dataset, highlighting SSL’s superior performance. (b) demonstrates the comparison on the Tecnick dataset, again showing SSL’s advantage. (c) illustrates the semi-multi-rate behavior of SSL on Kodak, demonstrating its flexibility in adapting to different compression targets.
read the caption
Figure 3: R-D performance for SSL on (a) Kodak with the baselines, (b) Tecnick with the base model and atanh and (c) Kodak for semi-multi-rate behavior with atanh. Best viewed electronically.

🔼 This figure presents a qualitative comparison of the visual results obtained from the proposed method (SSL) against its predecessors. The original image and its compressed versions using a basic model, atanh, and SSL are shown. The comparison focuses on visual quality to highlight the improvements achieved in reducing artifacts with SSL. The BPP (bits per pixel) and PSNR (peak signal-to-noise ratio) values are also provided for each method to quantify the compression performance.
read the caption
Figure 4: Qualitative comparison of a Kodak image from pre-trained model trained with λ = 0.0016. Best viewed electronically.

🔼 This figure visualizes the probability space for different methods used in the paper for two-class and three-class rounding. Panel (a) shows the probability of flooring ([v]) and ceiling ([v]) for various methods like atanh, linear, cosine, and sigmoid scaled logit (SSL) as a function of the input variable v. The curves illustrate the smoothness and gradient behavior of each method. Panel (b) extends this visualization to three-class rounding, showing the probabilities of rounding to [v]-1, [v], and [v]+1 using a modified linear function. This helps compare the differences in probability distributions and potential gradient issues for each method.
read the caption
Figure 1: Probability space for (a) Two-class rounding (b) Three-class rounding

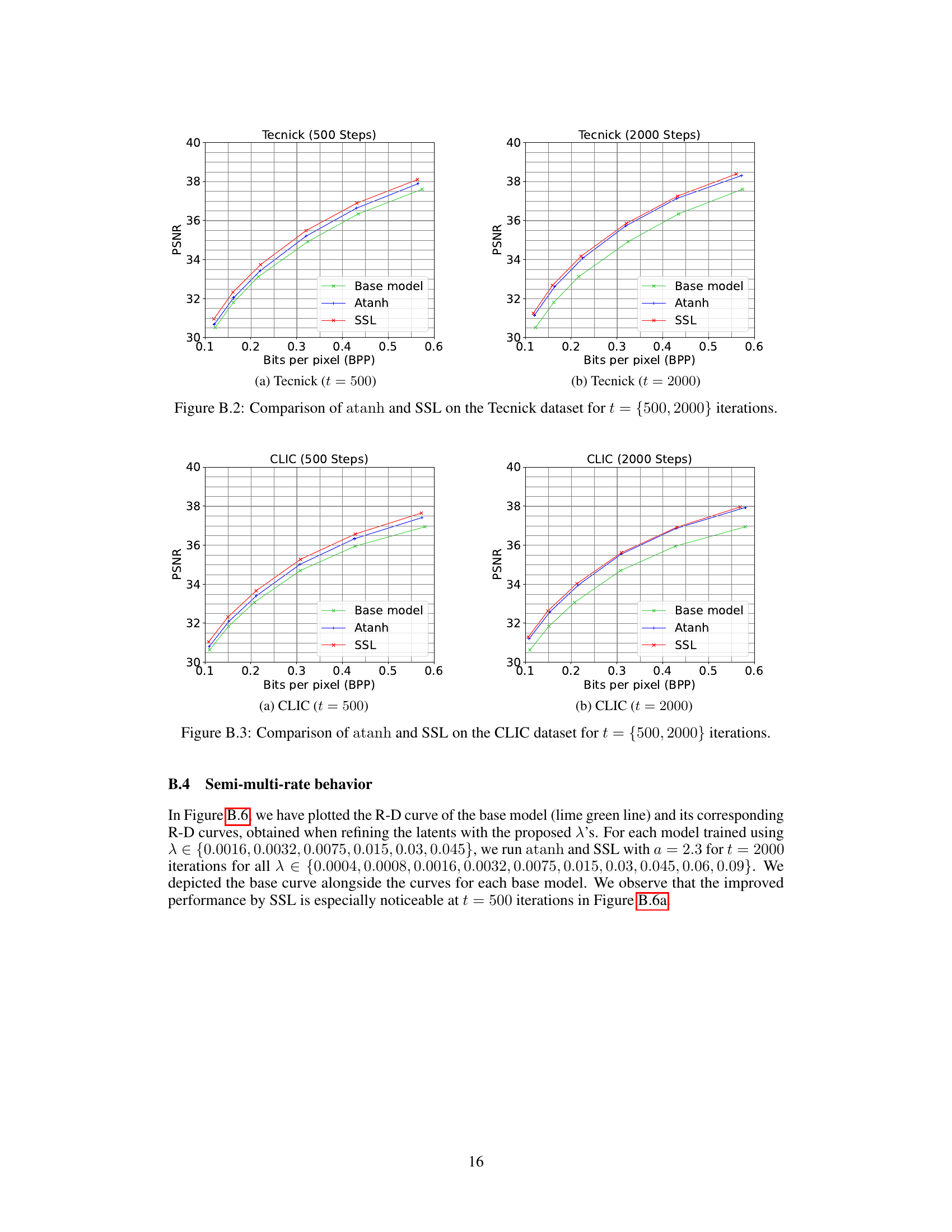
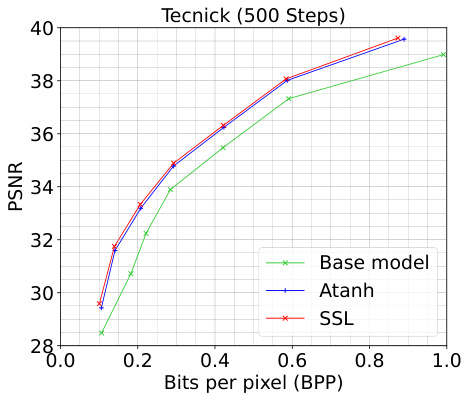
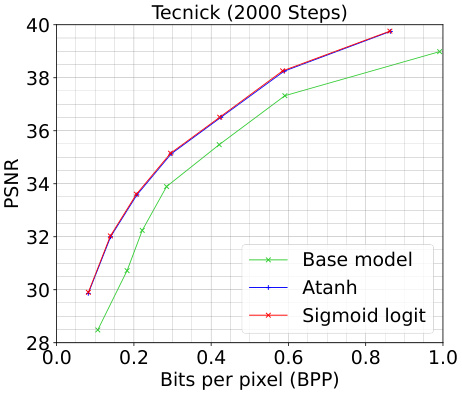
🔼 This figure compares the rate-distortion performance of the atanh and SSL methods against a baseline model on the Tecnick dataset. Two plots are presented, one for 500 iterations of refinement and one for 2000 iterations. The plots show the peak signal-to-noise ratio (PSNR) versus bits per pixel (BPP), illustrating the trade-off between image quality and compression rate. The results demonstrate how the SSL method improves compression performance compared to atanh, especially at 2000 iterations.
read the caption
Figure B.2: Comparison of atanh and SSL on the Tecnick dataset for t = {500, 2000} iterations.
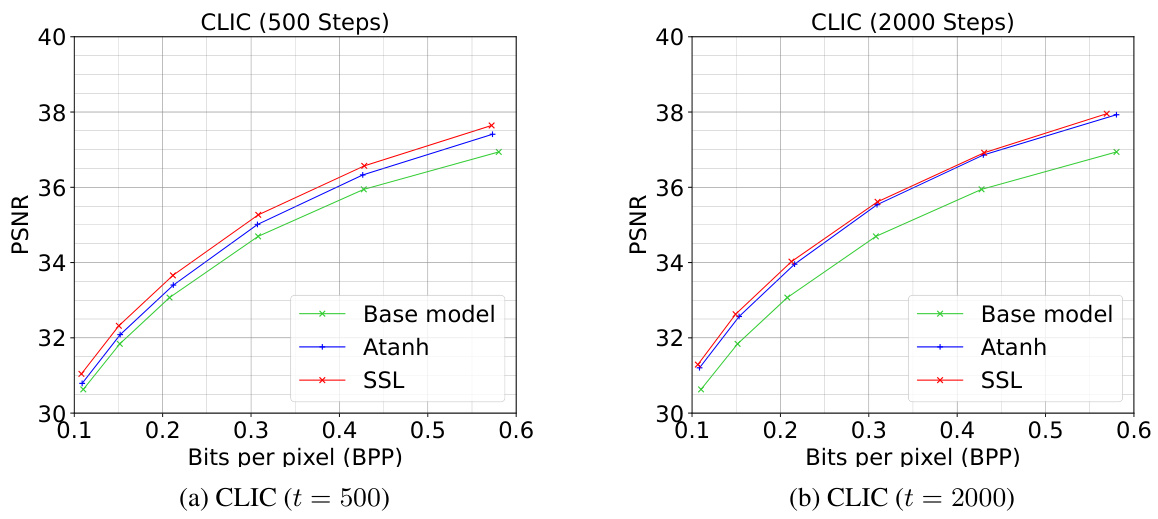
🔼 This figure shows three plots that illustrate the rate-distortion performance of the proposed method (SSL) in comparison to several baselines. Plot (a) shows the performance on the Kodak dataset where SSL achieves the best performance compared to others. Plot (b) shows the same performance but this time on Tecnick dataset. Plot (c) shows the semi-multi-rate performance. For each model trained using λ∈{0.0016, 0.0032, 0.0075, 0.015, 0.03, 0.045}, the refinement is run for 500 iterations.
read the caption
Figure 3: R-D performance for SSL on (a) Kodak with the baselines, (b) Tecnick with the base model and atanh and (c) Kodak for semi-multi-rate behavior with atanh. Best viewed electronically.

🔼 This figure shows the probability space of different methods used for rounding, including atanh, linear, cosine, and sigmoid scaled logit (SSL). Panel (a) illustrates the two-class rounding scenario, visualizing the probabilities of flooring and ceiling for each method. The figure highlights the differences in gradient behavior and probability distribution between these methods, particularly emphasizing the problems of gradients tending to infinity for atanh near the boundaries of 0 and 1. Panel (b) extends this visualization to show three-class rounding for the linear method, comparing the two-class with the three-class case in terms of smoothness and rounding probabilities. This visual comparison helps to understand how the proposed methods of SGA+ aim to overcome the limitations of existing methods, especially the problematic behavior of atanh, by providing more stable gradients during optimization.
read the caption
Figure 1: Probability space for (a) Two-class rounding (b) Three-class rounding

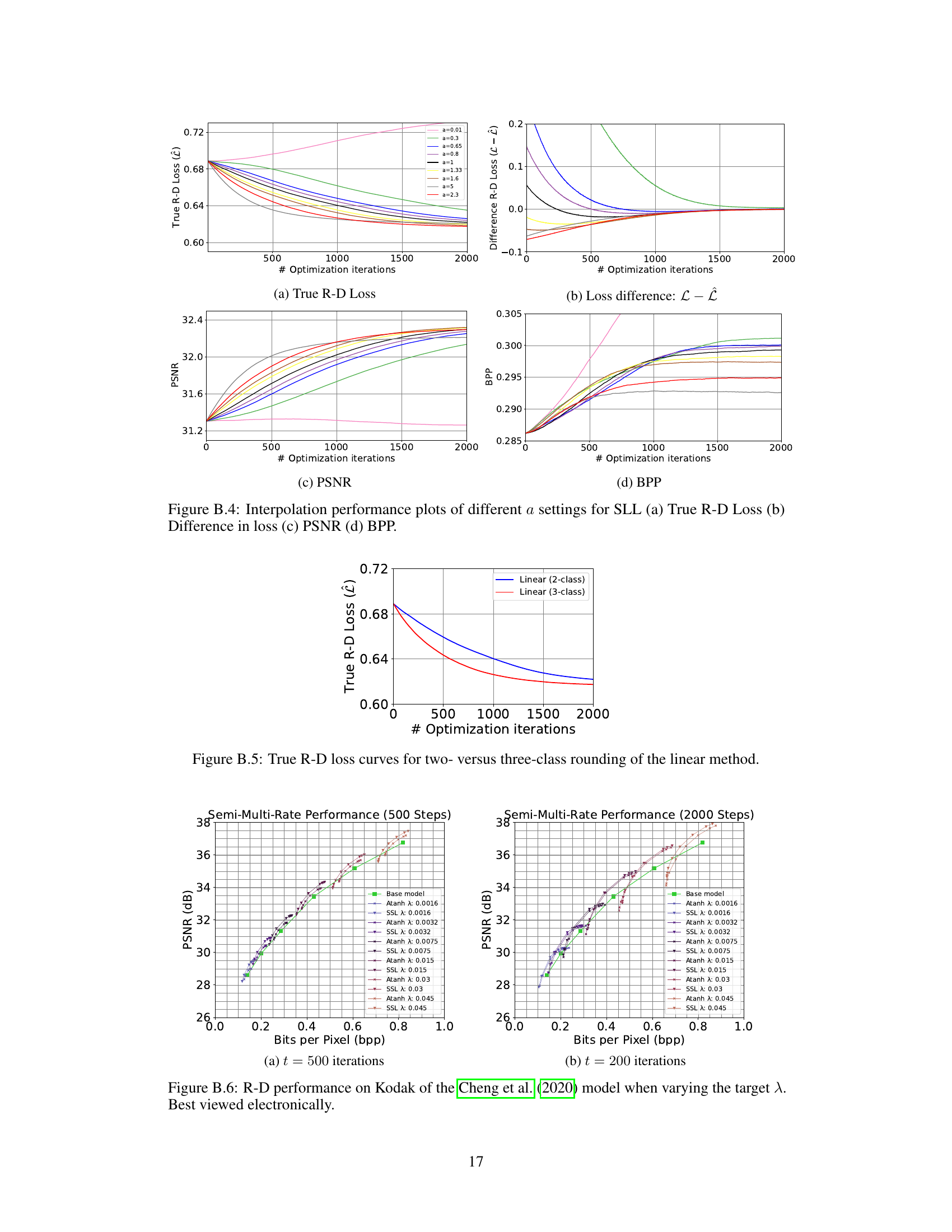
🔼 This figure compares the true rate-distortion loss curves for two-class and three-class rounding using the linear probability method from the proposed SGA+ algorithm. It shows that the three-class rounding converges faster to a lower loss than the two-class rounding, especially in the initial stages of optimization. This highlights a potential advantage of the three-class approach in terms of faster convergence and potentially lower final loss.
read the caption
Figure B.5: True R-D loss curves for two- versus three-class rounding of the linear method.
🔼 The figure illustrates the probability space for different methods used for two-class and three-class rounding in the context of latent optimization for neural image compression. Panel (a) shows the probability space for various methods including atanh, linear, cosine, and sigmoid scaled logit (SSL) for two-class rounding. Panel (b) presents the extended version of the linear method for three-class rounding, highlighting the effect of the number of classes and smoothness on the probability space. These probability spaces are crucial for understanding the behavior of different rounding methods during latent optimization, impacting the compression performance and sensitivity to hyperparameter choices.
read the caption
Figure 1: Probability space for (a) Two-class rounding (b) Three-class rounding
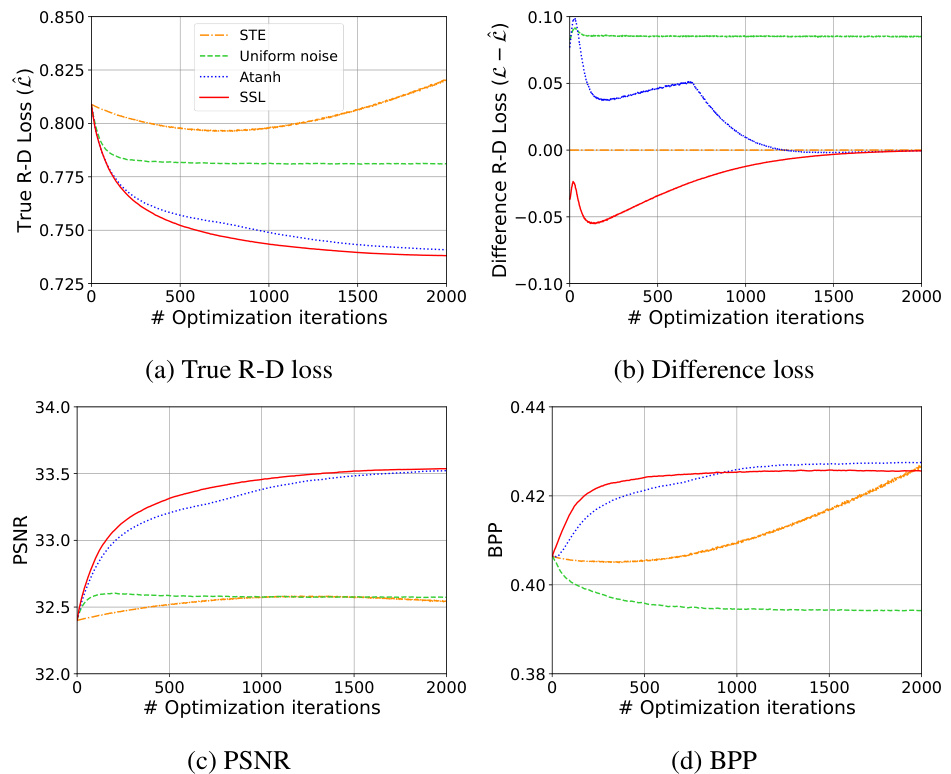
🔼 This figure presents the performance plots of four different methods: STE, Uniform noise, atanh, and SSL. The plots show the true rate-distortion loss, the difference between the method loss and true loss, the peak signal-to-noise ratio (PSNR), and the bits per pixel (BPP). These metrics are used to evaluate the effectiveness of each method in optimizing the latent variables for neural image compression. Each method shows how it converges over 2000 iterations.
read the caption
Figure 2: Performance plots of (a) True R-D Loss (b) Difference in loss (c) PSNR (d) BPP.
🔼 The figure shows a comparison of the probability spaces of different methods for two-class and three-class rounding. Panel (a) compares the atanh function used in the original SGA method with the linear, cosine, and sigmoid scaled logit (SSL) functions proposed in the SGA+ method. The solid lines represent the probability of flooring ([v]), while the dotted lines represent the probability of ceiling ([v]). Panel (b) illustrates the three-class rounding extension of the linear function, showing the probabilities of rounding to [v]-1, [v], and [v]+1. The figure highlights how the proposed methods in SGA+ offer smoother probabilities and potentially better gradient characteristics compared to the atanh function, thus improving the optimization of latents during the refinement process.
read the caption
Figure 1: Probability space for (a) Two-class rounding (b) Three-class rounding
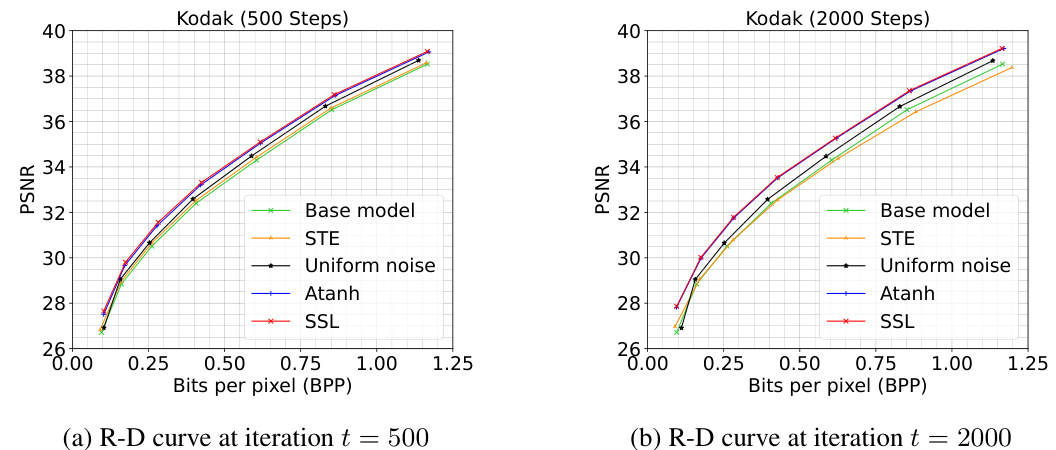
🔼 This figure compares the Rate-Distortion performance of the proposed SSL method against atanh for the Tecnick dataset. Two sets of curves are shown, one for 500 optimization iterations and one for 2000. The plots show the peak signal-to-noise ratio (PSNR) against bits per pixel (BPP), illustrating the trade-off between image quality and compression rate. The figure demonstrates that SSL generally outperforms atanh in terms of achieving higher PSNR for a given BPP, indicating superior compression performance. The improvement is more noticeable at 2000 iterations.
read the caption
Figure B.2: Comparison of atanh and SSL on the Tecnick dataset for t = {500, 2000} iterations.
🔼 This figure compares the rate-distortion performance of atanh and SSL on the Tecnick dataset for two different numbers of optimization iterations (500 and 2000). The plot shows the PSNR (Peak Signal-to-Noise Ratio) which is a measure of image quality against the bits per pixel (BPP) which represents the compression rate. It demonstrates how the refinement of latents using SSL improves compression performance, especially at 2000 iterations, when compared to atanh and the base model.
read the caption
Figure B.2: Comparison of atanh and SSL on the Tecnick dataset for t = {500, 2000} iterations.
🔼 This figure presents a comparison of the Rate-Distortion performance between atanh and SSL methods on the Kodak dataset for two different numbers of optimization iterations: 500 and 2000. The plot shows PSNR (Peak Signal-to-Noise Ratio) on the y-axis and Bits Per Pixel (BPP) on the x-axis. It visually demonstrates how the performance of SSL changes over the different number of iterations, and also allows for a comparison against the performance of the atanh method and a baseline model.
read the caption
Figure B.1: Comparison of atanh and SSL on the Kodak dataset for t = {500, 2000} iterations.

🔼 This figure shows three rate-distortion (R-D) curves. The first shows the performance of SSL on the Kodak dataset compared to baselines (STE, Uniform noise, and atanh). The second shows SSL performance on the Tecnick dataset compared to atanh and the base model. The third demonstrates the semi-multi-rate behavior of SSL on the Kodak dataset compared to atanh. The plots illustrate the peak signal-to-noise ratio (PSNR) versus bits per pixel (BPP), highlighting the compression performance of different methods.
read the caption
Figure 3: R-D performance for SSL on (a) Kodak with the baselines, (b) Tecnick with the base model and atanh and (c) Kodak for semi-multi-rate behavior with atanh. Best viewed electronically.

🔼 This figure shows three plots. Plot (a) presents the rate-distortion (R-D) performance for different methods on the Kodak dataset. Plot (b) shows the R-D curves on the Tecnick dataset. Plot (c) illustrates semi-multi-rate behavior for the Kodak dataset. The plots compare the performance of the proposed SSL method against baselines such as atanh and uniform noise. In each plot, the x-axis represents bits per pixel (BPP), and the y-axis represents peak signal-to-noise ratio (PSNR).
read the caption
Figure 3: R-D performance for SSL on (a) Kodak with the baselines, (b) Tecnick with the base model and atanh and (c) Kodak for semi-multi-rate behavior with atanh. Best viewed electronically.

🔼 This figure shows a comparison of the rate-distortion performance of the proposed SSL method against several baselines. Panel (a) shows the results for the Kodak dataset; Panel (b) displays the results for the Tecnick dataset; Panel (c) illustrates the semi-multi-rate behavior on Kodak. The plots show PSNR (peak signal-to-noise ratio) versus bits per pixel (bpp), illustrating the trade-off between image quality and compression size. The SSL method generally outperforms other methods in terms of achieving higher PSNR for a given bpp.
read the caption
Figure 3: R-D performance for SSL on (a) Kodak with the baselines, (b) Tecnick with the base model and atanh and (c) Kodak for semi-multi-rate behavior with atanh. Best viewed electronically.

🔼 The figure shows the true rate-distortion loss curves for different learning rates (0.005, 0.01, and 0.02) for both SSL and atanh methods. It demonstrates the convergence behavior of each method at different learning rates over 2000 optimization iterations. The plot allows for a comparison of stability and convergence speed across various learning rate settings and methods.
read the caption
Figure C.6: True R-D loss curves for different learning rates settings for method SSL and atanh.
🔼 This figure shows the probability space for several methods proposed in the paper for two-class rounding (left) and three-class rounding (right). The left plot visualizes how different functions (atanh, linear, cosine, and sigmoid scaled logit (SSL) with different parameters) map the continuous variable v to probabilities of rounding down or up, illustrating their characteristics. The right plot extends this to three classes, showing how probabilities for rounding to [v]-1, [v], and [v]+1 are defined using the linear function. The plots highlight the differences in gradient behavior and smoothness across the various methods, which affect the efficiency of optimization and overall performance.
read the caption
Figure 1: Probability space for (a) Two-class rounding (b) Three-class rounding
More on tables
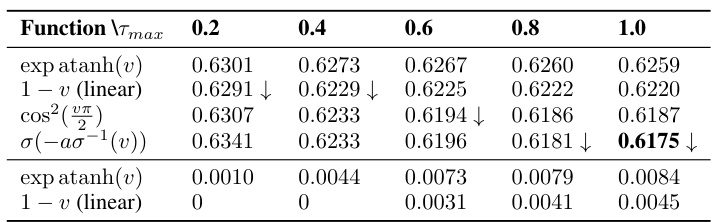
🔼 This table presents the true rate-distortion loss for different temperature settings (Tmax) using four different methods for calculating the unnormalized log probabilities: atanh, linear, cosine, and sigmoid scaled logit (SSL). The lowest R-D loss for each Tmax value is marked. The atanh function is noted as unnormalized.
read the caption
Table 2: True R-D loss for different Tmax settings of: atanh(v), linear, cosine and SSL with a = 2.3. The lowest R-D loss per column is marked with: ↓. Note that the function containing atanh is unnormalized.

🔼 This table presents a pairwise comparison of the BD-PSNR (Bjontegaard Delta Peak Signal-to-Noise Ratio) and BD-Rate (Bjontegaard Delta Rate) between the atanh (inverse hyperbolic tangent) and SSL (Sigmoid Scaled Logit) methods. The comparison is shown for three datasets: Kodak, Tecnick, and CLIC, and for two different numbers of optimization iterations: 500 and 2000. The BD-PSNR values represent the difference in PSNR between the two methods, indicating improvement in image quality. The BD-Rate values show the difference in bitrate, reflecting the change in compression efficiency. Positive BD-PSNR values indicate an improvement in PSNR by SSL over atanh, and negative BD-Rate values indicate an improvement in compression rate by SSL over atanh.
read the caption
Table 1: Pairwise Comparison between atanh and SSL of BD-PSNR and BD-Rate.

🔼 This table shows the true rate-distortion loss for different values of the hyperparameter ‘a’ in the Sigmoid Scaled Logit (SSL) function. The values of ‘a’ are chosen to show how the function interpolates between different probability functions: atanh, linear, and cosine. The lowest R-D loss, indicating the best performance, is marked with a down arrow.
read the caption
Table 4: True R-D loss results for the interpolation between different functions by changing a of the SSL.

🔼 This table shows the true rate-distortion loss for different settings of the sigmoid scaled logit (SSL) function. The values of ‘a’ represent different shapes of the function, interpolating between linear, cosine, and atanh functions. The lowest R-D loss is marked with a down arrow. This table helps to analyze how sensitive the SSL function is to the hyperparameter ‘a’ and find the optimal value for the best compression performance.
read the caption
Table C.1: True R-D loss results for the interpolation between different functions by changing a of the SSL.

🔼 This table presents a pairwise comparison of the BD-PSNR (Bjontegaard Delta Peak Signal-to-Noise Ratio) and BD-Rate (Bjontegaard Delta Rate) between the atanh and SSL methods. The BD-PSNR indicates the improvement in image quality, while the BD-Rate reflects the improvement in compression efficiency. Results are shown for 500 and 2000 optimization steps, across three datasets: Kodak, Tecnick, and CLIC. The table allows for a direct comparison of the two methods’ performance across different datasets and optimization lengths.
read the caption
Table 1: Pairwise Comparison between atanh and SSL of BD-PSNR and BD-Rate.

🔼 This table shows the true rate-distortion loss for different learning rates (0.02, 0.01, and 0.005) for both atanh and SSL methods using a fixed α of 2.3. The results are presented for both 500 and 2000 iterations, showing the convergence over time. This helps to analyze the impact of the learning rate on the performance and stability of the methods.
read the caption
Table C.3: True R-D loss for different learning settings of: atanh and SSL with α = 2.3. At t = 2000 iterations and in brackets t = 500 iterations

🔼 This table presents the true rate-distortion loss for different maximum temperature settings (Tmax) using four different functions: atanh, linear, cosine, and sigmoid scaled logit (SSL) with a = 2.3. The lowest R-D loss for each Tmax value is marked. Note that the atanh function is not normalized.
read the caption
Table 2: True R-D loss for different Tmax settings of: atanh(v), linear, cosine and SSL with a = 2.3. The lowest R-D loss per column is marked with: ↓. Note that the function containing atanh is unnormalized.
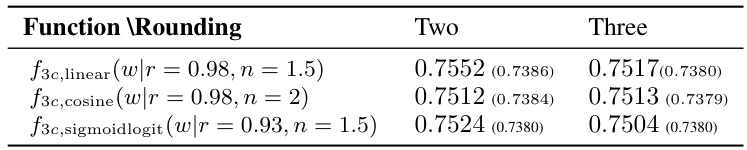
🔼 This table presents the true rate-distortion loss for two different rounding methods (two-class and three-class) applied to three functions (linear, cosine, and sigmoid scaled logit) used within the Stochastic Gradient Gumbel Annealing+ (SGA+) algorithm. Results are shown for both 500 and 2000 iterations of the algorithm, indicating the trade-off between rate and distortion at different stages of the optimization process. The values allow comparison of the effect of increasing the number of rounding classes (from two to three) on the compression performance achieved by the different functions within SGA+.
read the caption
Table C.5: True R-D loss of two versus three-class rounding for SGA+ with the extended version of the linear, cosine, and SSL method at iteration 500 and in brackets after 2000 iterations.
Full paper#