TL;DR#
Binocular 3D human pose estimation offers advantages over monocular methods by using multiple views to reduce depth ambiguity. However, it still suffers from higher uncertainties compared to multi-view setups due to fewer cameras. Existing methods often rely on explicit pose priors or complex network architectures, or tackle uncertainty issues using limited statistical models. These approaches either lack flexibility or efficiency.
This paper introduces Dual-Diffusion, a novel method specifically designed for binocular 3D HPE that addresses these challenges. It leverages a diffusion model to simultaneously denoise initial 2D and 3D pose uncertainties by using geometric mapping to connect the two domains. It also introduces Z-embedding and baseline-width-related pose normalization to improve the flexibility of the model. Extensive experiments demonstrate that Dual-Diffusion achieves superior performance compared to existing methods.
Key Takeaways#
Why does it matter?#
This paper is important because it presents Dual-Diffusion, a novel framework for binocular 3D human pose estimation that significantly improves accuracy and robustness. It addresses the limitations of existing methods by simultaneously denoising 2D and 3D uncertainties, leveraging the strengths of binocular vision while mitigating its challenges. This work opens new avenues for research in 3D human pose estimation and related fields, particularly in improving the accuracy and reliability of pose estimation in scenarios with limited camera viewpoints.
Visual Insights#
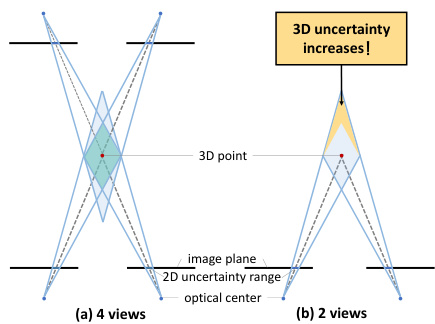
🔼 This figure compares the uncertainty of 3D point reconstruction using binocular and multi-view setups. The left panel (a) shows a 3D point reconstructed from four views, demonstrating low 3D uncertainty due to multiple observations. The right panel (b) shows a 3D point reconstructed from just two views, resulting in a significantly larger 3D uncertainty range. The increased uncertainty highlights the challenge of binocular 3D human pose estimation where the number of views is limited, compared to multi-view approaches.
read the caption
Figure 1: Binocular reconstruction has higher 3D uncertainty compared to multi-view configurations.
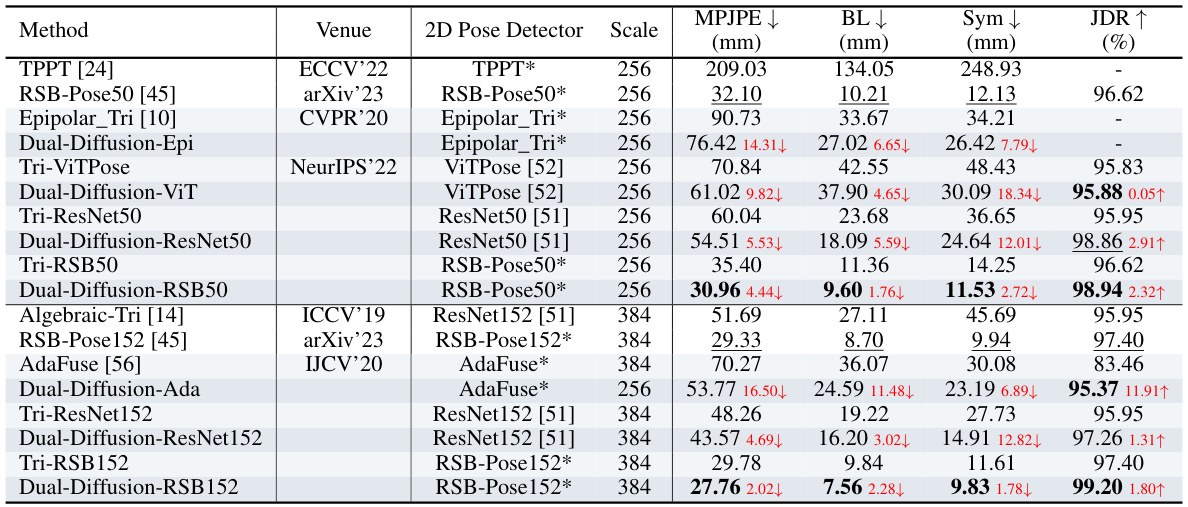
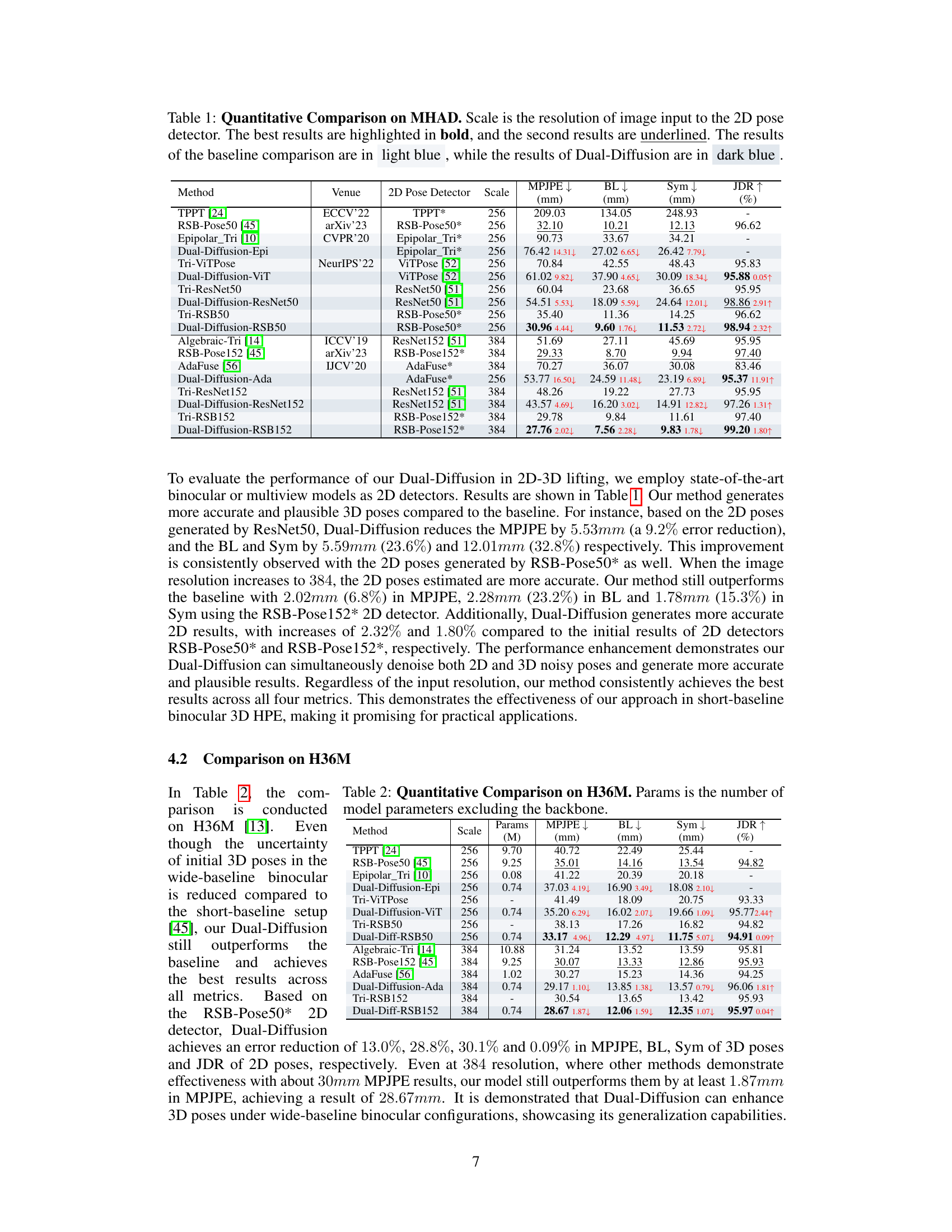
🔼 This table presents a quantitative comparison of different methods for 3D human pose estimation on the MHAD dataset. It compares the performance of Dual-Diffusion against several baselines and state-of-the-art methods using different 2D pose detectors and image resolutions. Metrics include Mean Per Joint Position Error (MPJPE), Bone Length error (BL), Symmetry error (Sym), and Joint Detection Rate (JDR). The best and second-best results for each metric are highlighted to show the superior performance of the proposed Dual-Diffusion method.
read the caption
Table 1: Quantitative Comparison on MHAD. Scale is the resolution of image input to the 2D pose detector. The best results are highlighted in bold, and the second results are underlined. The results of the baseline comparison are in light blue, while the results of Dual-Diffusion are in dark blue.
In-depth insights#
Dual Diffusion HPE#
Dual Diffusion for binocular 3D Human Pose Estimation offers a novel approach to address the inherent uncertainties in reconstructing 3D poses from binocular 2D data. The core innovation lies in its simultaneous denoising of both 2D and 3D data, leveraging the power of diffusion models. Unlike monocular approaches, it recognizes the intrinsic link between 2D and 3D uncertainties in a binocular setup and utilizes this relationship to improve accuracy. The method elegantly incorporates geometric constraints through triangulation and reprojection, thereby refining both 2D and 3D estimations iteratively. Z-embedding and baseline-width-related pose normalization further enhance the model’s flexibility and adaptability to diverse settings. The framework cleverly addresses the unknown distribution of 3D pose uncertainty by directly using well-defined 2D uncertainty as a starting point, making it more robust and practical than statistical methods.
Uncertainty Modeling#
The concept of ‘Uncertainty Modeling’ in the context of binocular 3D human pose estimation is crucial because of the inherent ambiguities in reconstructing 3D poses from 2D observations. The paper likely explores how uncertainties in the initial 2D pose estimations propagate to the 3D pose estimates, emphasizing the challenges introduced by the reduced number of cameras compared to multi-view setups. A key aspect would be the modeling of the 2D uncertainty, perhaps using a Gaussian distribution centered at the detected 2D joint locations. The paper then likely proposes a method to leverage this 2D uncertainty information to refine or denoise the initial 3D poses obtained through triangulation or another method. This involves understanding the relationship between 2D and 3D uncertainties, which is non-trivial due to the geometric constraints and depth ambiguity in binocular vision. The core of the uncertainty modeling may involve a diffusion model, which probabilistically refines the 3D pose estimates, effectively learning to reduce uncertainty while maintaining geometric consistency. This approach might involve simultaneously denoising 2D and 3D data, propagating information between the two domains, and making use of human pose priors. The success of such a model would depend heavily on the ability to accurately capture and model the complex interactions and propagation of uncertainties in a binocular setup, potentially incorporating depth information and baseline width to better capture the 3D uncertainty distribution.
Binocular 3D HPE#
Binocular 3D Human Pose Estimation (HPE) presents a compelling alternative to monocular and multiview approaches. It leverages the strengths of both: the convenience of a monocular setup with the improved 3D accuracy afforded by multiple viewpoints (albeit only two). The challenge lies in mitigating the increased uncertainty inherent in binocular reconstruction compared to systems using more cameras. Existing methods often struggle with this ambiguity, relying on explicit pose priors or computationally expensive techniques. This paper proposes a novel solution to effectively reconstruct 3D poses by using a diffusion model which is particularly suitable for handling the inherently uncertain nature of the 2D inputs. This approach shows potential for robustly denoising both 2D and 3D estimations simultaneously, leading to significantly improved accuracy and plausibility in 3D pose reconstruction. The key novelty lies in cleverly using the well-defined uncertainty of the initial 2D poses to inform the denoising process of the less well-defined 3D poses, creating a more efficient and accurate method for binocular 3D HPE.
Denoiser Enhancements#
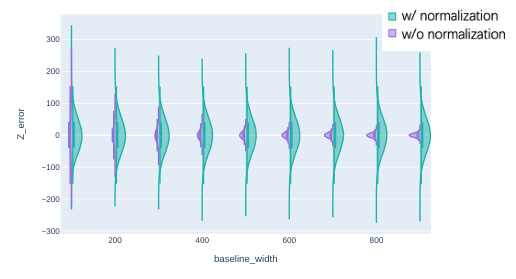
Denoiser enhancements in this context likely involve techniques to improve the performance and robustness of the denoising process within a diffusion model for 3D human pose estimation. This might include strategies to better handle uncertainty, such as incorporating depth information (z-embedding) or normalizing for varying baselines (baseline-width normalization). The goal is to refine the initial noisy 3D pose estimates by leveraging the inherent relationship between 2D and 3D uncertainties. This could involve clever use of geometric constraints or other pose priors, enhancing the denoiser’s ability to disambiguate between plausible and implausible poses, improving the accuracy of the final 3D pose reconstruction. Z-embedding, for example, could act as a conditioning variable to guide the denoising process based on depth information, enabling more accurate depth recovery. Baseline-width normalization could make the model more flexible and less sensitive to different camera configurations, which is crucial as baseline width influences the 3D error. Overall, these enhancements aim for more accurate and robust pose estimation even when dealing with initial noisy data and varying factors such as baseline distances.
Future of DD-HPE#
The future of Dual-Diffusion Human Pose Estimation (DD-HPE) is promising, with potential advancements focusing on enhanced robustness, increased efficiency, and broader applications. Improving robustness could involve exploring more sophisticated noise models within the diffusion process, handling occlusions more effectively, and incorporating advanced regularization techniques. Efficiency gains might be achieved through architectural optimizations of the denoising network, leveraging more efficient diffusion schedules, or exploring alternative training strategies. Expanding applicability could encompass extending DD-HPE to more challenging scenarios, such as low-light conditions, complex backgrounds, or diverse viewpoints. Furthermore, integration with other computer vision tasks, such as action recognition and human-robot interaction, is highly promising. Addressing the limitations related to depth ambiguity and baseline width dependency, as noted in the paper, will be crucial for advancing the accuracy and generalizability of DD-HPE. Finally, exploration of novel diffusion model architectures and the incorporation of advanced prior knowledge about human pose and movement dynamics offers significant potential for further progress in this exciting area of research.
More visual insights#
More on figures
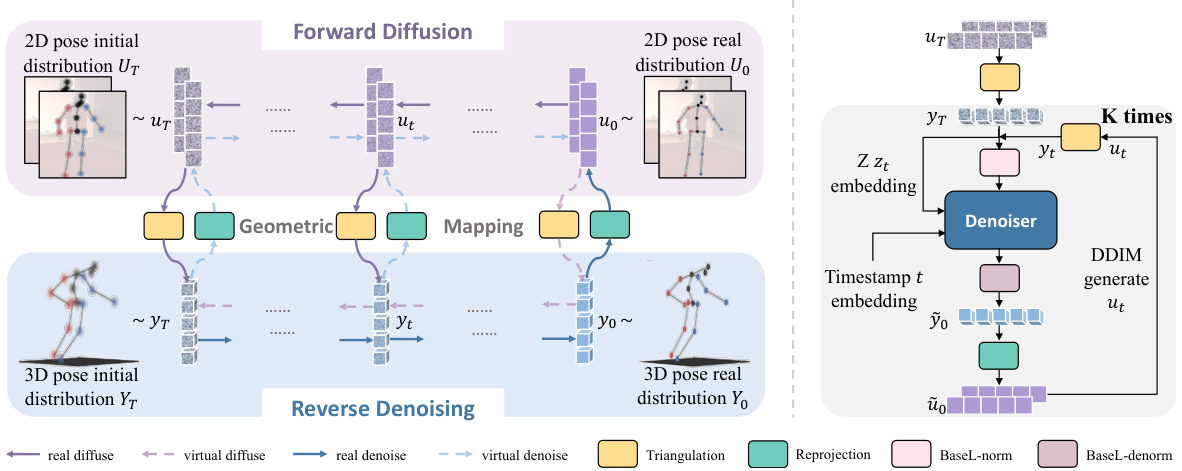
🔼 This figure illustrates the Dual-Diffusion method proposed in the paper. Panel (a) shows the modeling process: Noise is added iteratively to the ground truth 2D poses in the forward diffusion. These noisy 2D poses are then used to estimate noisy 3D poses via triangulation. The reverse denoising process then refines these noisy 3D poses to obtain accurate 3D poses, which are then reprojected back to 2D space for consistency checking. Panel (b) depicts the inference process: Noisy 2D poses are used as input, converted to initial 3D poses, and then refined iteratively through K denoising steps, resulting in refined 3D poses and corresponding 2D poses.
read the caption
Figure 2: Overview of Dual-Diffusion Method. (a) Modeling: In the forward diffusion process, noise is added to the ground truth binocular 2D poses uT for T steps, aligning with the distribution of initial estimated 2D poses. During the reverse denoising process, noisy 3D poses are progressively denoised to plausible poses. Geometric mapping is employed to connect 2D and 3D domains. (b) Inference: The initial 3D pose yT, reconstructed from binocular 2D poses uT, is denoised to y0. Then y0 is reprojected to the denoised 2D poses u0. The entire denoising process iterates for K times.
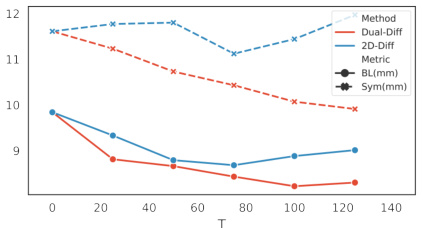
🔼 This figure shows the comparison of Dual-Diff and 2D-Diff methods under different diffusion steps (T). The plot displays the Bone Length error (BL) and Symmetry error (Sym) for both methods as T varies. The results indicate that Dual-Diff consistently outperforms 2D-Diff across all values of T, highlighting the effectiveness of denoising in the 3D domain compared to the 2D domain.
read the caption
Figure 3: Dual-Diff (red) v.s. 2D-Diff (blue) under various T and K = 25.
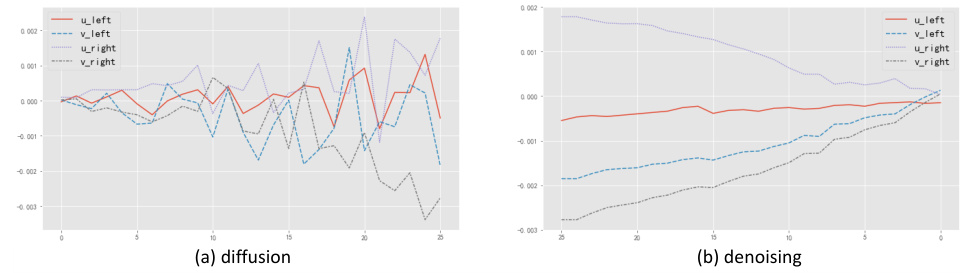
🔼 This figure visualizes the step-wise errors of binocular 2D joints (u, v) during both the forward diffusion and reverse denoising processes. The graph shows how the errors of the left and right u and v coordinates of a single joint (right knee) change over time. (a) shows the diffusion process: noise is incrementally added, increasing the error from the ground truth. (b) shows the denoising process: the denoiser network progressively reduces the noise and error, leading to more accurate pose estimation.
read the caption
Figure 4: Step-wise errors of binocular 2D joints, (u, v)left and (u, v)right, during the diffusion and denoising processes. The joint analyzed is the right knee.
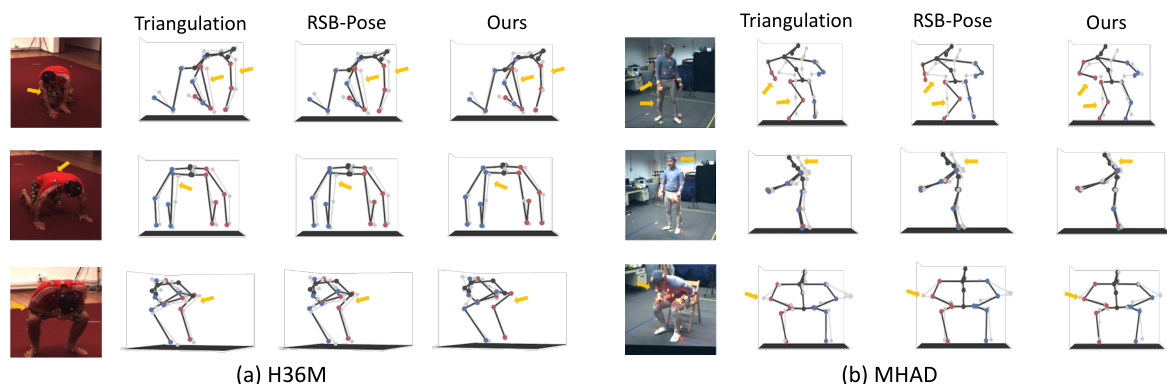
🔼 This figure compares the 3D human pose estimation results of the proposed Dual-Diffusion method against two baseline methods: Triangulation and RSB-Pose. The results are shown for both the H36M and MHAD datasets. The gray skeleton represents the ground truth pose, while the black skeletons represent the estimated poses from each method. Red and blue points indicate joints on the right and left sides, respectively. Yellow arrows highlight areas where the Dual-Diffusion method shows significant improvement over the baselines.
read the caption
Figure 5: Qualitative Comparison with Triangulation and RSB-Pose in 3D Pose Estimation. 2D poses are estimated by RSB-Pose152*. The gray skeleton is the ground truth, while the black represents the estimates. Red and blue points correspond to joints on the right and left sides, respectively. Yellow arrows indicate parts of significant improvement achieved by our method.
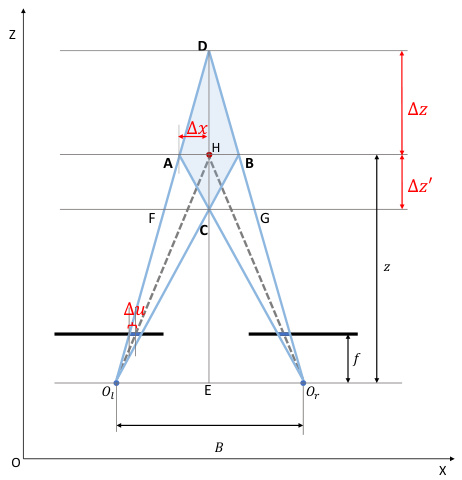
🔼 This figure illustrates the geometric relationship between 2D and 3D uncertainties in a binocular configuration. It shows how the uncertainty in the estimated 2D position of a point (represented by the range Δu) projects into a 3D uncertainty volume (represented by Δx, Δz, and Δz’). Points A, B, C, and D define the boundaries of this 3D uncertainty volume. The analysis in the paper uses this figure to derive mathematical formulas relating the 2D and 3D uncertainties, considering factors like baseline width (B) and depth (z).
read the caption
Figure 6: 3D reconstructing uncertainty range of binocular configuration.
🔼 This figure illustrates the Dual-Diffusion method proposed in the paper. The left panel (a) shows the modeling process, where noise is added to the ground truth 2D poses step-by-step, then triangulated to create noisy 3D poses. The reverse process involves denoising the 3D poses, which are then reprojected back to 2D to ensure consistency. The right panel (b) shows the inference process, where initial 3D poses are denoised iteratively to obtain final accurate 3D and 2D poses.
read the caption
Figure 2: Overview of Dual-Diffusion Method. (a) Modeling: In the forward diffusion process, noise is added to the ground truth binocular 2D poses u0 for T steps, aligning with the distribution of initial estimated 2D poses. During the reverse denoising process, noisy 3D poses are progressively denoised to plausible poses. Geometric mapping is employed to connect 2D and 3D domains. (b) Inference: The initial 3D pose yT, reconstructed from binocular 2D poses uT, is denoised to y0. Then y0 is reprojected to the denoised 2D poses u0. The entire denoising process iterates for K times.
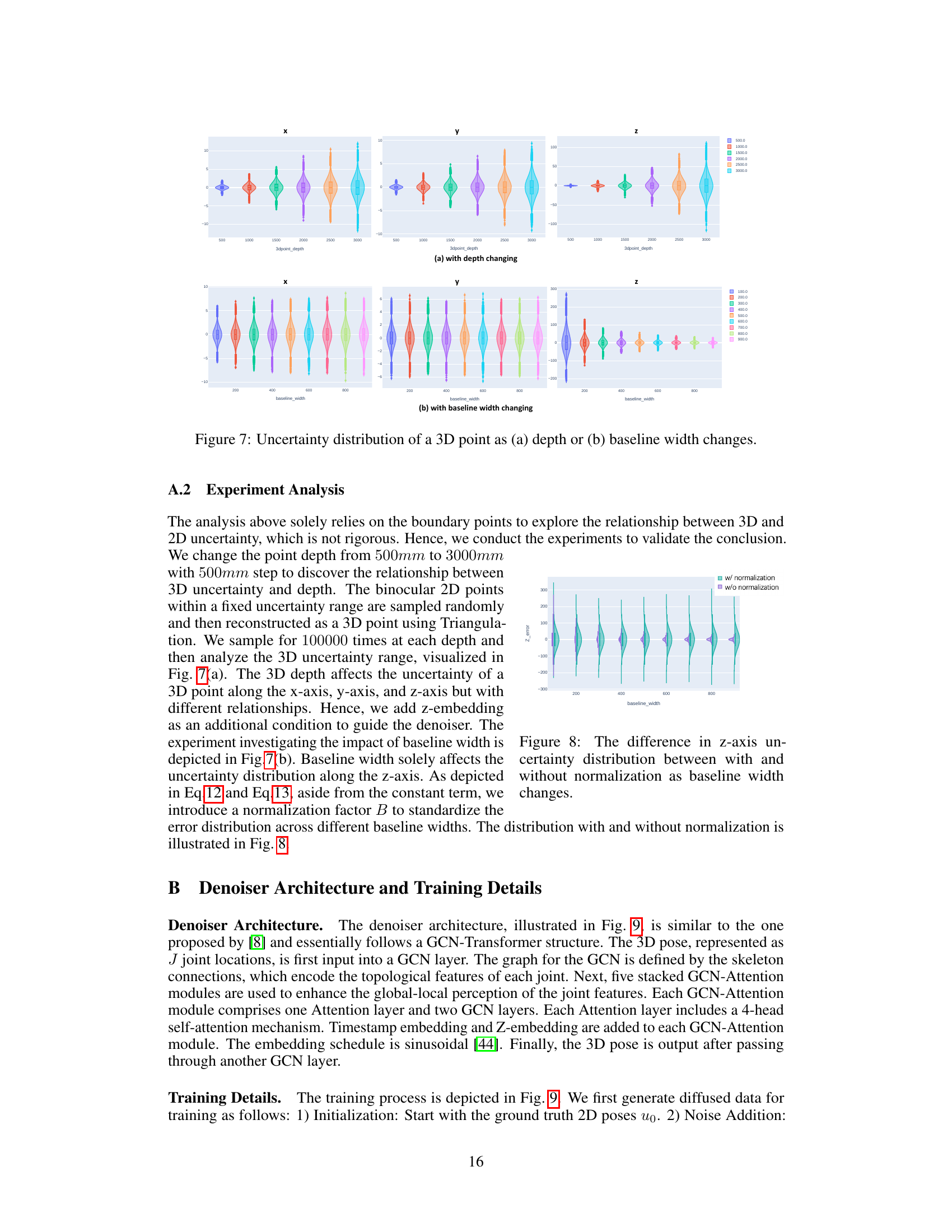
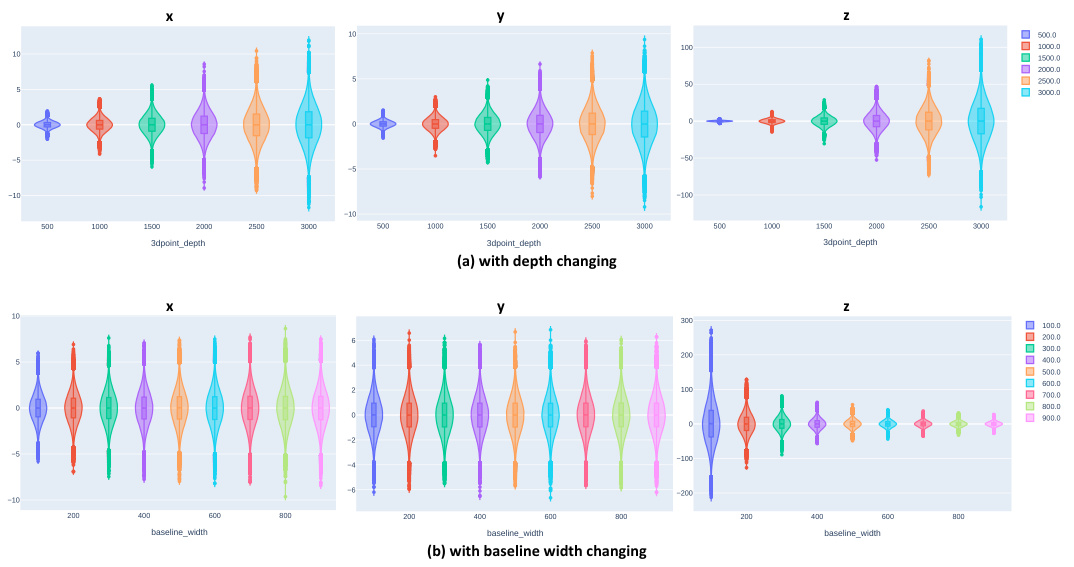
🔼 This figure visualizes the uncertainty distribution of a 3D point reconstructed from binocular 2D poses, showing how this uncertainty changes with varying depth (a) and baseline width (b). The plots show that the depth of the 3D point significantly impacts the uncertainty along all three axes (x, y, z), while the baseline width primarily affects uncertainty along the z-axis. This analysis supports the inclusion of z-embedding as a conditional input to the Dual-Diffusion model and the use of Baseline-width-related pose normalization to handle varying baseline widths.
read the caption
Figure 7: Uncertainty distribution of a 3D point as (a) depth or (b) baseline width changes.

🔼 This figure illustrates the Dual-Diffusion method proposed in the paper. Panel (a) shows the modeling process, detailing how noise is added to the ground truth 2D poses (forward diffusion) and how noisy 3D poses are denoised to plausible results (reverse denoising). Geometric mapping connects the 2D and 3D domains. Panel (b) shows the inference process, illustrating how initial 3D poses are iteratively refined (K times) to produce accurate 3D and 2D poses.
read the caption
Figure 2: Overview of Dual-Diffusion Method. (a) Modeling: In the forward diffusion process, noise is added to the ground truth binocular 2D poses u for T steps, aligning with the distribution of initial estimated 2D poses. During the reverse denoising process, noisy 3D poses are progressively denoised to plausible poses. Geometric mapping is employed to connect 2D and 3D domains. (b) Inference: The initial 3D pose yT, reconstructed from binocular 2D poses uT, is denoised to ỹ0. Then ỹ0 is reprojected to the denoised 2D poses ũ0. The entire denoising process iterates for K times.
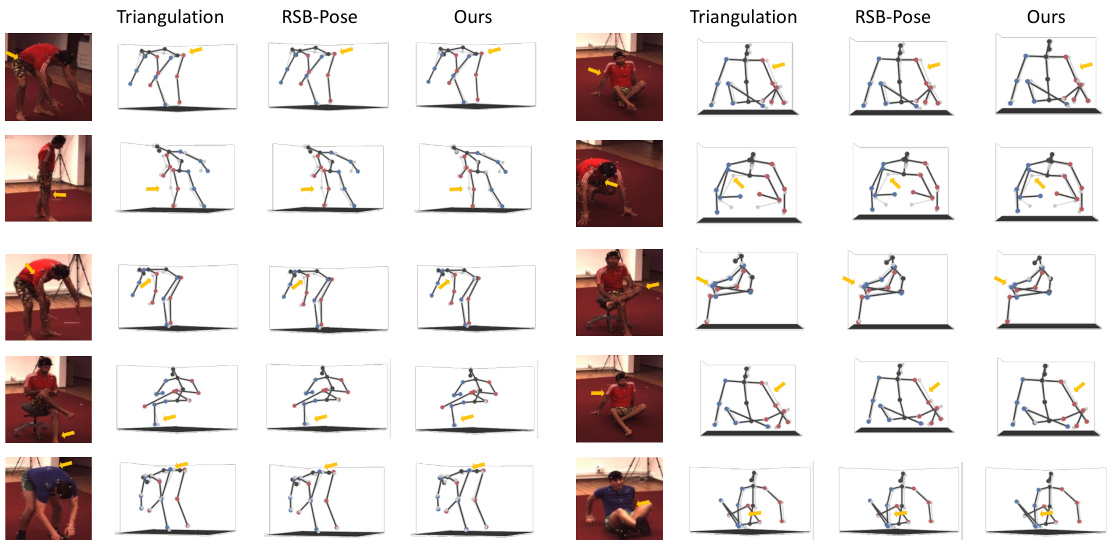
🔼 This figure shows a qualitative comparison of 3D human pose estimation results between the proposed Dual-Diffusion method and two baseline methods (Triangulation and RSB-Pose) on the MHAD and H36M datasets. The ground truth poses are shown in gray, while the estimated poses are shown in black. Red and blue points represent joints on the right and left sides of the body, respectively. Yellow arrows highlight areas where the Dual-Diffusion method shows significant improvement over the baseline methods. The comparison demonstrates the superiority of Dual-Diffusion in accuracy and handling self-occlusions, particularly in challenging poses.
read the caption
Figure 5: Qualitative Comparison with Triangulation and RSB-Pose in 3D Pose Estimation. 2D poses are estimated by RSB-Pose152*. The gray skeleton is the ground truth, while the black represents the estimates. Red and blue points correspond to joints on the right and left sides, respectively. Yellow arrows indicate parts of significant improvement achieved by our method.
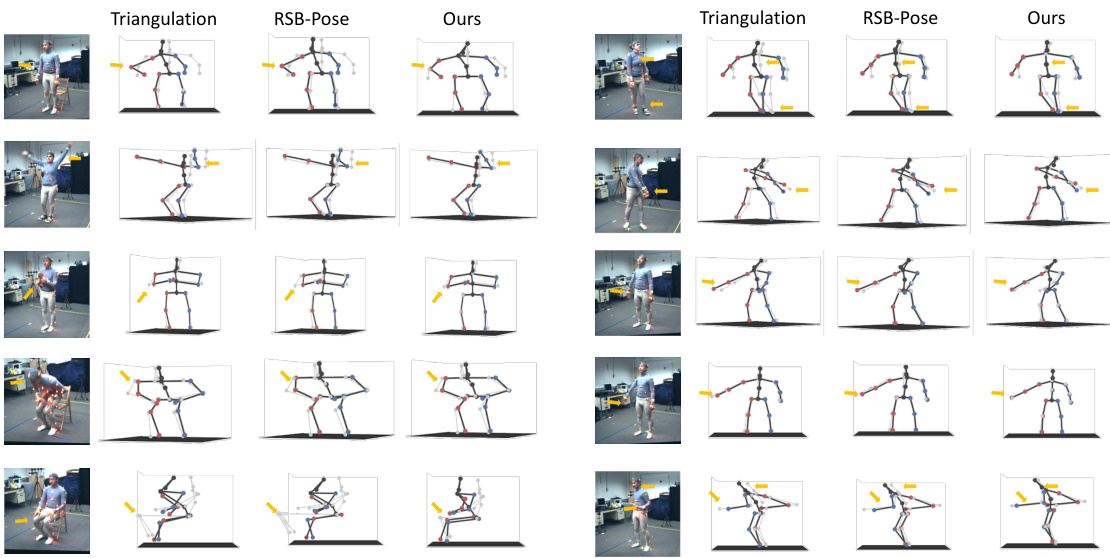
🔼 This figure compares the 3D human pose estimation results of the proposed Dual-Diffusion method against two baseline methods: Triangulation and RSB-Pose. The ground truth poses are shown in gray, while the estimations from each method are in black. Red and blue points differentiate right and left joints. Yellow arrows highlight areas where Dual-Diffusion significantly outperforms the baselines.
read the caption
Figure 5: Qualitative Comparison with Triangulation and RSB-Pose in 3D Pose Estimation. 2D poses are estimated by RSB-Pose152*. The gray skeleton is the ground truth, while the black represents the estimates. Red and blue points correspond to joints on the right and left sides, respectively. Yellow arrows indicate parts of significant improvement achieved by our method.
More on tables
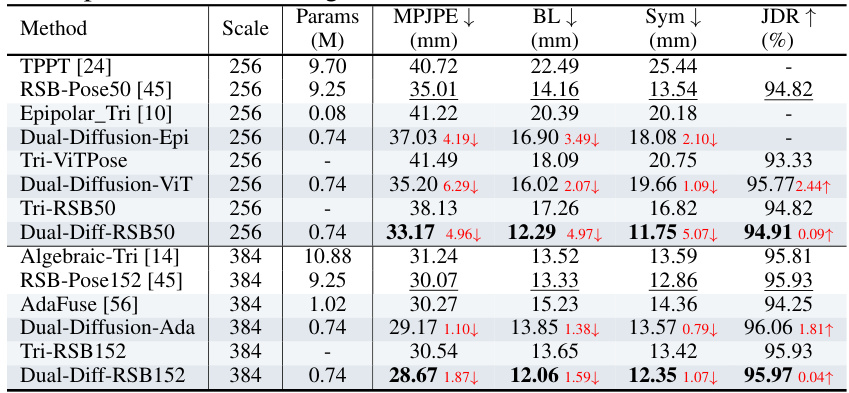
🔼 This table presents a quantitative comparison of the proposed Dual-Diffusion model’s performance on the Human3.6M (H36M) dataset against several baseline and state-of-the-art methods. The metrics evaluated include Mean Per Joint Position Error (MPJPE), Bone Length error (BL), Symmetry error (Sym), and Joint Detection Rate (JDR). The table is broken down by different model configurations and image scales, allowing for analysis of the model’s effectiveness across different scenarios and computational costs. The number of parameters (excluding the backbone network) is also provided for each method.
read the caption
Table 2: Quantitative Comparison on H36M. Params is the number of model parameters excluding the backbone.

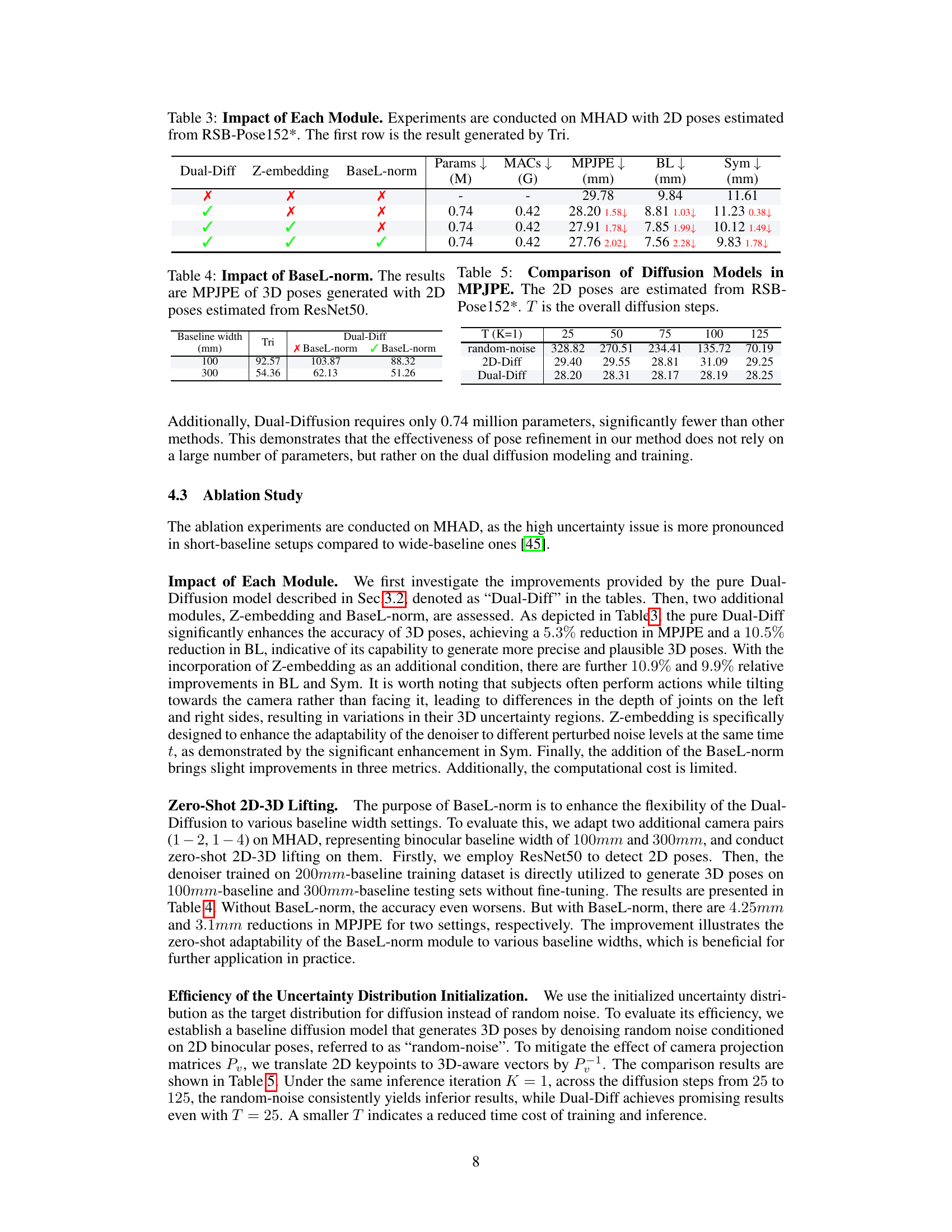
🔼 This table presents an ablation study evaluating the impact of each module (Z-embedding and BaseL-norm) in the Dual-Diffusion model on the MHAD dataset. The results are compared against the baseline Triangulation method. It shows the effectiveness of each component in improving the accuracy of 3D pose estimation, measured by MPJPE, BL, and Sym metrics. The table also reports the model parameters and MACs for each configuration.
read the caption
Table 3: Impact of Each Module. Experiments are conducted on MHAD with 2D poses estimated from RSB-Pose152*. The first row is the result generated by Tri.

🔼 This table shows the impact of the baseline width normalization (BaseL-norm) module on the performance of the Dual-Diffusion model. The results presented are the mean per joint position error (MPJPE) for 3D poses generated using 2D poses estimated by the ResNet50 model. The baseline width is varied (100mm and 300mm), comparing results with and without the BaseL-norm module enabled. This highlights the effectiveness of BaseL-norm in adapting the model’s performance across different baseline settings.
read the caption
Table 4: Impact of BaseL-norm. The results are MPJPE of 3D poses generated with 2D poses estimated from ResNet50.

🔼 This table compares the performance of three different diffusion models (random-noise, 2D-Diff, and Dual-Diff) in terms of Mean Per Joint Position Error (MPJPE) for different numbers of diffusion steps (T). The 2D poses used as input to these models are estimated using the RSB-Pose152* method. The results show how the different models perform in reducing the uncertainty in 3D pose estimation as the number of diffusion steps changes. The Dual-Diff model, which denoises both 2D and 3D poses simultaneously, shows the best performance across all values of T.
read the caption
Table 5: Comparison of Diffusion Models in MPJPE. The 2D poses are estimated from RSB-Pose152*. T is the overall diffusion steps.

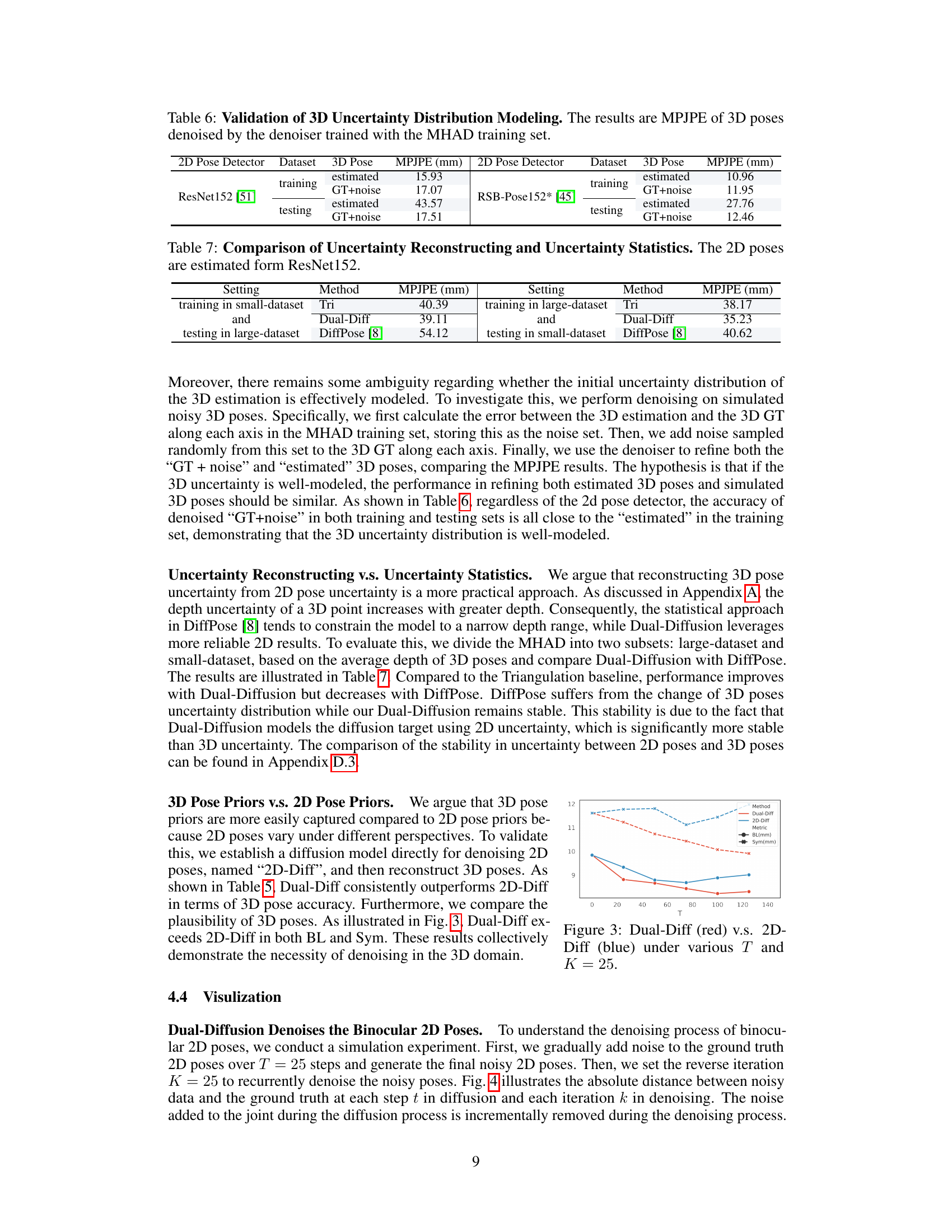
🔼 This table presents the Mean Per Joint Position Error (MPJPE) results for 3D human pose estimation. The denoiser model was trained on the MHAD dataset. It shows the MPJPE for both estimated 3D poses and simulated noisy 3D poses (GT+noise). The results are broken down by 2D pose detector used (ResNet152 and RSB-Pose152*), and whether the poses are from the training or testing set. This table aims to validate how well the model captures the uncertainty of the initial 3D pose distribution.
read the caption
Table 6: Validation of 3D Uncertainty Distribution Modeling. The results are MPJPE of 3D poses denoised by the denoiser trained with the MHAD training set.

🔼 This table compares the performance of Triangulation and Dual-Diffusion methods in reconstructing 3D pose uncertainty, using different training and testing dataset sizes. The goal is to show that Dual-Diffusion is more robust to the changes in training data size compared to Triangulation and DiffPose method.
read the caption
Table 7: Comparison of Uncertainty Reconstructing and Uncertainty Statistics. The 2D poses are estimated form ResNet152.

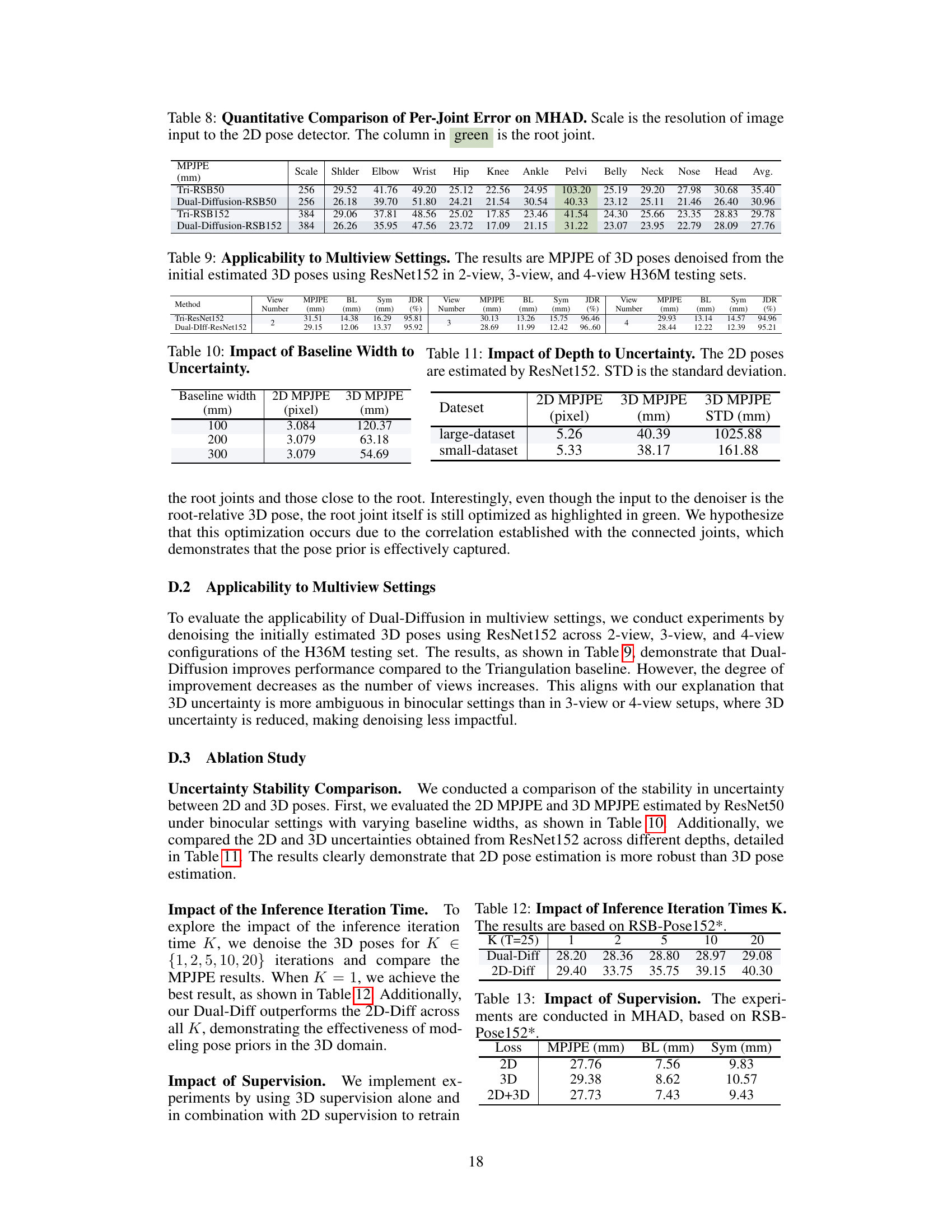
🔼 This table presents a quantitative comparison of per-joint errors on the MHAD dataset for 3D human pose estimation. It compares the performance of the Triangulation method and the proposed Dual-Diffusion method using two different scales (256 and 384) for image resolution. The errors are measured using Mean Per Joint Position Error (MPJPE) and are broken down for individual joints (Shoulder, Elbow, Wrist, Hip, Knee, Ankle, Pelvis, Belly, Neck, Nose, Head) providing a detailed view of the method’s performance at each joint. The root joint’s MPJPE is highlighted in green for emphasis.
read the caption
Table 8: Quantitative Comparison of Per-Joint Error on MHAD. Scale is the resolution of image input to the 2D pose detector. The column in green is the root joint.

🔼 This table shows the performance of Dual-Diffusion on multiview settings (2, 3, and 4 views). It demonstrates the model’s generalizability to different numbers of cameras. The results are compared against a Triangulation baseline, showing the improvement achieved by Dual-Diffusion in each multiview setting. The metrics used include MPJPE, BL, Sym, and JDR.
read the caption
Table 9: Applicability to Multiview Settings. The results are MPJPE of 3D poses denoised from the initial estimated 3D poses using ResNet152 in 2-view, 3-view, and 4-view H36M testing sets.

🔼 This table shows the impact of baseline width on the uncertainty of 2D and 3D pose estimations. As the baseline width increases from 100mm to 300mm, the MPJPE (Mean Per Joint Position Error) for both 2D and 3D poses decreases. This indicates that a wider baseline leads to more accurate pose estimations, likely due to improved depth estimation in the binocular setup.
read the caption
Table 10: Impact of Baseline Width to Uncertainty.
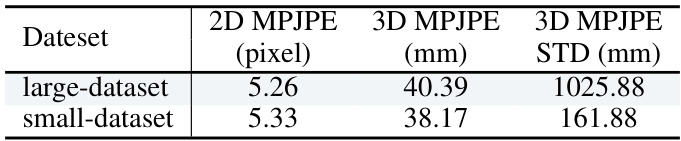
🔼 This table presents the impact of depth on uncertainty in 3D pose estimation using ResNet152 as a 2D pose detector. It shows the standard deviation (STD) of 2D and 3D MPJPE for both large and small datasets at various depths, demonstrating the relationship between 3D uncertainty and depth.
read the caption
Table 11: Impact of Depth to Uncertainty. The 2D poses are estimated by ResNet152. STD is the standard deviation.

🔼 This table shows the impact of the number of inference iterations (K) on the performance of the Dual-Diffusion and 2D-Diff models. The results, measured by MPJPE (Mean Per Joint Position Error) in mm, are shown for different values of K while keeping the diffusion steps (T) constant at 25. The table demonstrates the effect of iterative denoising on the accuracy of 3D pose estimation.
read the caption
Table 12: Impact of Inference Iteration Times K. The results are based on RSB-Pose152*.
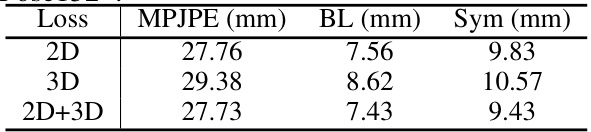
🔼 This table presents the ablation study results on the MHAD dataset using the RSB-Pose152* as a 2D pose detector. It compares the performance of three different supervision strategies: using only 2D supervision, only 3D supervision, and using both 2D and 3D supervision. The results are measured by MPJPE, BL, and Sym, showing the impact of different supervision methods on the accuracy and plausibility of 3D pose estimation.
read the caption
Table 13: Impact of Supervision. The experiments are conducted in MHAD, based on RSB-Pose152*.
Full paper#