↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Existing social network embedding models often oversimplify link formation, neglecting the interplay of homophily (similarity-driven connections) and social influence (popularity-driven connections). These limitations hinder accurate representation of network structure and topology, impacting downstream tasks like link prediction and node classification. Moreover, many models rely on single, Euclidean spaces, which fail to capture the curved geometry of real-world social networks (cycles and hierarchies). This paper addresses these issues by proposing a novel approach.
The proposed model, NMM-GNN, tackles these limitations by using a mixture model that incorporates both homophily and social influence. Crucially, it leverages non-Euclidean geometric spaces: spherical space for homophily and hyperbolic space for social influence, better capturing the inherent curved structure of social networks. By using a graph-based variational autoencoder (VAE), NMM-GNN learns node embeddings through a unified framework that integrates non-Euclidean Gaussian priors and a space unification loss, aligning the distinct spaces seamlessly. The extensive empirical results across multiple datasets demonstrate that NMM-GNN substantially outperforms current state-of-the-art models on both link prediction and node classification tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on social network analysis, graph embedding, and generative models. It significantly advances the state-of-the-art by introducing a novel non-Euclidean approach and a unified framework that captures both homophily and social influence. The improved accuracy and scalability of the proposed model open up exciting new avenues for understanding and modeling complex social networks. This work is highly relevant to researchers exploring non-Euclidean geometric spaces for network embedding and those developing new graph generative models.
Visual Insights#
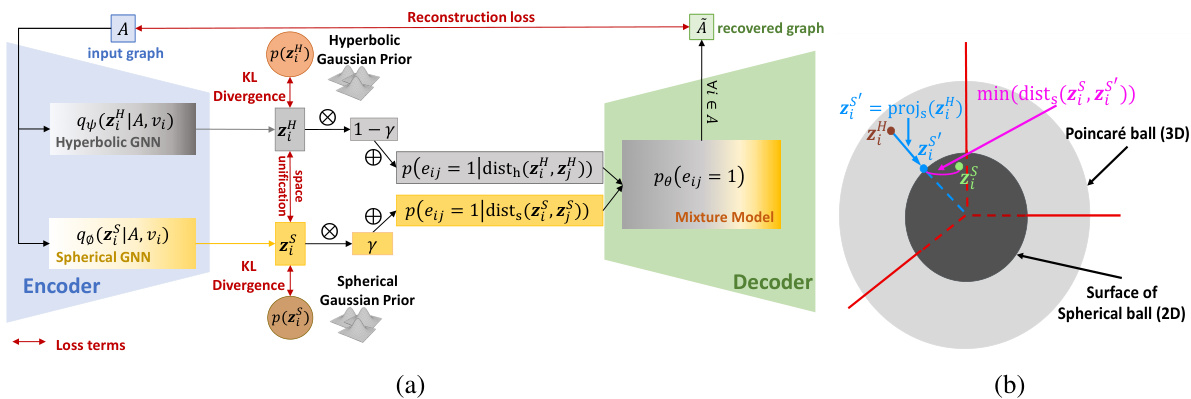
This figure shows the architecture of the Non-Euclidean Mixture Model (NMM) with a variational autoencoder (VAE) framework. Panel (a) provides a high-level overview of the model, showing how hyperbolic and spherical graph neural networks (GNNs) are used to encode node embeddings in different spaces, which are then combined using a mixture model. Panel (b) details the space unification loss component, illustrating how embeddings from the hyperbolic space are projected to the spherical space to ensure consistency between the two representations.
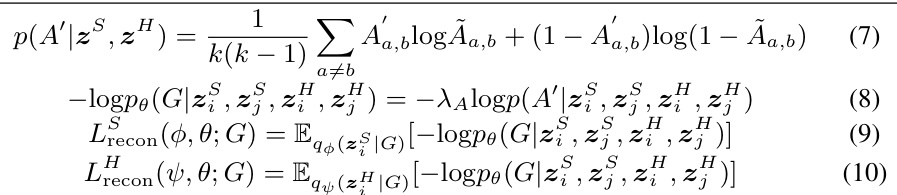
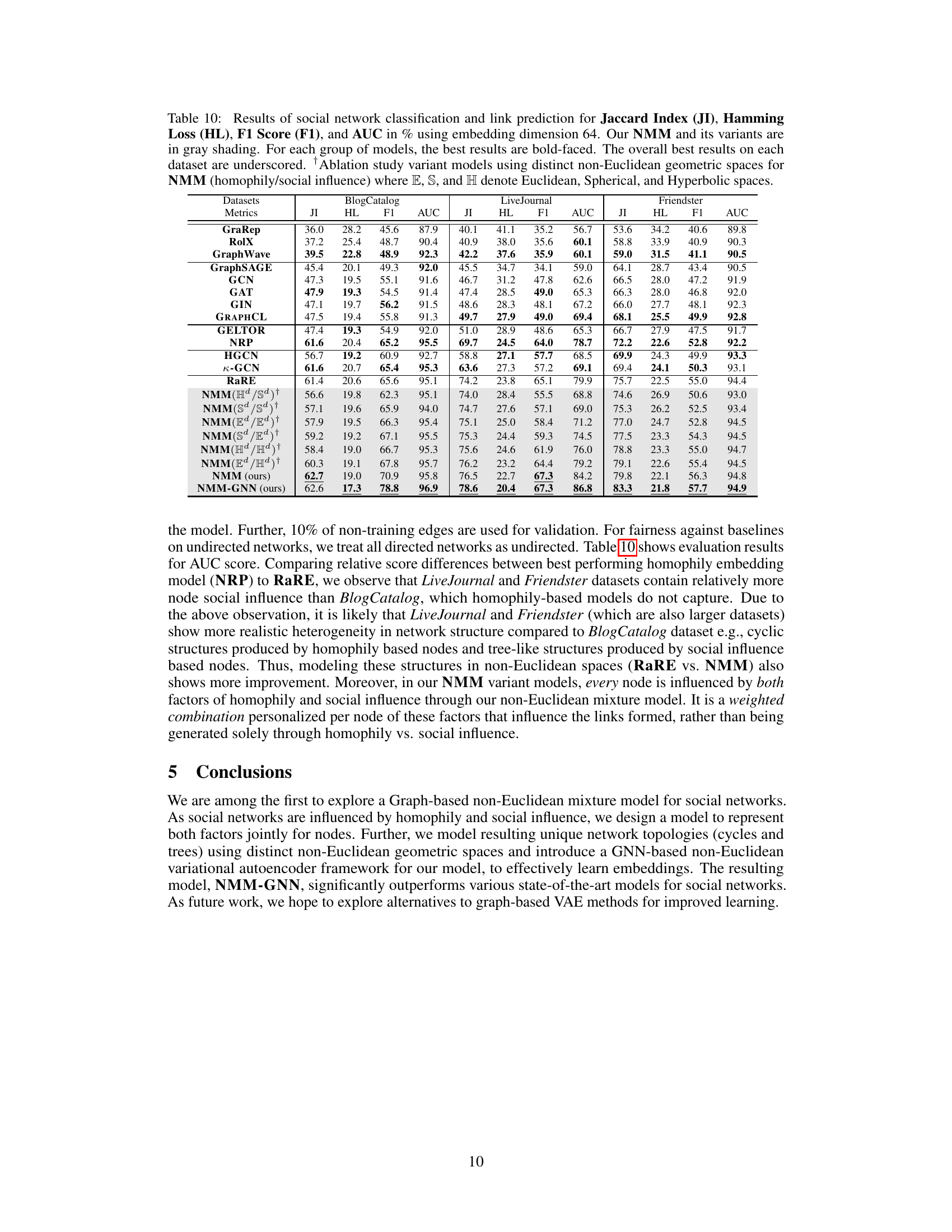
This table presents the results of social network classification and link prediction experiments using different models, including the proposed NMM and its variants. The evaluation metrics used are Jaccard Index, Hamming Loss, F1 Score, and AUC. The table highlights the best-performing models for each dataset and metric, distinguishing the proposed models (NMM and variations) with gray shading. Ablation studies using different combinations of Euclidean, spherical, and hyperbolic spaces are also included.
In-depth insights#
Non-Euclidean Embedding#
Non-Euclidean embeddings offer a powerful approach to represent data with complex relationships that are not well-captured by traditional Euclidean methods. By leveraging geometries like hyperbolic and spherical spaces, these methods can model hierarchical structures and cyclical patterns, respectively, inherent in many real-world networks. This is particularly relevant for social networks, where homophily (similarity-based connections) creates cycles and social influence generates hierarchical structures. A key advantage is the ability to model these distinct network phenomena within their natural geometric context. The use of non-Euclidean spaces allows for more accurate and insightful representations, as compared to forcing complex data onto a flat, Euclidean space. The application of graph neural networks (GNNs) within these non-Euclidean frameworks further enhances model capabilities, enabling efficient learning of node embeddings and prediction of links in large-scale networks. However, challenges remain in unifying the different non-Euclidean spaces and aligning the embeddings across them for a holistic network representation.
Mixture Model#
The core of this research lies in its novel application of a mixture model to represent the multifaceted nature of social network link formation. Instead of relying on a single generative mechanism, the authors cleverly integrate two distinct factors: homophily (similarity-driven connections) and social influence (popularity-driven connections). This dual-factor approach is crucial because it acknowledges the complex interplay of these forces in shaping real-world networks. The model’s innovative aspect is its use of non-Euclidean geometries: homophily is modeled in spherical space, capturing the cyclical nature of connections among similar nodes, while social influence is modeled in hyperbolic space, reflecting the hierarchical structure resulting from the influence of popular individuals. The integration of these distinct geometric spaces via a specialized projection mechanism represents a significant advancement over previous approaches that rely solely on Euclidean embeddings. This mixture model, therefore, offers a richer and more nuanced representation of network dynamics, ultimately leading to improved performance in link prediction and network generation tasks.
NMM-GNN Framework#
The NMM-GNN framework represents a novel approach to social network embedding by integrating a Non-Euclidean Mixture Model (NMM) with a graph neural network (GNN) based variational autoencoder (VAE). NMM elegantly captures the dual nature of link formation, driven by both homophily (similarity-based connections) and social influence (popularity-based connections), modeling them distinctly in spherical and hyperbolic spaces, respectively. The GNN encoder within the VAE framework learns node embeddings in these non-Euclidean spaces, effectively capturing the cyclical structures inherent in homophily and the hierarchical structures associated with social influence. A critical component is the space unification loss, which aligns the spherical and hyperbolic representations, ensuring a consistent unified embedding for each node despite the different geometric contexts. This framework demonstrates superior performance over state-of-the-art baselines, showcasing its ability to learn more informative and topologically accurate social network embeddings.
Empirical Validation#
An empirical validation section in a research paper would rigorously test the proposed model’s performance. It would involve selecting appropriate datasets, establishing clear evaluation metrics (like precision, recall, F1-score, AUC), and comparing the model’s results against established baselines. A strong validation would include ablation studies, systematically removing components to isolate the contribution of each part. Statistical significance testing is crucial to determine if observed improvements are not simply due to chance. The choice of datasets is vital; using both publicly available and private datasets enhances confidence in the model’s generalization. Careful attention to experimental setup, including parameter tuning strategies and the handling of hyperparameters, ensures reproducibility. The results should be clearly presented, and the limitations of the empirical validation (e.g., dataset biases, specific evaluation metrics) should be transparently acknowledged.
Future Directions#
Future research could explore several promising avenues. Extending NMM-GNN to handle temporal dynamics in social networks is crucial, as relationships evolve over time. This would involve incorporating time-series data and developing appropriate temporal graph neural network architectures. Another key direction is improving scalability to handle even larger networks efficiently. This might involve exploring more efficient graph embedding techniques or distributed training strategies. Investigating alternative loss functions could further improve model performance and stability. Finally, a deeper investigation into the interpretability of the learned embeddings would greatly enhance the model’s usability and provide more valuable insights into the complex mechanisms underlying social network formation. Specifically, developing methods to understand the contributions of homophily and social influence to individual link formations could yield significant benefits.
More visual insights#
More on figures
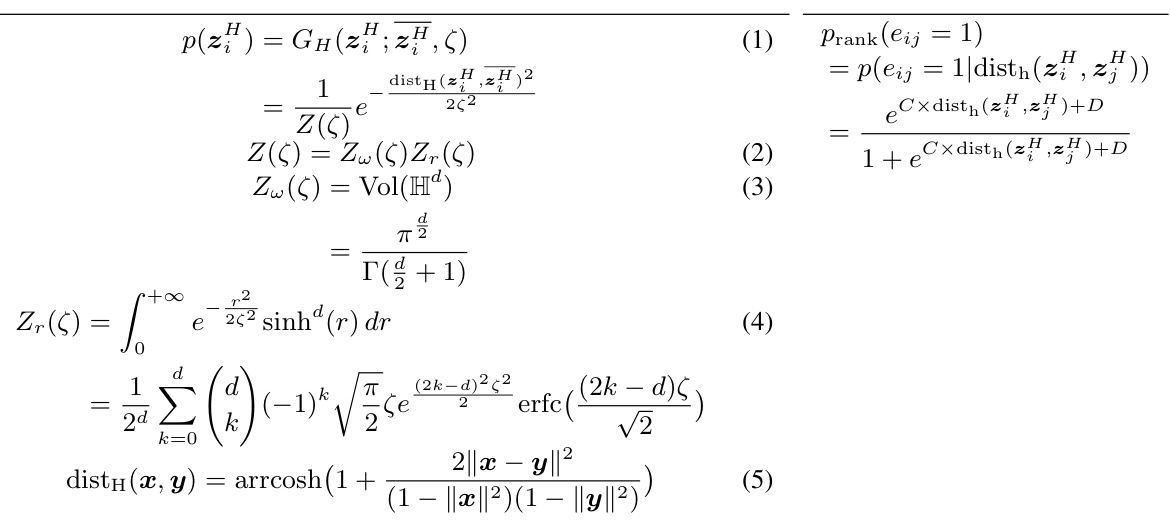
This figure shows the architecture of the NMM-GNN model, which combines a non-Euclidean mixture model with a variational autoencoder (VAE) framework. Panel (a) provides a high-level overview of the model, highlighting the encoder (using spherical and hyperbolic GNNs), mixture model, and decoder components. Panel (b) zooms in on the space unification loss, illustrating how embeddings from hyperbolic space are projected into spherical space to ensure consistency and alignment between the different geometric representations.

This figure shows the architecture of the NMM-GNN model, which combines a non-Euclidean Mixture Model with a variational autoencoder (VAE) framework. Panel (a) presents a high-level overview of the model, illustrating the encoder (using spherical and hyperbolic GNNs), the mixture model (combining homophily and social influence factors), and the decoder. Panel (b) focuses on the space unification loss, which ensures alignment between embeddings in the hyperbolic and spherical spaces by minimizing the geodesic distance between the projection of a hyperbolic embedding onto the spherical space and its corresponding embedding in the spherical space. This alignment is crucial for effectively integrating information from both spaces.

This figure shows the architecture of the proposed Non-Euclidean Mixture Model (NMM) with a Graph Neural Network (GNN) based Variational Autoencoder (VAE) framework called NMM-GNN. The figure is divided into two subfigures. (a) shows a general overview of the framework, highlighting its components such as the encoder, decoder and mixture model. The encoder consists of spherical and hyperbolic GNNs. The decoder uses a mixture model to combine the embeddings from the spherical and hyperbolic spaces to predict link probabilities. (b) illustrates the space unification loss component which ensures alignment between the two non-Euclidean spaces. A node’s embedding in the hyperbolic space (zL) is projected onto the spherical space (zS) to minimize the geodesic distance between the projected point and the node’s existing spherical representation. This ensures consistency between the representations in the two distinct spaces.
This figure presents the results of ablation studies conducted to analyze the impact of different components and design choices in the proposed NMM-GNN model. (a) shows a comparison of the AUC scores for the full NMM model and its deconstructed homophily-only (NMMhom) and social influence-only (NMMrank) components across three datasets (BC, LJ, F). (b) illustrates the inductive reasoning capability of NMM-GNN compared to RaRE on the LiveJournal dataset, showing the AUC scores for varying percentages of training nodes. (c) evaluates the effect of the space unification loss (SUL) component on the model’s performance across five datasets (WC, BC, LJ, WH, F).
More on tables
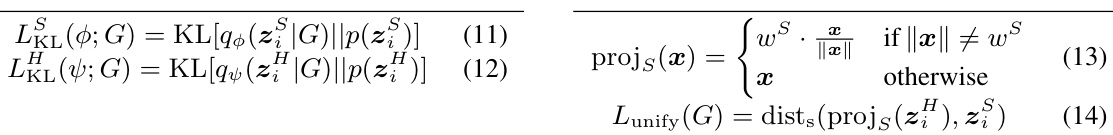
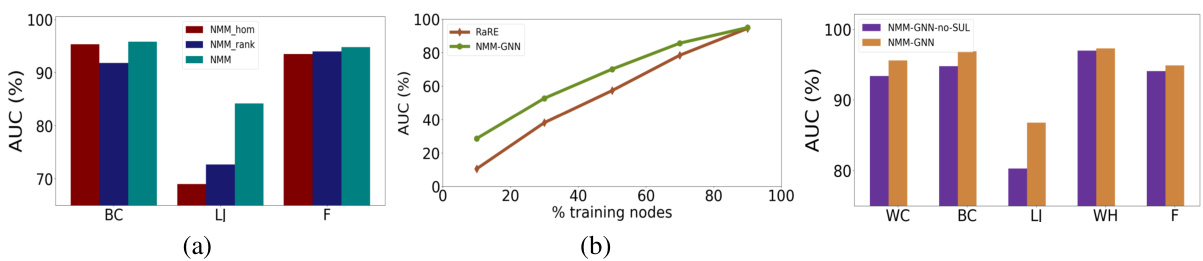
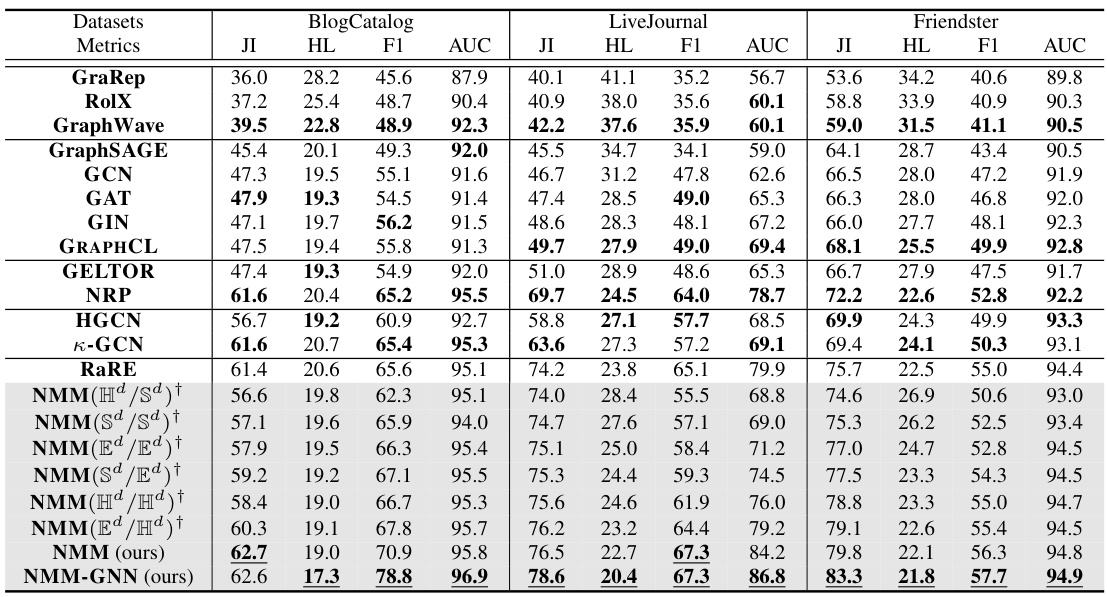
This table presents the results of social network classification and link prediction experiments using different embedding models. The models are evaluated based on four metrics: Jaccard Index, Hamming Loss, F1-score, and AUC. The table compares the performance of the proposed Non-Euclidean Mixture Model (NMM) and its variations against several baseline models. The NMM variants explore different combinations of Euclidean, Spherical, and Hyperbolic spaces for representing homophily and social influence, showing the impact of geometric space selection on model performance. The best results for each model group and overall best results are highlighted.

This table presents the statistics of three real-world social network datasets used in the paper’s experiments: BlogCatalog, LiveJournal, and Friendster. For each dataset, it lists the number of vertices (nodes), the number of edges, whether the graph is directed or undirected, and the number of classes (for multi-label classification tasks). The Friendster dataset is notably larger than the others.

This table categorizes and describes various baseline models used for comparison in the paper. The categories include structural embedding models, GNN embedding models (in Euclidean and non-Euclidean spaces), homophily-based embedding models, and mixture models that consider both homophily and social influence. For each model, a brief description of its approach and relevant citation are provided.
This table presents the results of social network classification and link prediction using various models, including the proposed NMM and its variants. The performance is evaluated using four metrics: Jaccard Index, Hamming Loss, F1 Score, and AUC. The embedding dimension is fixed at 64. The table highlights the best-performing models within each category and overall. Variants of NMM that use different combinations of Euclidean, Spherical, and Hyperbolic spaces are also included in the ablation study.

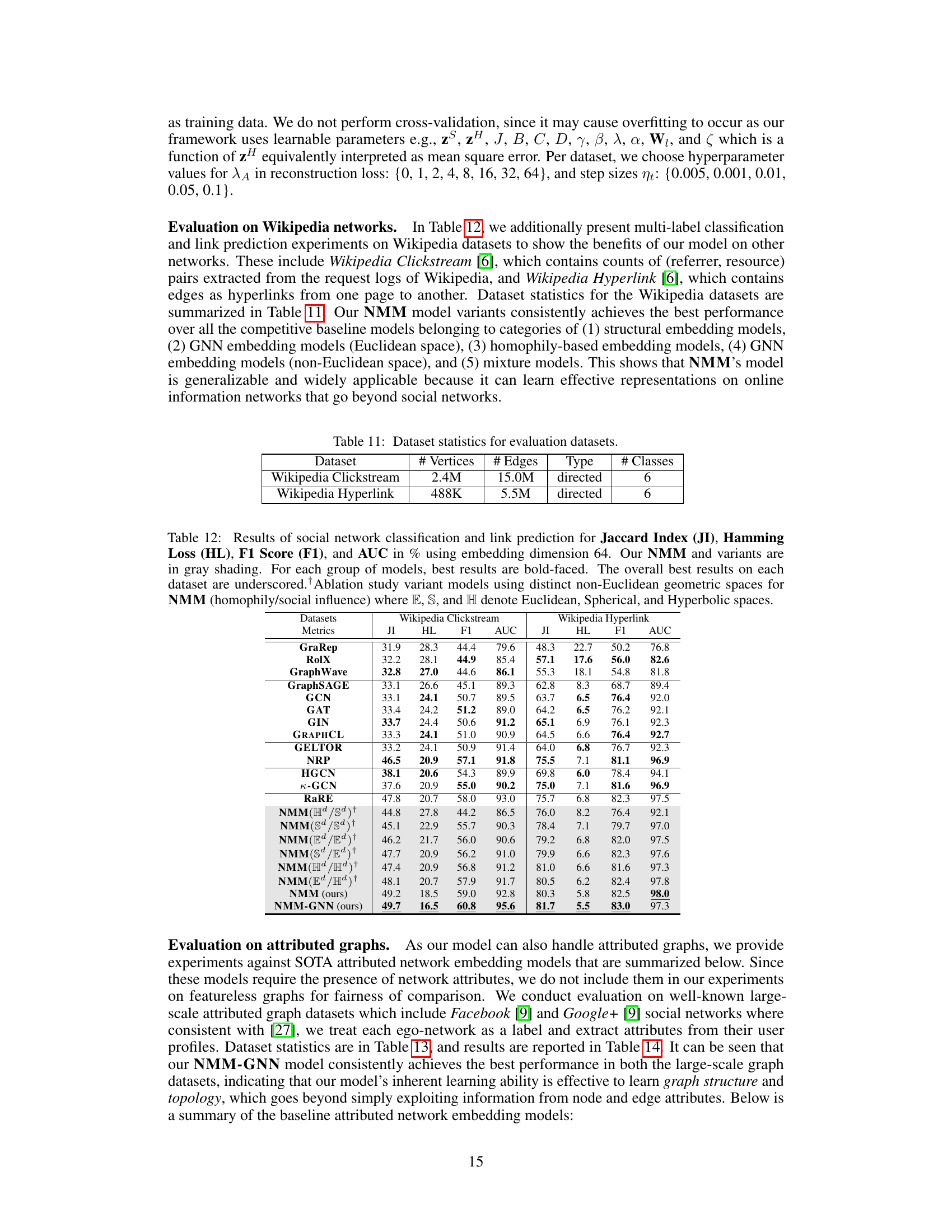
This table provides the number of vertices, edges, graph type (directed or undirected), and number of classes for two Wikipedia datasets: Wikipedia Clickstream and Wikipedia Hyperlink. These datasets were used in the experiments to evaluate the model’s performance on a different type of network data than the main social network datasets.
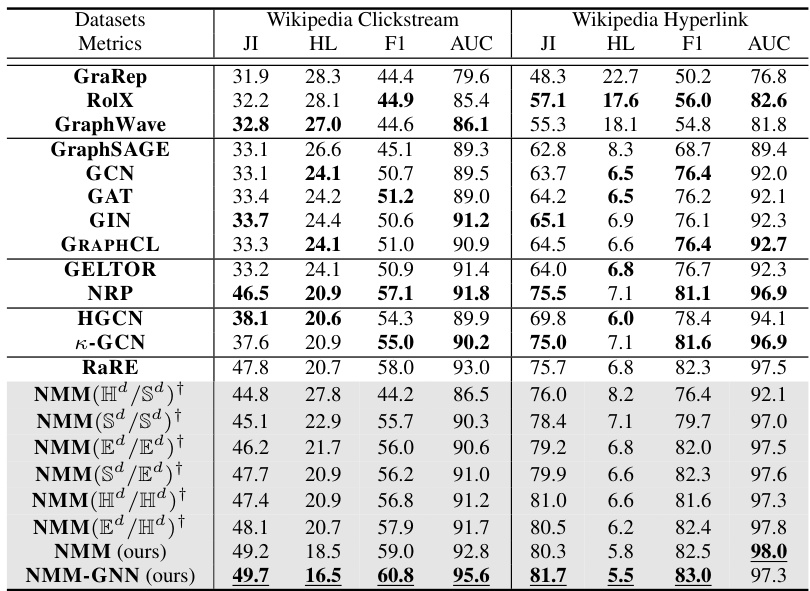
This table presents the results of social network classification and link prediction experiments using different embedding models. The metrics used are Jaccard Index (JI), Hamming Loss (HL), F1 Score (F1), and AUC (Area Under the ROC Curve). The embedding dimension was fixed at 64. The table compares the performance of the proposed Non-Euclidean Mixture Model (NMM) and its variants against several state-of-the-art baselines. Different variants of NMM use various combinations of Euclidean, spherical, and hyperbolic spaces for representing homophily and social influence. The best results for each group of models and the overall best results for each dataset are highlighted.

This table presents the characteristics of the datasets used in the experiments evaluating the performance of the proposed model and baseline models on attributed graphs. The datasets include Facebook and Google+, and the characteristics presented are: number of vertices (nodes), number of edges, number of attributes per node, graph type (directed or undirected), and number of classes for multi-label classification.

This table presents the results of social network classification and link prediction experiments using the proposed NMM-GNN model and several baseline models. The metrics used are Jaccard Index (JI), Hamming Loss (HL), F1-Score (F1), and Area Under the ROC Curve (AUC). The table includes results for three different datasets: BlogCatalog, LiveJournal, and Friendster. The performance of NMM-GNN is compared to various baseline models, categorized by their approach to embedding, with the best results in each category highlighted. Several ablation study variants of NMM using different combinations of Euclidean, spherical, and hyperbolic spaces for homophily and social influence modeling are also included for comparison.
Full paper#