↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
High-dimensional data analysis often involves solving optimization problems with regularizers that enforce structural properties, such as sparsity. Classical approaches use non-smooth penalties, leading to computational challenges. Recent works employ Hadamard over-parameterization for smooth, non-convex formulations, improving numerical stability and convergence. However, theoretical understanding of their convergence remains limited. This research focuses on the challenges of existing approaches in handling high-dimensional datasets, especially when the underlying signals are sparse or exhibit group sparsity. Many existing analyses only provide convergence guarantees or focus on worst-case scenarios, without characterizing the statistical properties of the solutions.
This paper presents a unified asymptotic analysis for a family of algorithms including iteratively reweighted least squares (IRLS), and linear recursive feature machines (lin-RFM). The analysis operates in a batched setting with i.i.d. Gaussian covariates, showing that with appropriate reweighting, these algorithms can achieve favorable performance in just a few iterations. Furthermore, the study extends to group-sparse recovery, proving that group-sparse reweighting significantly improves accuracy. The results are validated through simulations, showcasing strong alignment between theoretical predictions and empirical observations. The work provides a rigorous understanding of the behavior of the algorithms, revealing insights into their convergence and sample complexity.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in high-dimensional statistics and machine learning because it offers precise asymptotic analysis of iterative algorithms for linear diagonal networks, a common architecture in modern machine learning. The findings have implications for sparse recovery, feature learning, and understanding the convergence behavior of non-convex optimization methods, particularly in high-dimensional settings. It bridges the gap between theoretical guarantees and empirical observations, opening up new avenues for improving the efficiency and performance of machine learning algorithms.
Visual Insights#
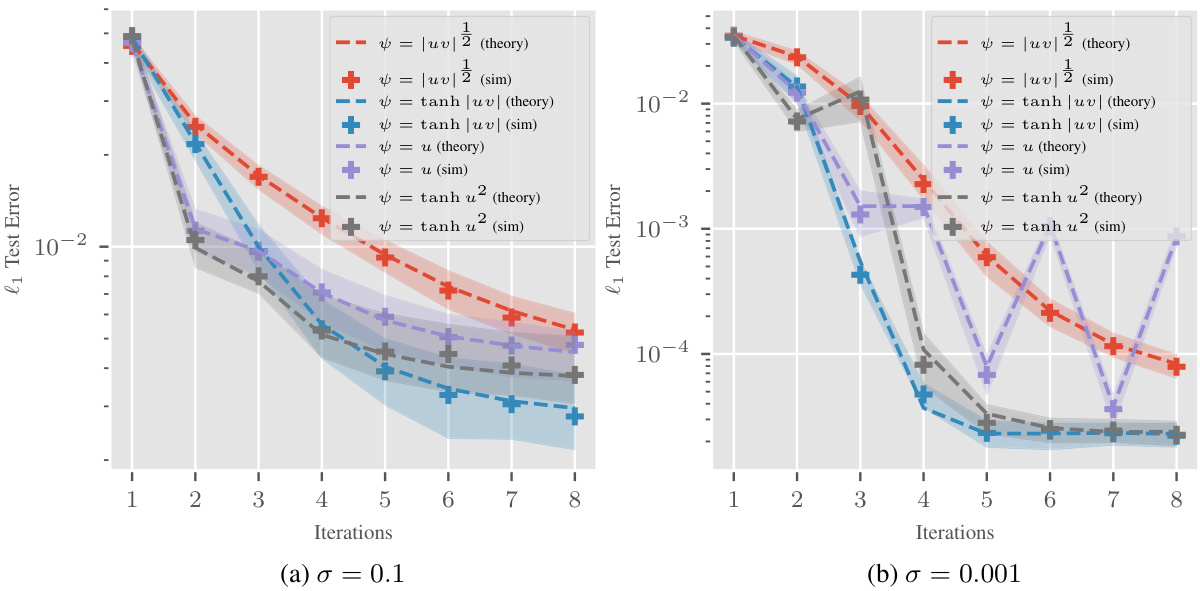
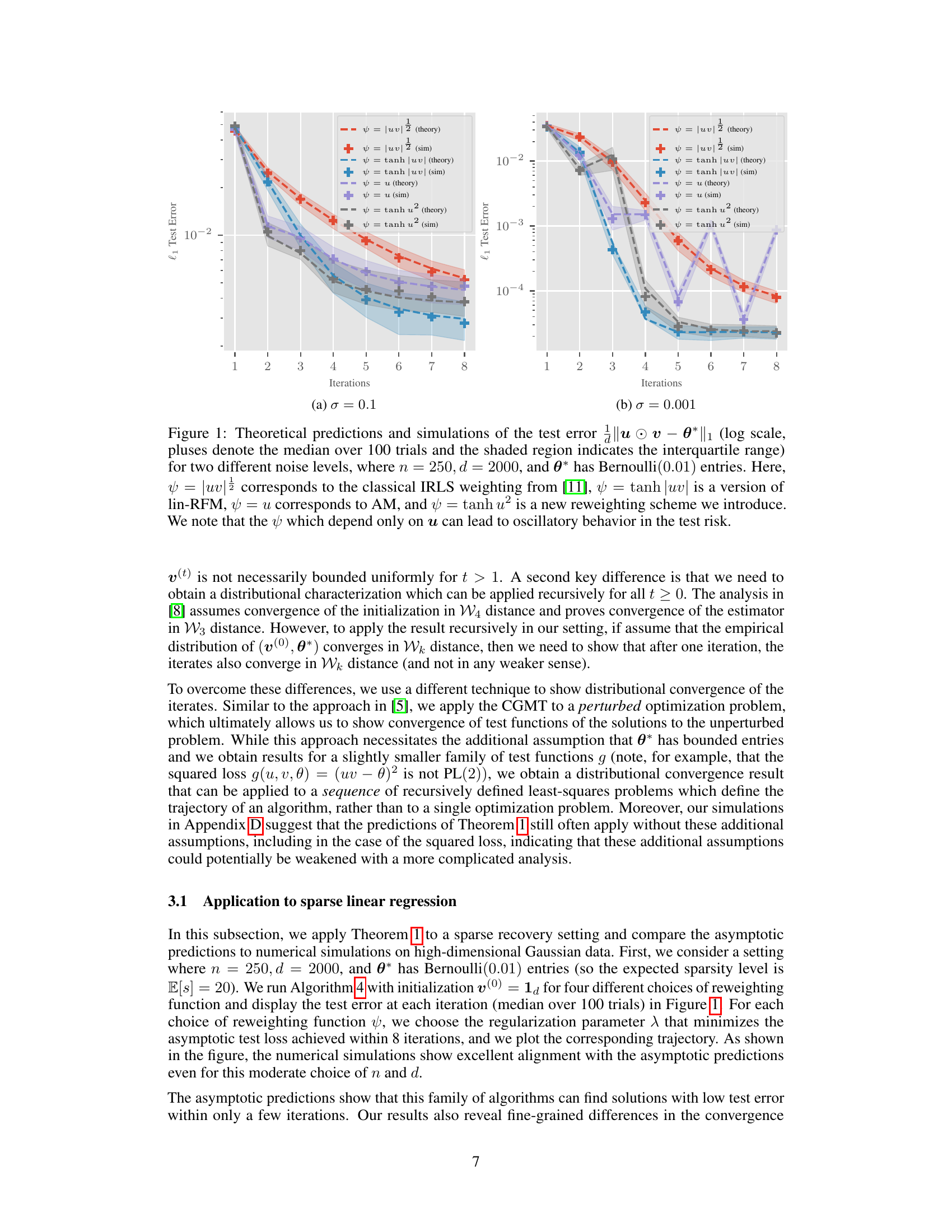
This figure compares theoretical predictions and simulation results for the l1 test error and mean squared error in sparse linear regression for several choices of reweighting function (ψ). The left panel shows results for reweighting functions that are not uniformly bounded, while the right panel shows results for the squared error. The figure demonstrates that the asymptotic analysis provides accurate predictions even for functions that violate the boundedness assumption, showcasing the robustness and generalizability of the theoretical findings.

This table lists three algorithms that can be written in the form of equation (4) from the paper. It shows how different choices of the reweighting function ψ(u, v) lead to different algorithms. Specifically, it shows how the choice of ψ(u, v) results in Alternating minimization, reparameterized IRLS, and linear recursive feature machines.
In-depth insights#
Asymptotic Analysis#
An asymptotic analysis in a research paper provides crucial insights by examining the behavior of a system as certain parameters (like the number of data points or dimensions) approach extreme values (infinity or zero). This technique simplifies complex models, revealing fundamental trends and often yielding closed-form solutions or approximations. For example, in high-dimensional statistics, asymptotic analysis helps determine if an estimator is consistent or efficient, which are not always straightforward to ascertain through exact finite-sample calculations. The strength of such analysis lies in its ability to generalize beyond specific instances, focusing on long-term behavior. However, limitations also exist. Asymptotic results may not accurately reflect the system’s behavior in small-sample or finite-dimensional settings. Therefore, careful consideration is needed to assess the practical applicability of asymptotic findings. Often, these are complemented by numerical simulations to validate the theoretical predictions for practically relevant parameter values.
LDNN Algorithm#
The LDNN (Linear Diagonal Neural Network) algorithm family, as analyzed in this paper, presents a novel approach to sparse recovery and feature learning. It elegantly combines the iteratively reweighted least-squares (IRLS) method with the Hadamard parameterization of weights. This reparameterization allows for a smooth, non-convex optimization landscape, which is addressed using a family of iterative algorithms including alternating minimization and lin-RFM. The key contribution lies in providing a precise, high-dimensional asymptotic analysis of this algorithm family under i.i.d. Gaussian covariates, revealing the algorithms’ convergence behavior and signal recovery capabilities. This rigorous analysis allows for a direct comparison between different algorithmic choices, including several variations of IRLS and a novel reweighting scheme, providing insights into the algorithms’ strengths and weaknesses. Furthermore, the analysis is extended to scenarios with group-sparse signals, demonstrating how leveraging group structure can significantly improve performance, achieving favorable error rates in only a few iterations.
Group-Sparse Gains#
The concept of ‘Group-Sparse Gains’ in the context of a high-dimensional linear model suggests that exploiting inherent group structures within sparse data can significantly improve model performance. This implies that instead of treating individual features independently, we should group correlated features together. This grouping leverages prior knowledge or observed relationships between variables, leading to a more efficient and accurate estimation of the underlying signal. A key benefit lies in the reduced complexity, as the model’s performance scales with the number of non-zero groups rather than the total number of individual features. The improvements stem from the ability of the model to efficiently identify and use relevant groups, effectively reducing the dimensionality of the problem. Algorithms designed to incorporate this group sparsity, such as grouped iteratively reweighted least squares (IRLS), likely demonstrate improved sample complexity and faster convergence compared to methods that ignore the inherent structure. Consequently, ‘Group-Sparse Gains’ highlights a strategy that combines efficient algorithmic approaches with informed feature engineering, resulting in better statistical performance and a clearer understanding of the underlying high-dimensional data. It emphasizes a move away from treating all dimensions equally towards using domain knowledge or model-learned structure to improve prediction accuracy and efficiency.
High-Dim Regime#
The high-dimensional regime, where the number of variables exceeds the number of observations, presents unique challenges in statistical analysis. Traditional methods often fail in this setting due to issues like overfitting. This research focuses on asymptotic analysis, studying algorithm behavior as the dimensionality grows. A key finding is the derivation of precise characterizations of algorithm iterates in the high-dimensional limit, enabling accurate prediction of test errors. The analysis also sheds light on the impact of algorithm choices and model architecture, such as the effectiveness of group-sparse reweighting and the number of iterations needed to reach favorable solutions. These insights are particularly valuable for understanding how to leverage structure in high-dimensional data for improved performance. The high-dimensional analysis goes beyond characterizing convergence and extends to providing quantifiable insights on the typical performance and sample efficiency of the algorithms, a significant improvement over existing theoretical analyses which frequently rely on worst-case scenarios.
Future Extensions#
Future research could explore several promising avenues. Extending the theoretical analysis to non-batched settings would remove the current limitation of requiring independent data batches at each iteration. This would make the framework applicable to a wider range of real-world scenarios. Investigating the impact of different initialization strategies on algorithm performance would provide a more comprehensive understanding of the algorithm’s behavior. Furthermore, analyzing the algorithm’s robustness to various noise models beyond i.i.d. Gaussian noise would enhance the practical applicability of the findings. Finally, exploring alternative reweighting schemes and their theoretical implications could lead to the discovery of even more efficient and robust algorithms for training linear diagonal networks.
More visual insights#
More on figures
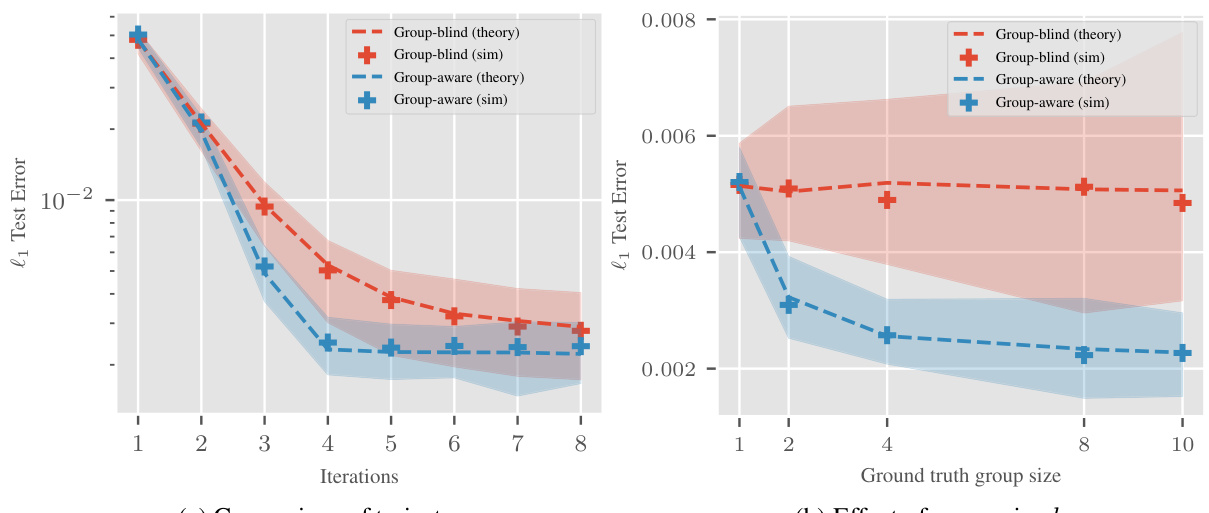
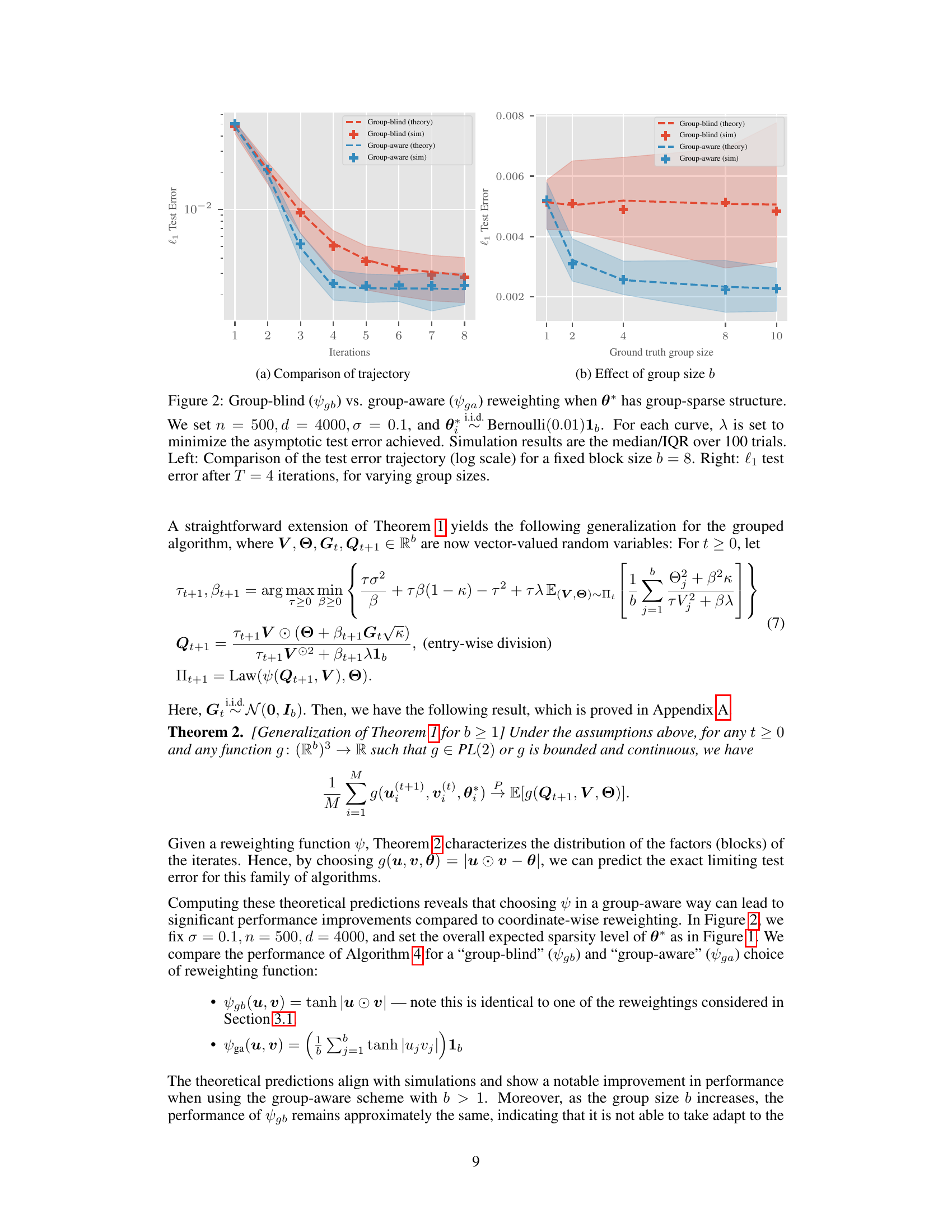
This figure compares the performance of group-blind and group-aware reweighting schemes for learning linear diagonal networks when the underlying signal has a group-sparse structure. The left panel shows the test error trajectory (log scale) over eight iterations for a fixed block size (b=8). The right panel shows the test error after four iterations for various group sizes (b). The results demonstrate that a group-aware reweighting scheme significantly outperforms a group-blind approach, particularly as the group size increases.

This figure compares theoretical predictions and experimental simulations of the l1 test error and mean squared error for different reweighting functions. It showcases the accuracy of the theoretical predictions, even when the reweighting functions don’t meet the strict assumptions of the theoretical analysis (for example, the functions are not uniformly bounded). The plots show the median error and interquartile range over 100 trials.
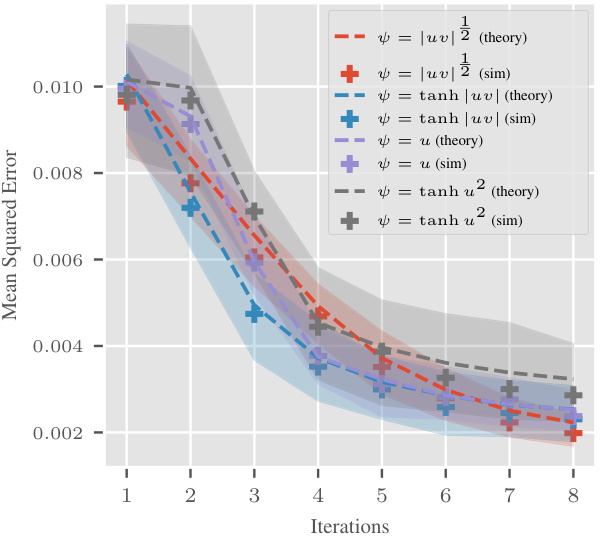
This figure compares theoretical predictions and simulation results for the mean squared error of different reweighting functions in high-dimensional sparse linear regression. The left panel focuses on reweighting functions that are not uniformly bounded, while the right panel shows results for the squared error. The results show a close match between theoretical predictions and simulations across various reweighting schemes and demonstrate that even without uniformly bounded reweighting functions the model yields accurate results. The test error is low after only a few iterations across all considered weightings.
Full paper#