↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Estimating the 3D orientation of objects in images (single-image pose estimation) is crucial in many applications. Current methods often use Euler angles or quaternions to represent 3D rotations, but these representations can have discontinuities and singularities, hindering performance. SO(3)-equivariant networks offer a structured way to capture pose patterns, but their use with spherical CNNs (which operate in the frequency domain for efficiency) has been limited by incompatible spatial domain parameterizations.
This paper introduces a frequency-domain approach that directly predicts Wigner-D coefficients for 3D rotation regression. This aligns with the operations of spherical CNNs, avoiding issues of spatial representations. Using a frequency-domain regression loss, the SO(3)-equivariant pose harmonics predictor achieves state-of-the-art results on ModelNet10-SO(3) and PASCAL3D+, showing significant improvements in accuracy, robustness, and data efficiency. The method bypasses limitations of spatial parameterizations, ensuring consistent pose estimation under arbitrary rotations.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and efficient approach to 3D pose estimation, addressing limitations of existing methods. Its SO(3)-equivariant network, operating in the frequency domain, enhances accuracy, robustness, and data efficiency. This work is relevant to various research areas, including augmented reality, robotics, and autonomous vehicles, and opens new avenues for research in SO(3)-equivariant networks and probabilistic pose estimation.
Visual Insights#
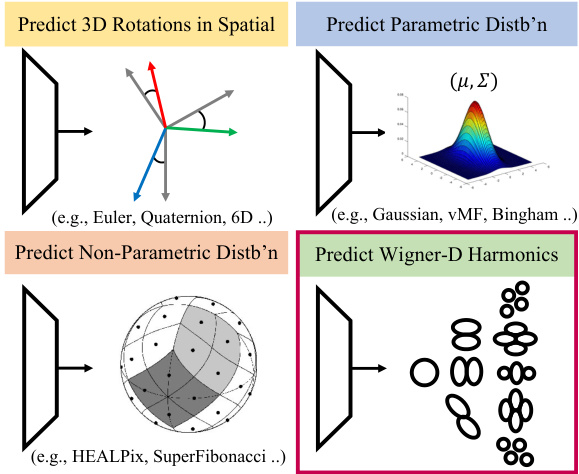
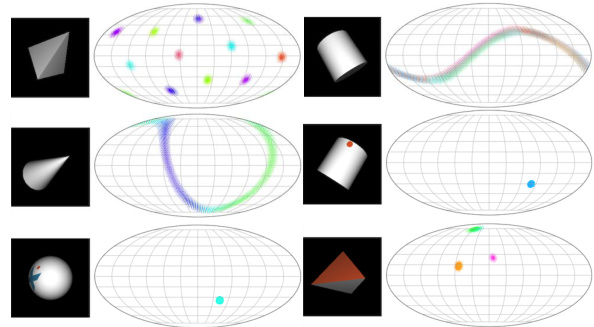
This figure illustrates four different ways to represent 3D rotations, comparing spatial-domain methods with frequency-domain methods. The spatial-domain methods include predicting the rotation parameters directly (e.g., Euler angles, quaternions, or 6D representations), or predicting a parametric distribution of rotations (e.g., Gaussian, von Mises-Fisher, or Bingham distributions). The frequency-domain method, shown as the preferred method in this paper, involves predicting the Wigner-D harmonics, which are coefficients representing the rotation in the frequency domain. The figure highlights the advantage of the Wigner-D harmonic approach for continuous representation of rotations, avoiding the discontinuities and singularities present in spatial-domain methods.
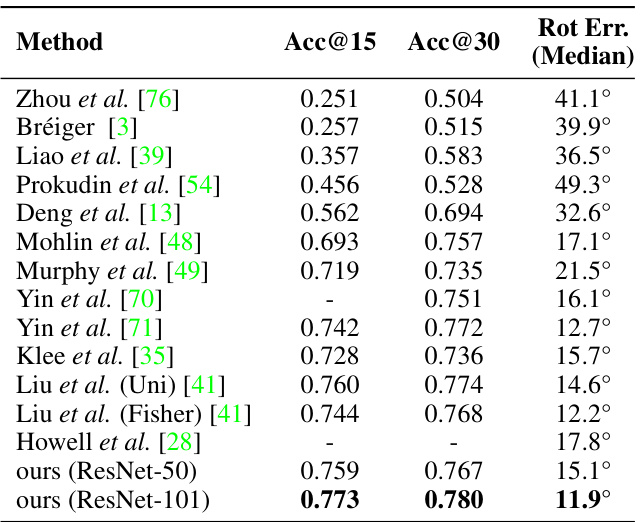
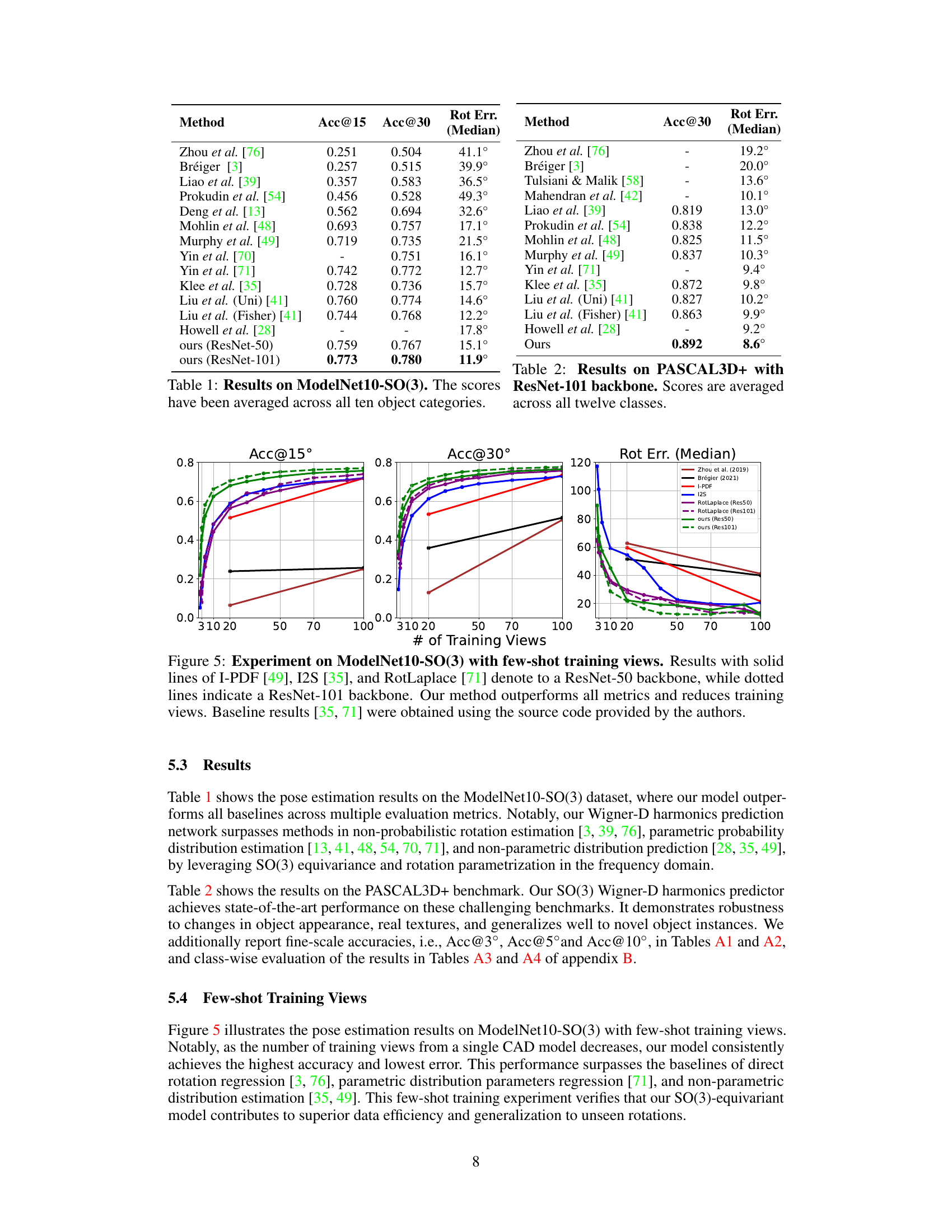
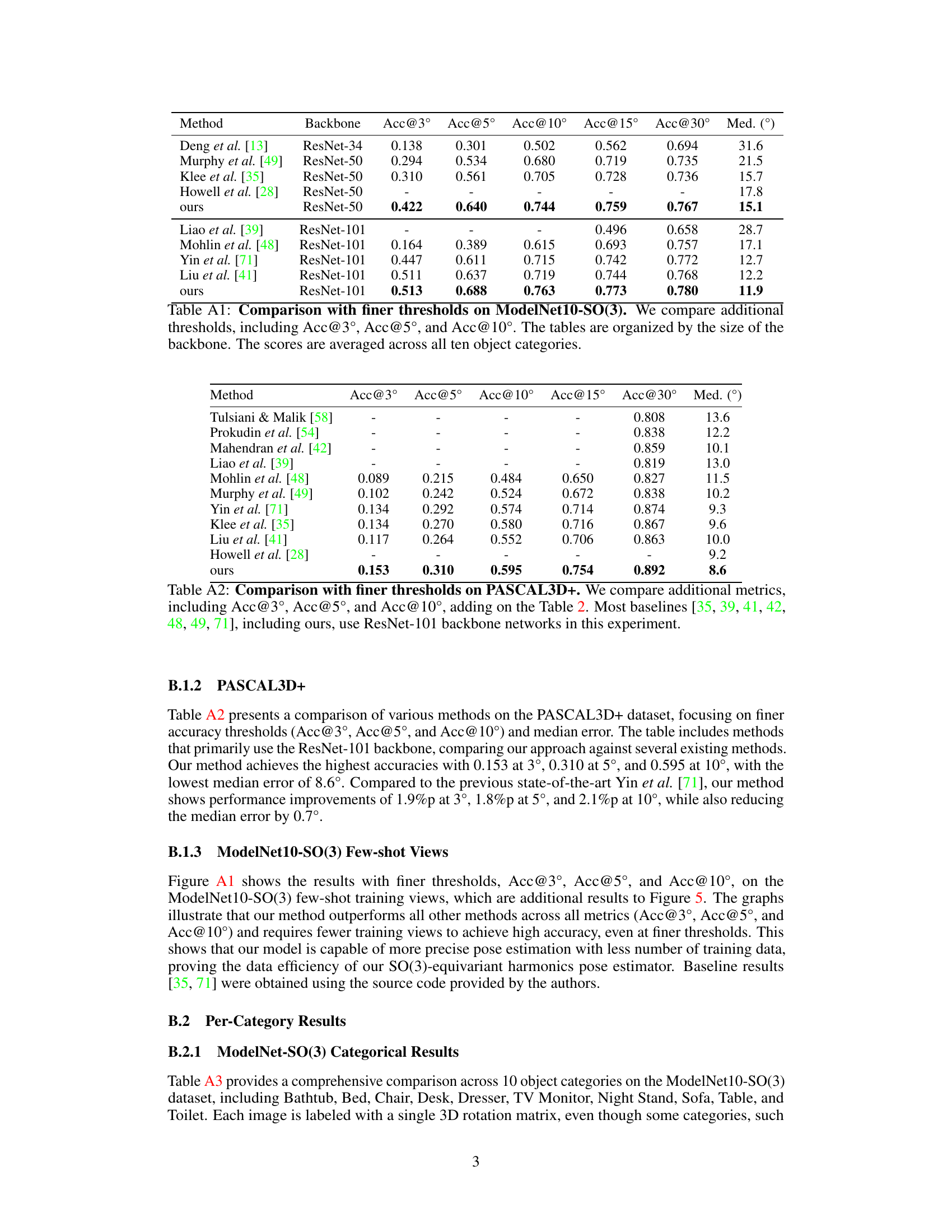
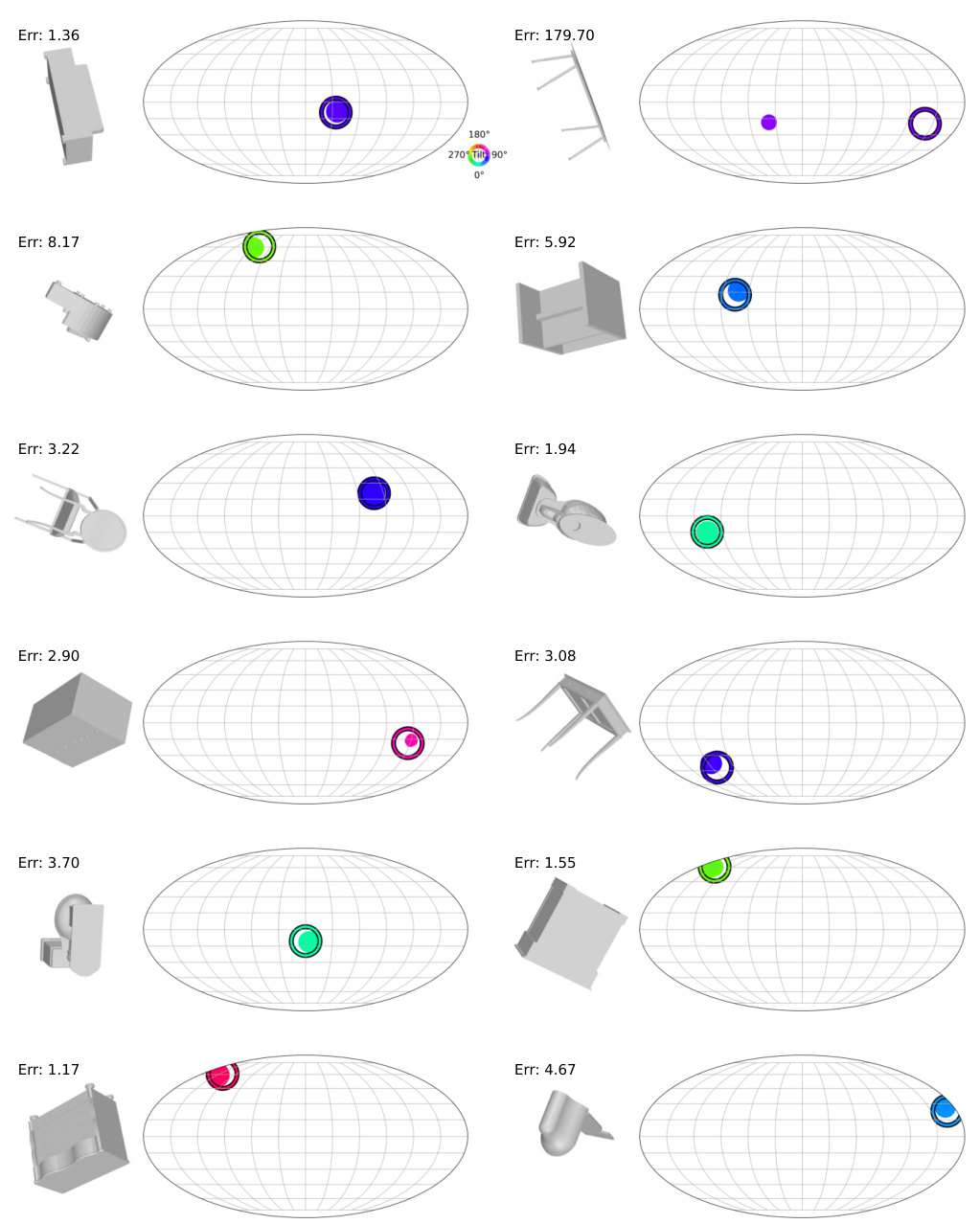
This table presents the quantitative results of the proposed method on the ModelNet10-SO(3) benchmark dataset. It compares the performance of the proposed method against various state-of-the-art methods. The metrics used are Acc@15 (accuracy within 15 degrees of error), Acc@30 (accuracy within 30 degrees of error), and median rotation error. The results show that the proposed method achieves better performance in all three metrics, demonstrating its effectiveness compared to other techniques in 3D pose estimation.
In-depth insights#
SO(3) Equivariance#
SO(3) equivariance is a crucial concept in the paper, signifying the network’s ability to maintain consistent outputs under arbitrary 3D rotations of the input. This inherent rotational consistency is achieved by directly predicting Wigner-D coefficients in the frequency domain, aligning with the operations of spherical CNNs. Unlike spatial-domain parameterizations (Euler angles, quaternions), which suffer from discontinuities and singularities, this frequency-domain approach ensures smooth and continuous pose estimation. The SO(3) equivariance guarantees that rotating the input will predictably rotate the output by the same amount, enhancing accuracy, robustness and generalizability, particularly to unseen rotations. This property is fundamental to the success of the proposed model, highlighting its superiority over existing methods that lack this critical feature.
Wigner-D Regression#
Wigner-D regression, in the context of 3D pose estimation, offers a novel approach by directly regressing Wigner-D coefficients, which represent rotations in the frequency domain. This technique avoids the limitations of spatial-domain representations like Euler angles or quaternions, which suffer from discontinuities and singularities. The frequency-domain approach aligns well with spherical CNNs, enhancing computational efficiency and SO(3) equivariance. Direct regression of Wigner-D coefficients ensures consistent pose estimation under arbitrary rotations, unlike spatial methods. This approach leads to improved accuracy, robustness, and potentially greater data efficiency compared to existing methods, as evidenced by the state-of-the-art results reported in various benchmark datasets. However, challenges still remain in handling pose ambiguity for highly symmetric objects and managing the computational cost associated with high-frequency Wigner-D coefficients. Further research could focus on incorporating methods to handle uncertainty and improving computational efficiency.
Frequency-Domain Loss#
The concept of a ‘Frequency-Domain Loss’ in the context of 3D rotation estimation is quite innovative. Traditional methods often parameterize rotations in the spatial domain (Euler angles, quaternions), leading to discontinuities and singularities that hinder optimization. By operating directly in the frequency domain using Wigner-D harmonics, the proposed method avoids these pitfalls. The loss function, therefore, would measure the difference between predicted and ground truth Wigner-D coefficients. This approach not only leverages the strengths of spherical CNNs which naturally operate in the frequency domain but also ensures rotational consistency. The frequency-domain loss is expected to be more robust and lead to more accurate and stable 3D rotation estimates. The choice of loss function (e.g., MSE) should carefully consider the properties of the Wigner-D coefficients, possibly weighting different harmonic frequencies differently to prioritize certain aspects of the rotation.This approach is a significant departure from existing spatial-domain methods and promises enhanced accuracy and data efficiency.
Few-Shot Learning#
Few-shot learning tackles the challenge of training machine learning models with limited data. Traditional deep learning approaches require massive datasets, a constraint often unmet in specialized domains. Few-shot learning aims to enable models to generalize effectively from just a handful of examples per class, drastically reducing the data demands. This is achieved through various techniques such as meta-learning, where models learn to learn by training on multiple tasks, and data augmentation, where existing data is cleverly modified to increase its apparent volume. Successful few-shot learning hinges on the ability of the model to effectively extract and utilize relevant features, generalizing beyond the few examples provided during training. This paradigm is particularly valuable in situations with data scarcity, high annotation costs, or rapidly evolving environments, making it a significant area of research with vast potential implications for many applications.
Pose Distribution#
The concept of “Pose Distribution” in 3D object pose estimation is crucial for handling uncertainty and ambiguity inherent in real-world scenarios. Instead of predicting a single pose, modeling pose as a distribution acknowledges the inherent variability in object orientations, especially with symmetries or when viewed from less-informative perspectives. This approach yields a more robust and accurate estimation, particularly under noisy or incomplete data. The choice of distribution (e.g., von Mises-Fisher, Bingham, matrix Fisher) plays a significant role in capturing the characteristics of the rotational uncertainty. The use of non-parametric methods allows for more flexible modeling of complex, multi-modal pose distributions, overcoming the limitations of predefined parametric forms. Further research could explore combining parametric and non-parametric approaches for optimal accuracy and efficiency. Finally, effective representation and manipulation of pose distributions are essential for training and inference, impacting algorithm performance and interpretability.
More visual insights#
More on figures
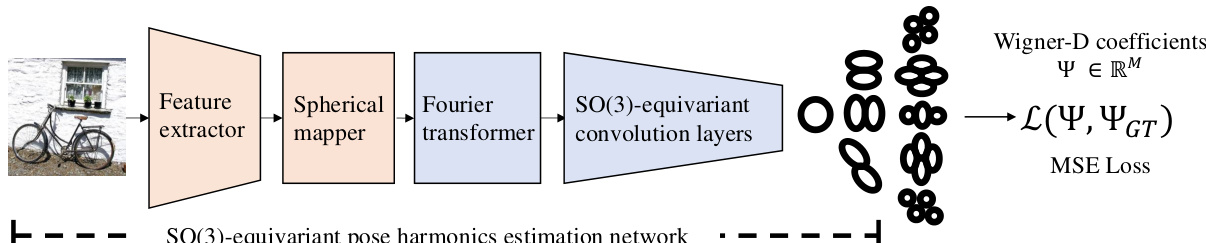
The figure illustrates the architecture of the SO(3)-equivariant pose harmonics estimation network. It starts with a feature extractor (using a pre-trained ResNet), followed by a spherical mapper that projects the features onto a sphere, a Fourier transformer to convert to the frequency domain, and finally SO(3)-equivariant convolutional layers. The output is a set of Wigner-D coefficients (Ψ) representing the 3D rotation, which are then compared to ground truth using an MSE loss.
This figure illustrates the architecture of the SO(3)-equivariant pose harmonics regression network. It shows the four main components: feature extraction (using a pre-trained ResNet), spherical mapping (projecting the features onto a sphere), Fourier transformation (converting to the frequency domain), and SO(3)-equivariant convolutional layers. The output is a set of Wigner-D coefficients representing the 3D rotation.

The figure illustrates the architecture of the SO(3)-equivariant pose harmonics regression network. It details the four main stages: feature extraction (using a pre-trained ResNet), spherical mapping (projecting features onto a sphere), Fourier transformation (converting to frequency domain), and SO(3)-equivariant convolutional layers (processing in the frequency domain). The final output is a set of Wigner-D harmonics coefficients representing the 3D rotation.

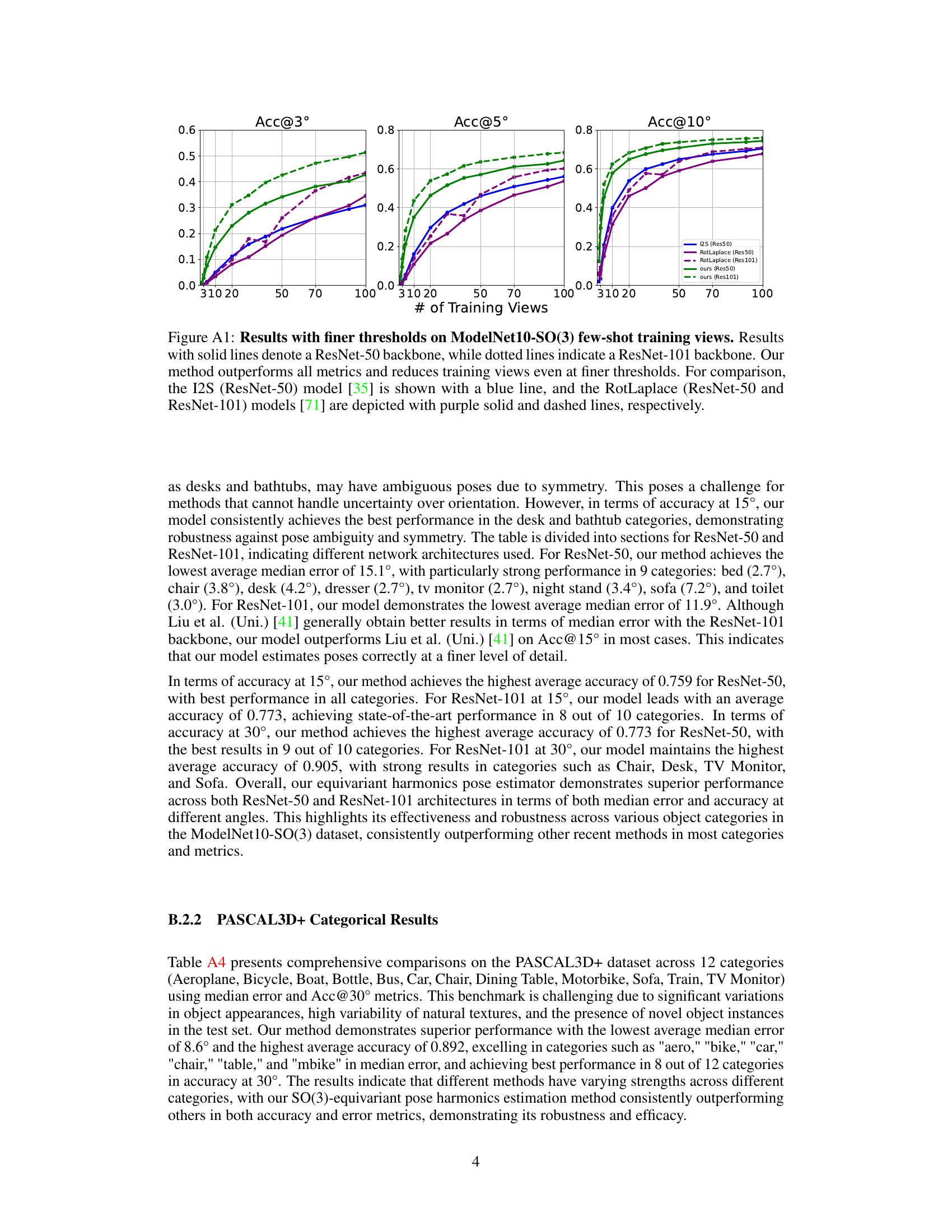
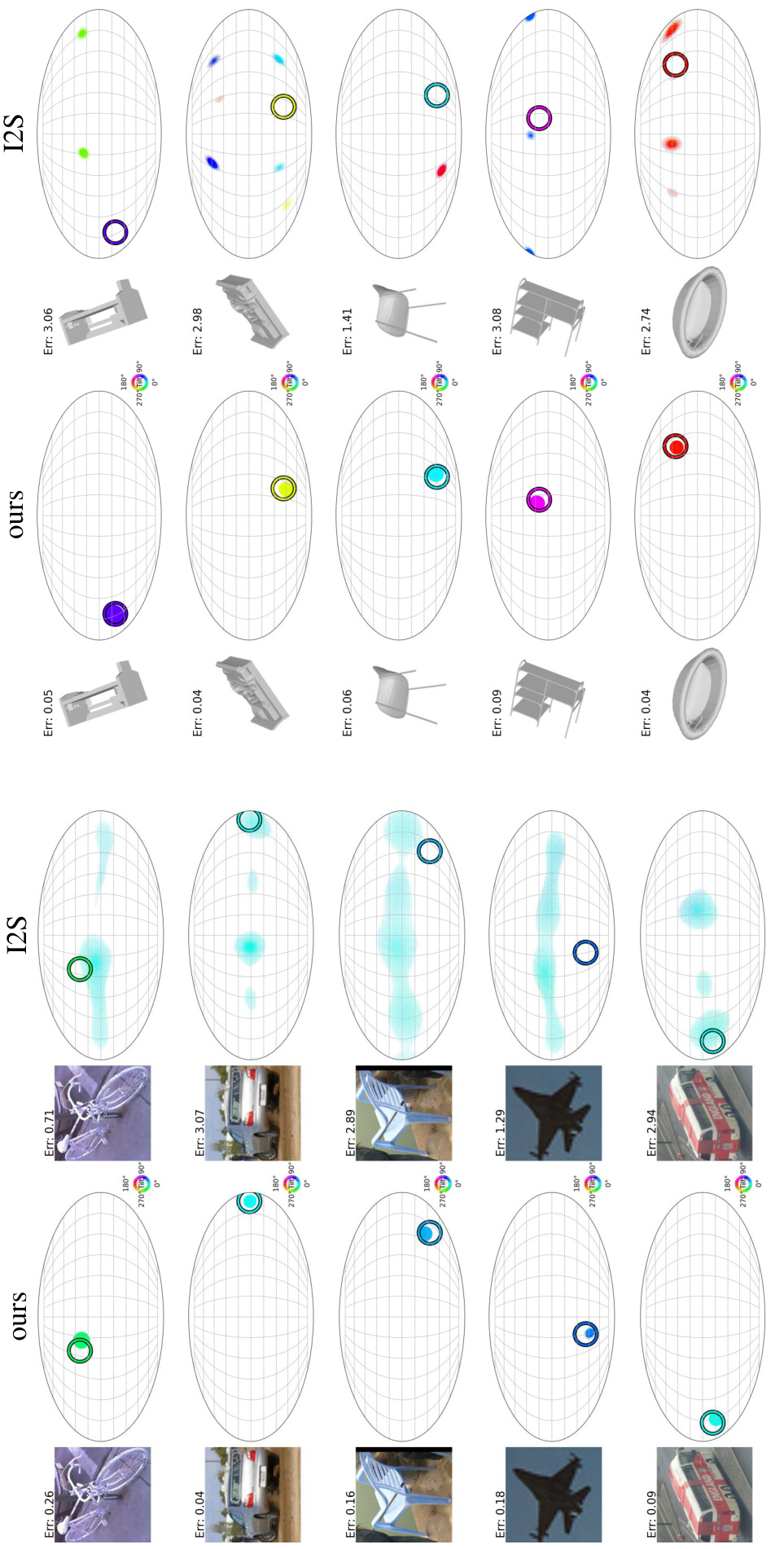
This figure shows the results of an experiment on the ModelNet10-SO(3) dataset with varying numbers of training views. The experiment compares the performance of different methods (I-PDF, I2S, RotLaplace, and the proposed method) in estimating 3D rotations using ResNet-50 and ResNet-101 backbones. The plot shows the accuracy (Acc@15°, Acc@30°) and median rotation error for different numbers of training views. The results demonstrate that the proposed method outperforms other methods across all metrics and requires fewer training views.
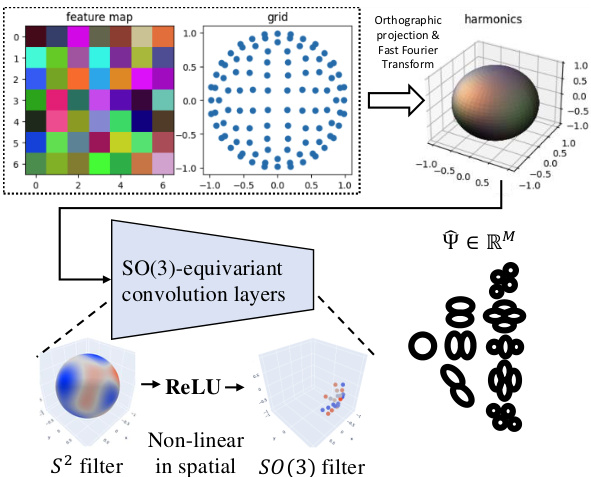
This figure illustrates the architecture of the SO(3)-equivariant pose harmonics prediction network. It consists of four main parts: a feature extractor (using a pre-trained ResNet), a spherical mapper (projecting features onto a sphere), a Fourier transformer (converting to the frequency domain), and SO(3)-equivariant convolution layers. The network directly predicts the Wigner-D harmonics coefficients, representing 3D rotations, for efficient and continuous pose estimation.
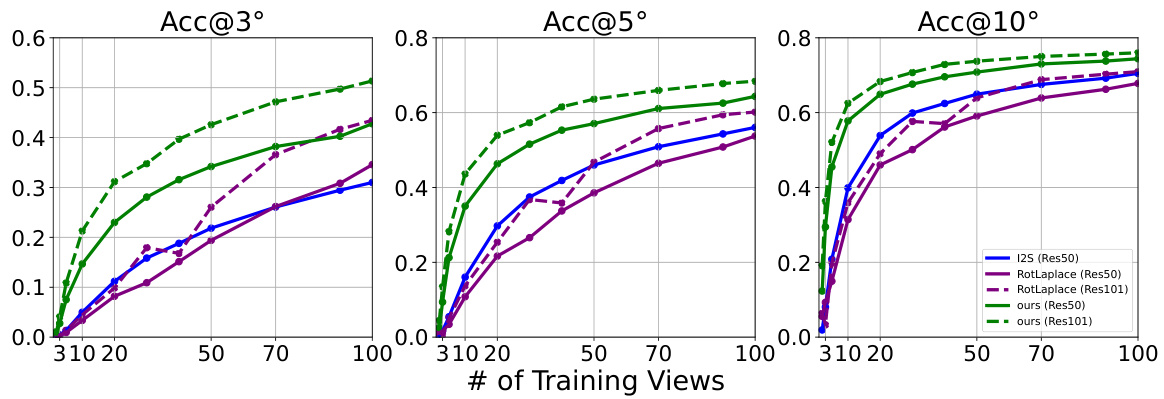
This figure shows the performance comparison of different methods on the ModelNet10-SO(3) dataset with varying numbers of training views. The x-axis represents the number of training views per object, and the y-axis represents the accuracy at different angular error thresholds (3°, 5°, and 10°). The results demonstrate that the proposed method outperforms existing state-of-the-art methods across all metrics and requires fewer training views to achieve high accuracy.
This figure illustrates the architecture of the SO(3)-equivariant pose harmonics prediction network. It shows the four main components: feature extraction (using a pre-trained ResNet), spherical mapping (projecting features onto a sphere), Fourier transformation (converting to the frequency domain), and SO(3)-equivariant convolutional layers. The output is the Wigner-D coefficients, representing the 3D rotation.

This figure illustrates the overall architecture of the proposed SO(3)-equivariant pose harmonics prediction network. It shows the four main components: a feature extractor (pre-trained ResNet), a spherical mapper (projects features onto a sphere), a Fourier transformer (converts spatial to frequency domain), and SO(3)-equivariant convolution layers. The output is the Wigner-D harmonics coefficients, representing 3D rotations.
The figure illustrates the architecture of the SO(3)-equivariant pose harmonics prediction network. The network comprises four stages: feature extraction using a pre-trained ResNet, a spherical mapper that projects the features onto a sphere, a Fourier transformer that converts the data to the frequency domain, and SO(3)-equivariant convolutional layers that perform the pose estimation. The output is a set of Wigner-D coefficients representing the 3D rotation.
More on tables
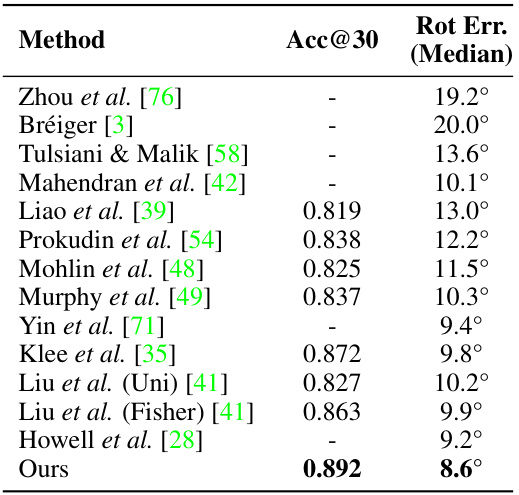
This table presents the results of the proposed method and several baseline methods on the ModelNet10-SO(3) dataset. The table shows the accuracy at 15° and 30° thresholds (Acc@15, Acc@30), and the median rotation error (Rot Err. (Median)). The results are averaged across all ten object categories in the dataset. It demonstrates the superior performance of the proposed method compared to existing approaches in terms of pose estimation accuracy.

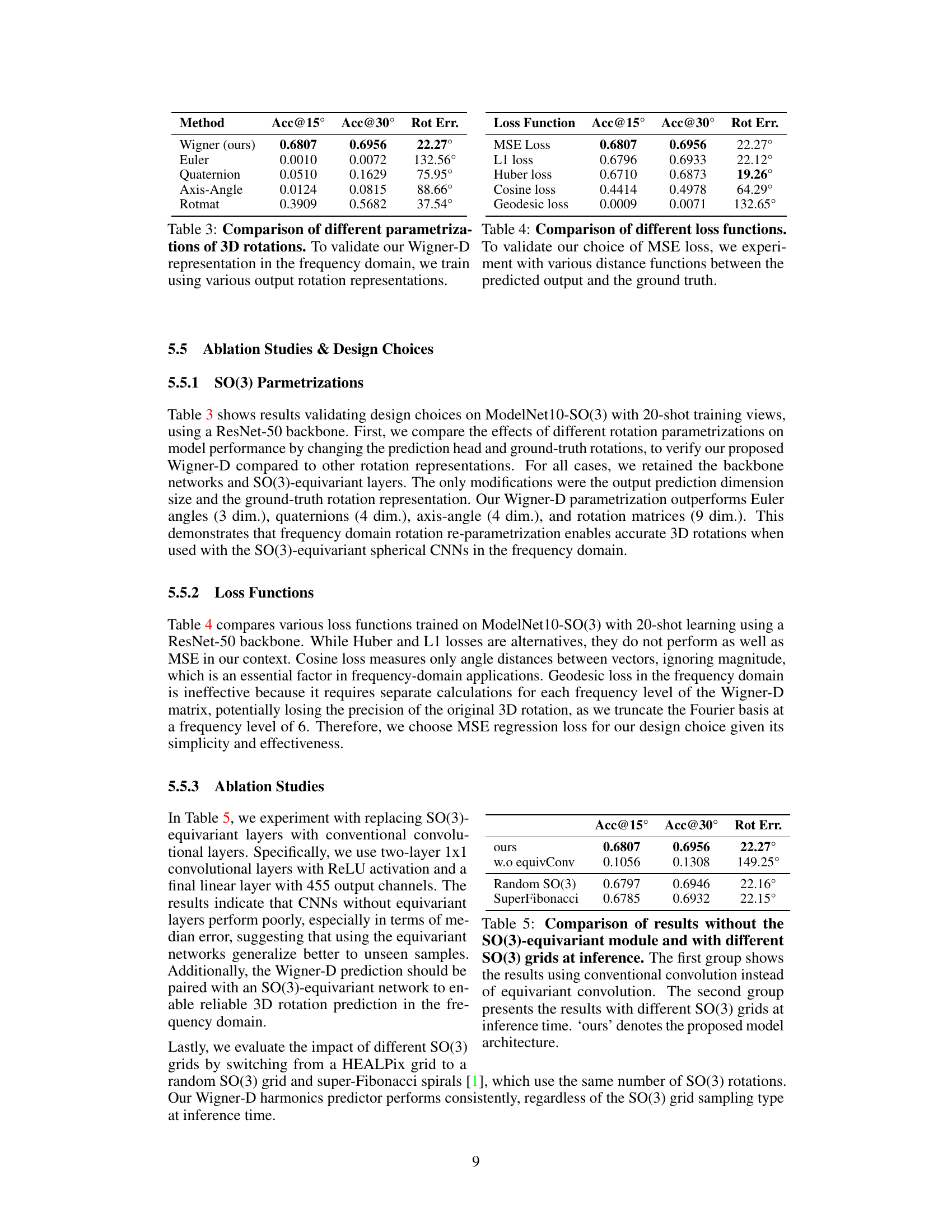
This table compares the performance of different 3D rotation representations (Wigner, Euler angles, Quaternions, Axis-Angle, and Rotation matrices) used in the pose estimation model. The goal is to demonstrate the superiority of using Wigner-D coefficients as the model’s output, which is central to the paper’s approach. The table shows that Wigner-D significantly outperforms other representations in terms of Acc@15°, Acc@30°, and median rotation error. This highlights the advantage of the frequency domain representation for accurate 3D pose estimation.
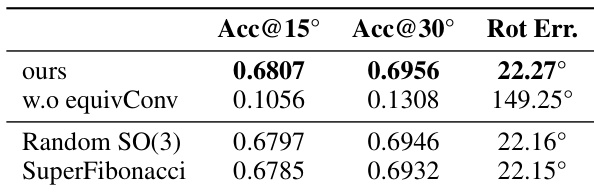
This table presents ablation study results focusing on two key aspects of the proposed model: the SO(3)-equivariant convolutional layers and the SO(3) grid used during inference. The first part compares the performance of the model with and without SO(3)-equivariant layers, highlighting the significant contribution of these layers to the overall accuracy. The second part investigates the impact of using different SO(3) grid sampling methods (random SO(3) and SuperFibonacci) on the model’s performance, showing that while performance varies slightly the proposed method remains consistently strong.

This table presents a comparison of the average log-likelihood scores achieved by three different training methods on the SYMSOL I and II datasets. The three methods are: 1. Using only the Wigner-D regression loss (Lwigner). 2. Using only the distribution loss from the I-PDF method (Ldist), which is the same as the results from the I2S method. 3. Jointly training the model with both the Wigner-D regression loss and the distribution loss (Lwigner + Ldist). The results show that joint training achieves the best performance for most object categories in both SYMSOL I and SYMSOL II.
This table compares the performance of different 3D rotation parameterizations (Wigner-D, Euler angles, quaternions, axis-angle, and rotation matrices) used in the proposed method. The results demonstrate the superiority of the Wigner-D representation for accurate 3D rotation prediction when used with SO(3)-equivariant networks in the frequency domain.

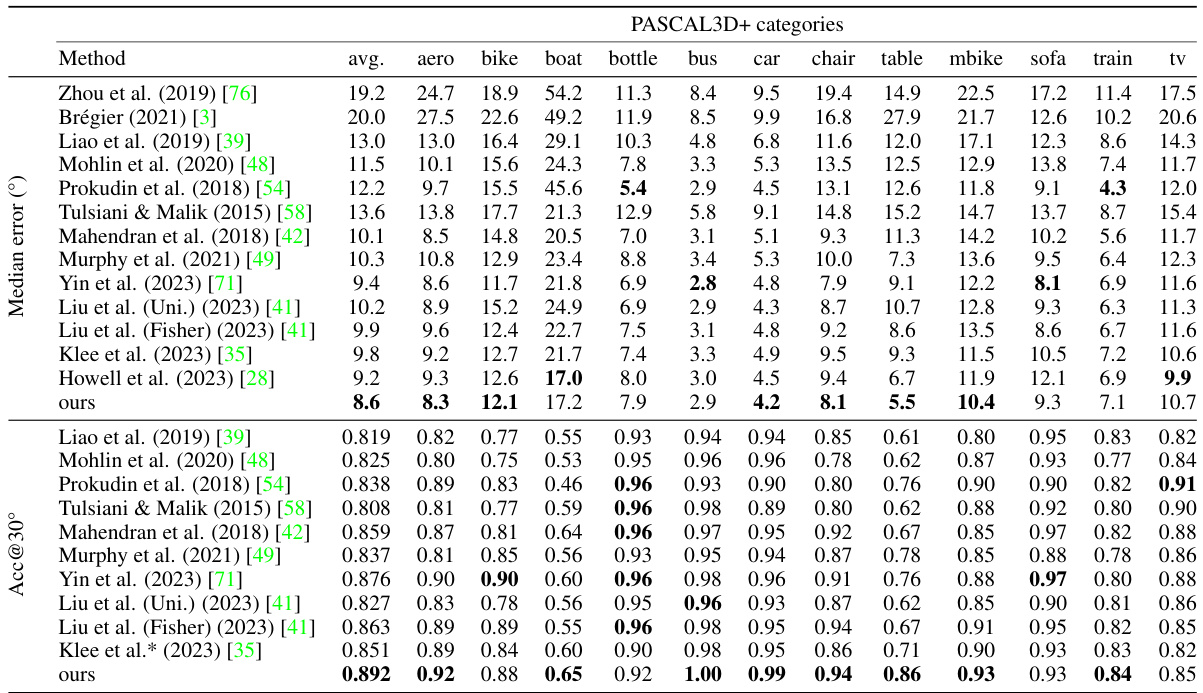
This table presents the results of the proposed method on the PASCAL3D+ benchmark dataset. The ResNet-101 architecture was used as the backbone. The results show the accuracy at 15 and 30 degrees error thresholds (Acc@15°, Acc@30°), along with the median rotation error (Median). The scores shown are averaged across all 12 object categories in the dataset.

This table presents the results of the proposed method and several baseline methods on the ModelNet10-SO(3) dataset. It shows the accuracy (Acc@15°, Acc@30°) and median rotation error for each method, averaged across all ten object categories in the dataset. The results demonstrate the performance of different approaches to 3D rotation estimation.
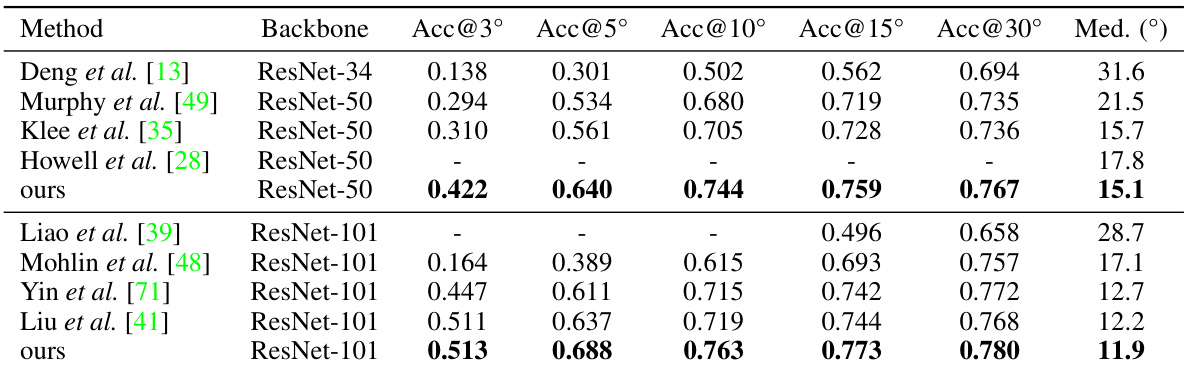
This table compares the performance of different methods on the PASCAL3D+ dataset using finer accuracy thresholds (Acc@3°, Acc@5°, Acc@10°) and median error. The methods primarily utilize the ResNet-101 backbone architecture. The table highlights our method’s superior performance compared to existing techniques in achieving the highest accuracies and lowest median error across these metrics.

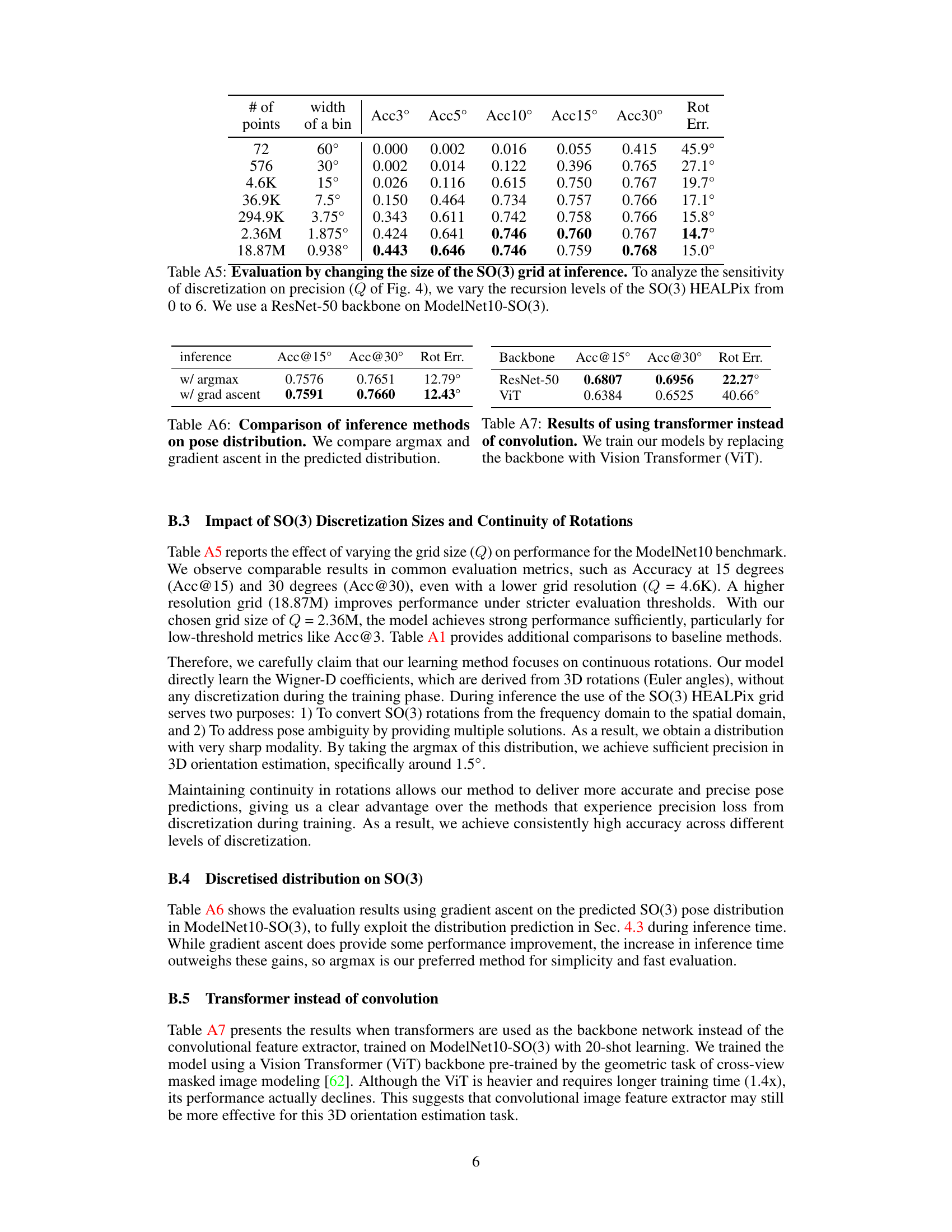
This table presents the results of an experiment conducted to evaluate the impact of varying the SO(3) grid size at inference time on the accuracy of the pose estimation. The experiment involved varying the recursion levels of the SO(3) HEALPix grid (Q in Figure 4) from 0 to 6, while using a ResNet-50 backbone on ModelNet10-SO(3). The results are presented in terms of accuracy at different thresholds (Acc3°, Acc5°, Acc10°, Acc15°, Acc30°) and the median rotation error (Rot Err.). The findings indicate the effect of different discretization levels on the precision of the pose estimation.

This table compares two inference methods, argmax and gradient ascent, used to determine the final 3D rotation from a predicted distribution of rotations. The results show that the gradient ascent method achieves slightly better accuracy in terms of Acc@15°, Acc@30°, and median rotation error. However, the differences are small, suggesting that the argmax method might be a computationally faster and simpler choice for inference.

This table shows the impact of varying the maximum frequency level L on the accuracy of pose prediction using SO(3) group convolutions. The results indicate that increasing L up to 5 consistently improves accuracy metrics, but beyond that point, adding more frequencies leads to decreased performance, possibly due to overfitting to noise.
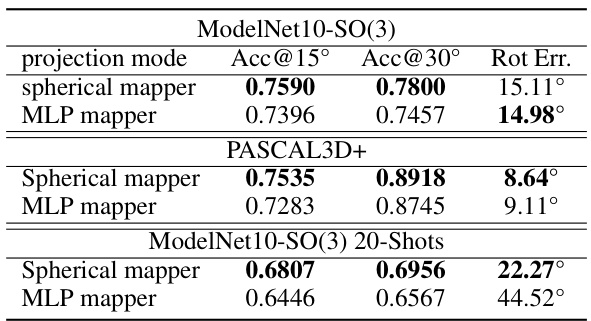
This table compares the performance of two different projection methods: spherical mapper and MLP mapper, in terms of accuracy and rotation error on ModelNet10-SO(3) and PASCAL3D+ datasets. The spherical mapper, which projects image features onto a sphere, outperforms the MLP mapper, which directly maps features to harmonics. This highlights the effectiveness of the spherical mapper in preserving spatial information and geometric properties, crucial for accurate pose estimation.
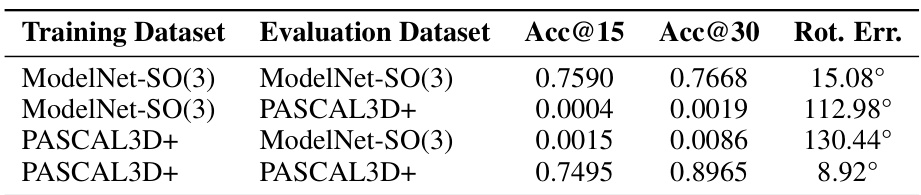
This table presents the results of a cross-dataset evaluation to assess the model’s ability to generalize to unseen data. The model, trained on either ModelNet10-SO(3) or PASCAL3D+, is evaluated on both datasets. The results show the accuracy (Acc@15 and Acc@30) and median rotation error (Rot. Err.) for each training-evaluation dataset combination. This helps to understand how well the model generalizes beyond the specific dataset it was trained on.

This table compares the inference time and GPU memory usage of four different methods for 3D pose estimation: our proposed method, and three baseline methods. The comparison is performed on the ModelNet10-SO(3) test set using a machine with an Intel i7-8700 CPU and an NVIDIA GeForce RTX 3090 GPU. The results show that our method achieves the fastest inference time, but at the cost of higher GPU memory consumption.
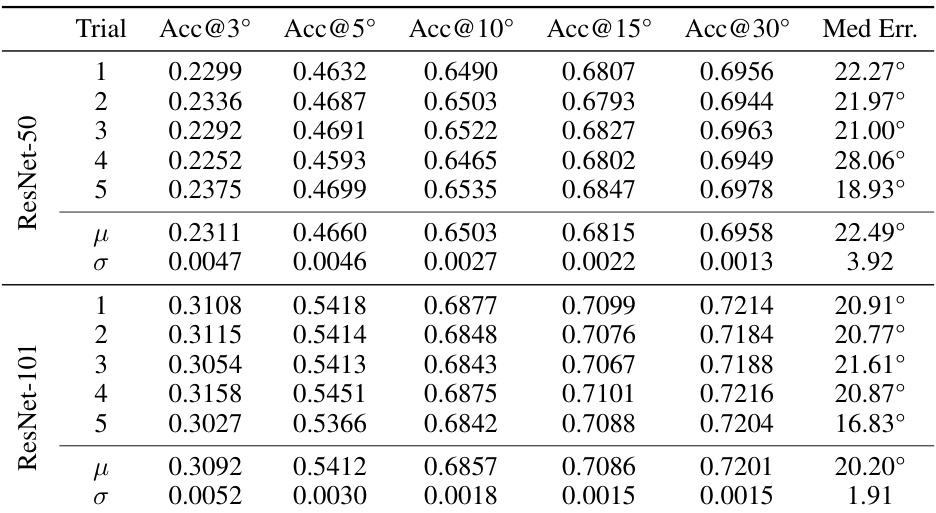
This table shows the results of five independent training runs for both ResNet-50 and ResNet-101 backbones on the ModelNet10-SO(3) dataset. It demonstrates the stability and reproducibility of the training process by showing the mean (μ) and standard deviation (σ) for several metrics, indicating how much the results vary across different runs. The low standard deviation values confirm the consistency of the model’s performance.
Full paper#