TL;DR#
Large-scale scientific simulations generate massive floating-point datasets, demanding efficient compression. Existing methods, while effective for general data, underperform on scientific data due to noise and high-order information stemming from model inaccuracies and discretization. These methods fail to exploit the underlying mechanisms of data generation.
MeLLoC (Mechanism Learning for Lossless Compression) tackles this problem by learning the high-order mechanisms within scientific data. It treats data as samples from an underlying physical field governed by differential equations and identifies the governing equations to obtain a more compressible representation. This innovative approach, combined with periodic extension techniques for faster decompression, consistently surpasses current state-of-the-art lossless compressors. The method successfully balances high compression ratios and efficient computational performance across different scientific datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel lossless compression method, MeLLoC, specifically designed for scientific floating-point data. This is a significant contribution because existing methods often struggle with the unique characteristics of this type of data, such as noise and high-order information. MeLLoC’s ability to significantly improve compression ratios while maintaining computational efficiency has important implications for various fields that rely on large-scale scientific datasets. The method also opens new avenues for leveraging domain knowledge and high-order information to improve data compression techniques.
Visual Insights#

🔼 This figure illustrates the MeLLoC framework’s architecture. It starts with the original data which undergoes a local mechanism analysis represented by solving the equation Kcuin = bubd,f. The results are then separated into boundary data (ubd) and source term (f). A precision control step optimizes these components before encoding and decoding, which ultimately leads to reconstructed data that closely matches the original data. The figure visually showcases the key stages of the compression process: learning a local mechanism from data, separating boundary and source term, utilizing precision control and applying encoding and decoding.
read the caption
Figure 1: Overview of the proposed compression architecture.
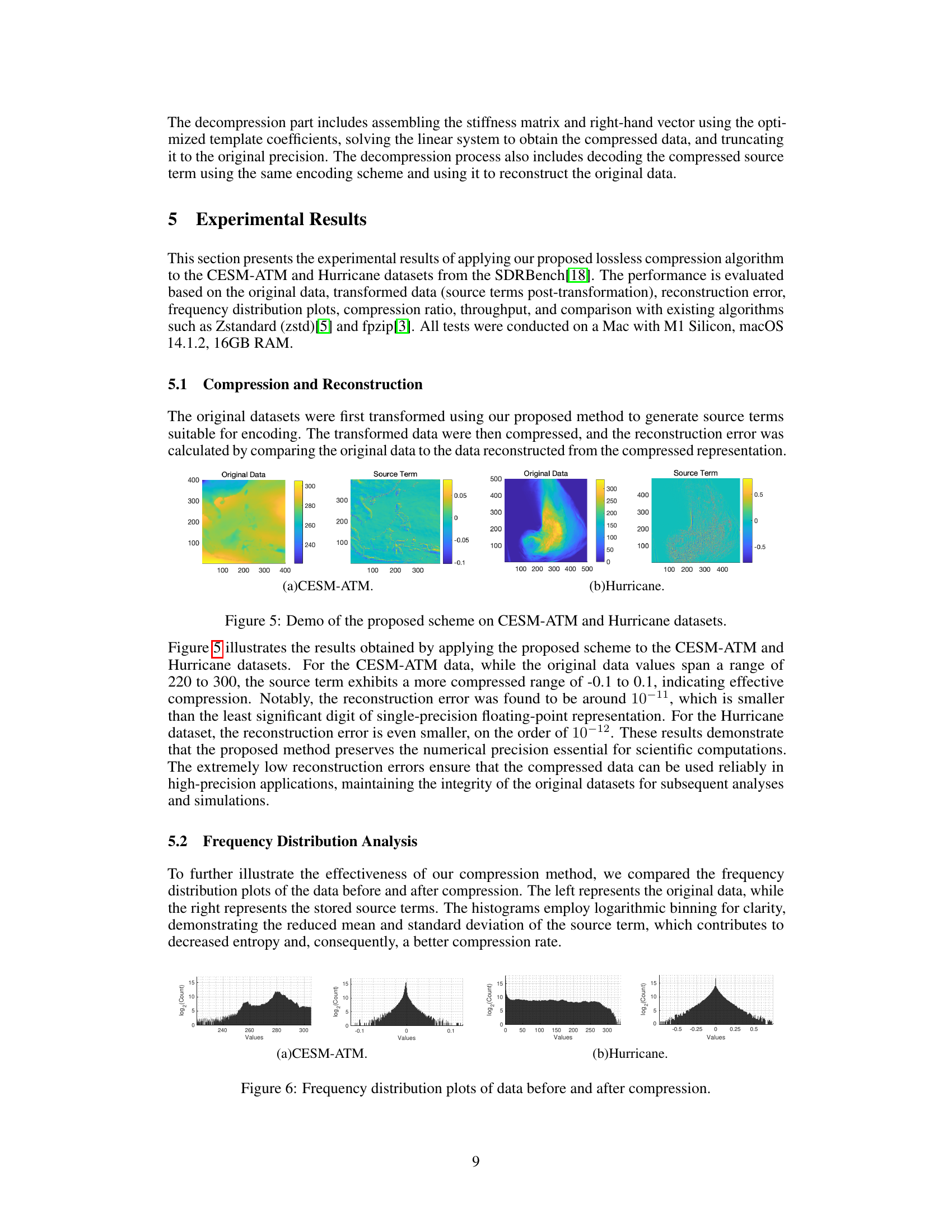
🔼 This table compares the performance of MeLLoC against several state-of-the-art compression algorithms (ALP, FPZIP, ZFP, Blosc, Gzip, Zstandard) using two key metrics: compression ratio and throughput. The compression ratio indicates the efficiency of data reduction, with higher values representing more compact representations. Throughput measures the speed of compression and decompression processes, which is crucial for handling large scientific datasets. The comparison is done on two datasets: CESM-ATM and Hurricane.
read the caption
Table 1: Performance comparison.
In-depth insights#
PDE-based Compression#
PDE-based compression leverages the inherent structure of scientific data, often modeled by partial differential equations (PDEs), to achieve higher compression ratios than traditional methods. The core idea is to identify the underlying PDE governing the data and then represent the data using a smaller set of parameters describing the PDE’s solution, rather than storing the entire dataset. This approach is particularly effective for data exhibiting smooth, continuous behavior characteristic of physical phenomena modeled by PDEs. However, challenges exist in efficiently identifying the correct PDE from noisy, discrete samples and accurately solving the inverse problem. Furthermore, the computational cost of solving PDEs can be substantial, especially for large datasets, potentially offsetting the gains in storage efficiency. The success of PDE-based compression hinges on the balance between finding an effective representation and managing computational resources. Identifying efficient numerical solvers is crucial. The technique is best suited for data arising from simulations and experiments governed by known or readily identifiable PDEs, making it a domain-specific compression method rather than a general-purpose one.
Mechanism Learning#
The core of the proposed MeLLoC framework lies in its innovative use of mechanism learning to enhance lossless compression of scientific data. Instead of treating the data as mere numbers, MeLLoC recognizes the underlying physical processes often described by differential equations. By modeling these mechanisms, the method aims to identify the governing equations and their parameters. This approach is significant because it moves beyond treating data as a random collection of numbers and allows the algorithm to exploit the intrinsic structure and relationships within the data. This inherent structure is often more compressible than the raw data itself, leading to better compression ratios. However, the success of this approach hinges on accurate identification of these underlying mechanisms. This requires careful consideration of the PDEs which describe the data generation processes as well as robust methods for solving the inverse problem to recover the model parameters. The computational complexity of solving these equations is another critical factor that must be addressed to ensure efficiency.
Precision Control#
The heading ‘Precision Control’ highlights a critical aspect of the proposed MeLLoC compression method. It addresses the challenge of balancing compression efficiency with data fidelity by carefully managing the precision of the learned model parameters and the source term. The core idea is to determine an optimal level of precision for the source term that minimizes its size without compromising the accuracy of the reconstructed data. This involves a trade-off: high precision leads to more accurate reconstruction but larger source term sizes, while lower precision reduces the size but might increase reconstruction error. MeLLoC strategically addresses this by iteratively adjusting the precision, ensuring that the reconstruction error stays below a predefined threshold. This dynamic control mechanism allows MeLLoC to adapt to various scientific datasets, achieving optimal compression ratios while maintaining the integrity of the original data. The implementation details of this precision control are crucial for MeLLoC’s success, highlighting the sophistication involved in balancing compression efficiency with the demands of accuracy inherent in scientific computing applications.
High-Order Effects#
The concept of “High-Order Effects” in scientific data compression addresses the limitations of methods that only capture low-order information. High-order effects represent phenomena not adequately described by simple, low-order models, arising from complexities in physical systems or numerical approximations. These might include subtle variations, intricate interactions, or fine-scale details often lost in traditional compression schemes. Addressing high-order effects can significantly improve compression rates by identifying and efficiently encoding the underlying structure that generates these nuances. However, accurately capturing these effects presents challenges; direct modeling might be computationally expensive. The proposed method uses a pre-processing step involving diffusive operators to mitigate the computational cost while effectively capturing higher-order information. This approach cleverly transforms the high-order effects into a more compressible representation without significantly affecting the underlying data’s integrity, ultimately leading to better compression ratios and accuracy.
Future Extensions#
Future extensions of this research could explore several promising avenues. Extending the methodology to higher-dimensional data is crucial for broader applicability, particularly in scientific domains generating multi-dimensional datasets. Investigating adaptive mechanisms for dynamically adjusting model parameters during compression and decompression would enhance efficiency and robustness for data with varying characteristics. Exploring alternative numerical methods for solving the inverse problem, such as iterative techniques or machine learning-based approaches, might improve computational efficiency. A further investigation into optimal trade-offs between compression ratios, computational costs, and precision control is essential for practical implementation. Finally, integrating domain-specific knowledge into the mechanism learning process, especially through the use of physics-informed models, promises even higher compression rates and better preservation of scientific insight.
More visual insights#
More on figures
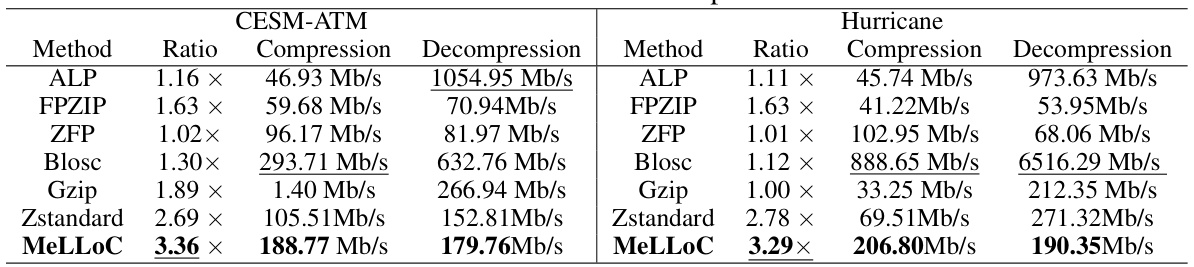
🔼 This figure illustrates the local representation of the difference operator used in the MeLLoC framework. (a) shows the coefficient template, a 9-point stencil that captures the spatial relationships between data points. (b) shows how this local representation translates to intra-predictions within the grid. (c) provides examples of coefficient templates for different types of partial differential equations (PDEs) such as elliptic, hyperbolic, and parabolic.
read the caption
Figure 2: Local representation notations.

🔼 This figure illustrates the concept of precision control in the MeLLoC framework. It shows how the precision of the data (u) and the source term (f) are related. (a) shows the relationship between the number of significant digits in the data and the total number of decimal places, highlighting that the source term (f) has a lower precision than the original data (u), which is crucial for compression. (b) illustrates three scenarios that demonstrate the trade-off between the number of significant digits and the magnitude of the values in the source term. Case I shows a scenario with high precision digits, resulting in a larger magnitude for the source term. Case II shows a scenario where the source term has a large absolute value despite having fewer significant digits. Case III represents the optimal scenario, where a balance is achieved between the magnitude and the number of significant digits in the source term.
read the caption
Figure 3: Illustration of precision control.

🔼 This figure illustrates the periodic continuation used in the Fast Fourier-based Solver method. The data points are extended periodically beyond the original boundaries to create a larger grid. This allows for the application of the efficient Fast Fourier Transform (FFT) for solving the system of equations (1), which significantly accelerates the computation during both compression and decompression. The blue dots represent the original data, and the green and orange dots represent the periodically extended data.
read the caption
Figure 4: Schematic representation of periodic continuation.
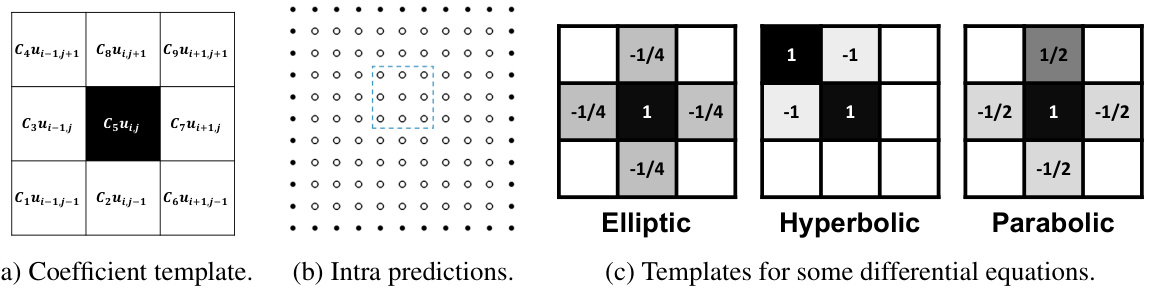
🔼 This figure demonstrates the effectiveness of the proposed compression method on two real-world datasets: CESM-ATM and Hurricane. It shows visualizations of the original data and the corresponding source term after applying the compression technique. The visualizations reveal a significant reduction in the range of values and complexity in the source term compared to the original data, indicating a successful compression process. The small range of values and simpler structure in the source term imply that it is much more compressible than the original data, which is consistent with the main idea of the paper. The low reconstruction errors (10⁻¹¹ for CESM-ATM and 10⁻¹² for Hurricane) further validate the accuracy of the method, demonstrating that it preserves the necessary numerical precision for scientific computations.
read the caption
Figure 5: Demo of the proposed scheme on CESM-ATM and Hurricane datasets.

🔼 This figure displays the frequency distribution of the data before and after applying the compression method. The left two histograms show the distribution of the original CESM-ATM and Hurricane datasets. The right two histograms show the distribution of the corresponding source terms after compression. The use of logarithmic scales highlights the effect of the compression on reducing the range and variability of the data values, leading to a better compression rate.
read the caption
Figure 6: Frequency distribution plots of data before and after compression.
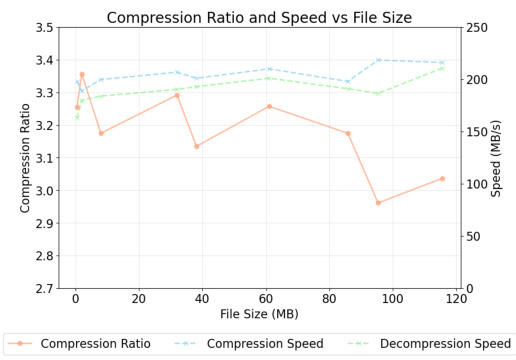
🔼 This figure shows the scalability performance of the MeLLoC compression method across varying file sizes. The orange line represents the compression ratio, which shows a slight decrease as the file size increases, indicating consistent performance even with larger datasets. The blue and green dashed lines represent the compression and decompression speeds, respectively, both remaining relatively stable across the tested file sizes. Compression speed consistently outperforms decompression speed, maintaining an efficient compression process.
read the caption
Figure 7: Performance Metrics Across File Sizes.
Full paper#