Reinforcement Learning with Euclidean Data Augmentation for State-Based Continuous Control

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it tackles the challenge of improving data efficiency in reinforcement learning for continuous control tasks. It introduces a novel data augmentation method that significantly improves the performance of reinforcement learning algorithms, which is a crucial aspect of making these algorithms more practical for real-world applications. This work opens up new avenues for research in data augmentation techniques and efficient reinforcement learning, particularly in robotics and other control systems that operate in a Euclidean space.

Visual Insights

#

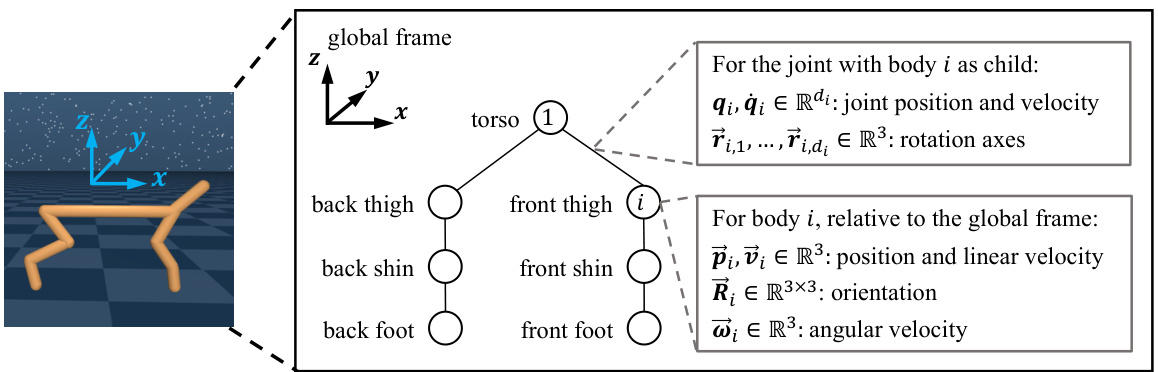
🔼 This figure shows the 2D Cheetah robot from the DeepMind Control Suite. The left panel shows a rendered image of the robot. The right panel provides a schematic representation of the robot’s morphology as a tree graph. Each node in the tree represents a rigid body (limb), and each edge represents a joint connecting two limbs. The figure also illustrates the kinematic features used to represent the robot’s state, including joint positions and velocities, limb positions and velocities, and limb orientations. These features are crucial to the proposed Euclidean data augmentation method in the paper, as they are based on the physical quantities that are directly observable by the agent and are amenable to Euclidean transformations such as rotations.

read the caption

Figure 1: Illustration of Cheetah from DMControl, including its rendering, tree-structured morphology with the nodes being the limbs and the edges the joints, and the state features.

🔼 This table lists kinematic parameters for ten continuous control tasks from the DeepMind Control Suite. For each task, it provides the number of limbs (n), the number of degrees of freedom (DoFs) in the torso (d1), and the counts of joints with 1, 2, and 3 DoFs (n1-DoF, n2-DoF, n3-DoF, respectively). This information is crucial for understanding the complexity of each task and how it relates to the proposed data augmentation method.

read the caption

Table 1: Kinematic parameters of the tasks. n: number of limbs. d1: number of DoFs of the torso limb (i = 1). N1-DoF, N2-DoF, N3-DOF: number of 1-, 2-, 3-DoF joints.

In-depth insights

#

Euclidean Augmentation

#

The concept of “Euclidean Augmentation” in the context of reinforcement learning centers on leveraging the inherent symmetries of Euclidean space (rotations and translations) to generate augmented training data. This approach contrasts with perturbation-based methods, which often introduce less meaningful variations. By applying transformations that preserve Euclidean symmetries, the augmented data retains the underlying dynamics and reward structure of the original data, making it more useful for improving the efficiency and generalization of reinforcement learning models. This is particularly effective for tasks where an agent observes raw physical quantities (e.g., positions and velocities) as state features, as opposed to image-based observations where perturbation-based augmentations have proven successful. However, a critical component is the choice of state representation. Using joint configurations, as commonly done in existing benchmarks, may not be ideal because these are often invariant to Euclidean transformations. Instead, representing states using limb configurations or other physical quantities directly amenable to rotations and translations is crucial for the effectiveness of this data augmentation strategy. This ensures that the transformations yield meaningful augmentations, not just arbitrary noise. The success of Euclidean augmentation thus hinges on selecting appropriate state features and applying symmetry-preserving transformations to create richer and more informative training examples.

Limb-based States

#

The concept of “Limb-based States” in the context of reinforcement learning for robotics introduces a paradigm shift from traditional joint-based state representations. Instead of focusing solely on joint angles and velocities, which are often invariant under Euclidean transformations, a limb-based approach utilizes the position, velocity, and orientation of each rigid body (limb) in the robot’s structure. This offers several key advantages. First, it provides richer state information reflecting the overall configuration of the robot in 3D space, enhancing the agent’s ability to learn complex movements. Second, limb-based states are more amenable to Euclidean data augmentation. This augmentation strategy involves transforming the state features using rotations and translations, generating synthetic data with valid dynamics that increase sample efficiency and potentially lead to improved asymptotic performance. The choice of limb-based representations directly addresses limitations of prior methods, which often showed limited success because the perturbed joint-based states are uncorrelated with the original ones. In essence, limb-based states unlock the potential of symmetry-based data augmentation by providing equivariant features for learning more robust and generalizable policies in continuous control tasks. This methodology is especially beneficial for complex, high-dimensional tasks, where richer state representations provide the necessary information for the agent to learn optimal and generalizable behavior.

DDPG Improvements

#

The paper focuses on enhancing the Deep Deterministic Policy Gradient (DDPG) algorithm for continuous control tasks in reinforcement learning. A core contribution is the introduction of Euclidean data augmentation, leveraging the inherent symmetries in many control problems. Unlike prior perturbation-based methods that often hinder performance, this approach uses transformations like rotations on limb configurations, not just joint angles, to generate augmented data, significantly improving data efficiency. This improvement is especially noticeable on complex tasks with high degrees of freedom. The results show that using limb-based state representation alone provides a boost in performance, further enhanced by the novel data augmentation strategy. The method’s efficacy is demonstrated across various continuous control tasks from the DeepMind Control Suite, showing substantial improvements over standard DDPG and other augmentation techniques like adding Gaussian noise or scaling features. However, the optimal augmentation rate needs task-specific tuning; a key limitation is this lack of task-agnostic hyperparameter selection. The key insight is that exploiting the natural symmetries of the problem, particularly by using a limb-based representation which makes the augmentation meaningful and impactful, yields superior performance compared to unprincipled perturbation methods.

Data Efficiency Boost

#

A significant focus in reinforcement learning (RL) research is enhancing data efficiency. The concept of a ‘Data Efficiency Boost’ implies methods that allow RL agents to learn effectively with less training data. This is crucial because collecting large datasets for RL can be expensive and time-consuming, especially in robotics and continuous control scenarios. Strategies to achieve such a boost often involve data augmentation techniques. These techniques artificially expand the training dataset by generating modified versions of existing data points, improving generalization and potentially reducing overfitting. However, the effectiveness of data augmentation is highly task-dependent, and simply adding noise or random perturbations to the state may not always result in substantial improvements. This paper explores a principled approach to data augmentation using Euclidean symmetries, which are transformations (such as rotations) that preserve the underlying dynamics of the task. By cleverly choosing the state representation and applying suitable transformations, significant improvements in data efficiency are demonstrated. This highlights the importance of carefully designing data augmentation strategies, tailored to the specific structure and symmetries of the task, to optimize learning efficiency in RL.

Future of Symmetries

#

The “Future of Symmetries” in reinforcement learning (RL) holds immense potential. Euclidean symmetries, as explored in the paper, offer a powerful augmentation technique, particularly for state-based continuous control. However, current benchmarks often utilize joint configurations, limiting the applicability of Euclidean transformations. Moving towards limb-based state representations unlocks richer data augmentation possibilities, significantly improving both data efficiency and asymptotic performance. Future research should focus on discovering and exploiting symmetries beyond the Euclidean, including those that might be approximate or task-specific. Automated symmetry discovery methods, which could analyze the dynamics of the environment and automatically generate suitable transformations, would be particularly impactful. This would move beyond manual identification of symmetries and create more adaptable augmentation strategies. Combining symmetry-based augmentation with other techniques, such as contrastive learning, might lead to even more robust and efficient RL algorithms. Finally, exploring the use of equivariant neural networks in conjunction with improved augmentation methods could further enhance performance and understanding of the role of symmetries in RL.

More visual insights

#

More on figures

🔼 This figure illustrates the SOĝ(3) rotation applied to the Cheetah robot during data augmentation. The top panel shows the original pose of the robot in the global coordinate frame (x, y, z). The gravity vector ğ points downwards along the negative z-axis. The robot’s displacement vector 𝑑 points to the right. The bottom panel shows the same robot after a rotation Rα about the z-axis (yaw), transforming the displacement vector to 𝑑′. Note that the gravity vector remains unchanged due to the restriction that the rotations are limited to those around the z-axis (yaw-only rotations). This rotation Rα ∈ SOĝ(3) is used for data augmentation in the paper.

read the caption

Figure 2: SOĝ(3) rotation in Cheetah.

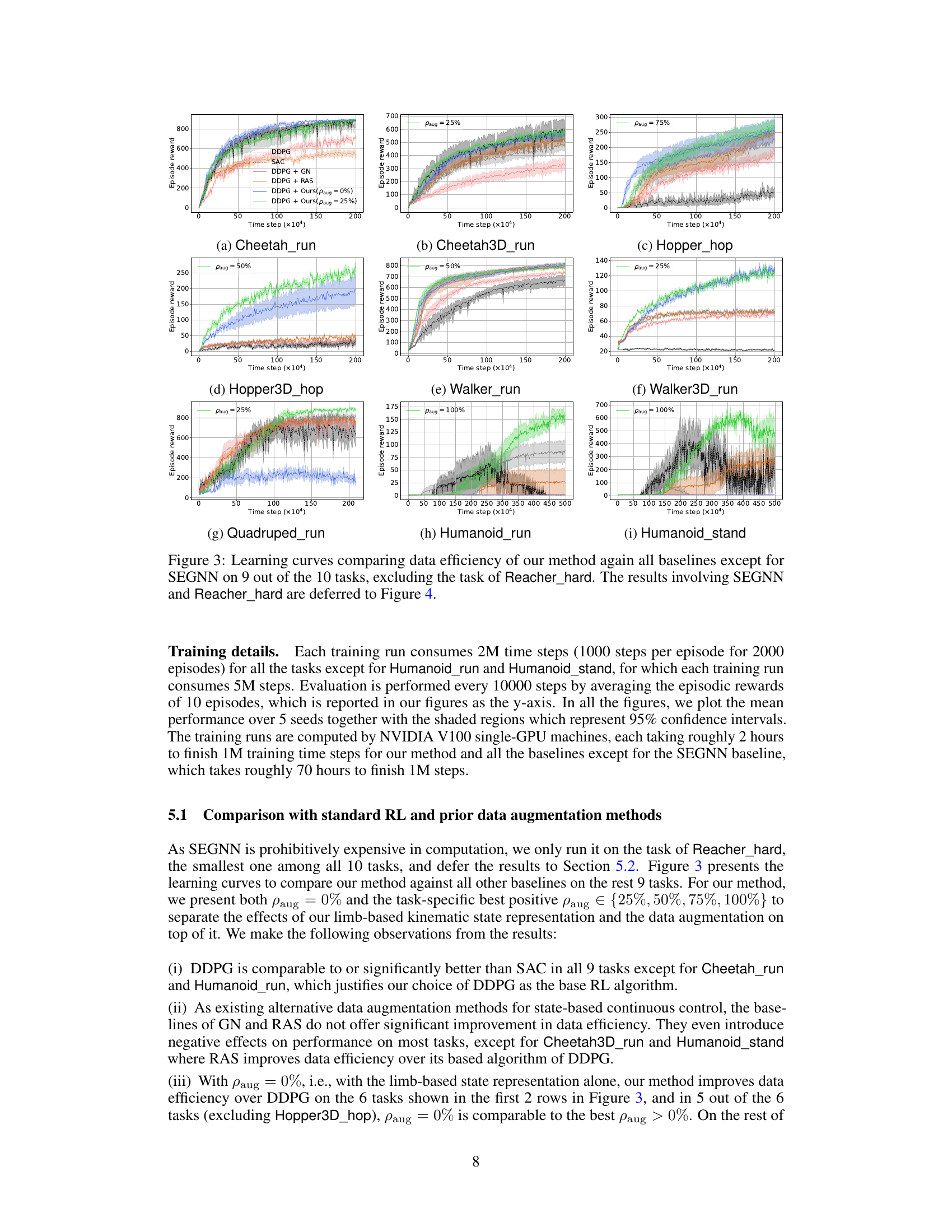
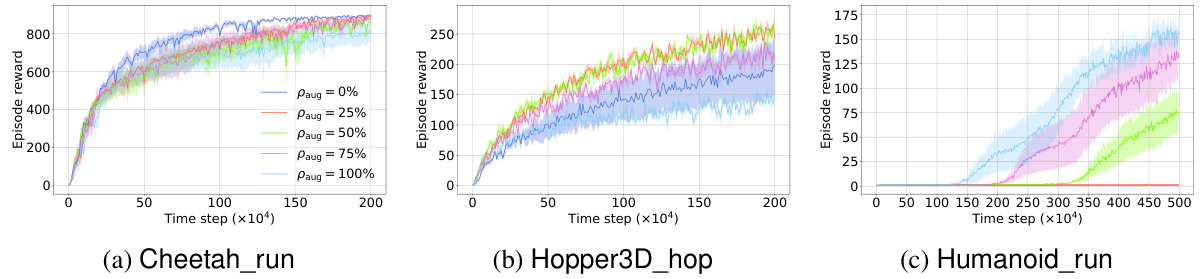
🔼 This figure presents learning curves for nine out of ten continuous control tasks from the DeepMind Control Suite. The curves compare the performance of the proposed Euclidean data augmentation method against several baselines, including standard DDPG, SAC, DDPG with Gaussian noise, DDPG with random amplitude scaling, and the proposed method without data augmentation (paug=0%). For the proposed method, results are shown for the best performing paug values (percentage of augmentations performed in each batch of training data) and paug=0%. The figure demonstrates that the proposed method generally outperforms baselines in terms of data efficiency, especially on the more challenging tasks.

read the caption

Figure 3: Learning curves comparing data efficiency of our method again all baselines except for SEGNN on 9 out of the 10 tasks, excluding the task of Reacher_hard. The results involving SEGNN and Reacher_hard are deferred to Figure 4.

🔼 This figure compares the learning curves of different methods for nine out of ten continuous control tasks. It shows the episode reward over time for several approaches: standard DDPG, SAC (Soft Actor-Critic), DDPG with Gaussian noise (GN), DDPG with random amplitude scaling (RAS), DDPG with the proposed Euclidean data augmentation method (Ours) with different augmentation ratios (0% and 25%), and DDPG with SEGNN (equivariant neural network). The figure illustrates the improved data efficiency of the proposed method compared to baselines and highlights the impact of limb-based kinematic representation and Euclidean data augmentation on different task complexities. The Reacher_hard task’s results are shown separately in a later figure.

read the caption

Figure 3: Learning curves comparing data efficiency of our method again all baselines except for SEGNN on 9 out of the 10 tasks, excluding the task of Reacher_hard. The results involving SEGNN and Reacher_hard are deferred to Figure 4.

🔼 This figure compares the learning curves of different methods for solving 9 continuous control tasks from the DeepMind Control Suite. The methods compared include standard DDPG and SAC baselines, DDPG with Gaussian noise and random amplitude scaling data augmentation, and the proposed method with limb-based kinematic features and Euclidean data augmentation. The x-axis represents training time steps, and the y-axis represents the average episodic reward. The shaded regions indicate 95% confidence intervals. The results for Reacher_hard task and comparison with SEGNN are presented separately in Figure 4.

read the caption

Figure 3: Learning curves comparing data efficiency of our method again all baselines except for SEGNN on 9 out of the 10 tasks, excluding the task of Reacher_hard. The results involving SEGNN and Reacher_hard are deferred to Figure 4.

🔼 This figure compares the learning curves of different methods on 9 out of 10 tasks (excluding Reacher_hard). It shows the episode reward over time for several methods, including the proposed method with different augmentation rates (paug), standard DDPG, SAC, DDPG with Gaussian noise (GN), and DDPG with random amplitude scaling (RAS). The graph helps visualize the data efficiency and asymptotic performance of each approach. Results for the Reacher_hard task and the SEGNN (equivariant neural network) baseline are presented separately in another figure.

read the caption

Figure 3: Learning curves comparing data efficiency of our method again all baselines except for SEGNN on 9 out of the 10 tasks, excluding the task of Reacher_hard. The results involving SEGNN and Reacher_hard are deferred to Figure 4.

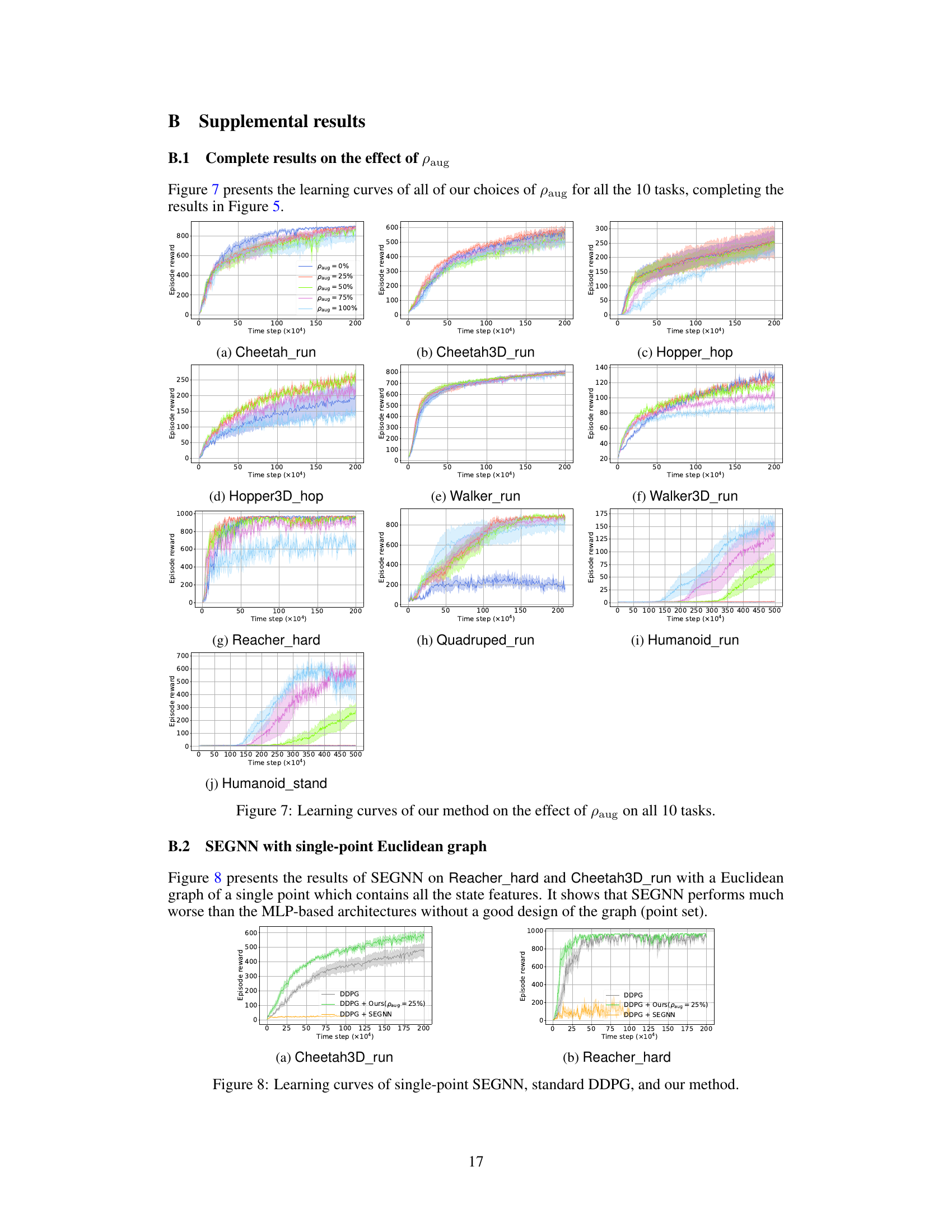
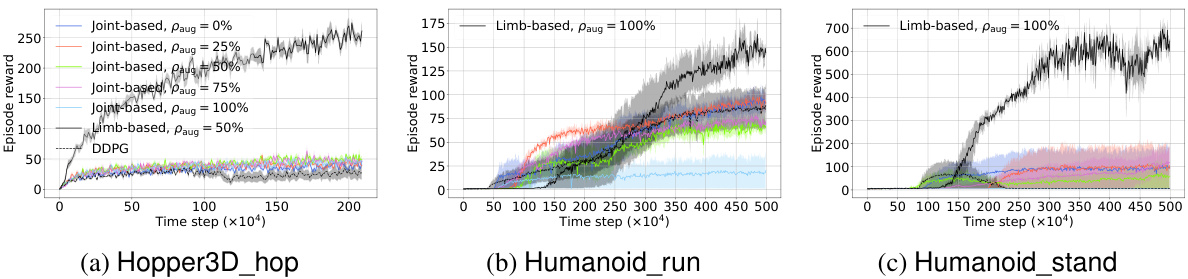
🔼 This figure displays the learning curves for the proposed method across different values of paug (proportion of data augmentation) on ten continuous control tasks. Each subplot represents a task, showing the average episodic reward over time. The various colors represent different values of paug , illustrating how the degree of data augmentation impacts learning performance on each task. The results demonstrate the effectiveness of data augmentation on some tasks while showing a more complex relationship between performance and paug on others. This helps to understand the generalizability and optimal usage of the data augmentation.

read the caption

Figure 7: Learning curves of our method on the effect of paug on all 10 tasks.

🔼 This figure compares the learning curves of different methods for 9 out of 10 continuous control tasks. The y-axis represents the episodic reward, and the x-axis shows the timestep. The methods compared include standard DDPG, SAC, DDPG with Gaussian noise augmentation, DDPG with random amplitude scaling augmentation, and the proposed method (DDPG with Euclidean data augmentation) with different augmentation rates (paug). The figure highlights the improved data efficiency of the proposed method, especially compared to the perturbation-based augmentation methods.

read the caption

Figure 3: Learning curves comparing data efficiency of our method again all baselines except for SEGNN on 9 out of the 10 tasks, excluding the task of Reacher_hard. The results involving SEGNN and Reacher_hard are deferred to Figure 4.

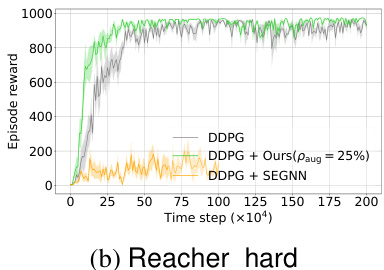
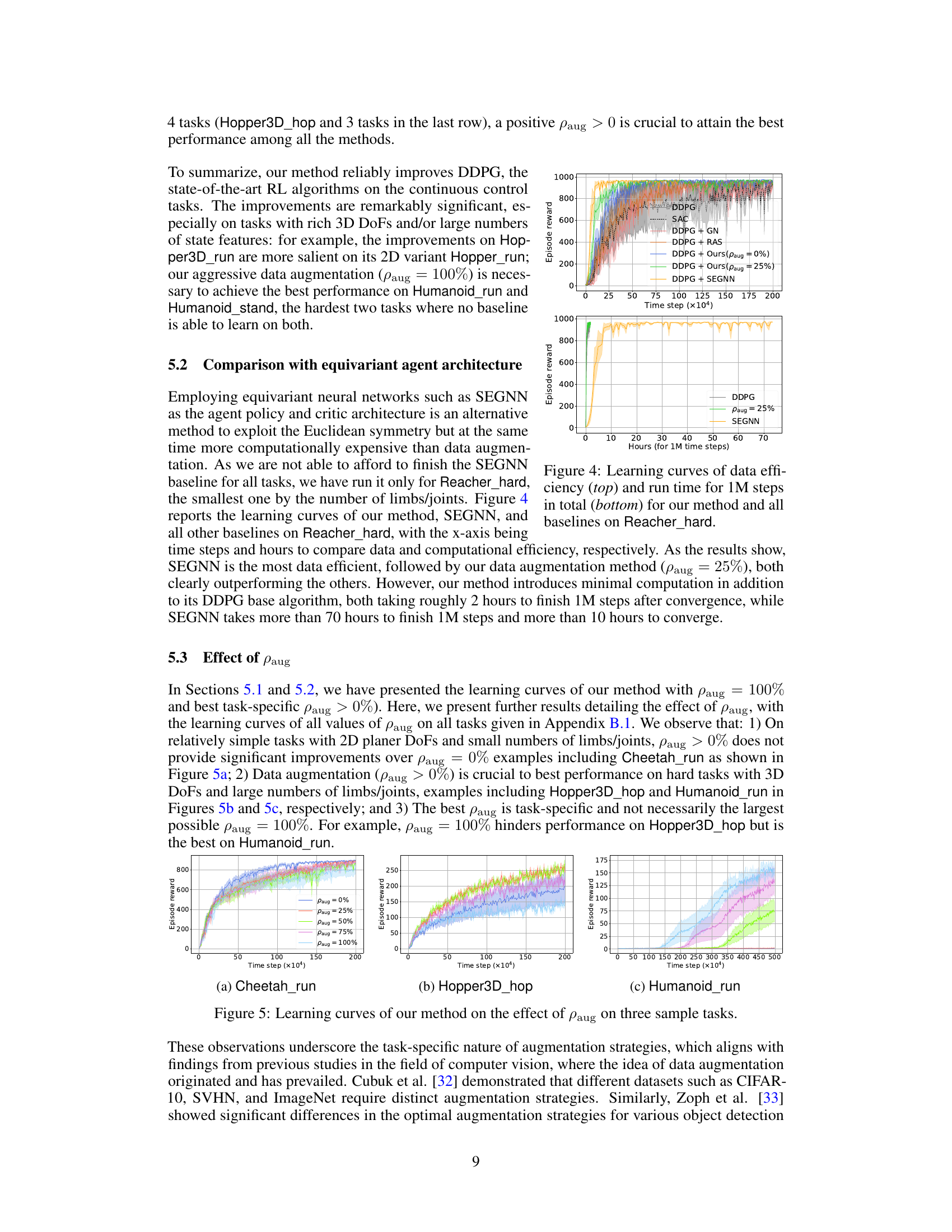
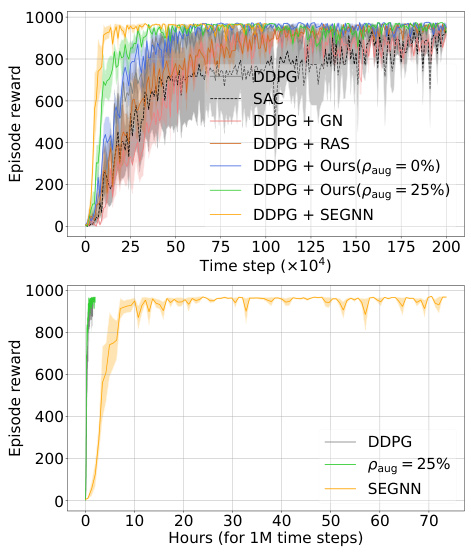
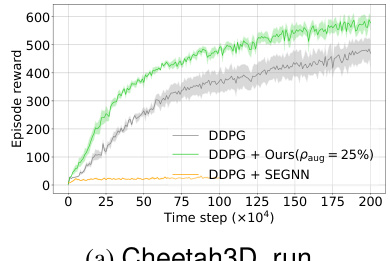
🔼 This figure compares the performance of different methods on the Reacher_hard task. The top part shows the learning curves, illustrating how quickly each method learns to achieve a high reward. The bottom part shows the computational cost (run time) for each method to process 1 million time steps. It demonstrates the trade-off between data efficiency and computational cost, highlighting the efficiency of the proposed method.

read the caption

Figure 4: Learning curves of data efficiency (top) and run time for 1M steps in total (bottom) for our method and all baselines on Reacher_hard.

More on tables

🔼 This table lists the sensory observations for all ten tasks in the paper. It categorizes them into invariant and equivariant features under SOĝ(3) rotations. Invariant features remain unchanged under these rotations, while equivariant features transform according to the rotation. The table provides a count of each type of feature for each task, offering a detailed view of the sensory input used in the experiments.

read the caption

Table 2: Sensory observations in the tasks.

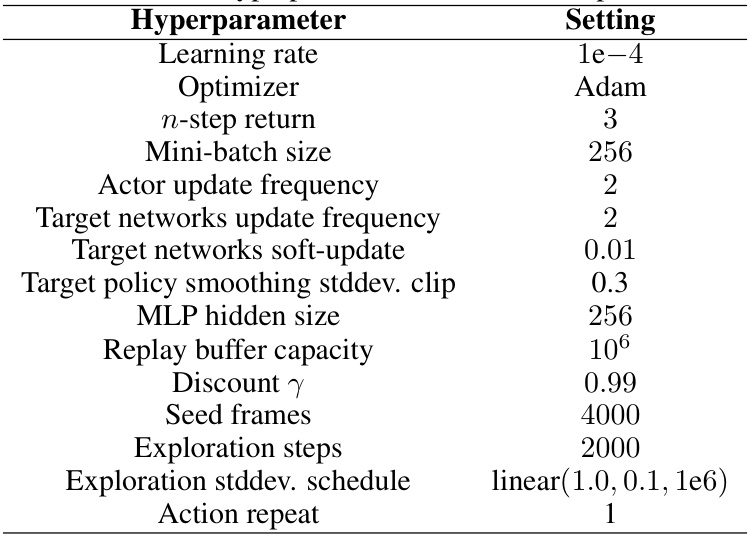
🔼 This table lists the hyperparameters used for the Deep Deterministic Policy Gradient (DDPG) algorithm in the experiments. It details settings for learning rate, optimizer, n-step return, mini-batch size, actor and target network update frequencies, target network soft-update, target policy smoothing, MLP hidden size, replay buffer capacity, discount factor, seed frames, exploration steps, exploration standard deviation schedule, and action repeat.

read the caption

Table 3: DDPG hyperparameters used in our experiments.

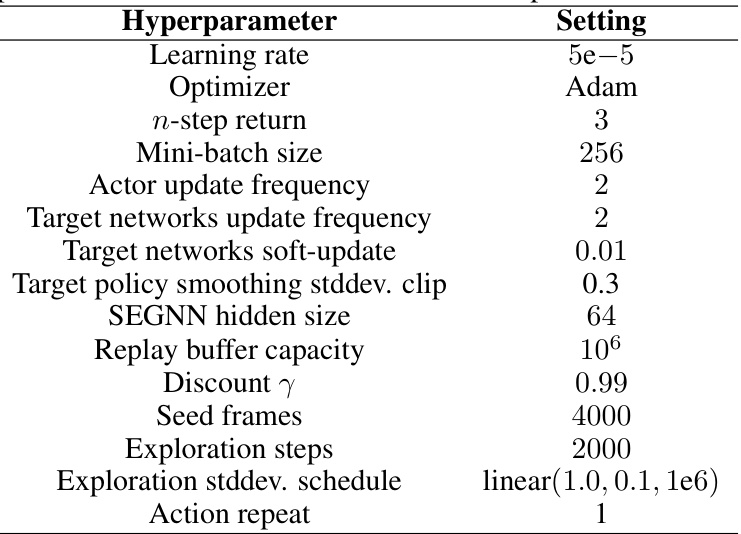
🔼 This table lists the hyperparameters used in the SEGNN-based DDPG implementation for the Reacher_hard task. It includes settings for the learning rate, optimizer, n-step return, mini-batch size, actor and target network update frequencies, target network soft update, target policy smoothing standard deviation clip value, SEGNN hidden size, replay buffer capacity, discount factor, seed frames, exploration steps, exploration standard deviation schedule, and action repeat.

read the caption

Table 4: Hyperparameters for our SEGNN-based DDPG implementation for Reacher_hard.

Full paper

#