SEEV: Synthesis with Efficient Exact Verification for ReLU Neural Barrier Functions

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because safe and reliable autonomous systems are paramount. The research directly addresses a critical challenge in ensuring safety by improving the efficiency and reliability of Neural Control Barrier Function (NCBF) verification. This opens avenues for broader adoption of NCBFs in safety-critical applications and inspires further research in efficient verification techniques for complex neural network-based systems.

Visual Insights

#

This figure illustrates the SEEV framework, which consists of two main components: a synthesis component and a verification component. The synthesis component trains a ReLU Neural Control Barrier Function (NCBF) using a novel regularizer to reduce the number of activation regions at the safety boundary. The verification component efficiently verifies the safety of the synthesized NCBF by exploiting tight over-approximations of the safety conditions. The figure shows a feedback loop between the two components: counterexamples found during verification are used to refine the training dataset, improving the quality and efficiency of the overall process.

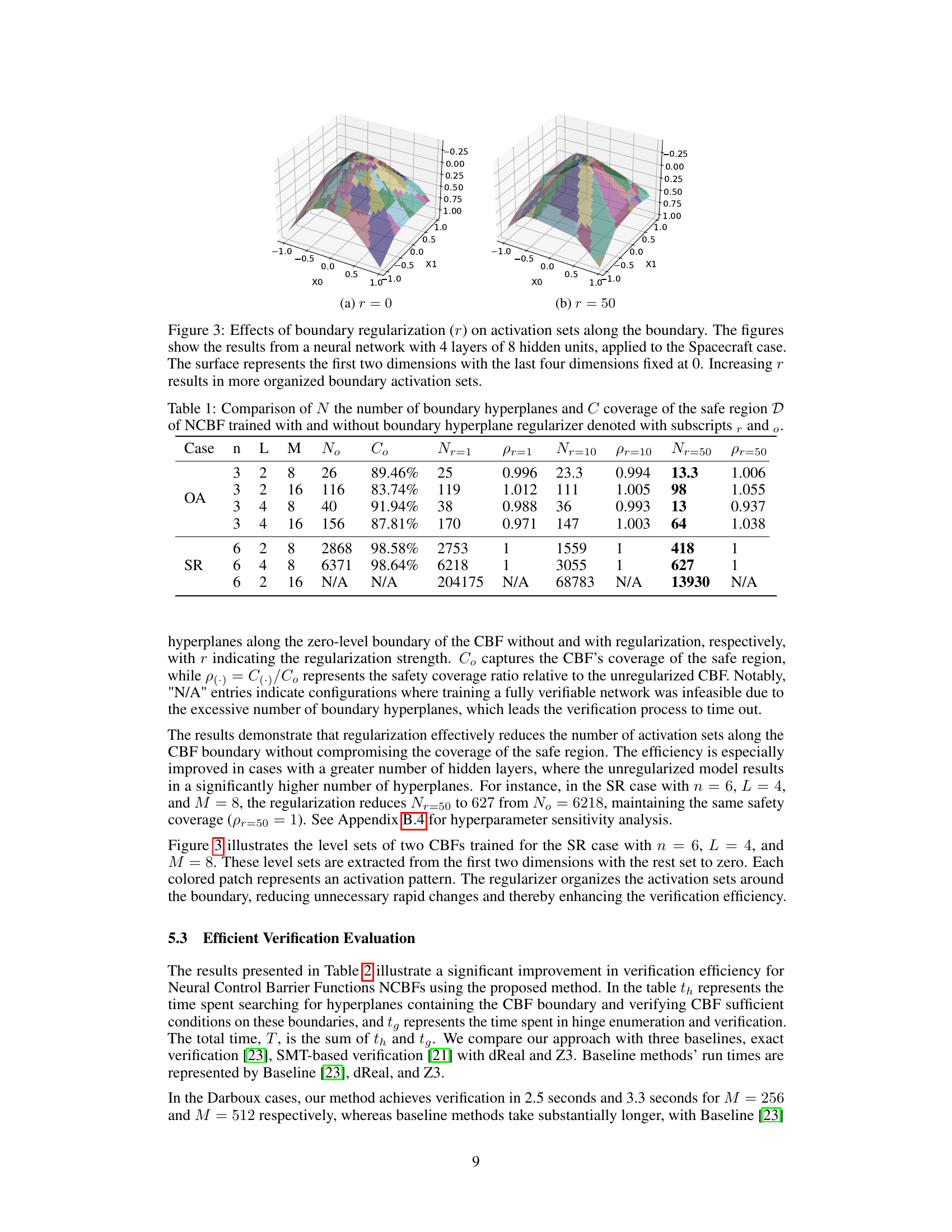
This table compares the number of boundary hyperplanes (N) and the coverage of the safe region (C) for neural control barrier functions (NCBFs) trained with and without a boundary hyperplane regularizer. The regularizer strength is varied (r=1, r=10, r=50), showing its effect on reducing the number of hyperplanes while maintaining safety coverage. The results are shown for different network architectures and system examples (OA and SR).

In-depth insights

#

NCBF Synthesis

#

NCBF synthesis tackles the challenge of creating neural control barrier functions (NCBFs) that effectively enforce safety constraints in control systems. The core problem is to learn a neural network that acts as a barrier function, ensuring the system’s state remains within a safe region. This involves careful consideration of the neural network’s architecture, activation functions (often ReLU for its piecewise linearity), and training methods. Effective synthesis techniques must balance expressiveness—the ability to represent complex safety constraints—with verifiability—the assurance that the learned NCBF guarantees safety. This is a crucial aspect because a flawed NCBF could lead to unsafe behavior. A common approach involves incorporating safety verification directly into the training process, using counterexamples to iteratively refine the NCBF. Regularization techniques might be applied to constrain the network’s complexity and thus enhance verification efficiency. Overall, NCBF synthesis strives for efficient and reliable algorithms that produce safe and effective controllers, a highly active area of research due to its importance in robotics and autonomous systems.

Efficient Verification

#

Efficient verification of neural network-based safety controllers is crucial for deploying autonomous systems. The core challenge lies in the computational complexity of analyzing all possible activation regions of the neural network, especially near safety boundaries. Existing methods often struggle with scalability, especially for high-dimensional systems or deep networks. This paper addresses this limitation by proposing innovative techniques to significantly improve verification efficiency. The introduction of novel regularizers during the training phase reduces the number of activation regions, thereby minimizing the verification workload. Furthermore, tight over-approximations of safety conditions are leveraged to expedite verification, resulting in substantial speedups. This combination of clever synthesis and verification algorithms represents a significant contribution, enabling faster and more reliable safety verification in practical applications.

Regularization Impact

#

The impact of regularization on the performance of neural control barrier functions (NCBFs) is a crucial aspect of the SEEV framework. Regularization helps reduce the number of activation regions near the safety boundary, which directly translates to a significant decrease in computational complexity during verification. This is achieved by encouraging similar activation patterns along the boundary, thus simplifying the piecewise-linear structure. The effectiveness of the regularization is evident in the simulation results, where the reduced number of activation regions leads to substantially faster verification times without compromising safety. However, careful selection of the regularization hyperparameters is crucial to balance the reduction in complexity against the potential loss of accuracy or safety coverage. The choice of regularization strength involves a trade-off between computational efficiency and the quality of the resulting CBF. Further investigation could explore adaptive or data-driven methods for dynamically adjusting the regularization strength during training to optimize this trade-off.

CEGIS Framework

#

A CEGIS (Counterexample-Guided Inductive Synthesis) framework for neural network synthesis would iteratively refine a neural network model. The process starts with an initial network, which is then verified against safety specifications. If the verification fails, a counterexample demonstrating the network’s inadequacy is generated. This counterexample is used to improve the network through training or architectural adjustments, after which the verification process repeats. The iterative refinement continues until a network satisfying the specifications is obtained or a termination condition is met. Crucially, the efficiency of the CEGIS process depends heavily on the effectiveness of both the verification and the synthesis steps: a strong verifier quickly identifies failures, while an effective synthesizer generates improved models based on counterexamples. The design of the synthesizer is especially critical, as it directly influences the convergence speed and quality of the final model. A well-designed CEGIS framework should also incorporate mechanisms to handle complex safety properties and prevent the synthesis process from getting stuck in local optima. Overall, effective use of CEGIS necessitates careful attention to the trade-off between the verification and synthesis complexity and efficiency.

Future Research

#

Future research directions stemming from this work on efficient neural control barrier function (NCBF) synthesis and verification could explore several promising avenues. Extending the approach to handle more complex neural network architectures beyond ReLU networks, such as those employing more expressive activation functions or recurrent structures, is crucial for broader applicability. Investigating the scalability of the proposed methods to higher-dimensional systems remains a challenge and warrants further research. While the current work focuses on continuous-time systems, adapting the framework for discrete-time systems would be beneficial for practical implementations. Finally, developing more sophisticated techniques for automatically generating tighter over-approximations in verification could significantly reduce computational costs and improve efficiency, particularly for complex system models.

More visual insights

#

More on figures

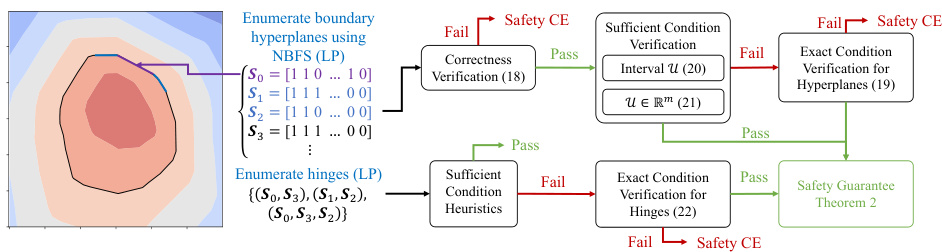
This figure presents a flowchart illustrating the efficient exact verification process for ReLU Neural Control Barrier Functions (NCBFs). It starts by enumerating boundary hyperplanes and hinges using a breadth-first search algorithm. Then, it proceeds hierarchically through verification stages. First, it checks sufficient conditions; if these fail, it moves to computationally more expensive exact verification steps. The process continues until either a safety guarantee is proven or a counterexample is found. Each stage uses efficient algorithms to reduce computational costs.

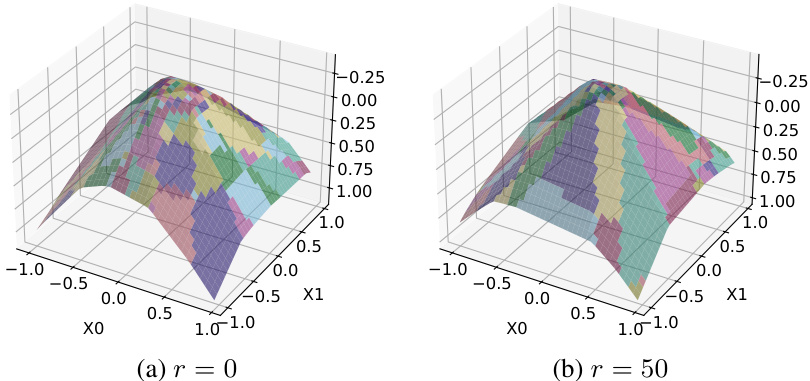
This figure visualizes the impact of the boundary regularization hyperparameter (r) on the organization of activation sets near the decision boundary of a neural network. Two 3D plots show the activation patterns for r=0 and r=50. Increasing r leads to a more structured and less fragmented pattern, indicating improved efficiency in the verification process.

More on tables

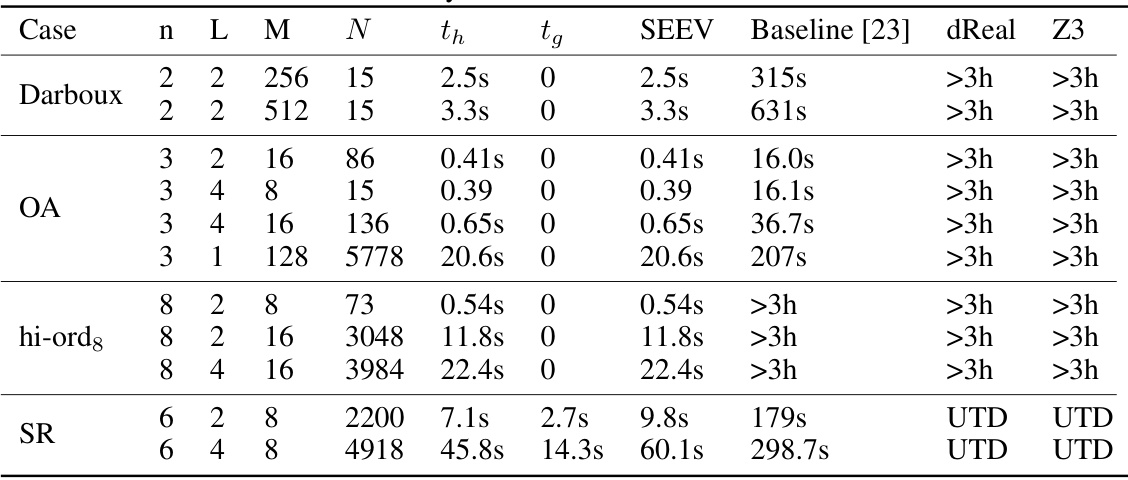
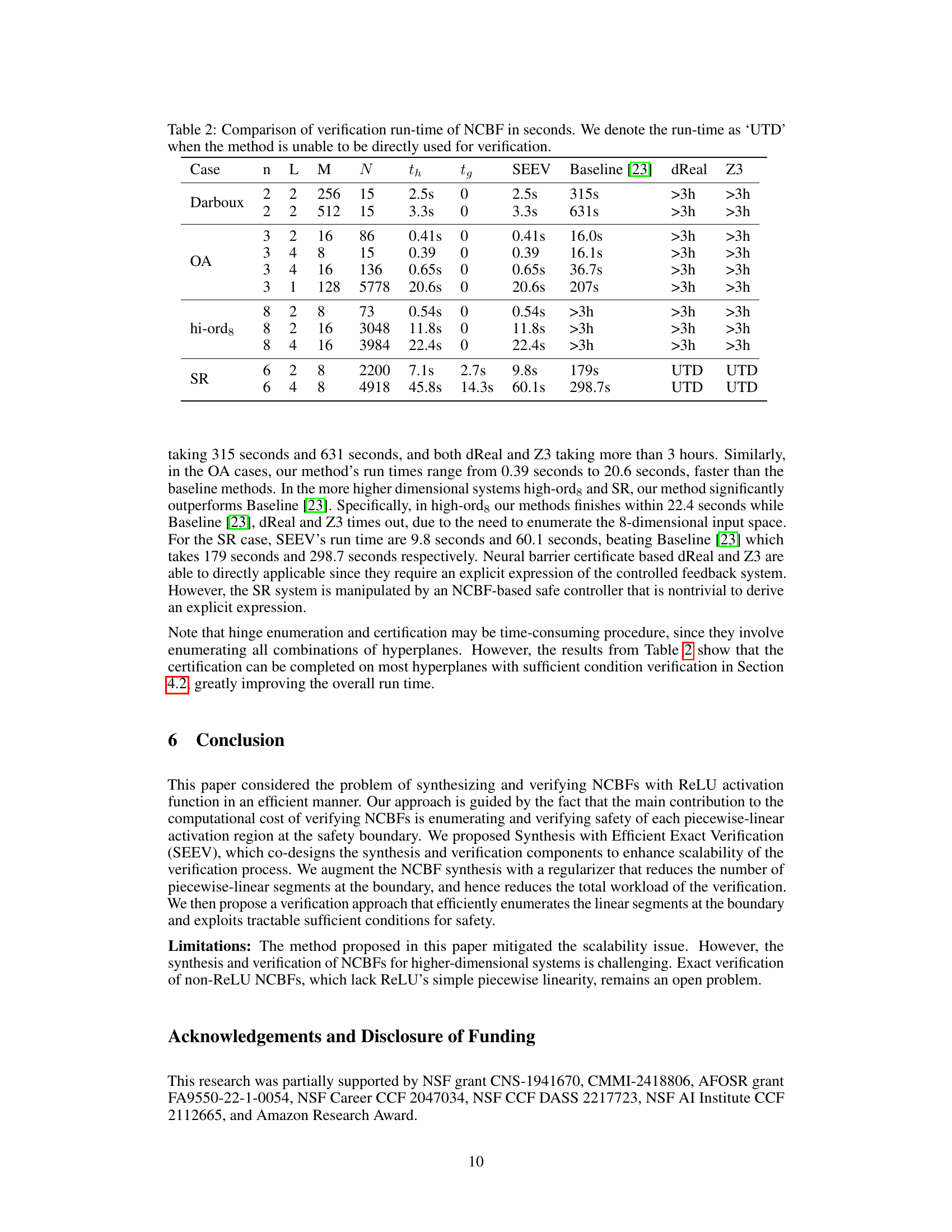
This table compares the verification time of Neural Control Barrier Functions (NCBFs) using four different methods: the proposed SEEV method, the baseline method from a previous study [23], and two other methods using dReal and Z3. The table shows the verification time for different system models (Darboux, OA, hi-ords, SR) with varying neural network architectures (number of layers and hidden units). The ‘UTD’ value means that the method was unable to verify the NCBF within a reasonable time frame. The table illustrates SEEV’s efficiency compared to the baseline and other methods, especially in higher-dimensional systems.

This table compares the verification time (in seconds) of the proposed SEEV method against three baseline methods (Baseline [23], dReal, and Z3) for different system models (Darboux, OA, hi-ord8, and SR) with varying network structures (n, L, M). The run-time is denoted as ‘UTD’ when the baseline method is not directly applicable for verification. The results demonstrate SEEV’s improved efficiency, particularly in higher-dimensional systems where baseline methods time out.

This table compares the verification time of the proposed SEEV method against three baseline methods (exact verification [23], dReal, and Z3) for four different systems (Darboux, Obstacle Avoidance, hi-ord8, and Spacecraft Rendezvous) with varying network sizes. The runtimes are given in seconds, and ‘UTD’ indicates that the method was unable to complete verification within a reasonable timeframe. It demonstrates the significant speedup achieved by SEEV, particularly for higher-dimensional systems.

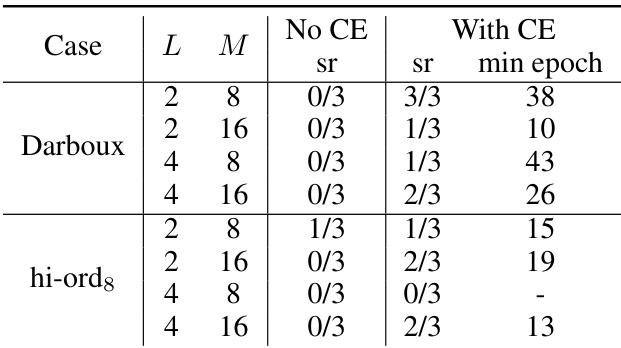
This table presents the success rates and minimum number of epochs needed for successful training and certification of Control Barrier Functions (CBFs) with and without counter-example guided training. It compares the performance for different network structures (layers and hidden units) on the Darboux and hi-ord8 systems.

This table compares the verification run-time of Neural Control Barrier Functions (NCBFs) using four different methods: SEEV (the proposed method), Baseline [23], dReal, and Z3. The table shows the run-time for different systems (Darboux, OA, hi-ord8, SR) with varying network sizes (n, L, M). UTD indicates that the method was unable to perform the verification within a reasonable time frame. The table highlights SEEV’s superior efficiency.

This table compares the verification run-time (in seconds) of the proposed SEEV method against three baselines: exact verification [23], and SMT-based verification using dReal and Z3. The table shows that SEEV significantly outperforms the baselines, especially in higher-dimensional systems (hi-ord8 and SR), where the baselines often time out. The run-times are categorized by system (Darboux, OA, hi-ord8, SR), neural network architecture (specified by n, L, and M), and number of hyperplanes (N). UTD indicates that a method was unable to be used for verification.

Full paper

#