↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning models, especially Graph Neural Networks (GNNs), are susceptible to adversarial attacks, where small input changes significantly alter outputs. While existing research focuses on pre-processing and model adaptation, the impact of weight initialization remains largely unexplored. This is a major problem because poorly initialized models are highly vulnerable, leading to unreliable predictions.
This paper investigates the relationship between weight initialization strategies and a model’s resilience to these attacks. The researchers introduce a theoretical framework linking initial weights and training epochs to robustness. Their experiments across various models and datasets demonstrate that careful weight initialization significantly improves model robustness against several attack types, sometimes by up to 50%, without sacrificing accuracy on clean data. This provides a valuable new perspective on enhancing model security.
Key Takeaways#
Why does it matter?#
This paper is crucial because it reveals a previously unexplored vulnerability in GNNs and DNNs: their sensitivity to weight initialization. This finding challenges existing robustness strategies and opens exciting avenues for improving model security and reliability in various applications.
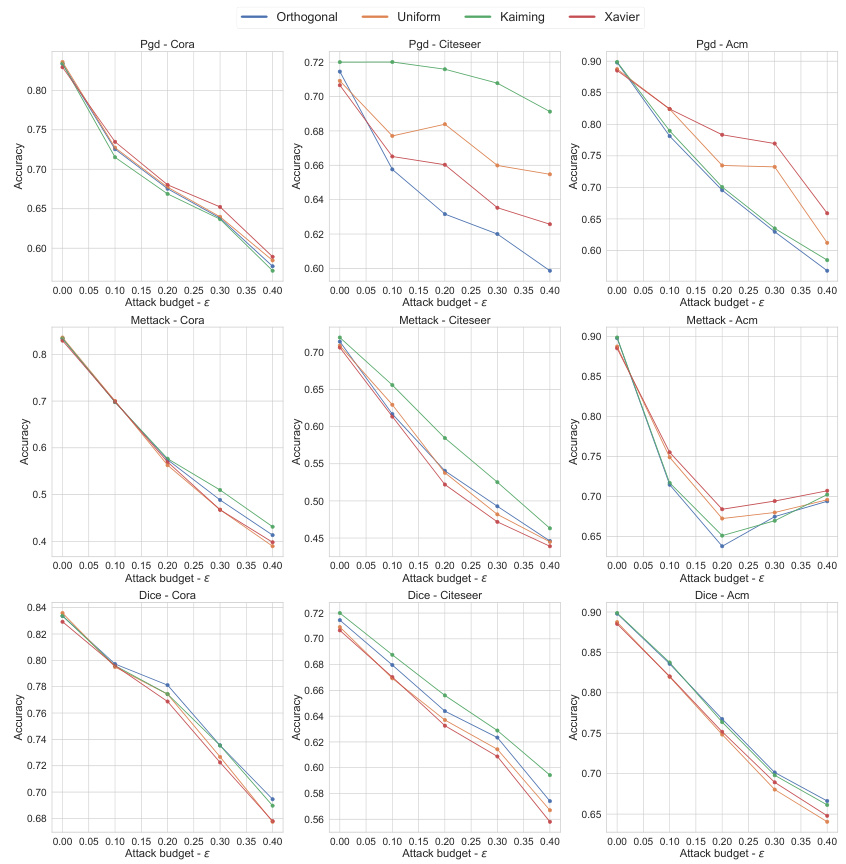
Visual Insights#

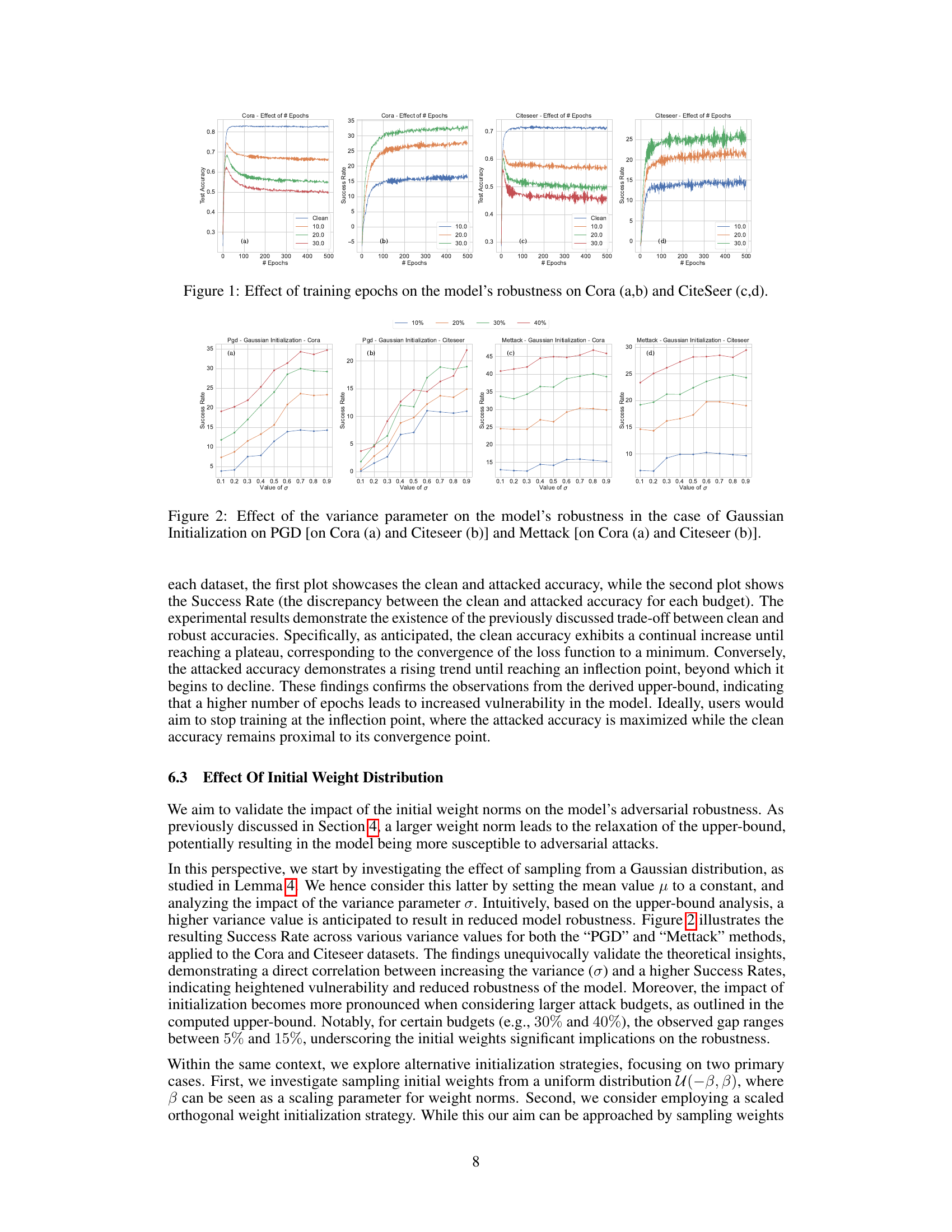
This figure displays the impact of the number of training epochs on a model’s robustness against adversarial attacks. Subplots (a) and (b) show the results for the Cora dataset, while (c) and (d) show the results for the CiteSeer dataset. Each subplot contains two graphs. The top graph shows the test accuracy (clean accuracy and accuracy under attack) as a function of the number of epochs. The bottom graph shows the success rate of adversarial attacks (difference between clean accuracy and attacked accuracy) as a function of the number of epochs. The results demonstrate a trade-off between clean accuracy and robustness: increasing the number of epochs initially improves clean accuracy but eventually leads to reduced robustness against attacks.

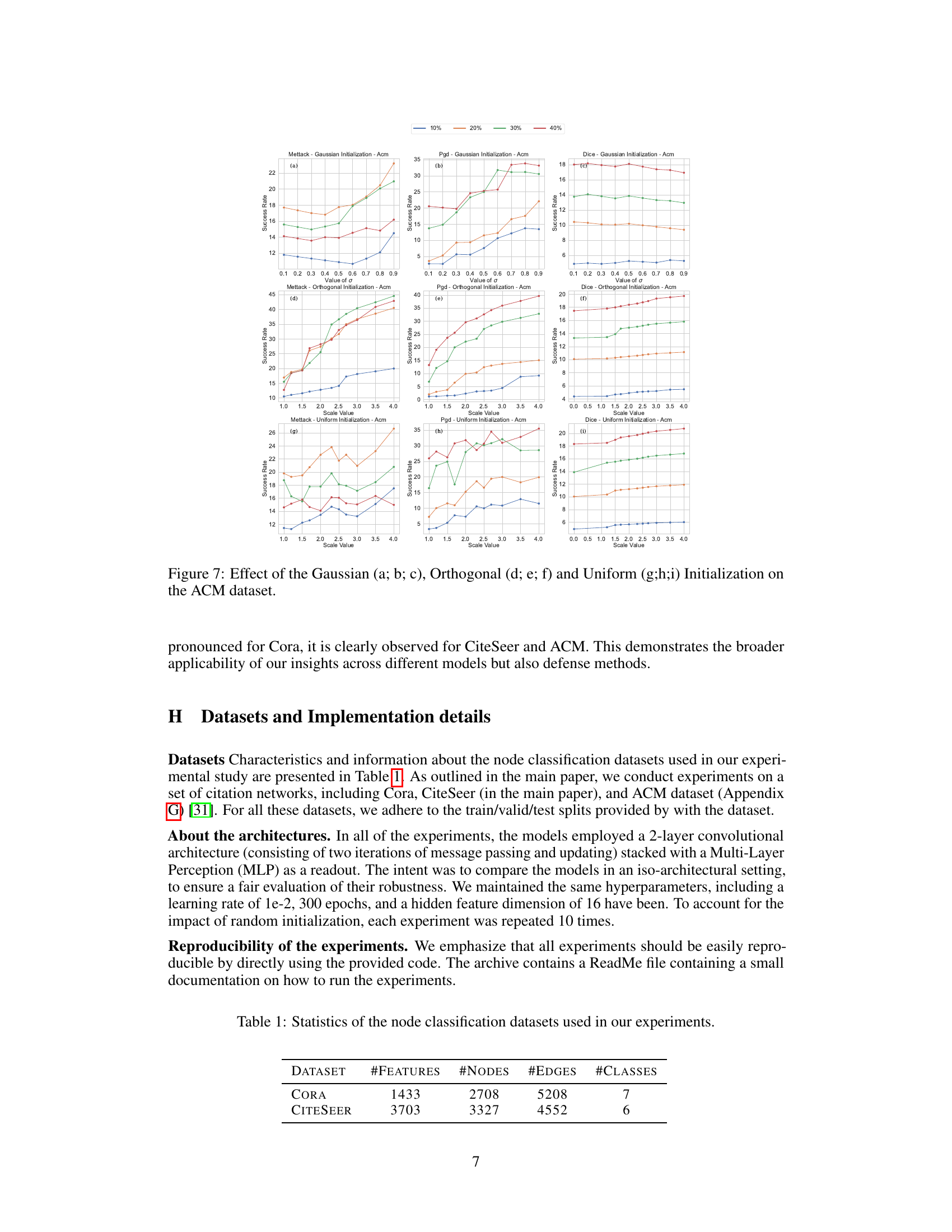
This table presents the characteristics of the Cora and CiteSeer datasets used for node classification experiments in the paper. For each dataset, it lists the number of features per node, the total number of nodes, the number of edges, and the number of classes.
In-depth insights#
Robust GNN Init#
The heading ‘Robust GNN Init’ suggests a focus on improving the robustness of Graph Neural Networks (GNNs) through careful weight initialization. Robustness, in this context, likely refers to the GNN’s resilience against adversarial attacks or noisy data. The paper likely explores different initialization strategies (e.g., Xavier, Kaiming, orthogonal) and analyzes their impact on a GNN’s performance under various attack scenarios. A key aspect would be demonstrating that a specific initialization technique leads to superior performance and enhanced resistance to adversarial examples compared to alternative methods. The research might involve both theoretical analysis (e.g., deriving bounds on adversarial robustness based on initialization) and empirical evaluation (testing different initializations on real-world datasets under various attacks). The ultimate goal is likely to propose a best practice for GNN initialization that promotes both accuracy on clean data and strong robustness against perturbations.
Adversarial Risk#
The concept of ‘Adversarial Risk’ in the context of graph neural networks (GNNs) and deep neural networks (DNNs) centers on quantifying a model’s vulnerability to adversarial attacks. It represents the expected error or deviation in a model’s prediction when subjected to carefully crafted perturbations of the input data (graph structure or node features for GNNs, and input features for DNNs). The key is that these perturbations are designed to be subtle and undetectable by human observers, while maximally impacting the model’s accuracy. Lower adversarial risk signifies a more robust and resilient model. This concept is crucial for understanding and improving model security in safety-critical applications. Measuring adversarial risk typically involves evaluating the model’s performance on a set of adversarially perturbed inputs, comparing it to performance on clean data. The difference highlights the vulnerability or robustness of the model. The paper likely explores methods to quantify and reduce this risk, possibly by analyzing the impact of different training techniques and weight initialization strategies. The framework for analyzing adversarial risk should be mathematically rigorous, providing a solid theoretical foundation for interpreting experimental results and guiding further research in adversarial robustness.
Weight Init Effects#
The study of weight initialization effects on model robustness reveals a crucial, often overlooked aspect of adversarial defense. Appropriate weight initialization strategies, in conjunction with the number of training epochs, significantly impact a model’s resilience against adversarial attacks. The theoretical framework established directly links initial weight norms and the number of training epochs to an upper bound on adversarial risk. This framework is not limited to Graph Neural Networks (GNNs), but rather extends to a broader class of deep neural networks. Empirically, the findings validate the theoretical analysis, showing that smaller initial weight norms correlate with improved robustness. However, a crucial trade-off emerges: while smaller initial weights enhance robustness, they can negatively affect performance on clean data. The optimal strategy involves balancing these competing factors, carefully selecting initial weight distributions and training duration to maximize both clean accuracy and adversarial resilience. This research highlights the importance of considering weight initialization as a critical component of robust model design, and not merely as a factor impacting convergence speed or generalization. The results suggest a path towards more robust models through careful tuning of these often-overlooked hyperparameters.
Epoch Impact#
The analysis of ‘Epoch Impact’ in the research paper reveals a crucial interplay between the number of training epochs and a model’s robustness against adversarial attacks. Increasing the number of epochs, while improving clean accuracy, paradoxically increases vulnerability to adversarial perturbations. This is because extended training allows the model to overfit to the training data, losing its ability to generalize and resist carefully crafted attacks. The theoretical upper bound derived in the paper directly supports this observation, demonstrating a direct relationship between the number of epochs and the looseness of the robustness bound. Experimentally, this trade-off is clearly illustrated, showing an initial rise in attacked accuracy followed by a decline after reaching an inflection point. This finding highlights the importance of carefully selecting the optimal number of training epochs to achieve a balance between clean accuracy and robustness, underscoring the need for strategies that mitigate this inherent trade-off for improved model security and reliability.
DNN Generalization#
The concept of “DNN Generalization” within the context of adversarial robustness focuses on extending the study’s findings beyond Graph Neural Networks (GNNs) to encompass the broader class of Deep Neural Networks (DNNs). The authors argue that the theoretical framework linking weight initialization to adversarial robustness is not specific to GNNs but rather applicable to various DNN architectures. This generalization is a crucial contribution, broadening the impact and relevance of their work. The theoretical upper bound derived for GNNs is extended, demonstrating that similar relationships between initialization, training epochs, and adversarial robustness hold for general DNNs. This highlights a fundamental principle of neural network training rather than a GNN-specific phenomenon. This generalization is supported by experimental results on DNNs, showing the impact of various initialization strategies and the number of training epochs on robustness. However, the experimental validation of the generalization requires further investigation across diverse DNN architectures and datasets to solidify its claim as a universal property of DNNs. This section provides valuable insights into designing robust DNNs through careful consideration of initialization, but more empirical evidence is needed to confirm its broad applicability beyond the scope of the specific DNN architectures considered in the experiments.
More visual insights#
More on figures
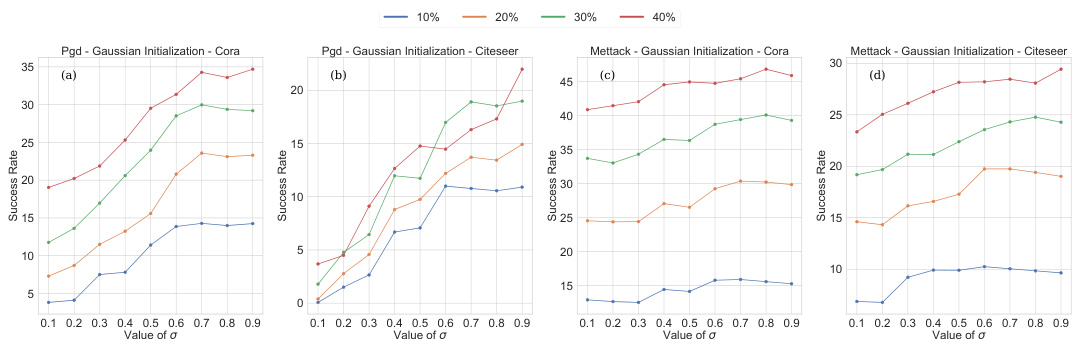
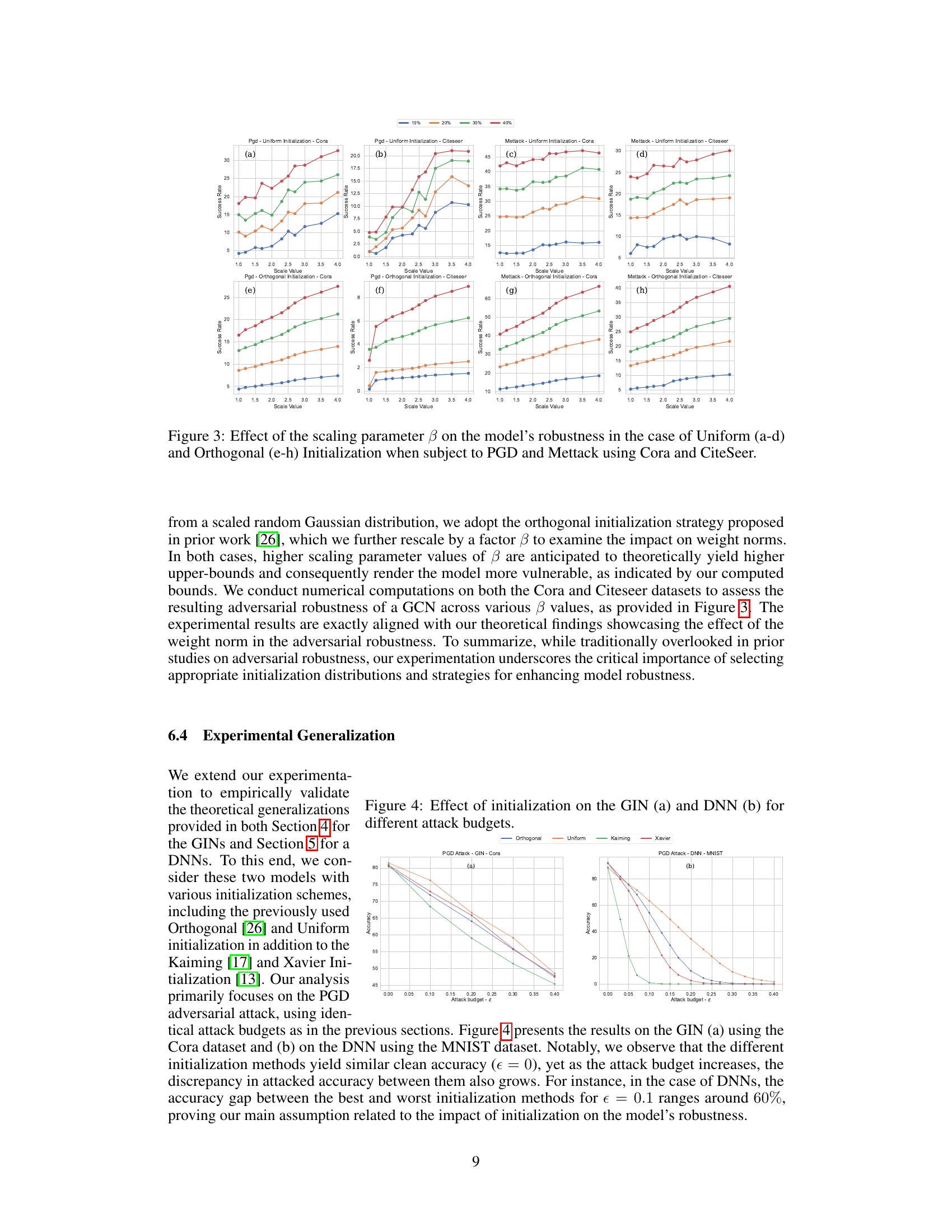
This figure displays the results of experiments evaluating the impact of the variance parameter (σ) of a Gaussian weight initialization on the model’s robustness against adversarial attacks. The experiments are performed using two different attack methods (PGD and Mettack) and on two different datasets (Cora and Citeseer). Each sub-figure shows the success rate of the attacks for different perturbation budgets (10%, 20%, 30%, and 40%). The x-axis represents the value of σ, and the y-axis represents the success rate. The figure shows that increasing the variance generally leads to a higher success rate for the attacks, indicating that the model is less robust when the initial weights have higher variance.

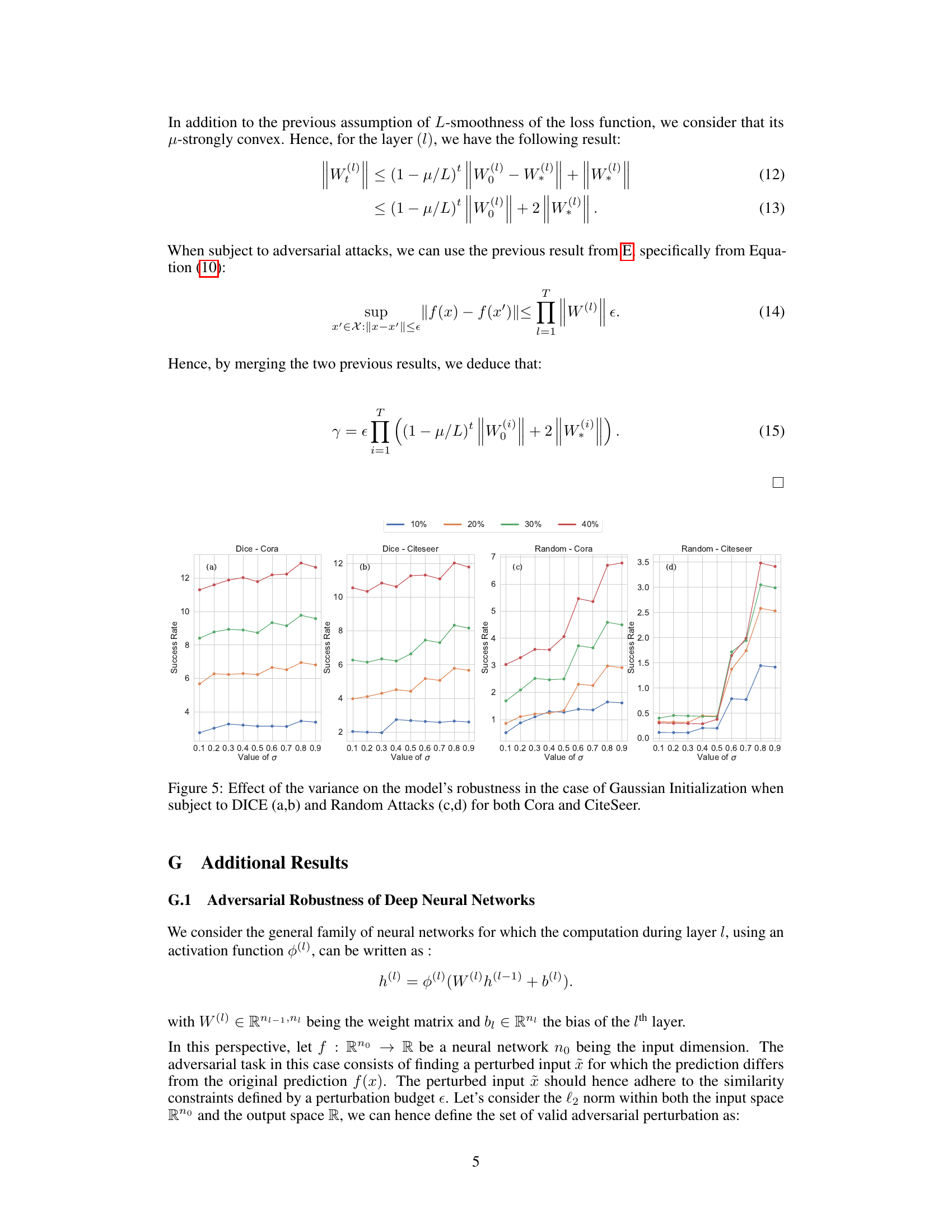
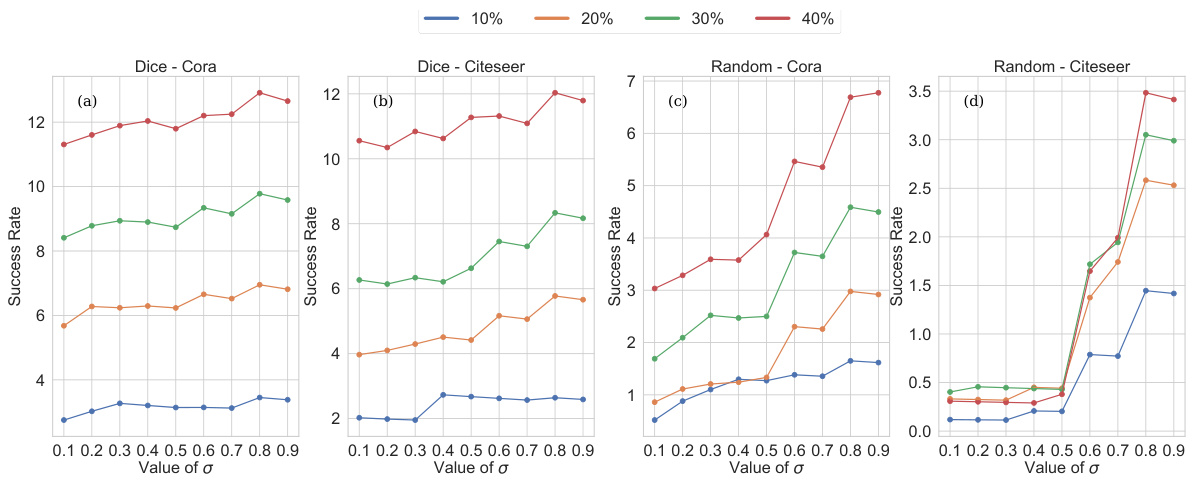
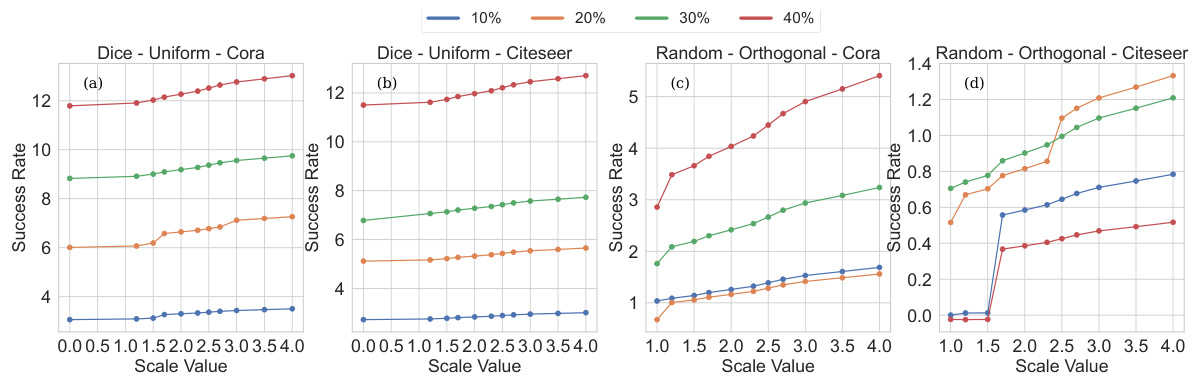
This figure displays the impact of the scaling parameter (β) on the model’s robustness against adversarial attacks when using uniform and orthogonal weight initializations. The plots show success rates (the discrepancy between clean and attacked accuracy) for various attack budgets (10%, 20%, 30%, 40%) on the Cora and Citeseer datasets for both PGD and Mettack attacks. Each subplot shows how success rate changes with the scaling parameter in a specific setting.

This figure shows the impact of the number of training epochs on a GCN’s robustness against adversarial attacks. Subplots (a) and (b) display the results for the Cora dataset, while subplots (c) and (d) present results for the CiteSeer dataset. Each subplot includes two graphs: one showing the clean and attacked accuracy, and the other showing the success rate (difference between clean and attacked accuracy). The results demonstrate a trade-off between clean accuracy and robustness, with increased epochs initially improving clean accuracy but eventually leading to higher vulnerability under attack.
This figure displays the impact of the number of training epochs on a GCN’s robustness against adversarial attacks using the Cora and CiteSeer datasets. Subplots (a) and (b) show the results for Cora, while (c) and (d) present the results for CiteSeer. Each subplot includes two graphs: one showing the clean and attacked accuracy over epochs, and another showing the success rate (difference between clean and attacked accuracy) for different attack budgets (10%, 20%, 30%, 40%). The plots illustrate the trade-off between achieving high clean accuracy and maintaining robustness against attacks as the number of epochs increases.
This figure displays the impact of varying the number of training epochs on the robustness of a graph convolutional network (GCN) against adversarial attacks. The plots show the trade-off between clean accuracy (performance on non-attacked data) and attacked accuracy (performance under adversarial attacks) as the number of epochs increases. Subplots (a) and (b) present results for the Cora dataset, while subplots (c) and (d) show results for the CiteSeer dataset. The plots illustrate that while clean accuracy generally improves with more epochs, attacked accuracy initially improves but then plateaus and eventually decreases, highlighting a trade-off between model performance and robustness to attacks.
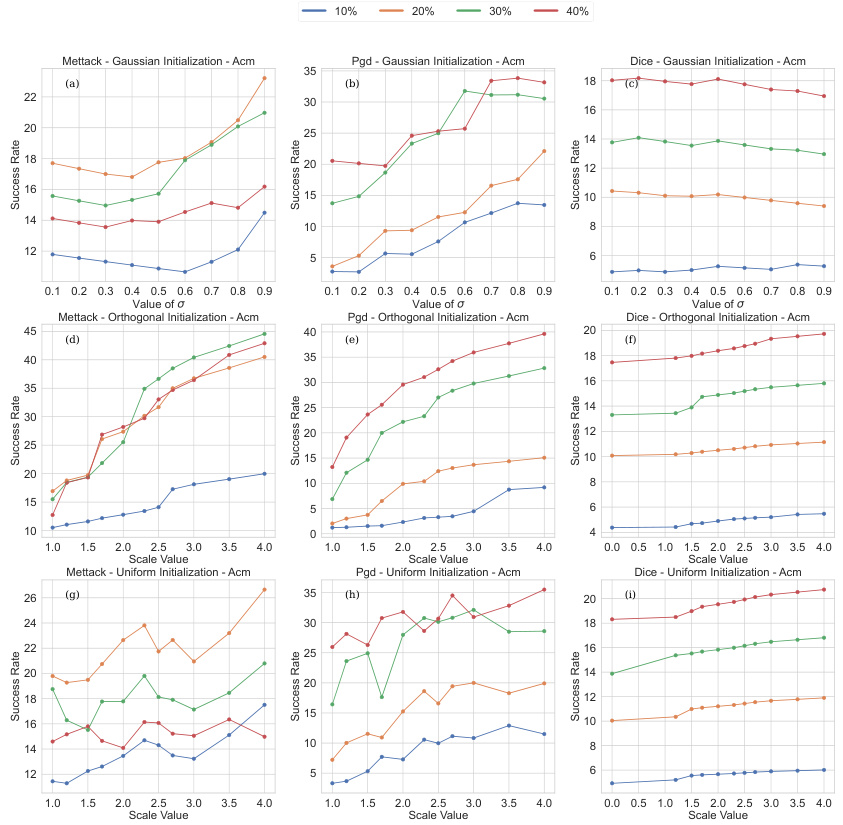
This figure displays the results of experiments conducted to assess the impact of the variance parameter (σ) in a Gaussian weight initialization on model robustness against adversarial attacks. Two adversarial attack methods were employed: PGD and Mettack. The experiments were performed on two datasets: Cora and CiteSeer. For each dataset and attack method, the success rate of the attack across varying values of σ is shown. The success rate represents the discrepancy between the clean and attacked accuracy for a given attack budget. This visualizes the relationship between the variance in initial weights and the robustness of the model.
This figure displays the impact of the number of training epochs on a GCN’s robustness against adversarial attacks. Subplots (a) and (b) show the results for the Cora dataset, while (c) and (d) show the results for the CiteSeer dataset. Each subplot includes two graphs: one showing clean and attacked accuracy and another showing the success rate of the attack (difference between clean and attacked accuracy). The results demonstrate a trade-off between clean accuracy and robustness as the number of epochs increases. Initially, both clean and attacked accuracy rise, but at a certain point, continued training results in reduced robustness, despite improved clean accuracy.

This figure displays the impact of the number of training epochs on a graph convolutional neural network’s (GCN) robustness against adversarial attacks. Subplots (a) and (b) show the results for the Cora dataset, while (c) and (d) show the results for the CiteSeer dataset. Each subplot contains two graphs. The top graph shows the clean accuracy and attacked accuracy as the number of epochs increases. The bottom graph shows the success rate of adversarial attacks, which is the difference between the clean accuracy and attacked accuracy, for various attack budgets. The figure demonstrates that a trade-off exists between clean accuracy and robustness to adversarial attacks: Increasing the number of training epochs increases clean accuracy but decreases adversarial robustness.
Full paper#