↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph neural networks (GNNs) are powerful tools for processing relational data. However, they suffer from a significant limitation known as oversmoothing—a phenomenon where node features become too similar as the network’s depth increases. This limits the creation of deep GNNs which are essential for capturing complex relationships in data. Existing solutions to mitigate this problem often involve complex heuristics.
This research introduces a new theoretical framework for understanding oversmoothing in GNNs. The researchers leverage the Gaussian process equivalence of GNNs in the limit of infinite hidden features and identify a previously unknown non-oversmoothing phase. They demonstrate that by increasing the variance of the initial network weights, GNNs can avoid oversmoothing and maintain informative features even with many layers. This finding is supported by experiments conducted using both synthetic and real-world datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the prevailing belief that graph neural networks (GNNs) inevitably oversmooth, hindering the development of deep and effective models. By introducing a novel non-oversmoothing phase and offering a solution to control oversmoothing, it significantly advances GNN research and opens exciting avenues for improving their performance in various applications.
Visual Insights#
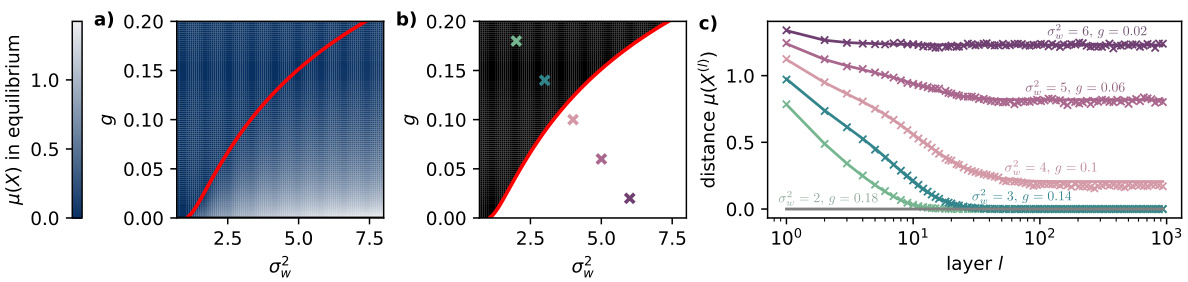
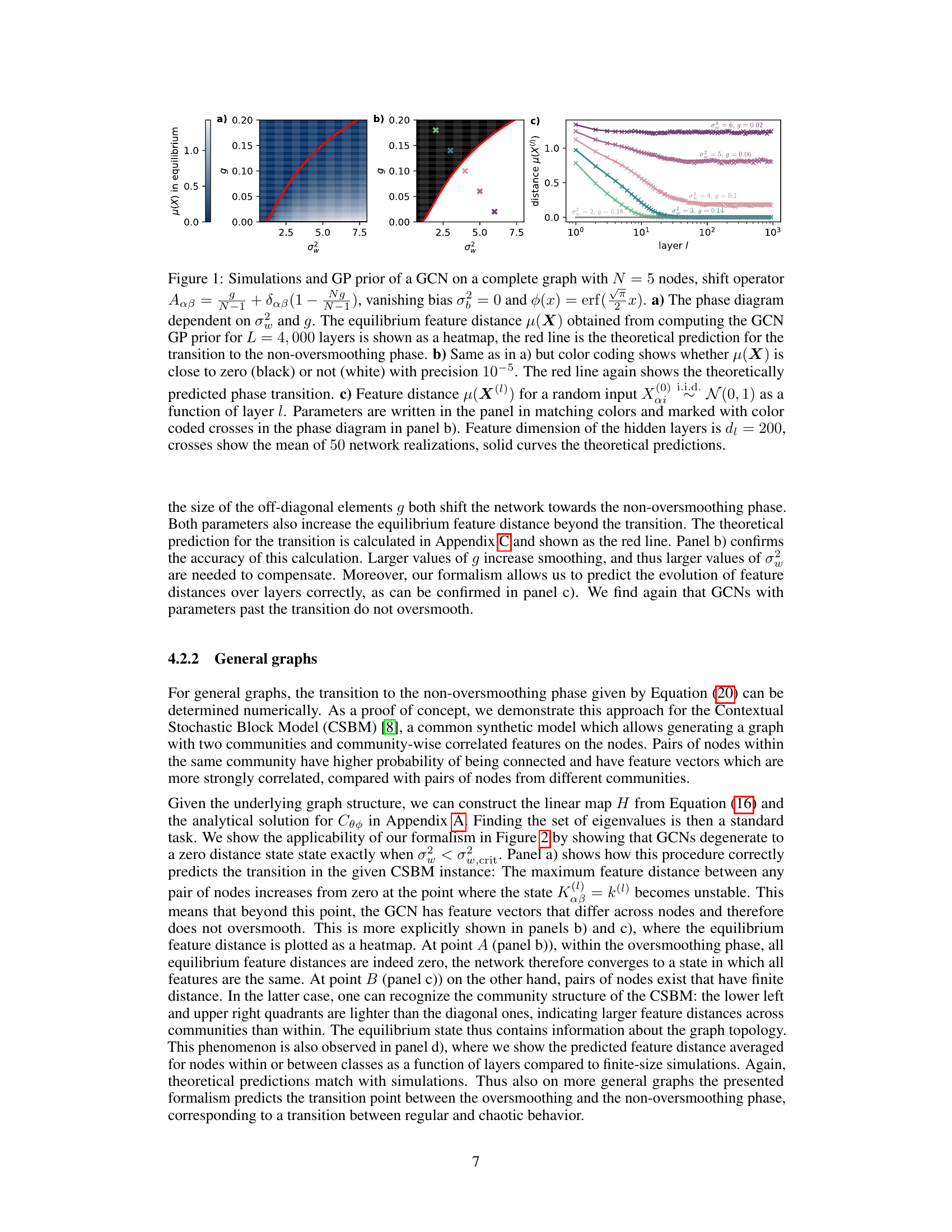
This figure shows a phase diagram for a graph convolutional network (GCN) on a complete graph with 5 nodes. The phase diagram shows the equilibrium feature distance as a function of the weight variance (σ2w) and a parameter (g) that controls the balance between diagonal and off-diagonal elements in the shift operator. The red line indicates the theoretical prediction for the transition to a non-oversmoothing phase, where the feature distances remain informative even at large depths. The figure also includes plots showing the evolution of feature distance with the number of layers for different parameter choices.
In-depth insights#
Overssmoothing Phase#
The concept of an ‘Oversmoothing Phase’ in graph neural networks (GNNs) highlights a critical limitation where, as the network deepens, node feature representations converge, losing crucial information. This phase is characterized by an exponential decay in the distinguishing features between nodes. The paper investigates the conditions under which this occurs, revealing a critical transition point dependent on the initialization of network weights, specifically their variance. Exceeding a threshold variance leads to a ‘chaotic’ phase, avoiding oversmoothing, and maintaining diverse node representations. This suggests the possibility of training significantly deeper and more expressive GNNs by carefully controlling the initialization of weight variance, effectively manipulating the phase transition to prevent convergence and preserve valuable node information.
GCN Propagation#
GCN propagation, the process by which information flows through layers in a graph convolutional network (GCN), is crucial to understanding GCN behavior. Oversmoothing, where node features converge to homogeneity across layers, is a significant challenge, hindering the ability to build deep and expressive GCNs. This phenomenon is closely tied to the eigenvalues of the GCN’s propagation matrix, with eigenvalues close to 1 contributing to slower information decay and increased oversmoothing. Conversely, larger weight variance during initialization can promote a chaotic, non-oversmoothing regime, allowing information to propagate effectively through many layers. The concept of propagation depth helps to quantify this information flow, showing divergence at the critical point between oversmoothing and chaos. Therefore, strategic initialization near this critical point offers the possibility of building both deep and expressive GCNs, maximizing the network’s capability for relational data processing.
Weight Variance#
The concept of ‘weight variance’ in the context of graph neural networks (GNNs) is crucial for understanding and mitigating the problem of oversmoothing. High weight variance can lead to a chaotic phase where node features remain distinct across layers, preventing oversmoothing and allowing the training of deeper, more expressive networks. Conversely, low weight variance results in a regular phase, where oversmoothing occurs as node features converge. The transition between these phases is characterized by a divergence in information propagation depth, implying that carefully tuning the weight variance, particularly by initializing near the transition point, can significantly improve GNN performance, enabling deep architectures without losing informative features. This theoretical analysis, validated by both Gaussian process equivalence and finite-size GCN experiments, highlights the significance of weight initialization as a pivotal aspect in GNN training and design.
Deep GCNs#
The concept of “Deep GCNs” tackles the challenge of overcoming the limitations of shallow Graph Convolutional Networks (GCNs). Shallow GCNs, while effective, struggle to capture long-range dependencies within graph data. Deepening GCNs, however, introduces the problem of oversmoothing, where node feature representations converge to a similar state across layers, hindering the model’s ability to discriminate between nodes. Research in this area focuses on developing techniques to mitigate oversmoothing, such as novel weight initialization strategies, architectural modifications (like residual connections or attention mechanisms), and the use of non-linear activation functions to prevent information loss. The goal is to harness the power of deep learning on graph data by enabling the design and training of expressive deep GCNs that can effectively capture complex relational information in various applications.
Future Work#
The paper’s ‘Future Work’ section would likely explore extending the theoretical framework to encompass a wider range of GNN architectures beyond GCNs, such as Graph Attention Networks (GATs) or other message-passing neural networks. Investigating the impact of different non-linearities on the oversmoothing phenomenon is another crucial area. Furthermore, the efficacy of the proposed initialization strategy for training extremely deep, expressive GNNs should be rigorously tested on more complex real-world datasets, and benchmarking against state-of-the-art methods would be essential to validate its practical value. Finally, delving into the theoretical analysis of finite-size GCNs, moving beyond the infinite-width Gaussian Process limit, will be critical to bridge the gap between theory and practice. This could involve exploring how the dynamics of feature propagation are affected by the number of hidden units. Addressing the computational cost of the eigenvalue calculation for larger graphs is vital to make the approach scalable to real-world applications.
More visual insights#
More on figures
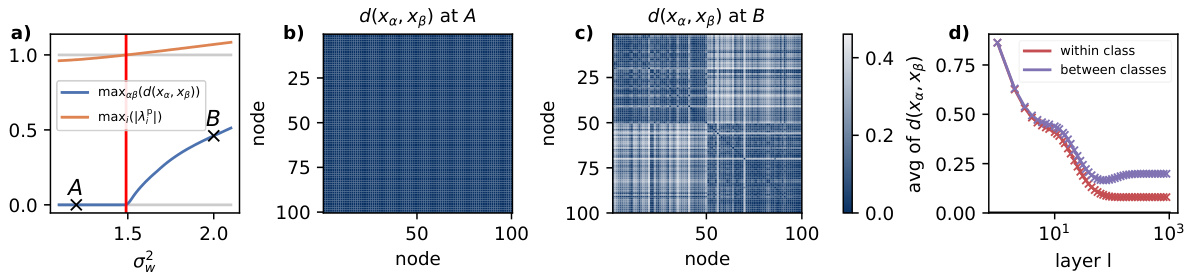
This figure shows an analysis of the non-oversmoothing phase in a contextual stochastic block model. Panel a) shows the transition point between oversmoothing and non-oversmoothing phases, determined by the maximum feature distance and the largest eigenvalue of the linearized GCN GP dynamics. Panels b) and c) visualize the equilibrium distance matrices at different points (A and B) in the phase diagram. Panel d) shows the average feature distance over layers for finite-size GCNs, comparing within-class and between-class distances. The results illustrate how the non-oversmoothing phase is reached by tuning the weight variance, leading to informative features even in deep GCNs.

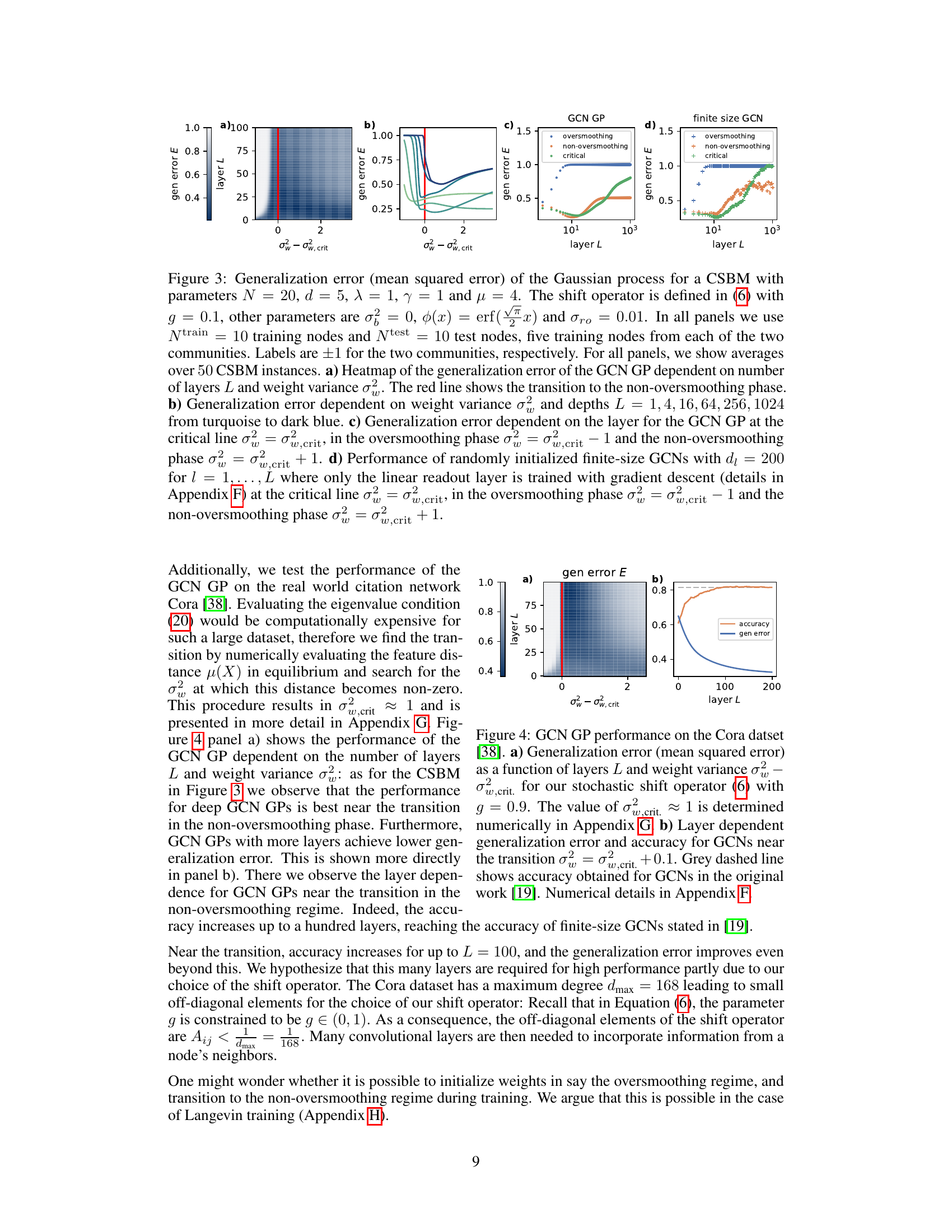
This figure shows the generalization error of Gaussian process for a Contextual Stochastic Block Model (CSBM) with different parameters, specifically focusing on the impact of weight variance (σ²) and the number of layers (L) on the generalization performance. The figure is divided into four subplots, each demonstrating a different aspect of the relationship between these parameters and generalization error. It also compares the performance of Gaussian Process (GP) and finite-size Graph Convolutional Networks (GCNs).
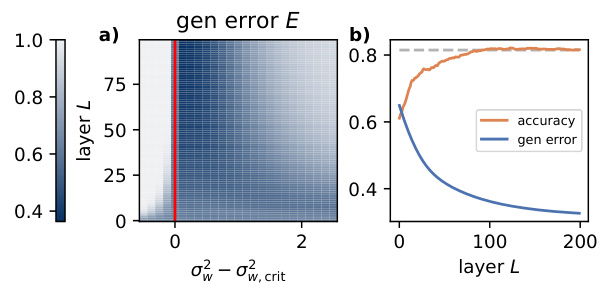
This figure shows the generalization error of Gaussian process for a Contextual Stochastic Block Model (CSBM) with different parameters. It demonstrates how the generalization error changes with the number of layers and weight variance. The figure also highlights the transition point between oversmoothing and non-oversmoothing phases.
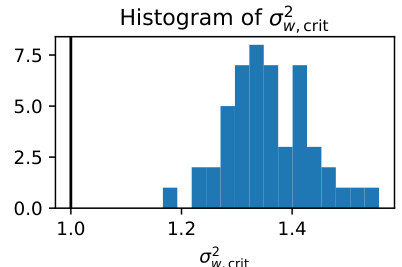
This histogram visualizes the distribution of critical weight variances (σ2w,crit) obtained from 50 simulations of the Contextual Stochastic Block Model (CSBM) used in the experiments of Figure 3. Each critical weight variance represents the threshold beyond which the graph convolutional network (GCN) transitions from an oversmoothing to a non-oversmoothing phase. The vertical line at σ2w,crit = 1 is included for comparison with results found in related research. The distribution shows that many of the critical variances are above 1, indicating that oversmoothing can be avoided by initializing the weight variance beyond a certain threshold.
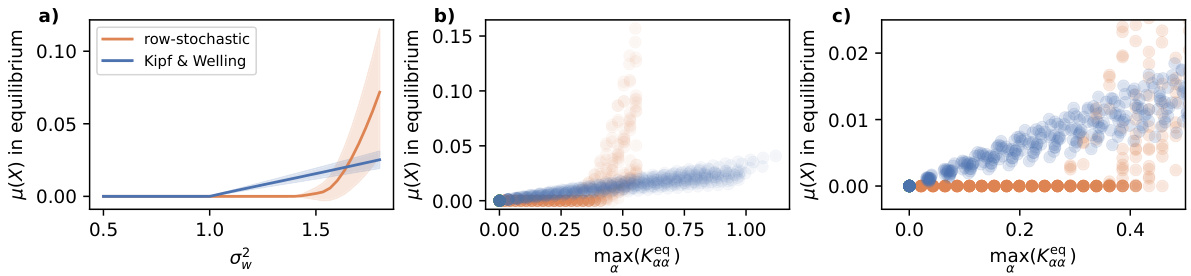
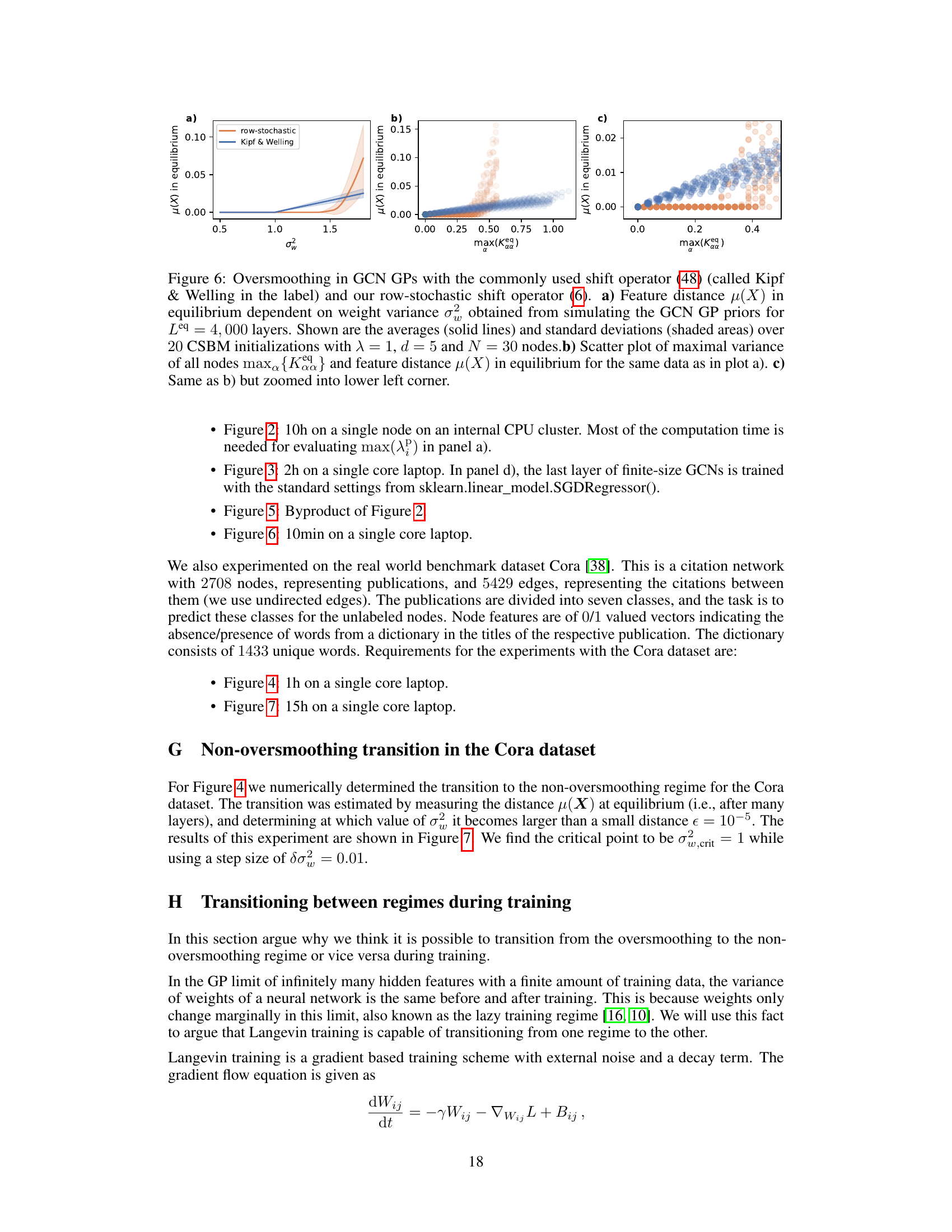
This figure compares the oversmoothing behavior of GCNs using two different shift operators: a row-stochastic operator and the commonly used Kipf & Welling operator. Panel (a) shows the equilibrium feature distance (μ(X)) as a function of weight variance (σw2). Panels (b) and (c) present scatter plots relating the equilibrium feature distance to the maximum variance among nodes, offering a closer look at the transition between oversmoothing and non-oversmoothing phases.

This figure shows the equilibrium node distance (μ(X)) as a function of weight variance (σw2) obtained from a Gaussian process approximation of a graph convolutional network (GCN) with 4000 layers. The red line marks the transition point to the non-oversmoothing regime, where the equilibrium node distance becomes greater than a small threshold (∈ = 10⁻⁵). This demonstrates how increasing weight variance leads to a phase transition where the GCN no longer oversmooths.
Full paper#