TL;DR#
Real-world image denoising is challenging due to the complex and unpredictable nature of real-world noise, unlike artificial noise like AWGN. Existing methods often struggle to generalize well from training data to real-world scenarios, often requiring paired noisy-clean datasets which are expensive and difficult to obtain. Self-supervised methods offer a solution, but their performance is often limited by the difficulty of handling noise correlation in real images.
SelfFormer addresses these issues with a novel approach. It uses a transformer-based architecture with a directional self-attention mechanism to effectively capture long-range dependencies between pixels and mitigate the impact of noise correlation. This, combined with a pseudo-Siamese network for mutual learning and a gridding scheme for efficiency, leads to significant improvements in real-world image denoising. The method outperforms existing self-supervised and clean-image-free methods on benchmark datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel self-supervised method for real-world image denoising, outperforming existing methods. Its use of transformers and a unique directional self-attention mechanism offers a new approach to handling noise correlation in real images. This opens avenues for further research into self-supervised learning and transformer applications in low-level vision tasks. The proposed method’s efficiency compared to other transformer-based methods is also a significant contribution.
Visual Insights#

🔼 This figure illustrates the core idea behind the proposed Directional Self-Attention (DSA) mechanism. Panel (a) shows standard self-attention (SA), where the attention window encompasses all pixels. In contrast, panel (b) depicts the DSA mechanism. Here, the attention window is restricted to a half-plane, preventing the current token from attending to itself, thus creating a ‘blind spot’ This blind spot is crucial for self-supervised learning, as it prevents the network from trivially learning the identity mapping. The figure showcases several attention windows to emphasize how the half-plane grid is dynamically applied to each token.
read the caption
Figure 1: Illustration of basic idea of our approach.

🔼 This table presents a comparison of the performance of various image denoising methods on three benchmark datasets: SIDD, DND, and NIND. The methods are categorized into supervised, unsupervised, zero-shot, and self-supervised approaches. The table shows PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity Index) scores for each method and dataset. The best performing methods that do not use clean images are highlighted in bold.
read the caption
Table 1: PSNR(dB)/SSIM results on SIDD benchmark, DND benchmark and NIND dataset. We report the official results from the benchmarks' websites whenever possible. The results of Zhou et al.are quoted from [27]. The results of Noise2Void and Noise2Self are quoted from [45]. The results of DnCNN and Laine et al.are obtained by code re-running. Bold denotes the best results in clean-image-free methods.
In-depth insights#
Blind-Spot Transformer#
The concept of a ‘Blind-Spot Transformer’ blends the strengths of transformer networks with the blind-spot mechanism commonly found in self-supervised denoising methods. Transformers excel at capturing long-range dependencies, crucial for effective denoising where noise correlation across distant pixels must be addressed. The blind-spot approach, however, introduces a constraint by preventing the network from directly observing the pixel it aims to reconstruct; this clever trick forces the network to learn from the contextual information surrounding the blind spot, mitigating overfitting. This combination is powerful because it harnesses the transformer’s ability to effectively integrate global information while avoiding the pitfall of trivial solutions. A key design consideration would involve architecting the attention mechanism to selectively mask relevant input features, effectively creating the blind spot without hindering the model’s capacity for long-range interactions. A directional self-attention module might be an ideal candidate, focusing attention within a half-plane, thus ensuring the central pixel remains effectively hidden while neighboring pixels are considered. Further research could investigate optimal grid sizes and patterns within the attention mechanism to balance computational costs and performance.
Self-Supervised Denoising#
Self-supervised denoising tackles the challenge of image denoising using only noisy images, eliminating the need for paired clean-noisy datasets. This is crucial because obtaining such datasets is often expensive and time-consuming. The core idea is to train a neural network to learn the underlying clean image representation from the noisy input alone, often leveraging clever architectural designs like blind-spot networks or specific loss functions. Blind-spot networks, for instance, cleverly prevent the network from simply memorizing the input by masking or excluding the central pixel during training, forcing it to learn from the surrounding context. This field is actively exploring novel network architectures, especially transformers, to capture long-range dependencies within images and further enhance denoising performance. Despite significant advancements, self-supervised approaches still face challenges in dealing with real-world noise, which is complex and differs substantially from synthetic noise. Future research will likely focus on more robust architectures that handle real-world noise’s variability, potentially using generative models and improved loss functions to better guide the learning process.
Directional Self-Attention#
Directional self-attention, as a novel mechanism, offers a compelling approach to enhance the performance of self-supervised real-world image denoising. By restricting the attention window to a half-plane, it cleverly introduces a blind-spot structure, preventing the network from trivial solutions and promoting effective noise removal. This directional constraint is crucial for handling real-world noise, which unlike artificial noise (e.g. AWGN), often exhibits complex spatial correlations. The integration of a gridding scheme further boosts computational efficiency, making the method scalable for practical applications. Unlike conventional full-attention mechanisms, this approach avoids masking input pixels, preserving the integrity and accuracy of long-range feature interactions. The pseudo-Siamese architecture acts as a powerful regularizer, mitigating potential negative impacts from the restricted attention grid, ultimately improving the overall denoising performance.
Siamese Architecture#
The utilization of a Siamese architecture in this research paper presents a compelling approach to enhance the performance of the directional self-attention (DSA) module. The inherent limitation of DSA, its restricted attention grid, is cleverly mitigated by incorporating a second sub-network employing full-grid self-attention. This pairing facilitates a pseudo-Siamese structure where the two networks, one with directional and the other with full attention, learn collaboratively. The resulting mutual regularization, stemming from the comparison of outputs of these two contrasting network branches, effectively addresses the shortcomings of restricted attention in DSA. This synergy is crucial for leveraging the strengths of both approaches, harnessing the long-range dependencies captured by full-grid attention while retaining the blind-spot mechanism facilitated by DSA. The pseudo-Siamese setup is particularly beneficial during training, preventing the restricted-attention DSA network from collapsing into an identity mapping. Ultimately, this architecture not only enhances the model’s accuracy but also enhances its generalizability and robustness, leading to improved real-world denoising performance.
Future Enhancements#
Future enhancements for this self-supervised real-world image denoising method could explore several avenues. Improving the efficiency of the transformer architecture is crucial, potentially through exploring more lightweight attention mechanisms or optimizing the computational cost of the directional self-attention module. Expanding the dataset used for training would significantly improve generalization capabilities. The incorporation of additional datasets with diverse noise characteristics and imaging conditions would enhance the robustness and real-world applicability. Furthermore, investigating the integration of other deep learning components, such as generative models or advanced regularization techniques, might lead to more refined denoising results. Exploring different loss functions beyond the current self-reconstruction and mutual learning losses could further optimize performance. Finally, a thorough qualitative and quantitative evaluation on a wider range of real-world noisy images is necessary to fully assess the effectiveness and limitations of the proposed method.
More visual insights#
More on figures
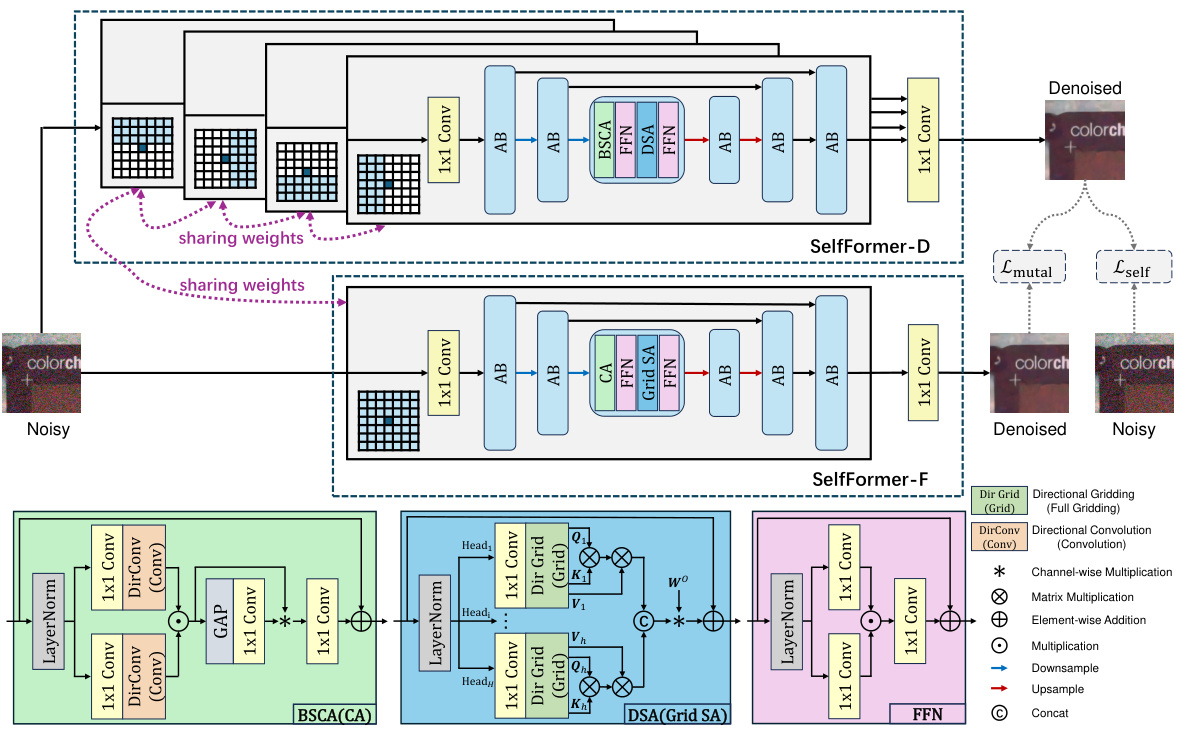
🔼 The figure shows the architecture of the proposed SelfFormer, which consists of two sub-networks: SelfFormer-D and SelfFormer-F. SelfFormer-D has four branches, each using directional self-attention (DSA) with a half-plane grid, creating a blind-spot structure. SelfFormer-F uses full-grid self-attention (SA) with a single branch. Both sub-networks share weights, except for the last 1x1 convolution. The figure also details the components of each attention block, including channel attention (CA or BSCA), feed-forward networks (FFN), and DSA/grid SA modules. The overall loss function combines self-reconstruction and mutual learning losses to improve performance.
read the caption
Figure 3: Architecture of the proposed SelfFormer.

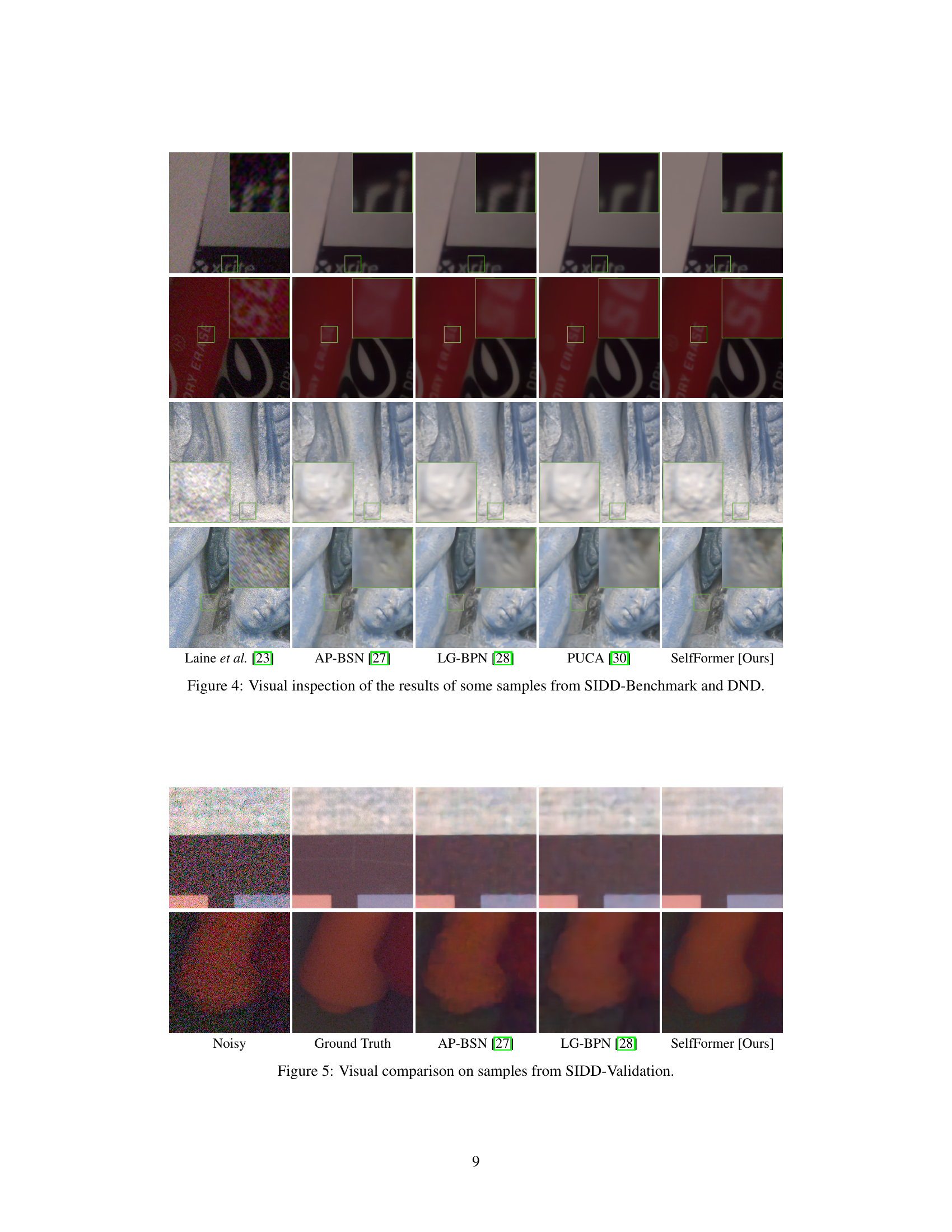
🔼 This figure shows a visual comparison of denoising results from several methods on samples from SIDD-Benchmark and DND datasets. The top two rows show results for images with relatively flat regions, while the bottom two rows show results for images with more textured regions. Each column represents a different denoising method: Laine et al. [23], AP-BSN [27], LG-BPN [28], PUCA [30], and SelfFormer (Ours). The green boxes highlight specific regions for closer examination and comparison of the results.
read the caption
Figure 4: Visual inspection of the results of some samples from SIDD-Benchmark and DND.
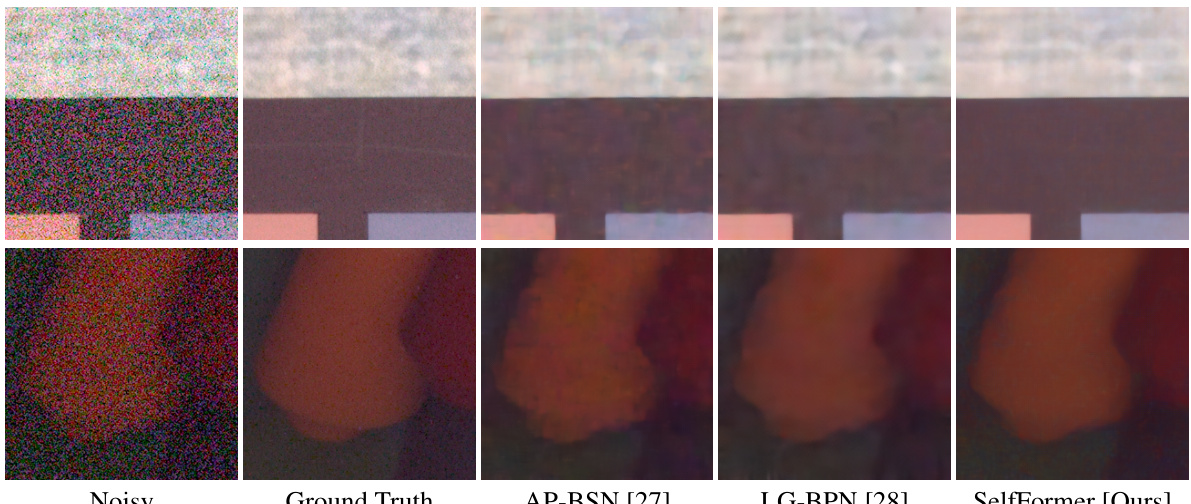
🔼 This figure shows a visual comparison of denoising results from different methods on samples from the SIDD-Benchmark dataset. It specifically highlights the performance on images with richly textured regions, allowing for a detailed comparison of the preservation of fine details and the handling of noise by each algorithm.
read the caption
Figure A3: More qualitative comparison on samples from SIDD-Benchmark.

🔼 This figure shows a qualitative comparison of denoising results from several methods on samples from the SIDD-Benchmark and DND datasets. Each row represents a different image, and each column shows the results obtained using a different denoising method, including Laine et al. [23], AP-BSN [27], LG-BPN [28], PUCA [30], and the proposed SelfFormer. The green boxes highlight specific regions of interest where differences between the methods are most apparent. The figure is intended to show the visual differences and improvement provided by the proposed SelfFormer.
read the caption
Figure 4: Visual inspection of the results of some samples from SIDD-Benchmark and DND.

🔼 This figure provides a visual comparison of the denoising results from several methods on samples from the SIDD-Benchmark dataset. It shows the noisy input images, the ground truth clean images, and the denoised outputs produced by different methods, including Laine et al., AP-BSN, LG-BPN, PUCA and the proposed SelfFormer. This allows for a direct visual comparison of the performance of each method in handling complex real-world noise.
read the caption
Figure A3: More qualitative comparison on samples from SIDD-Benchmark.

🔼 This figure shows a visual comparison of denoising results from several methods on samples from the SIDD-Benchmark and DND datasets. The top row shows denoising results from Laine et al. [23], AP-BSN [27], LG-BPN [28], PUCA [30], and SelfFormer (Ours) on a sample from SIDD-Benchmark. The middle row shows the same comparison on a sample from the DND dataset. The bottom row is another SIDD-Benchmark sample. Each method’s performance is visually assessed by comparing its output to the original, noisy image.
read the caption
Figure 4: Visual inspection of the results of some samples from SIDD-Benchmark and DND.
More on tables

🔼 This table presents a comparison of the performance of various image denoising methods on three benchmark datasets: SIDD, DND, and NIND. The methods are categorized into several groups based on their training approach (supervised with synthetic or real pairs, unsupervised, zero-shot, and self-supervised) and whether they require clean images during training. The performance is measured using PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity Index). The table highlights the best-performing methods that do not use clean images during training, demonstrating the effectiveness of self-supervised approaches.
read the caption
Table 1: PSNR(dB)/SSIM results on SIDD benchmark, DND benchmark and NIND dataset. We report the official results from the benchmarks' websites whenever possible. The results of Zhou et al.are quoted from [27]. The results of Noise2Void and Noise2Self are quoted from [45]. The results of DnCNN and Laine et al.are obtained by code re-running. Bold denotes the best results in clean-image-free methods.

🔼 This table compares the computational complexity of different self-supervised denoising methods in terms of model size (number of parameters) and inference time for a 256x256 image. It shows that SelfFormer-F has a smaller model size and significantly faster inference time compared to other transformer-based methods (LG-BPN and SS-BSN). It also shows that SelfFormer-F is comparable to the best-performing CNN-based method (PUCA) in terms of performance while being much faster.
read the caption
Table 2: Computational complexity comparison in terms of model size and inference time.

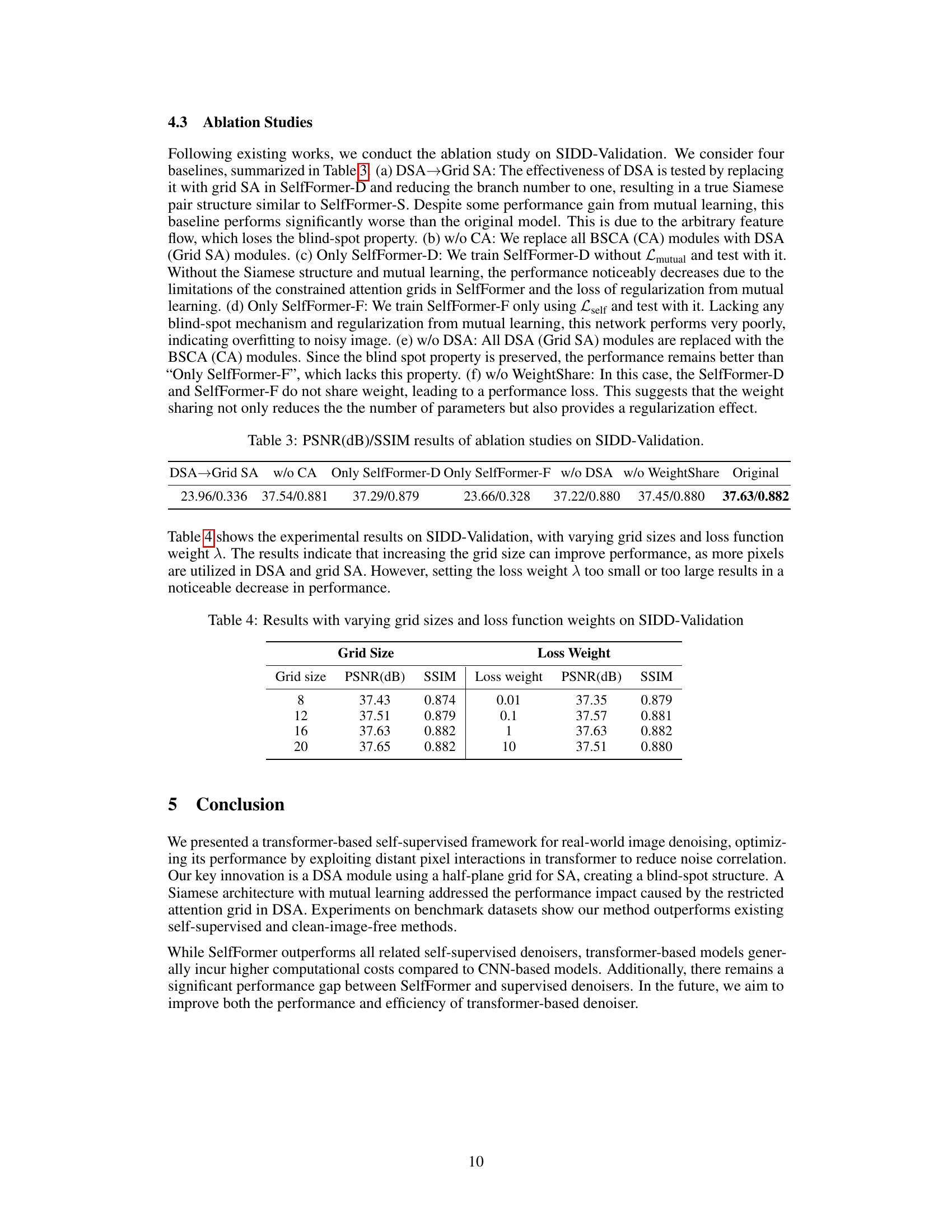
🔼 This table presents the results of ablation studies conducted on the SIDD-Validation dataset to evaluate the impact of different components of the proposed SelfFormer model. The base model’s performance is compared against versions where key components like Directional Self-Attention (DSA), Channel Attention (CA), and the Siamese architecture are removed or replaced. This allows for assessing the individual contribution of each part to the overall denoising performance.
read the caption
Table 3: PSNR(dB)/SSIM results of ablation studies on SIDD-Validation.
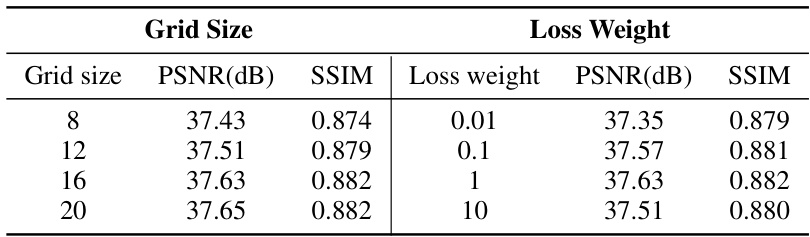
🔼 This table presents the ablation study results on the SIDD-Validation dataset. It shows the impact of varying the grid size used in the directional self-attention (DSA) and grid self-attention (Grid SA) modules, and the impact of varying the loss function weight (lambda) in the overall loss function (Ltotal = Lself + lambda*Lmutual). The results demonstrate how different grid sizes and loss weights affect the model’s performance measured by PSNR and SSIM.
read the caption
Table 4: Results with varying grid sizes and loss function weights on SIDD-Validation

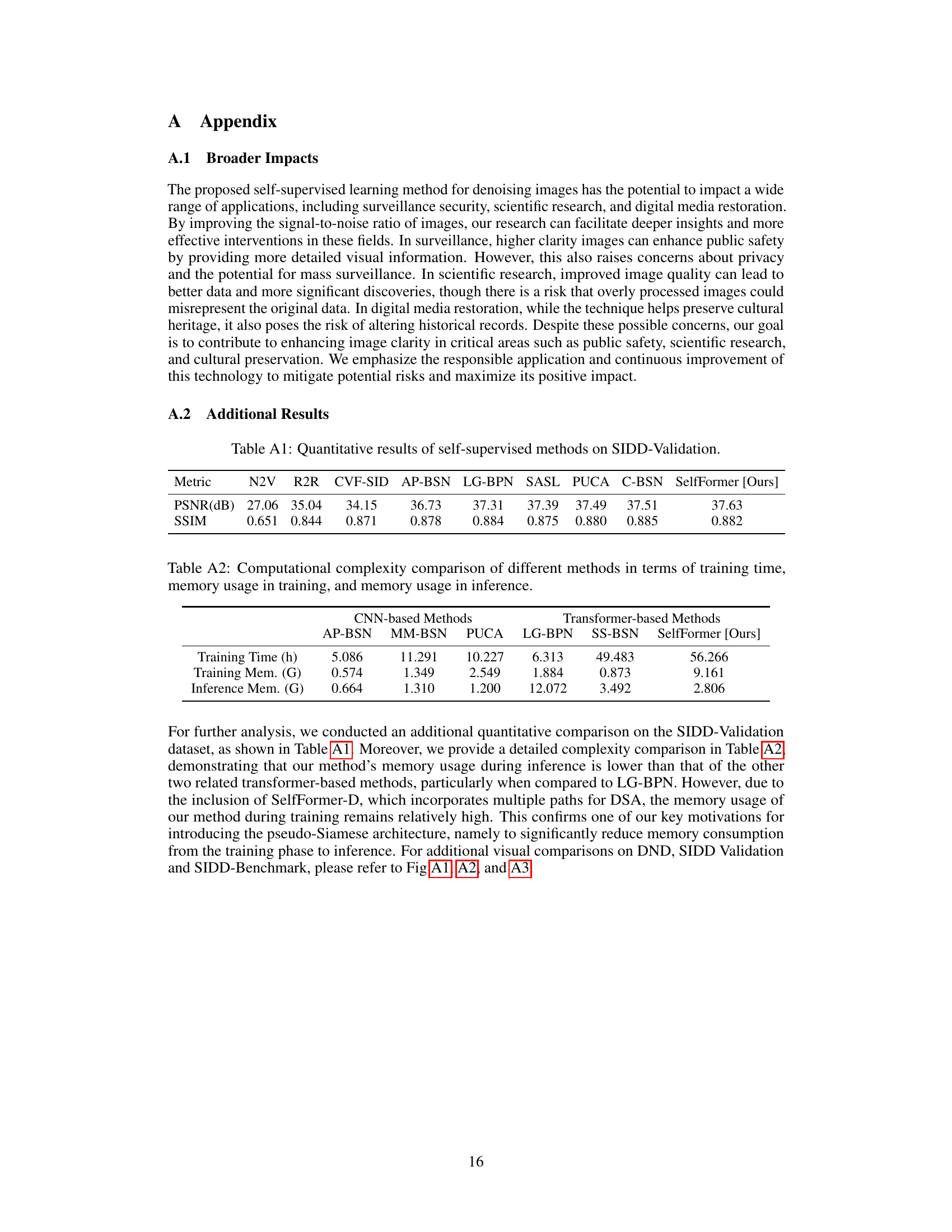
🔼 This table presents a comparison of the performance of various self-supervised image denoising methods on the SIDD-Validation dataset. The metrics used for comparison are PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity Index). The methods compared include Noise2Void (N2V), Recorrupted2Recorrupted (R2R), CVF-SID, AP-BSN, LG-BPN, SASL, PUCA, C-BSN, and the proposed SelfFormer method. Higher PSNR and SSIM values indicate better denoising performance.
read the caption
Table A1: Quantitative results of self-supervised methods on SIDD-Validation.

🔼 This table presents a comparison of the computational complexity among different image denoising methods. It specifically contrasts the model size (number of parameters) and inference time for a 256x256 image across various CNN-based and transformer-based approaches. This allows for a quantitative assessment of the efficiency and resource requirements of each method.
read the caption
Table 2: Computational complexity comparison in terms of model size and inference time.
Full paper#