↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many statistical tasks require sampling from probability distributions, often only defined up to a normalization constant. Existing methods struggle when additional constraints are imposed, such as those ensuring fairness or robustness. These constraints are often handled by post-processing, penalties or transformations, each with limitations in efficiency and applicability.
This work introduces Primal-Dual Langevin Monte Carlo (PD-LMC), a novel algorithm that simultaneously enforces constraints and generates samples. PD-LMC leverages gradient descent-ascent dynamics, and provides sublinear convergence rates under common assumptions. The algorithm’s effectiveness is demonstrated via diverse applications, showcasing its superior performance compared to existing methods, particularly in scenarios involving complex, non-linear constraints.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on Bayesian inference, machine learning, and statistics. It offers a novel and effective solution to a long-standing challenge: sampling from distributions under complex constraints, such as fairness or robustness requirements. The proposed algorithm, Primal-Dual Langevin Monte Carlo, is theoretically grounded and practically effective, opening new avenues for research into constrained sampling and its applications.
Visual Insights#

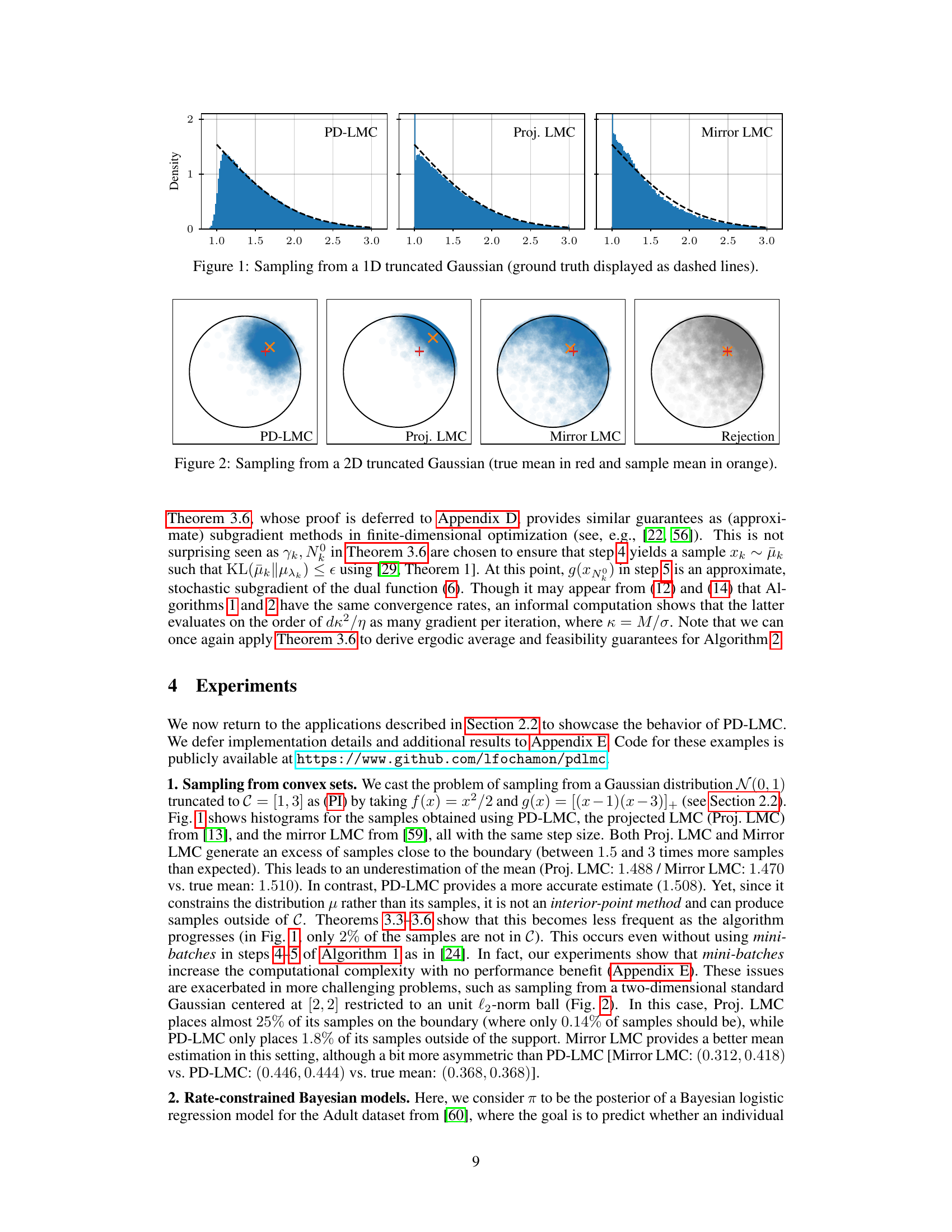
This figure compares the performance of three different algorithms (PD-LMC, Projected LMC, and Mirror LMC) for sampling from a 1D truncated Gaussian distribution. The histograms show the distribution of samples generated by each algorithm, with the ground truth distribution shown as dashed lines. The figure illustrates how PD-LMC, while not perfect, generally performs better than the other algorithms at generating samples from the constrained region, although some samples may still lie outside of it.

The table categorizes different approaches to handling sampling constraints based on whether the constraint is on the samples themselves (hard constraint) or on the distribution of the samples (soft constraint). For hard constraints, methods like mirror/proximal Langevin Monte Carlo, projected Langevin Monte Carlo, and barrier methods are mentioned. For soft constraints, penalized Langevin Monte Carlo is mentioned, and the paper’s proposed method, Primal-Dual Langevin Monte Carlo (PD-LMC), is highlighted.
In-depth insights#
Constrained Sampling#
Constrained sampling tackles the challenge of sampling from a probability distribution while adhering to specified constraints. This contrasts with standard sampling methods that ignore such limitations. The core problem involves finding a distribution that is both close to the target and satisfies the constraints, often using techniques like Kullback-Leibler divergence minimization. This methodology is crucial in various applications, including Bayesian inference, where it can be used to enforce realistic conditions on model parameters or even evaluate counterfactual scenarios. Computational efficiency is a significant concern, particularly when dealing with high-dimensional spaces or complex constraints. There’s a trade-off between the accuracy of satisfying the constraints and how close the resulting distribution remains to the original target. Therefore, it’s important to design algorithms that balance accuracy with efficiency. Advanced techniques, such as primal-dual methods, are often used to solve the constrained optimization problem efficiently. These approaches focus on solving the dual problem, which frequently has better properties, and then utilizing the solution to sample from the desired distribution.
PD-LMC Algorithm#
The Primal-Dual Langevin Monte Carlo (PD-LMC) algorithm is a novel approach to constrained sampling. It cleverly combines gradient descent-ascent dynamics with Langevin Monte Carlo to simultaneously satisfy statistical constraints and sample from a target distribution. This contrasts with existing methods that typically handle constraints through post-processing or penalty terms, often leading to inefficient sampling. The algorithm’s strength lies in its ability to directly incorporate constraints, resulting in more accurate and efficient sampling. Its convergence analysis demonstrates sublinear convergence under standard assumptions on convexity and log-Sobolev inequalities, providing a solid theoretical foundation. PD-LMC avoids explicit integration, making it practical for high-dimensional problems, a significant advantage over existing approaches which may struggle with complex integration steps. The method shows promise in Bayesian inference, fairness-aware machine learning, and counterfactual analysis.
Convergence Analysis#
A rigorous convergence analysis is crucial for establishing the reliability and efficiency of any algorithm. In the context of the provided research paper, this analysis would delve into the theoretical guarantees of the proposed method, likely focusing on the rate at which the algorithm converges to the desired solution. Key aspects would include specifying the assumptions made about the problem’s structure (e.g., convexity, smoothness, and strong convexity conditions of the objective functions and constraints), and proving bounds on the error or distance between the algorithm’s iterates and the true solution. The analysis might employ techniques from optimization theory, probability theory, or differential geometry, depending on the nature of the problem and the algorithm. Furthermore, a comprehensive analysis would discuss the impact of various parameters (e.g., step size, mini-batch size) on the convergence rate, and ideally, provide insights into optimal parameter settings. The convergence analysis also needs to account for stochasticity, as many sampling algorithms involve random elements. Tight bounds and convergence rates are important indicators of the algorithm’s effectiveness. It is also essential to consider the computational complexity in relation to the convergence rate, balancing the speed of convergence with practical limitations.
Empirical Studies#
An ‘Empirical Studies’ section in a research paper would present the experimental validation of the proposed methods. It would detail the datasets used, meticulously describing their characteristics and limitations, the experimental setup, including parameter choices and evaluation metrics. The results would be presented clearly, ideally with visualizations, error bars (to indicate uncertainty), and statistical significance tests. A strong emphasis should be placed on reproducibility, providing sufficient details for others to replicate the experiments. The discussion should critically assess the results, acknowledging limitations and comparing performance against existing baselines. Addressing any unexpected or contradictory findings is essential, along with insights gained into the algorithm’s behavior and potential areas for improvement. Finally, this section needs to directly support the paper’s central claims, showing how the empirical results confirm or challenge the theoretical analysis.
Future Work#
The authors propose several avenues for future research, primarily focusing on strengthening the theoretical foundations and expanding the applicability of their primal-dual Langevin Monte Carlo (PD-LMC) algorithm. Improving convergence rate guarantees is a key goal, especially exploring the use of acceleration or proximal methods to achieve faster convergence, particularly in the log-Sobolev inequality (LSI) setting. Further investigation into the algorithm’s behavior under weaker assumptions and expanding the types of constraints it handles are also mentioned. Addressing the challenges of high-dimensional problems is crucial, including examining whether the current approach scales effectively to larger dimensions and investigating mini-batch techniques to enhance computational efficiency. Finally, more extensive empirical evaluations across diverse applications are planned to further validate the effectiveness of PD-LMC and explore potential improvements and modifications.
More visual insights#
More on figures

This figure compares the performance of three different sampling methods: PD-LMC, Projected LMC, and Mirror LMC, in sampling from a 1D truncated Gaussian distribution. The histograms show the distribution of samples generated by each method. The dashed line represents the true, underlying distribution of the truncated Gaussian. The figure illustrates how the different methods approximate the target distribution with varying degrees of accuracy. PD-LMC shows a good approximation, while Projected LMC and Mirror LMC show a slight deviation, concentrating samples closer to the boundaries of the truncated distribution.
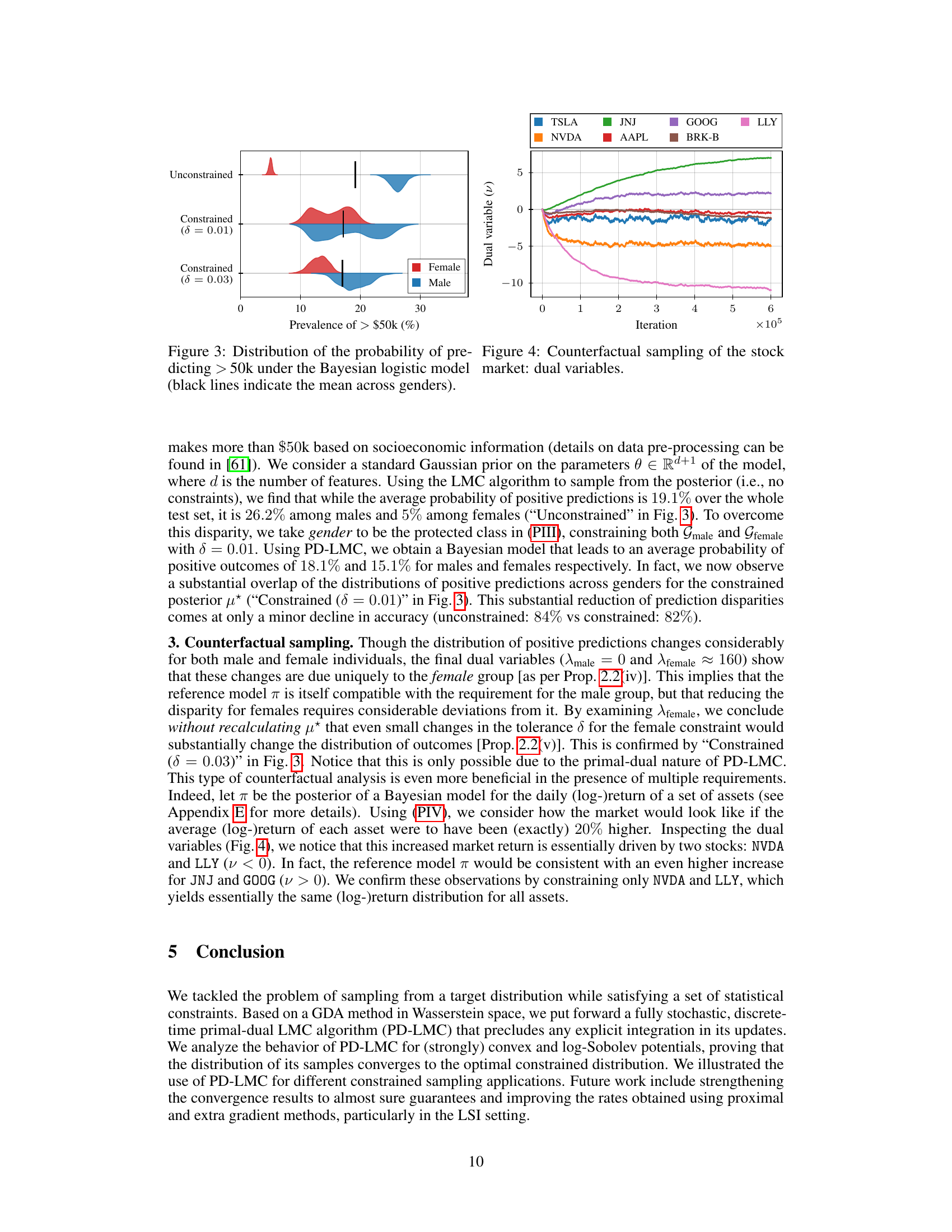
This figure compares the performance of four different sampling methods: PD-LMC, Projected LMC, Mirror LMC, and Rejection sampling, in generating samples from a 2D truncated Gaussian distribution. The true mean is shown in red, and the sample mean is shown in orange for each method. The figure visually demonstrates how each method samples from the distribution and how well they estimate the true mean, providing a visual comparison of their efficiency and accuracy in the context of constrained sampling problems.

This figure displays the distributions of the probability of predicting whether an individual makes more than $50k, obtained from a Bayesian logistic regression model. It shows three different scenarios: unconstrained sampling (no fairness constraints), constrained sampling with a tolerance (δ) of 0.01, and constrained sampling with a tolerance of 0.03. The black lines represent the mean probability for each gender (male and female) in each scenario. The figure visually demonstrates the impact of applying fairness constraints (via constrained sampling) on reducing the disparity between the probability distributions for males and females. As δ increases (more tolerance allowed), the disparity slightly increases.

This figure shows two plots related to one-dimensional truncated Gaussian sampling using the Primal-Dual Langevin Monte Carlo (PD-LMC) algorithm. Plot (a) displays the ergodic average of the constraint function (slack), which measures how well the algorithm satisfies the constraints over time. Plot (b) shows the evolution of the dual variable λ, which is a parameter used in the algorithm to enforce constraints. The convergence of the constraint slack toward zero and the convergence of the dual variable to a stable value indicate successful constraint satisfaction.

This figure demonstrates the impact of mini-batch size (Nь) on the performance of the Primal-Dual Langevin Monte Carlo (PD-LMC) algorithm when sampling from a one-dimensional truncated Gaussian distribution. It shows two subfigures: (a) plots the estimated mean against the number of PD-LMC iterations, and (b) plots the estimated mean against the number of Langevin Monte Carlo (LMC) evaluations. Different lines represent different mini-batch sizes, highlighting how the choice of Nь affects the convergence rate and computational cost of the algorithm. The true mean is shown as a dashed line for reference.

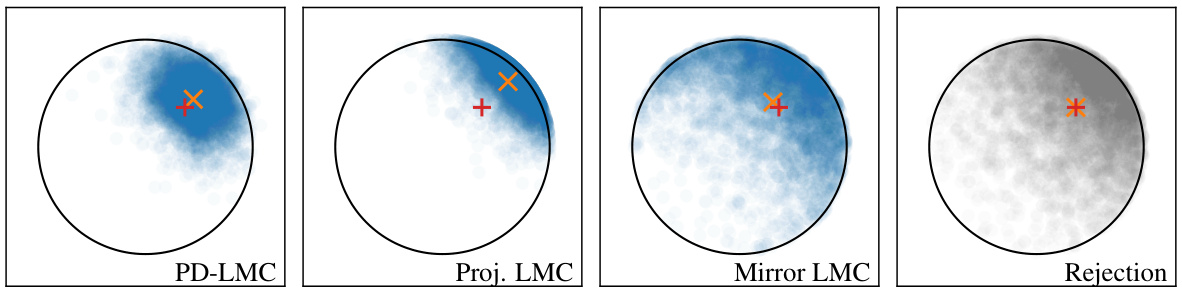
This figure compares the density estimates of samples generated by Projected Langevin Monte Carlo (Proj. LMC) and Primal-Dual Langevin Monte Carlo (PD-LMC) for a two-dimensional truncated Gaussian distribution. It visually demonstrates the difference in sample distribution between these two methods, especially near the boundary of the truncated region. PD-LMC shows better performance at keeping samples within the desired region than Proj. LMC.
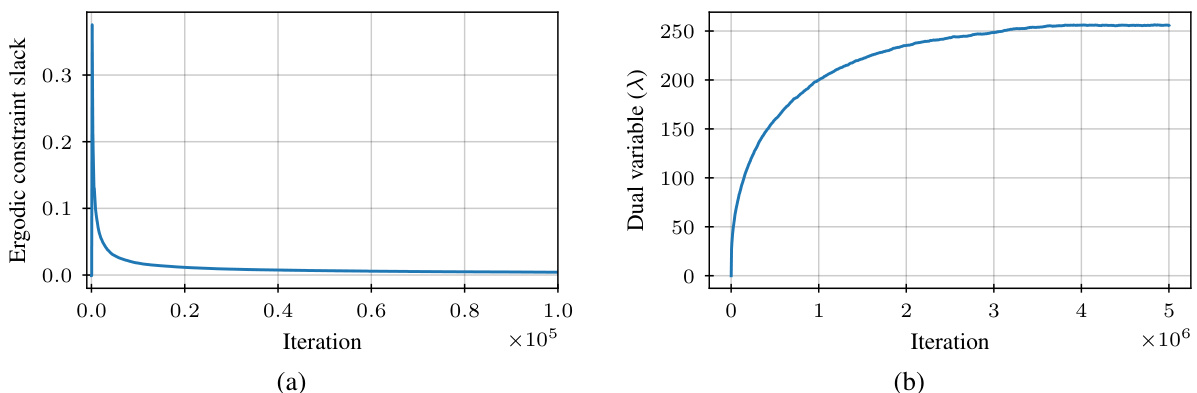
This figure shows the results of using the primal-dual Langevin Monte Carlo (PD-LMC) algorithm to sample from a one-dimensional truncated Gaussian distribution. Panel (a) displays the ergodic average of the constraint function (slack), which measures how well the samples satisfy the constraint. Panel (b) shows the evolution of the dual variable λ, which is used to enforce the constraint. The figure demonstrates that the PD-LMC algorithm is able to efficiently sample from the constrained distribution.

This figure shows the results of a fair Bayesian logistic regression model applied to the Adult dataset. Panel (a) displays the distribution of the probability of predicting an income greater than $50k for males and females, both under an unconstrained model and a constrained model that enforces statistical parity. Panel (b) illustrates the evolution of the dual variables (Lagrange multipliers) during the optimization process, one for the female constraint and one for the male constraint.

This figure shows the effect of the mini-batch size (Nb) on the performance of the Primal-Dual Langevin Monte Carlo (PD-LMC) algorithm in a fair Bayesian classification task. The x-axis represents the prevalence of individuals predicted to earn over $50k, and the y-axis represents the different mini-batch sizes tested, along with the computation time for each size. Each row shows violin plots of the prevalence distribution for a specific mini-batch size. The black vertical line represents the mean of the distribution for each mini-batch size. This visual helps to assess the impact of varying mini-batch sizes on the algorithm’s convergence and accuracy in achieving fairness.

This figure shows the results of a counterfactual sampling experiment using a fair Bayesian logistic regression model. Panel (a) displays the mean coefficients for several variables in the model under both unconstrained and constrained conditions. Panel (b) illustrates the effect of varying the tolerance (δ) parameter on the prevalence of positive outputs, with separate distributions shown for males and females. The figure demonstrates how the model’s predictions and the effects of fairness constraints can change based on the tolerance level.
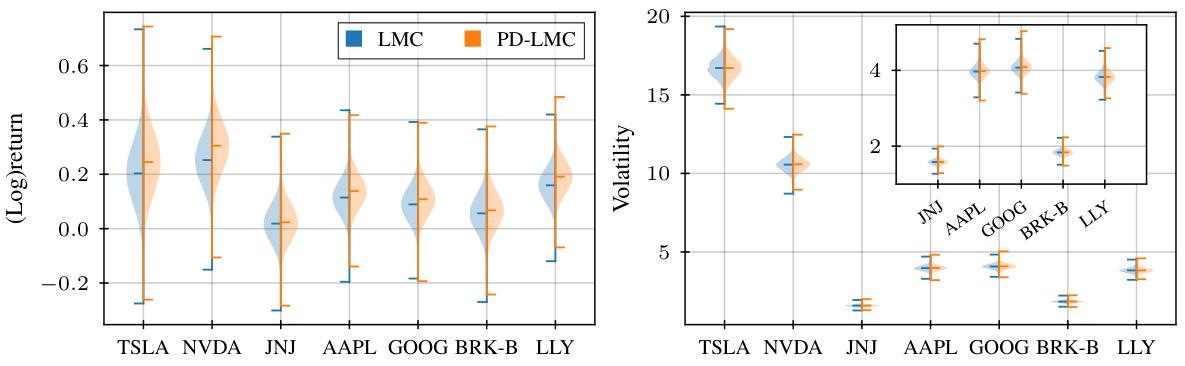
This figure compares the mean and variance of stock returns obtained from the original Bayesian model (LMC) and the constrained model (PD-LMC) where a 20% average return increase was enforced on each stock. The violin plots visually represent the distribution of each parameter across the different stocks, highlighting differences between the unconstrained and constrained models. The plots show how the constraints influence not only the means, but also the volatilities of the stock returns.

This figure shows the results of a counterfactual sampling experiment on a stock market model. Panel (a) displays the ergodic average of the constraint functions (slacks) over iterations of the PD-LMC algorithm. It shows how well the algorithm satisfies the constraints (20% increase in average return). Panel (b) shows the evolution of the dual variables (λ) which are associated with the constraints. These variables reflect the importance of each constraint in the optimization process. The plot reveals the convergence behavior of the dual variables, showing that the algorithm is successfully adjusting the dual variables to satisfy the constraints.

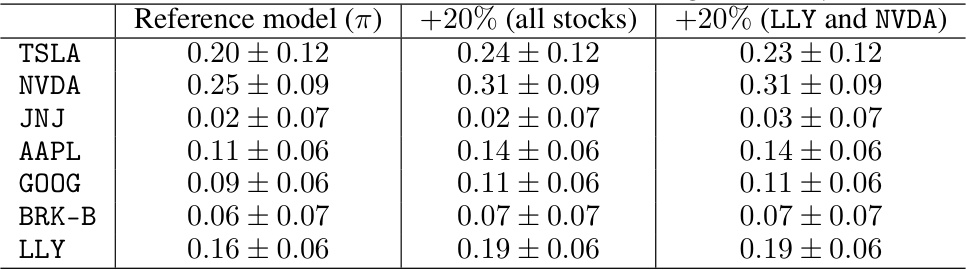
This figure compares the distributions of mean (log-)returns (p) and volatilities (diag(∑)) for seven stocks (TSLA, NVDA, JNJ, AAPL, GOOG, BRK-B, and LLY) under two scenarios: 1. All stocks: A 20% average return increase is imposed on all seven stocks using constrained sampling. 2. NVDA, LLY: A 20% average return increase is imposed only on NVDA and LLY stocks, while other stocks’ returns were not constrained. Violin plots show the distributions of these parameters, highlighting the differences between the two scenarios. The results suggest that constraining only NVDA and LLY’s returns has a substantial impact on the entire market’s distribution of returns and volatilities.
More on tables

This table compares the mean and variance estimates obtained from different sampling methods for two examples: 1D truncated Gaussian and 2D truncated Gaussian. The ‘True mean’ column shows the actual mean of the target distribution. The ‘Proj. LMC’, ‘Mirror LMC’, and ‘PD-LMC’ columns show the estimated means obtained from the Projected Langevin Monte Carlo, Mirror Langevin Monte Carlo, and Primal-Dual Langevin Monte Carlo methods, respectively. The difference highlights the accuracy of the proposed PD-LMC method compared to other methods in estimating the mean of truncated Gaussian distributions.
This table compares the mean and variance estimates obtained from different sampling methods (PD-LMC, Projected LMC, Mirror LMC) for both 1D and 2D truncated Gaussian distributions. It highlights the accuracy of each method in estimating the true mean and variance of the distributions.
Full paper#