TL;DR#
Many machine learning applications involve solving distributed minimax optimization problems. Traditional methods, however, often struggle with convergence due to inconsistencies in locally computed adaptive stepsizes. This inconsistency arises from the lack of coordination in stepsizes among different nodes in the distributed system, leading to non-convergence or significantly slower convergence speeds.
The paper proposes D-AdaST, a novel Distributed Adaptive minimax method with Stepsize Tracking. D-AdaST employs an innovative stepsize tracking protocol involving the transmission of only two extra scalar variables. This protocol maintains stepsize consistency, addressing the challenges of existing methods. Theoretically, the authors prove that D-AdaST achieves a near-optimal convergence rate under specific assumptions, matching the performance of centralized methods. Extensive experiments demonstrate the effectiveness and superiority of D-AdaST over existing methods in various real-world applications.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the critical challenge of achieving near-optimal convergence in distributed minimax optimization, a problem prevalent in many machine learning applications. It presents a novel solution, D-AdaST, overcoming limitations of existing methods by ensuring stepsize consistency and time-scale separation. This opens new avenues for developing more efficient and robust distributed algorithms for various minimax problems in areas like GAN training and robust optimization.
Visual Insights#
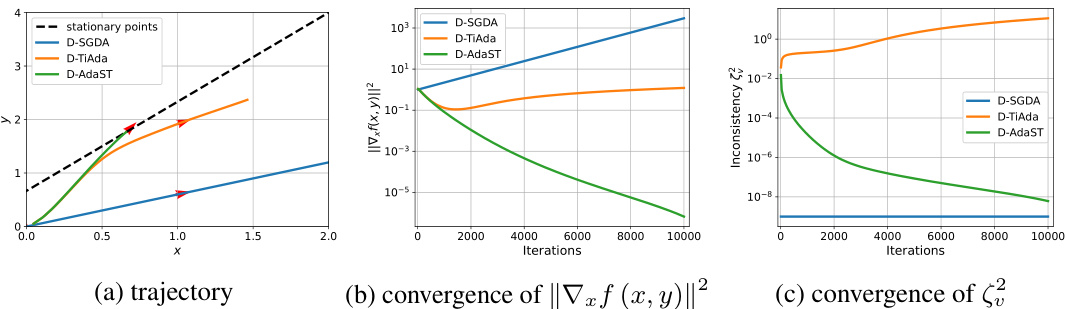
🔼 This figure compares three distributed adaptive minimax optimization algorithms: D-SGDA, D-TiAda, and D-AdaST. Subfigure (a) shows the trajectories of primal and dual variables for each algorithm on a simple NC-SC quadratic objective function with only 2 nodes. The black dashed line indicates the stationary points of the objective function. Subfigure (b) plots the convergence of ||∇x f (xk, Yk)||², which measures the norm of the gradient of the objective function with respect to the primal variable x. Subfigure (c) displays the convergence of the stepsize inconsistency (ξ2). This inconsistency is a key issue with vanilla distributed adaptive methods, and this figure highlights how D-AdaST effectively addresses it.
read the caption
Figure 1: Comparison among D-SGDA, D-TiAda and D-AdaST for NC-SC quadratic objective function (6) with n = 2 nodes and x = y. In (a), it shows the trajectories of primal and dual variables of the algorithms, the points on the black dash line are stationary points of f. In (b), it shows the convergence of ||∇x f (xk, Yk)||² over the iterations. In (c), it shows the convergence of the inconsistency of stepsizes, ξ2 defined in (8), over the iterations. Notably, ξ2 fails to converge for D-TiAda and ξ2 = 0 for non-adaptive D-SGDA.
In-depth insights#
Adaptive Minimax#
Adaptive minimax optimization presents a powerful paradigm for solving problems involving competing objectives, particularly in machine learning scenarios. Adaptivity, by adjusting parameters (like step sizes) based on the data, addresses the challenges of non-convexity and strong concavity. Minimax formulations elegantly capture the adversarial nature of many machine learning tasks, such as GAN training. The combination leads to algorithms that are both efficient and robust. However, challenges remain, especially in decentralized settings, as local adaptivity can lead to inconsistencies between nodes. Addressing such issues through techniques like stepsize tracking is crucial for effective distributed adaptive minimax algorithms. The theoretical analysis of convergence rates, often focusing on near-optimal bounds, is vital for understanding performance. Practical applications span various fields, including robust optimization and GANs, highlighting the importance of further research into efficient and robust adaptive minimax methods for real-world applications.
D-AdaST Algorithm#
The D-AdaST algorithm, a distributed adaptive minimax optimization method, tackles the convergence issues arising from inconsistent local stepsizes in decentralized settings. Its core innovation lies in a stepsize tracking protocol, which ensures consistency among all nodes by transmitting only two scalar variables. This protocol is crucial because it eliminates the steady-state error often present in vanilla distributed adaptive methods. D-AdaST achieves a near-optimal convergence rate for nonconvex-strongly-concave minimax problems without needing prior knowledge of problem-dependent parameters, making it truly parameter-agnostic and highly practical. Theoretical analysis rigorously establishes its near-optimal performance, characterizing the transient times needed to ensure timescale separation of stepsizes and quasi-independence of the network. Extensive experiments further validate the theoretical findings, demonstrating significant performance gains over existing methods in diverse scenarios, including robust neural network training and Wasserstein GAN optimization.
Convergence Analysis#
A rigorous convergence analysis is crucial for validating the effectiveness of any optimization algorithm. In the context of distributed adaptive minimax optimization, this analysis becomes particularly challenging due to the inherent complexities of decentralized systems and the adaptive nature of the stepsizes. A comprehensive convergence analysis should consider various factors such as the non-convexity of the objective function, strong concavity of the minimax problem’s dual variable, the network topology of the distributed system, and the consistency of adaptive stepsizes across all nodes. It’s imperative to establish theoretical bounds on the convergence rate under these conditions and to prove that the algorithm converges to a stationary point or an e-stationary point. Furthermore, a good analysis should address the time-scale separation of stepsizes and its role in achieving convergence, as this is often vital for successful minimax optimization. Finally, theoretical results should be compared with the practical performance of the algorithm to assess its applicability and efficiency. This thorough analysis helps to determine the limitations and potential improvements of the algorithm.
Experimental Results#
The Experimental Results section of a research paper is crucial for validating the claims made and demonstrating the effectiveness of proposed methods. A strong Experimental Results section will present findings in a clear, concise manner, using appropriate visualizations (graphs, tables, etc.) to illustrate key trends. Robustness checks, such as varying parameters and testing on multiple datasets or scenarios, should be included to demonstrate the generalizability of the results beyond specific settings. Quantitative metrics that are relevant to the research problem should be carefully chosen and presented. Furthermore, the discussion should acknowledge limitations of the experimental setup and potential confounding factors. A thoughtful analysis that compares results against existing state-of-the-art approaches or establishes baselines is also essential. Statistical significance should be properly addressed, potentially incorporating error bars or p-values to highlight the confidence in the obtained results. A well-structured section will aid in the reproducibility of the research and increase the overall credibility and impact of the paper.
Future Directions#
Future research could explore several promising avenues. Extending D-AdaST to handle more complex network topologies beyond the well-connected and exponential graphs considered would enhance its applicability in decentralized settings. Investigating its performance under asynchronous communication and heterogeneous computational resources is crucial for realistic deployments. Further theoretical work could focus on weakening the strong concavity assumption, extending the analysis to a broader class of nonconvex-nonconcave problems. Finally, empirical studies on larger scale applications, such as training massive deep neural networks or solving challenging minimax games, would demonstrate its practical effectiveness. Exploring the interaction between adaptive stepsizes and other regularization techniques, like momentum or variance reduction, might lead to further convergence improvements. The potential of developing novel stepsize tracking protocols that are more communication-efficient or robust to noise would significantly impact the scalability and efficiency of distributed minimax optimization.
More visual insights#
More on figures
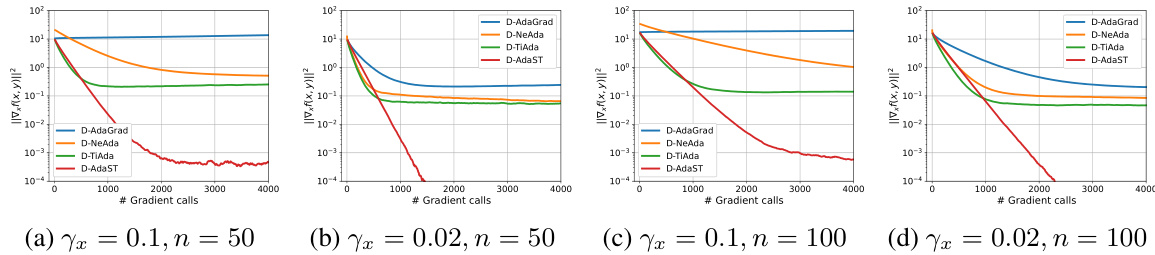
🔼 The figure compares the performance of four distributed adaptive minimax optimization algorithms (D-AdaGrad, D-NeAda, D-TiAda, and D-AdaST) on solving non-convex strongly concave quadratic objective functions across different network sizes (n=50 and n=100) and initial stepsizes. The plots illustrate the convergence of the algorithms, measured by the squared norm of the gradient of the primal variable (||∇xf(x,y)||²), over the number of gradient calls. The results demonstrate that D-AdaST consistently outperforms other algorithms across various settings, highlighting its effectiveness and robustness in distributed environments. The plots demonstrate the impact of network size and initial stepsizes on algorithm performance.
read the caption
Figure 2: Performance comparison of algorithms on quadratic functions over exponential graphs with node counts n = {50, 100} and different initial stepsizes (yy = 0.1).
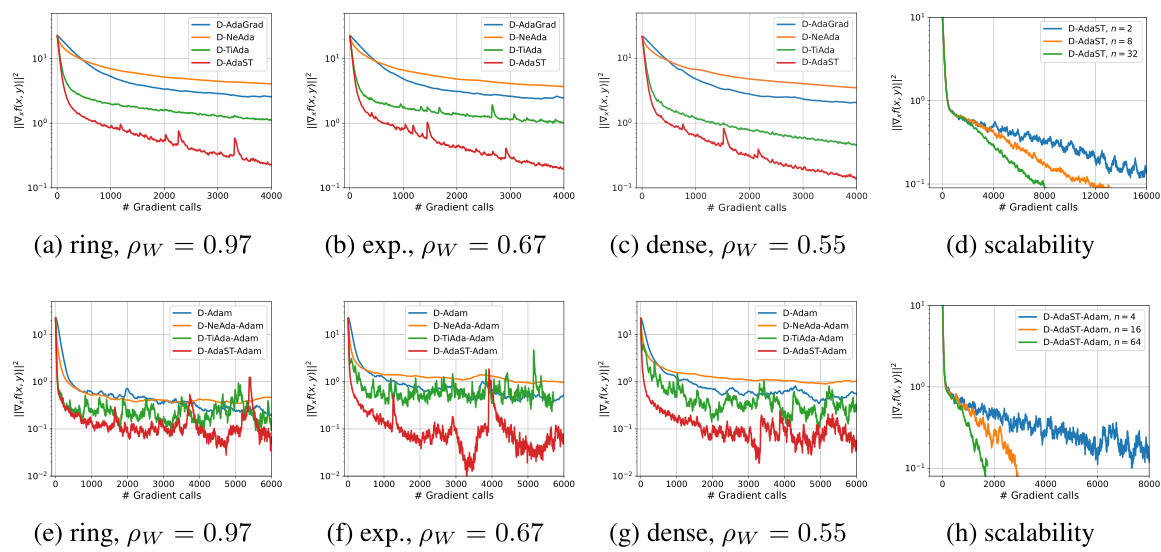
🔼 This figure compares the performance of three distributed minimax optimization algorithms (D-SGDA, D-TiAda, and D-AdaST) on a simple nonconvex-strongly-concave quadratic objective function. It illustrates the trajectories of primal and dual variables, the convergence of the gradient norm, and importantly, the convergence of the inconsistency in stepsizes. The results highlight that D-AdaST is the only algorithm that converges to a stationary point and resolves the issue of inconsistent stepsizes.
read the caption
Figure 1: Comparison among D-SGDA, D-TiAda and D-AdaST for NC-SC quadratic objective function (6) with n = 2 nodes and x = y. In (a), it shows the trajectories of primal and dual variables of the algorithms, the points on the black dash line are stationary points of f. In (b), it shows the convergence of ||∇x f (xk, Yk)||² over the iterations. In (c), it shows the convergence of the inconsistency of stepsizes, 2 defined in (8), over the iterations. Notably, 2 fails to converge for D-TiAda and 2 = 0 for non-adaptive D-SGDA.
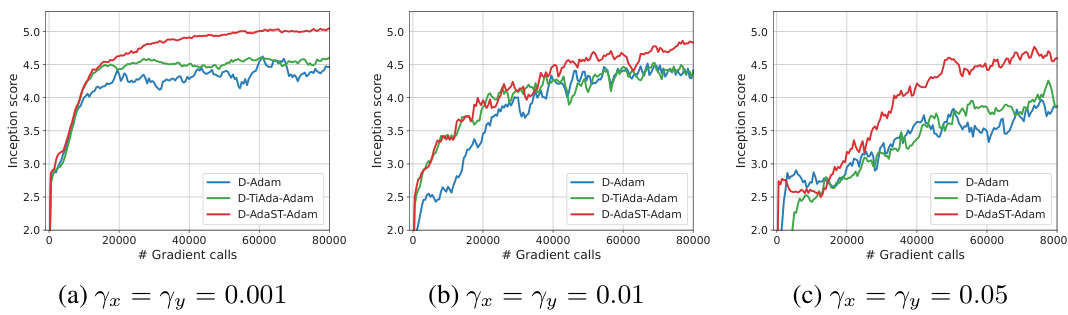
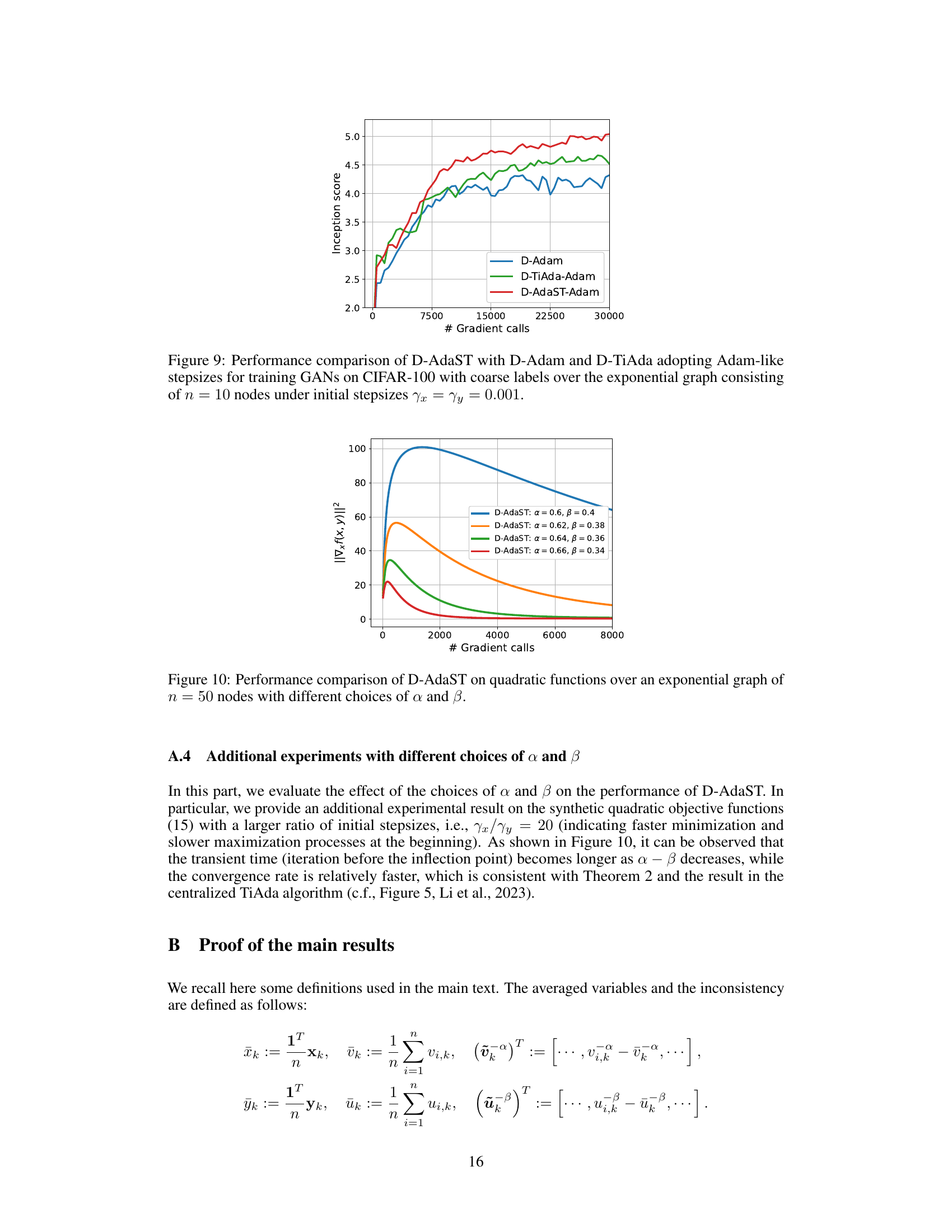
🔼 The figure compares the performance of three different algorithms (D-Adam, D-TiAda-Adam, and D-AdaST-Adam) on training GANs using the CIFAR-10 dataset. The experiment is performed on an exponential graph with 10 nodes. The x-axis represents the number of gradient calls, and the y-axis represents the inception score, a measure of the quality of the generated images. Three subplots show results for different initial stepsizes (γx = γy = 0.001, γx = γy = 0.01, γx = γy = 0.05). The results demonstrate that D-AdaST-Adam consistently achieves a higher inception score, indicating superior performance in generating high-quality images.
read the caption
Figure 4: Training GANs on CIFAR-10 dataset over exponential graphs with n = 10 nodes.
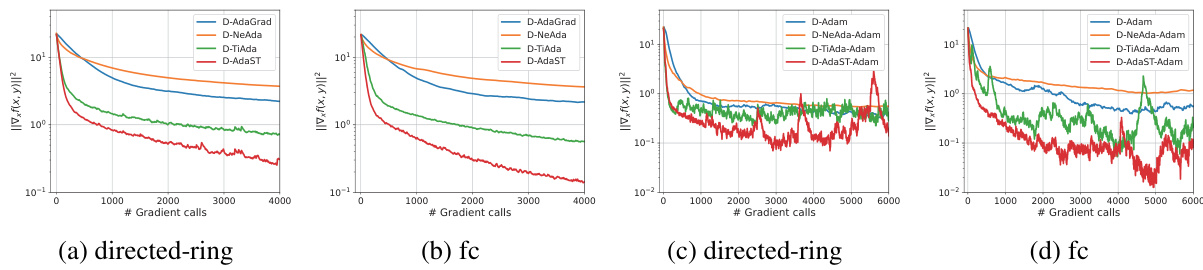
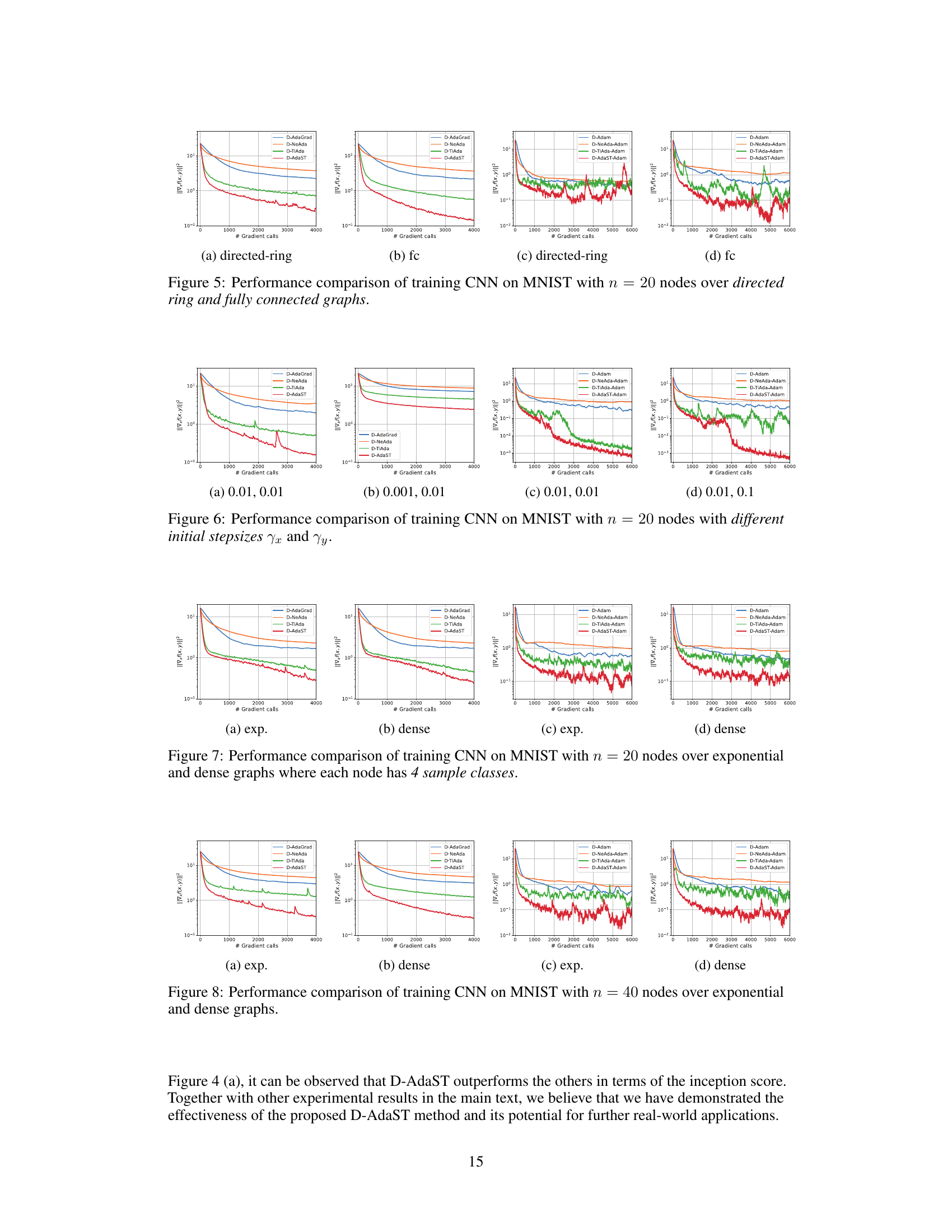
🔼 The figure compares the performance of four different distributed adaptive minimax optimization algorithms (D-AdaGrad, D-NeAda, D-TiAda, and D-AdaST) on training a Convolutional Neural Network (CNN) for image classification using the MNIST dataset. The algorithms are evaluated across two different graph topologies: directed ring and fully connected. The plot shows the convergence of the algorithms measured by the squared norm of the gradient of the loss function, (||\nabla_x f(x, y)|^2), against the number of gradient calls. The results demonstrate how D-AdaST outperforms other algorithms, especially in a dense graph topology, indicating the proposed algorithm’s robustness and effectiveness.
read the caption
Figure 5: Performance comparison of training CNN on MNIST with n = 20 nodes over directed ring and fully connected graphs.
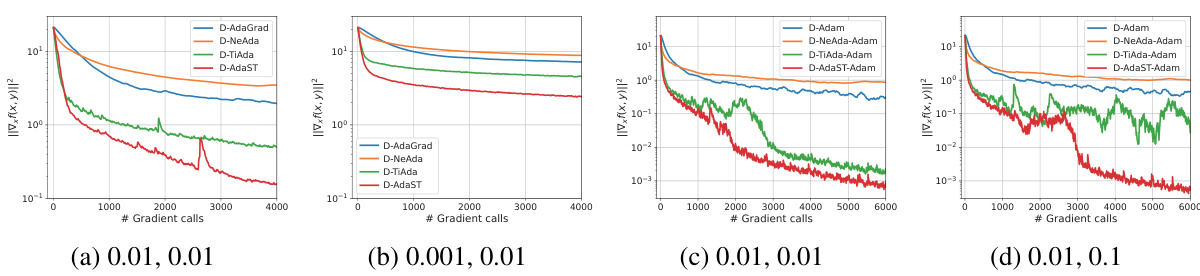
🔼 The figure compares the performance of D-AdaGrad, D-NeAda, D-TiAda, and D-AdaST algorithms on quadratic functions. It shows the convergence of ||∇xf(x, y)||² (the squared norm of the gradient of f with respect to x) over the number of gradient calls. The comparison is made for two different network sizes (n=50 and n=100 nodes) and two different initial stepsize settings (x=0.1 and x=0.02, with y=0.1 in both cases). The plots illustrate how D-AdaST consistently achieves faster convergence compared to other algorithms across all settings.
read the caption
Figure 2: Performance comparison of algorithms on quadratic functions over exponential graphs with node counts n = {50, 100} and different initial stepsizes (yy = 0.1).
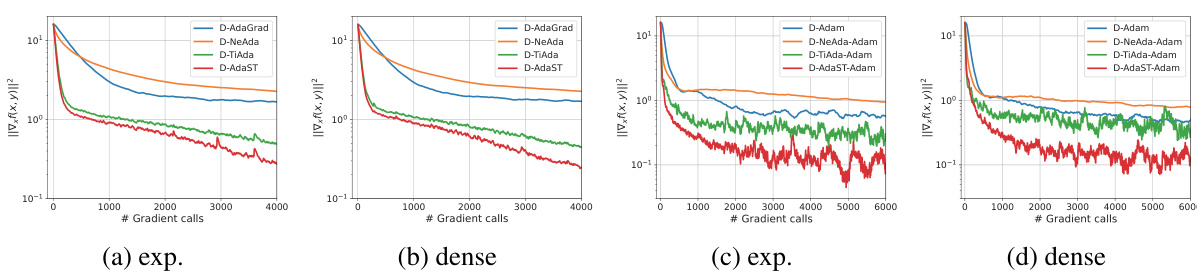
🔼 This figure compares the performance of four distributed adaptive minimax optimization algorithms (D-AdaGrad, D-NeAda, D-TiAda, and D-AdaST) on a quadratic objective function using two different graph topologies (exponential and dense graphs) and two different numbers of nodes (50 and 100). The algorithms differ in how they handle step sizes: D-AdaGrad is a basic adaptive method; D-NeAda is a nested adaptive method; D-TiAda is a single-loop adaptive method with time-scale separation; and D-AdaST is a newly proposed method that includes a stepsize tracking mechanism to improve consistency of step sizes across nodes. The plots show the convergence of the gradient norm ||∇xf(x,y)||² as a function of the number of gradient calls. The results demonstrate that D-AdaST achieves faster convergence compared to the other algorithms, especially when the initial step size is favorable. This highlights the effectiveness of the step size tracking mechanism in D-AdaST for ensuring the convergence of distributed adaptive methods.
read the caption
Figure 2: Performance comparison of algorithms on quadratic functions over exponential graphs with node counts n = {50, 100} and different initial stepsizes (yy = 0.1).
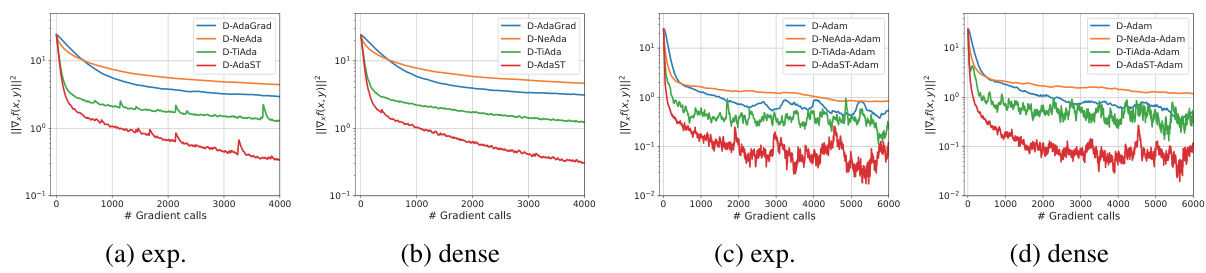
🔼 This figure compares the performance of four different distributed adaptive minimax optimization algorithms (D-AdaGrad, D-NeAda, D-TiAda, and D-AdaST) on two different graph topologies (exponential and dense graphs) with varying node counts (n = 50 and n = 100). The algorithms are tested using two sets of initial stepsizes (x=0.1, y=0.1 and x=0.02, y=0.1) to find an e-stationary point of a nonconvex-strongly concave quadratic function. The plots show the convergence of ||∇x f(x,y)||² over gradient calls. The results demonstrate that D-AdaST consistently outperforms other algorithms across various settings.
read the caption
Figure 2: Performance comparison of algorithms on quadratic functions over exponential graphs with node counts n = {50, 100} and different initial stepsizes (yy = 0.1).
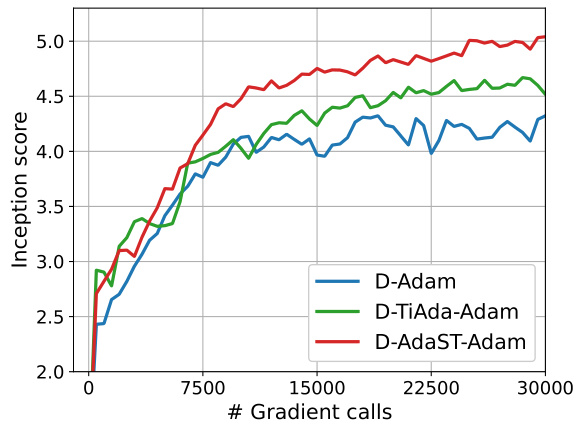
🔼 This figure compares the performance of three distributed adaptive minimax optimization algorithms, namely D-Adam, D-TiAda-Adam, and D-AdaST-Adam, on the task of training Generative Adversarial Networks (GANs) using the CIFAR-10 dataset. The x-axis represents the number of gradient calls, and the y-axis represents the inception score, a metric used to evaluate the quality of generated images. The experiment was conducted on an exponential graph with 10 nodes. The figure demonstrates that D-AdaST-Adam achieves a higher inception score compared to the other two algorithms, indicating its superior performance in this task.
read the caption
Figure 4: Training GANs on CIFAR-10 dataset over exponential graphs with n = 10 nodes.
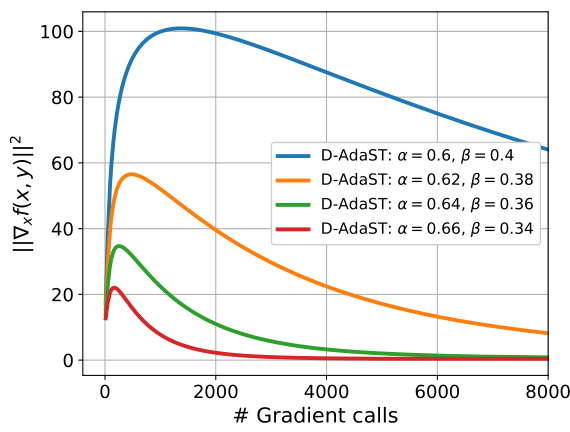
🔼 This figure shows the performance of the D-AdaST algorithm on quadratic functions with different choices of α and β parameters over an exponential graph with 50 nodes. It illustrates how the convergence rate is affected by the selection of α and β. The plot shows that smaller values of α - β lead to faster initial convergence but possibly a higher steady-state error.
read the caption
Figure 10: Performance comparison of D-AdaST on quadratic functions over an exponential graph of n = 50 nodes with different choices of α and β.
Full paper#