TL;DR#
Many existing distributed machine learning algorithms struggle with the inconsistent processing speeds of individual worker nodes and the time spent communicating results between them, significantly impacting efficiency. These methods often fail to account for these variations, which can lead to suboptimal performance. Previous asynchronous SGD methods also lacked robustness in the face of such inconsistencies.
The research introduces Shadowheart SGD, a novel asynchronous SGD algorithm designed to address these issues. It leverages unbiased compression techniques to improve communication efficiency and incorporates a strategy that dynamically adjusts computations based on node processing times. This results in optimal time complexity across diverse worker node and communication network characteristics. The new approach outperforms existing algorithms in a wide range of settings and includes extensions for handling bidirectional communication.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in distributed machine learning due to its optimal time complexity solution for asynchronous SGD. It tackles the significant challenges of communication and computation heterogeneity, offering a robust and efficient algorithm. This work advances the field, prompting further research into adaptive algorithms and potentially impacting the development of real-world distributed systems.
Visual Insights#
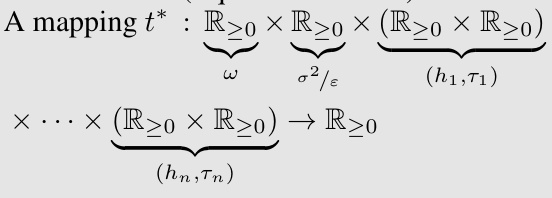
🔼 The plots show the results of logistic regression experiments on the MNIST dataset, comparing Shadowheart SGD’s performance with various baselines (QSGD, Asynchronous SGD, Minibatch SGD, SGDone). Three different communication speed regimes are considered: high, medium, and low. The figure illustrates Shadowheart SGD’s robustness to varying communication speeds, consistently achieving strong performance across all regimes.
read the caption
Figure 1: Experiments with logistic regression.

🔼 The table compares the time complexities of several centralized distributed algorithms for solving nonconvex smooth optimization problems. It considers scenarios with varying computation and communication times across different workers, and employs a compression technique to reduce communication overhead. The algorithms compared are Minibatch SGD, QSGD, Rennala SGD, Asynchronous SGD, and Shadowheart SGD. The table highlights the time complexities under different regimes (equal performance, slow last worker, etc.) and provides a numerical comparison demonstrating that Shadowheart SGD outperforms previous methods in various scenarios.
read the caption
Table 1: Time Complexities of Centralized Distributed Algorithms. Assume that it takes at most hi seconds to worker i to calculate a stochastic gradient and † seconds to send one coordinate/float to server. Abbreviations: L = smoothness constant, ε = error tolerance, ∆ = f(xº) – f*, n = # of workers, d = dimension of the problem. We take the RandK compressor with K = 1 (Def. D.1) (as an example) in QSGD and Shadowheart SGD. Due to Property 6.2, the choice K = 1 is optimal for Shadowheart SGD up to a constant factor.
In-depth insights#
Shadowheart’s Core#
Shadowheart’s Core likely refers to the algorithm’s central mechanism, likely a novel variant of stochastic gradient descent (SGD). The paper likely details how Shadowheart optimizes asynchronous distributed SGD, addressing computational and communication heterogeneities across multiple worker nodes. Key innovations probably involve a sophisticated gradient compression technique (reducing communication overhead) and a strategic worker scheduling strategy (balancing computation speeds). Optimal time complexity is a significant claim, suggesting the algorithm achieves a superior balance of accuracy and efficiency compared to existing approaches. The core likely incorporates mechanisms to handle arbitrary delays and worker failures, contributing to the claimed robustness. A theoretical analysis, possibly through mathematical proofs, should underpin the claims of optimality. Finally, Shadowheart’s core likely includes adaptive elements, adjusting its behavior dynamically based on observed system conditions.
Async SGD Edge#
An “Async SGD Edge” heading suggests a research focus on improving asynchronous stochastic gradient descent (SGD) algorithms, specifically within the context of edge computing. This likely involves tackling challenges inherent in distributed systems at the network’s edge, such as high latency, limited bandwidth, and heterogeneous device capabilities. The approach might involve novel techniques for gradient compression, communication-efficient aggregation, or fault tolerance to ensure convergence despite unreliable network connections and intermittent device availability. The “Edge” component implies a departure from centralized server-based training, pushing computation and learning closer to the data sources. This could offer benefits such as reduced latency, improved privacy, and increased efficiency for applications like real-time processing or Internet-of-Things (IoT) deployments. The work could also explore optimizing for specific edge hardware or addressing constraints related to energy consumption and storage capacity. A key aspect of the research would be quantifying the trade-offs between communication efficiency, computational overhead, and the achieved model accuracy on edge devices.
Optimal Complexity#
The concept of ‘Optimal Complexity’ in a research paper is multifaceted. It usually signifies a theoretical analysis demonstrating that an algorithm achieves the best possible runtime or resource usage under specified conditions, often concerning computational time, memory, or communication. This optimality is typically proven relative to a defined class of algorithms and a specific problem setting, demonstrating a fundamental limit. Establishing optimal complexity is a significant contribution, showcasing the algorithm’s efficiency and theoretical robustness. The proof often involves intricate mathematical arguments and lower bound derivations to rule out the existence of superior algorithms. Practical implications involve efficiency and scalability. An algorithm with optimal complexity can be particularly crucial for large-scale problems where resource constraints are paramount. However, optimality rarely implies practical dominance in all cases. Factors such as constant factors in the complexity analysis or the algorithm’s sensitivity to specific problem characteristics can affect real-world performance. Therefore, while an ‘Optimal Complexity’ result is theoretically significant, it must be considered alongside other practical factors for comprehensive evaluation.
Heterogeneity Test#
A hypothetical ‘Heterogeneity Test’ section in a research paper would likely explore the robustness of a proposed algorithm (e.g., a novel distributed SGD method) across diverse computational and communication environments. This would involve systematically varying parameters such as worker compute speeds, network latency, and bandwidth to assess performance consistency. The results might show that the algorithm maintains optimal time complexity despite significant worker heterogeneity, showcasing its effectiveness across realistic, non-uniform settings. A key finding could demonstrate resilience to stragglers (slow workers) or the impact of network fluctuations, proving practical advantage in decentralized machine learning. Analyzing this would require careful consideration of how heterogeneity affects convergence rate, accuracy, and overall efficiency. This section’s importance is in verifying the practical applicability of theoretical findings, building confidence in the algorithm’s real-world deployment potential and highlighting its advantages over existing approaches which might struggle with such inconsistencies.
Future Extensions#
Future extensions of this research could explore several promising avenues. Addressing statistical heterogeneity among workers, currently assumed uniform, is crucial for broader applicability. This would involve developing robust algorithms that can handle variations in data distributions across different nodes. Another key area is incorporating more sophisticated compression techniques, beyond the unbiased compression methods used. This could potentially lead to further improvements in communication efficiency and overall runtime. Investigating alternative aggregation strategies beyond simple averaging could also be beneficial. The study’s focus on device heterogeneity makes it particularly relevant to federated learning; future work could thus examine applications in this area, along with comparisons to existing federated optimization algorithms. Finally, a thorough investigation of the optimal step size selection and its interaction with different problem characteristics and hardware configurations would further enhance the algorithm’s practical performance and theoretical understanding.
More visual insights#
More on figures

🔼 This figure compares the time complexities of different centralized distributed algorithms (Minibatch SGD, QSGD, Rennala SGD, Asynchronous SGD, and Shadowheart SGD) across three communication speed regimes: high, low, and medium. The x-axis represents the time in seconds, and the y-axis represents the difference between the current function value and optimal function value. Different colors represent different algorithms. The figure illustrates the performance of Shadowheart SGD relative to existing methods under varying communication conditions.
read the caption
Figure 1: Time complexities of centralized distributed algorithms in different regimes. (a) high communication speed; (b) low communication speed; (c) medium communication speed.
🔼 This figure presents the results of experiments on logistic regression using the MNIST dataset, comparing Shadowheart SGD with QSGD, Asynchronous SGD, Minibatch SGD, and SGDone. Three communication speed setups are shown: high, medium, and low. The plots illustrate the convergence rate of each algorithm measured in terms of f(xt) - f(x*) against time in seconds. Different step sizes were used for each algorithm to fine-tune performance and the parameter σ²/ɛ was tuned for Shadowheart SGD. The high communication speed setup shows all the distributed algorithms performing similarly, while the lower speed communications demonstrate how Shadowheart SGD is robust across different scenarios.
read the caption
Figure 1: Experiments with logistic regression.
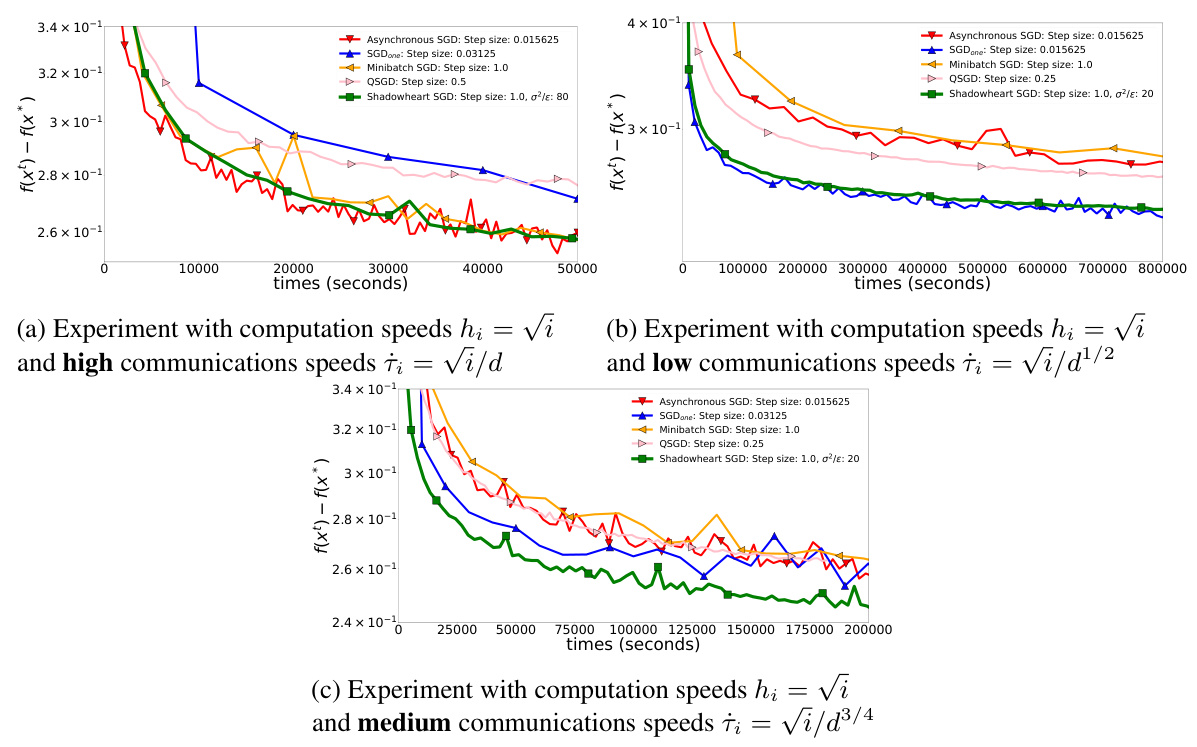
🔼 This figure compares the performance of various algorithms on synthetic quadratic optimization tasks with multiplicative noise. The x-axis represents the time in seconds, and the y-axis represents the objective function value. The plots show that as noise increases (comparing (a) and (b)), the performance of SGDone degrades significantly relative to Shadowheart SGD, while other methods also show some performance degradation. Shadowheart SGD demonstrates superior robustness to increasing noise levels.
read the caption
Figure 2: SGDone starts to slow down relative to Shadowheart SGD and other methods when we increase the noise.
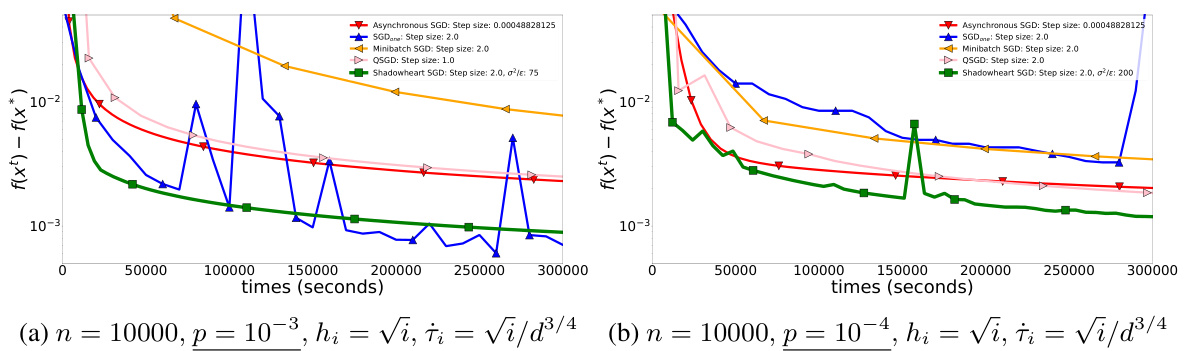
🔼 This figure compares the performance of Shadowheart SGD against other methods (Asynchronous SGD, SGDone, Minibatch SGD, and QSGD) on synthetic quadratic optimization tasks with multiplicative noise. The x-axis represents the time in seconds, and the y-axis represents the difference between the function value at the current iterate and the optimal function value (f(xt) - f(x*)). The plots show that as noise increases (from p = 10⁻³ in (a) to p = 10⁻⁴ in (b)), SGDone’s performance deteriorates significantly, whereas Shadowheart SGD maintains its relative advantage over other methods.
read the caption
Figure 2: SGDone starts to slow down relative to Shadowheart SGD and other methods when we increase the noise.
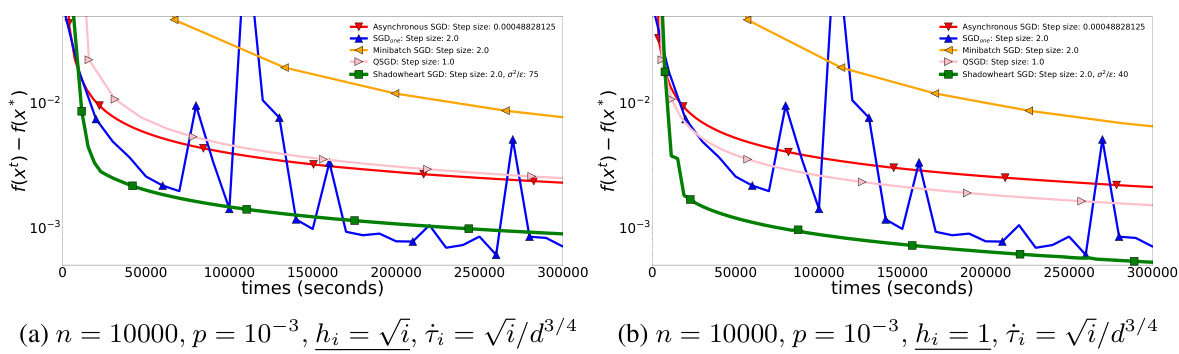
🔼 This figure compares the performance of Shadowheart SGD against other methods (Asynchronous SGD, SGDone, Minibatch SGD, QSGD) under different computation times. In (a), computation times are √i, showcasing Shadowheart SGD’s robustness and improved convergence compared to others, particularly as the communication time increases. Part (b) uses a constant computation time of 1 for all workers. The difference highlights how Shadowheart SGD’s performance benefits from reducing the variance in computation times.
read the caption
Figure 4: Shadowheart SGD improves when we decrease the computation times from √i to 1.

🔼 This figure presents the results of experiments comparing the convergence speed of various algorithms for different numbers of workers (n). The x-axis represents the time in seconds, and the y-axis represents the value of ||∇f(x)||². The figure showcases the performance of Asynchronous SGD, SGDone, Minibatch SGD, QSGD, and Shadowheart SGD across three different communication speed settings (β = 1/2, 3/4, 1), which are indicated in subplots (a), (b), and (c) respectively. Each subplot corresponds to a different number of workers: (a) n = 10, (b) n = 10², and (c) n = 10³. The goal is to show how the convergence of Shadowheart SGD compares with the other algorithms under various worker and communication conditions.
read the caption
Figure 5: hᵢ ~ U(0.1, 1), tᵢ = √i/dβ, β ∈ {1/2, 3/4, 1}

🔼 This figure displays the convergence of different SGD methods (Shadowheart SGD, Asynchronous SGD, SGDone, Minibatch SGD, and QSGD) when the computation time for each worker changes. The y-axis shows the convergence speed, measured as ||∇f(xk)||², while the x-axis represents the time. The three subfigures correspond to different noise levels (σ²/ε = 1, 10, 102). Shadowheart SGD is shown to improve in all noise levels when computation time decreases from √i to 1.
read the caption
Figure 4: Shadowheart SGD improves when we decrease the computation times from √i to 1.
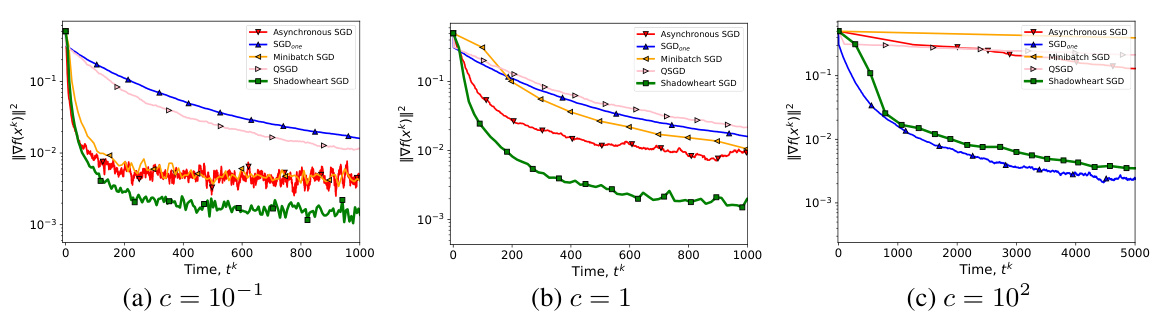
🔼 This figure shows the convergence speed of different algorithms under additive noise, where computation and communication times are sampled from the uniform distribution U(0.1, 1). The communication times are scaled by a factor c, which represents different communication speed regimes: c = 10⁻¹, c = 1, and c = 10². Shadowheart SGD demonstrates robustness and high convergence speed across different regimes, particularly excelling in high and medium-speed communication. SGDone, while competitive in scenarios with expensive communications (c = 10²), is outperformed by Shadowheart SGD as communication speed improves.
read the caption
Figure 7: h ~ U(0.1, 1), † ~ c · U(0.1, 1)

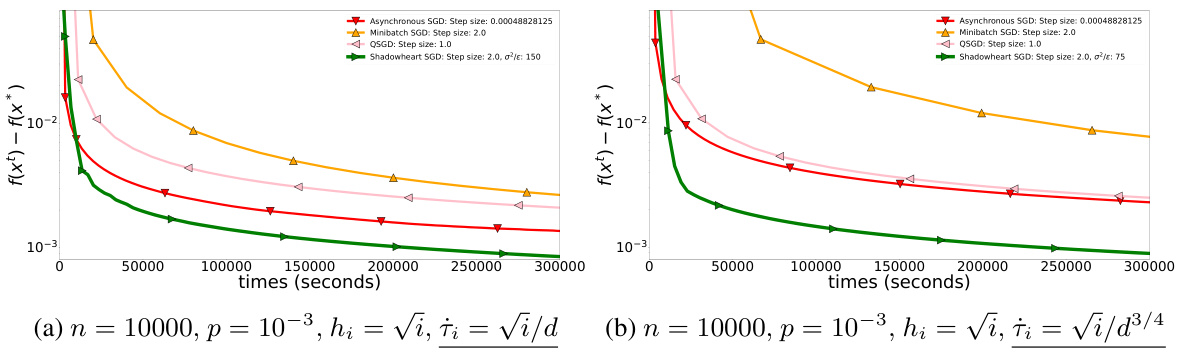
🔼 This figure compares the performance of Shadowheart SGD against Asynchronous SGD, Minibatch SGD, and QSGD across three different communication time regimes. The x-axis represents time in seconds, and the y-axis represents the convergence metric ||∇f(x)||². The plots show that Shadowheart SGD consistently outperforms the other methods, particularly in high-communication cost scenarios, showcasing its robustness to communication delays.
read the caption
Figure 3: The non-compressed methods Asynchronous SGD and Minibatch SGD slow down relative to Shadowheart SGD when we increase the communication times.
Full paper#



















