Understanding Representation of Deep Equilibrium Models from Neural Collapse Perspective

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap between implicit and explicit neural networks, a significant challenge in deep learning. By applying the Neural Collapse framework to the Deep Equilibrium Model, it offers new theoretical insights and practical advantages for handling imbalanced datasets, a common issue in real-world applications. The findings advance our understanding of implicit models, suggesting new research avenues in model representation and robustness.

Visual Insights

#

This figure illustrates the feature extraction process for both explicit neural networks and DEQs. An image encoder processes the input image (x) to produce initial features (Hº). These features then pass through either a series of explicit layers (in the explicit neural network branch) or a deep equilibrium model (DEQ) solver to produce refined features (H for explicit networks, z* for DEQ). Finally, a classifier (W) maps these refined features to logits (predictions). For consistent comparison, the image encoder and the initial feature output (Hº) are standardized across both approaches.

This table compares the accuracy of Explicit Neural Networks (Explicit NN) and Deep Equilibrium Models (DEQ) on the Cifar-10 and Cifar-100 datasets under balanced conditions. The results show that DEQ achieves slightly higher accuracy than Explicit NN on both datasets, though the differences are relatively small.

In-depth insights

#

DEQ’s NC Behavior

#

The analysis of Deep Equilibrium Models (DEQ) through the lens of Neural Collapse (NC) reveals interesting insights into DEQ’s representational capabilities, especially under imbalanced data conditions. Theoretically, DEQ exhibits NC under balanced datasets, mirroring the behavior of traditional explicit networks. However, under imbalanced settings, DEQ demonstrates advantages. Unlike explicit networks that often suffer from minority class collapse, DEQ shows a more robust feature convergence. The theoretical analysis provides conditions under which DEQ’s extracted features converge to the vertices of a simplex equiangular tight frame, aligning with classifier weights. This superior behavior in imbalanced scenarios highlights DEQ’s potential for handling real-world data, where class imbalances are common. Empirical validation on CIFAR-10 and CIFAR-100 datasets confirms these theoretical findings, showcasing DEQ’s improved performance and robustness compared to its explicit counterparts.

Imbalanced DEQ

#

In the context of deep equilibrium models (DEQ), handling imbalanced datasets presents a unique challenge. Standard DEQ training might struggle to adequately represent minority classes due to their limited data. A thoughtful approach would involve modifications to the DEQ architecture or training process to address class imbalance. Strategies such as data augmentation, cost-sensitive learning, or incorporating a re-weighting scheme could help balance the influence of different classes during training. Furthermore, theoretical analysis of the impact of class imbalance on DEQ’s convergence properties and generalization ability is crucial. Analyzing whether DEQ retains its memory efficiency and competitive performance under imbalanced conditions is critical. Finally, empirical evaluation on various imbalanced datasets would validate the effectiveness of proposed methods, comparing DEQ’s performance against traditional explicit neural networks under similar conditions. The goal is to determine if DEQ maintains its advantages or exhibits unique strengths in addressing imbalanced classification problems.

Theoretical Analysis

#

The theoretical analysis section of this research paper would likely delve into a rigorous mathematical framework to support the claims made regarding the Deep Equilibrium Model (DEQ) and its behavior under both balanced and imbalanced datasets. It would likely leverage tools from optimization theory, matrix analysis, and potentially other areas of mathematics. Key aspects of the theoretical analysis would center on establishing convergence properties of DEQ’s iterative process, particularly in proving the existence and convergence to a fixed point under well-defined conditions. Another critical component would involve the rigorous study of Neural Collapse (NC) phenomenon, demonstrating mathematically how DEQ exhibits NC under balanced settings and analyzing the deviations from NC under imbalanced scenarios. The analysis may include establishing upper and lower bounds on loss functions to prove DEQ’s superior performance compared to explicit neural networks in certain situations. Furthermore, the analysis should provide a formal mathematical treatment of the conditions under which DEQ exhibits the observed advantages in imbalanced settings. The theoretical arguments will likely involve the exploration of the geometric properties of the learned features and classifier weights in various scenarios. Mathematical proofs and theorems are expected to be a central part of this section, forming the cornerstone of the paper’s credibility and providing strong support for the experimental findings.

Experimental Setup

#

The “Experimental Setup” section of a research paper is crucial for reproducibility and understanding the methodology. It should detail all aspects of the experiments, enabling others to replicate the results. Key elements include a description of the datasets used, their preprocessing steps (if any), model architectures, hyperparameters and their selection process (e.g., grid search, random search, Bayesian optimization), the training procedure (e.g., optimizer, learning rate schedule, batch size, early stopping criteria), evaluation metrics, and hardware and software used. The level of detail should be sufficient for another researcher to conduct the same experiment independently. Clear reporting of hardware specifications is important for assessing computational efficiency, and the reproducibility of experiments is significantly enhanced through open-source availability of code and datasets. A comprehensive and precise experimental setup description ensures the work’s credibility and contributes to the advancement of scientific knowledge.

Future Work

#

The paper’s conclusion mentions future research directions, suggesting several avenues for extension. Extending the analysis beyond simple imbalanced scenarios and linear DEQ models is crucial. Exploring more complex imbalanced settings and nonlinear DEQs would provide a more robust understanding. Investigating the impact of different solver algorithms and their effect on NC phenomenon is another key direction, as is analyzing the generalization performance of DEQs under NC. Furthermore, a comparative study encompassing a wider range of implicit networks and the integration of DEQs with other architectures could reveal further insights. Finally, empirical validation on larger and more diverse datasets, beyond CIFAR-10 and CIFAR-100, is necessary to confirm the broader applicability and generalizability of the theoretical findings.

More visual insights

#

More on figures

This figure compares the learned features from Explicit Neural Networks and Deep Equilibrium Models (DEQ) under imbalanced settings using the CIFAR-10 dataset. The left side shows the results from Explicit Neural Networks, while the right depicts the DEQ results. Two visualizations are provided: t-SNE results showing feature distribution and a Gram matrix visualization (HHT) illustrating the similarity between feature vectors. The comparison highlights the differences in feature representation between the two models, especially under imbalanced data conditions, showing how DEQ handles imbalanced datasets better than the explicit method.

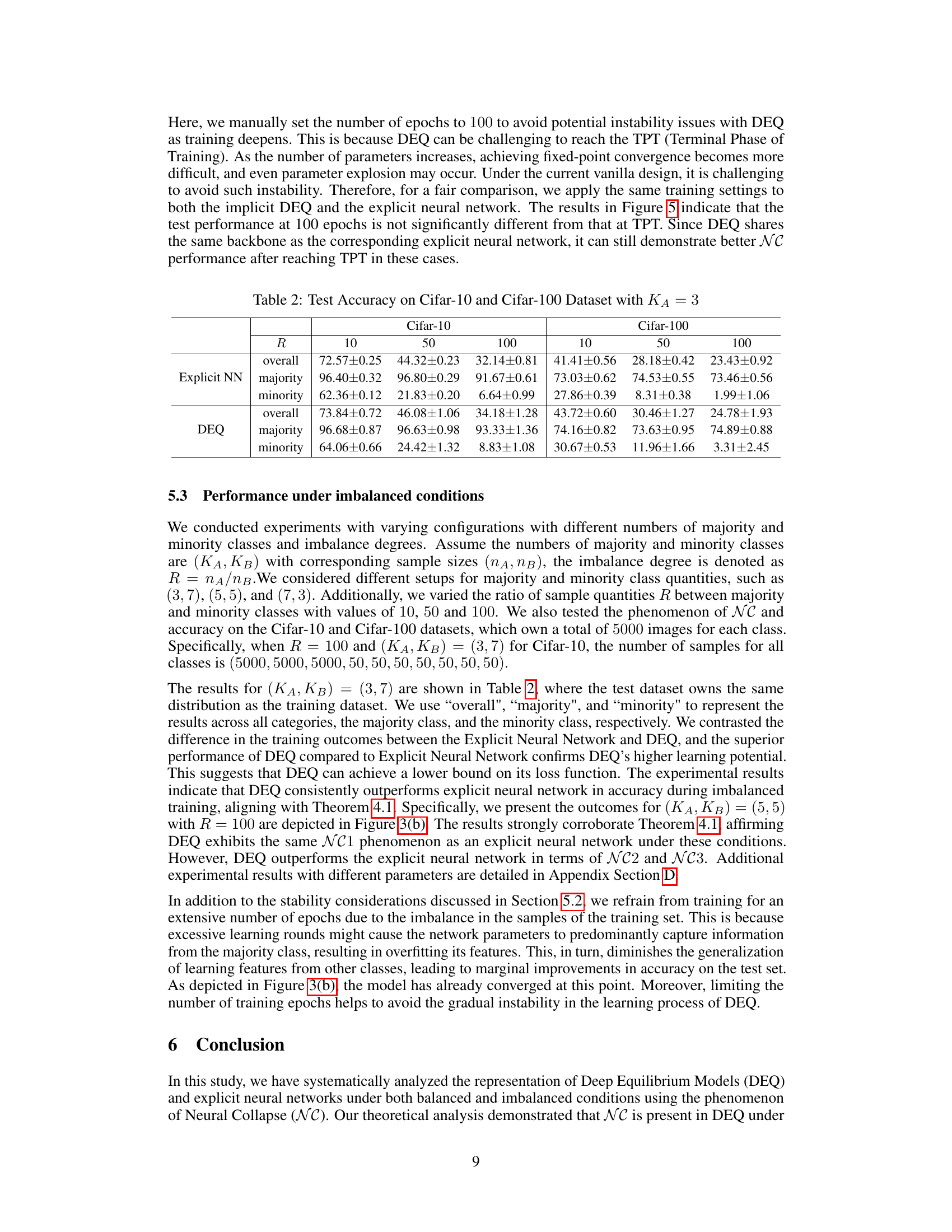
This figure compares the performance of Deep Equilibrium Models (DEQ) and ResNet-18 on CIFAR-10 datasets under both balanced and imbalanced conditions. The plots show accuracy, and three Neural Collapse (NC) metrics (NC1, NC2, NC3) over training epochs. It demonstrates that DEQ outperforms ResNet-18, especially in imbalanced scenarios.

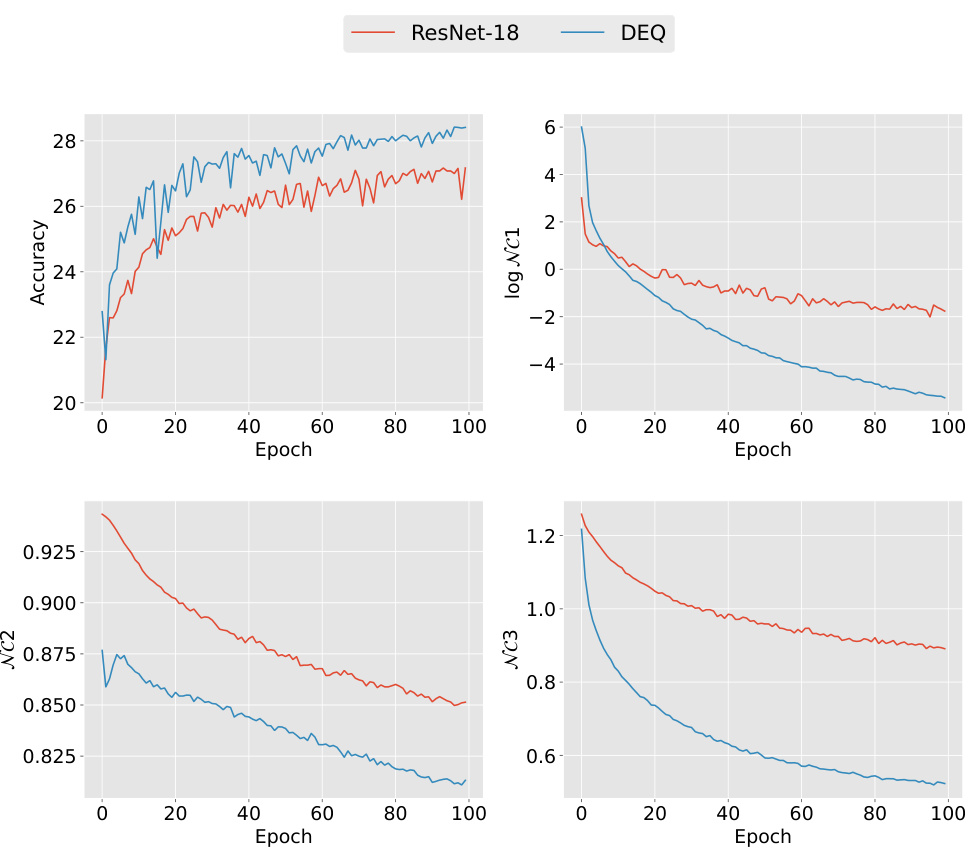
This figure compares the performance of Deep Equilibrium Models (DEQ) and ResNet-18 on CIFAR-10 datasets under both balanced and imbalanced conditions. It illustrates the accuracy and Neural Collapse (NC) metrics (NC1 and NC3) over training epochs for both models. The results show that DEQ outperforms ResNet-18 particularly in imbalanced settings.

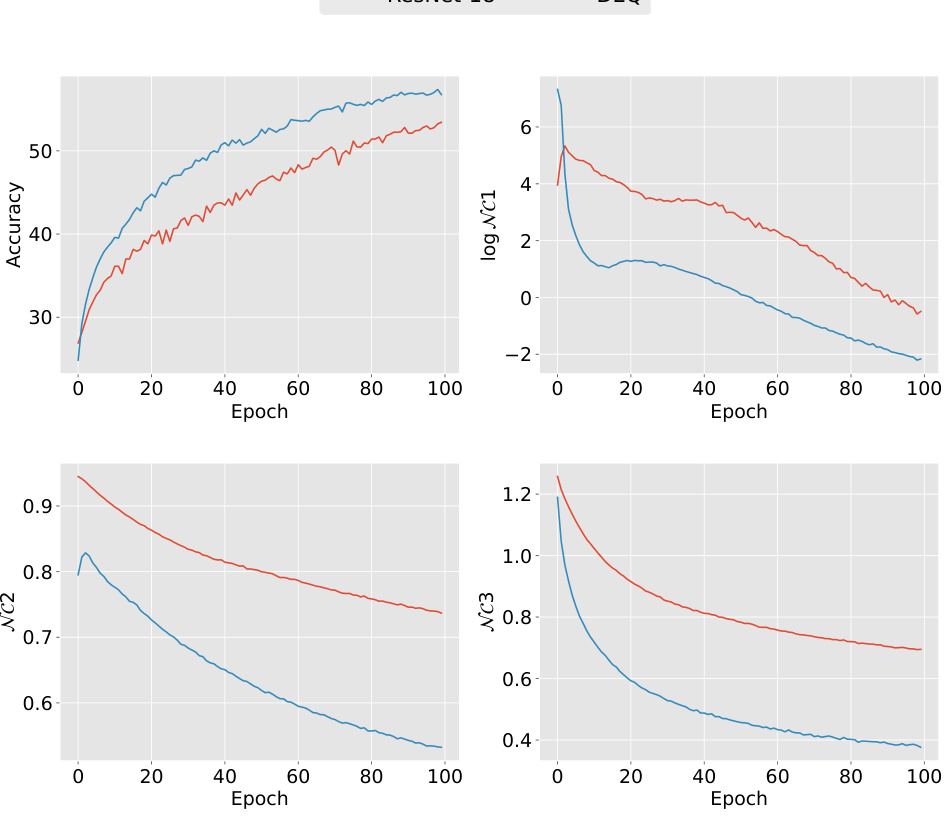
This figure compares the performance of DEQ and ResNet-18 models on CIFAR-10 dataset under both balanced and imbalanced conditions. It shows that DEQ outperforms ResNet-18, especially under imbalanced conditions, in terms of accuracy and Neural Collapse metrics. The results are consistent with previous research.

More on tables

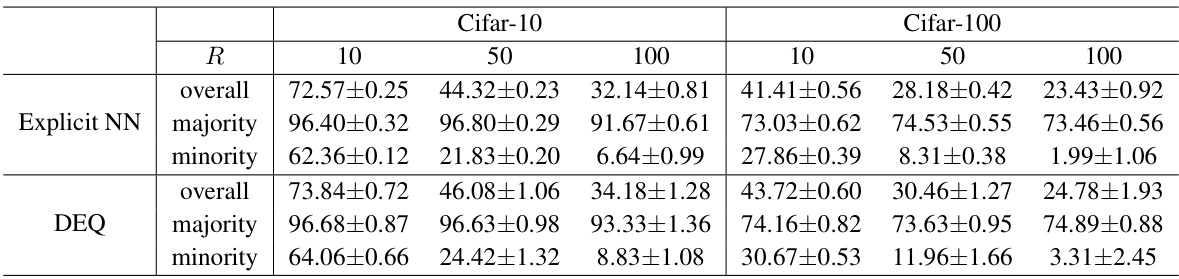
This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets for an imbalanced setting where the number of majority classes is fixed at 3 (KA=3). The results are broken down by overall accuracy, majority class accuracy, and minority class accuracy for different ratios (R=10, 50, 100) of majority to minority class samples. The table compares the performance of both Explicit Neural Networks and Deep Equilibrium Models (DEQ), showcasing DEQ’s potential for better performance on imbalanced datasets.

This table presents the test accuracy results for CIFAR-10 and CIFAR-100 datasets using two different models: Explicit Neural Network and DEQ. The experiments were conducted with varying degrees of class imbalance (R = 10, 50, 100) and different numbers of majority classes (K_A = 5). The results are broken down into overall accuracy, accuracy on majority classes, and accuracy on minority classes for each model and imbalance setting. This allows for a detailed comparison of the two models’ performance across various degrees of class imbalance.

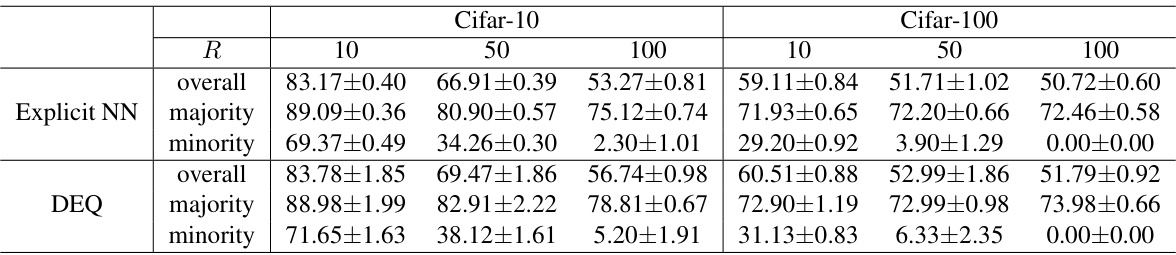
This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets for different imbalance ratios (R=10, 50, 100) when the number of majority classes is 7 and the number of minority classes is 3. The results are shown for both Explicit NN and DEQ models, with overall accuracy, majority class accuracy, and minority class accuracy reported separately for each model and imbalance ratio.

Full paper

#