TL;DR#
Learning to defer (L2D) aims to combine model predictions with expert knowledge, improving accuracy by delegating uncertain predictions. However, directly optimizing the L2D loss function is computationally expensive, requiring surrogate loss functions that facilitate optimization. Previous research proposed several surrogate losses with varying consistency guarantees, but none satisfied all desired properties simultaneously. Specifically, realizable H-consistency, Bayes-consistency and H-consistency bounds were not achieved in previous works.
This paper introduces a broad family of surrogate loss functions for L2D, parameterized by a non-increasing function. The authors prove that these functions achieve realizable H-consistency under mild conditions. Furthermore, for classification error cost functions, these losses admit H-consistency bounds. Notably, the paper resolves an open question regarding a previous surrogate loss function, proving both its realizable H-consistency and Bayes-consistency. The authors identify specific choices of the parameter function that lead to H-consistent surrogate losses for any general cost function, achieving the desired consistency properties simultaneously. Empirical results demonstrate that these proposed surrogate losses are either comparable or superior to existing baselines across various datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in machine learning, particularly those working on learning to defer (L2D). It provides a comprehensive framework for designing surrogate loss functions with strong theoretical guarantees, addressing limitations of prior work and opening new avenues for research in this critical area. The results have significant implications for improving the efficiency and reliability of L2D systems across diverse applications.
Visual Insights#
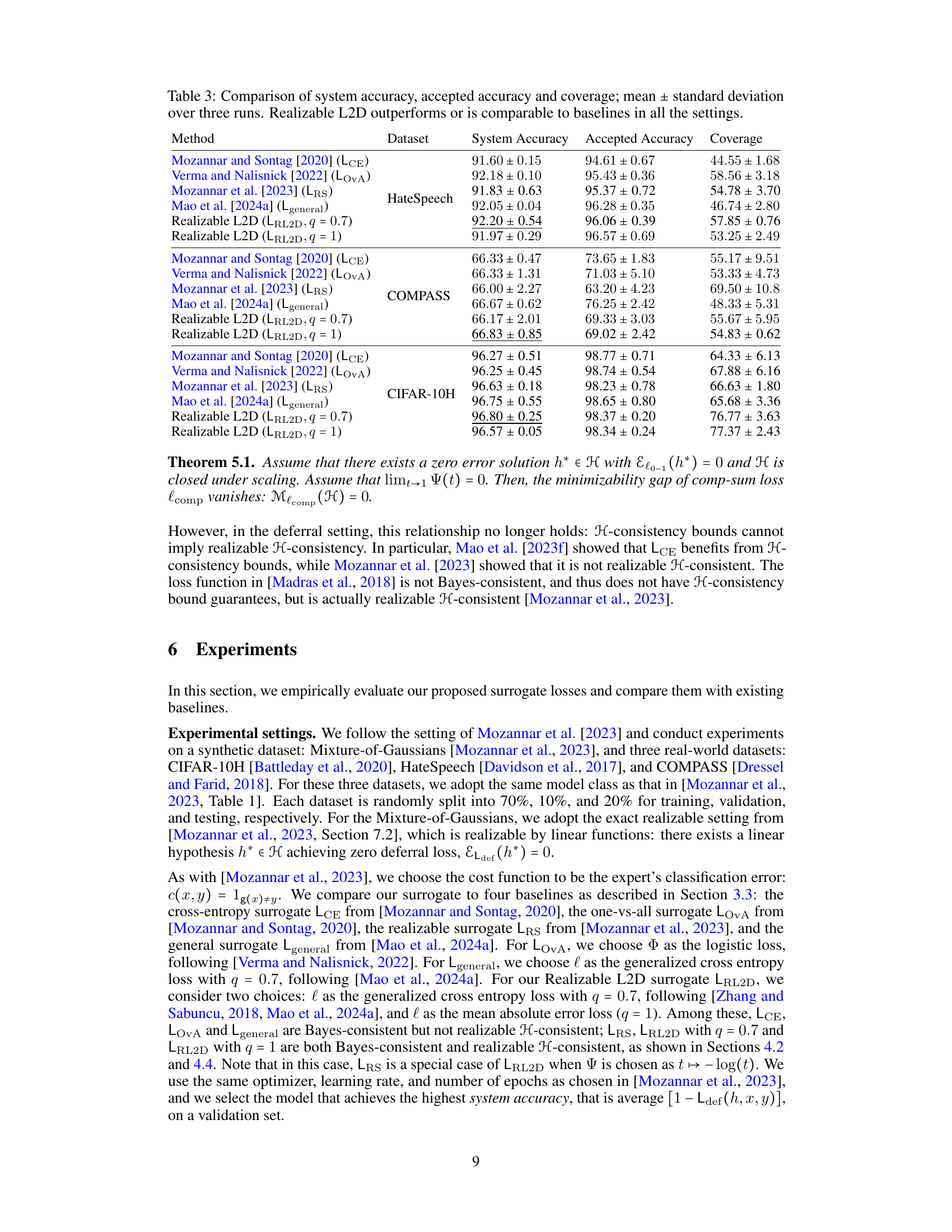
🔼 This figure presents the results of experiments comparing the performance of various surrogate loss functions in learning to defer scenarios. Figure 1a shows system accuracy versus the training sample size on a realizable synthetic dataset (Mixture-of-Gaussians). This plot demonstrates that the proposed surrogate losses (LRL2D, q=0.7 and q=1) which are theoretically realizable H-consistent significantly outperform existing surrogate losses (LCE, LOVA, Lgeneral). Figure 1b shows system accuracy versus coverage on the HateSpeech dataset with general cost functions. It illustrates that as the inference cost (β) increases, the coverage of deferral methods increase while system accuracy decreases. The proposed LRL2D losses perform similarly to other Bayes-consistent methods.
read the caption
Figure 1: Results for the realizable case and the non-realizable case with general cost functions.
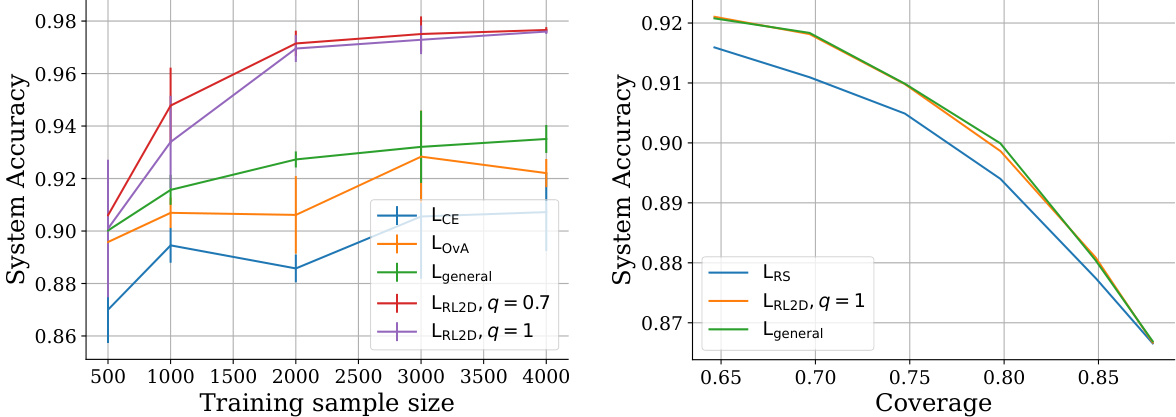
🔼 This table summarizes the consistency properties of several surrogate loss functions for learning to defer, focusing on the case where the cost function is based on the expert’s classification error. It compares existing methods (LCE, LOVA, Lgeneral, LRS) with the newly proposed LRL2D family of losses. For each loss function, the table indicates whether it satisfies realizable H-consistency, Bayes-consistency, and H-consistency bounds. The table highlights the advantages of the LRL2D family in simultaneously achieving multiple consistency guarantees.
read the caption
Table 2: Consistency properties of existing surrogate losses and ours in the case of c(x, y) = 1g(x)+y.
In-depth insights#
Surrogate Loss Study#
A surrogate loss study in the context of a machine learning research paper would deeply investigate various loss functions used as substitutes for the true, often intractable, loss function. This involves a theoretical analysis of consistency properties, such as Bayes-consistency and H-consistency (and its variants), to determine how well a surrogate loss approximates the true loss. The study would rigorously assess the convergence guarantees of the proposed methods and possibly provide bounds on the generalization error. It would also consider the computational aspects of the surrogate loss functions, their compatibility with various optimization algorithms, and their performance in different scenarios or datasets. A comprehensive evaluation across multiple experiments would be crucial to validate the theoretical findings and demonstrate the practical effectiveness of the surrogate loss approach. Empirical results, such as system accuracy, accepted accuracy, and coverage, would be presented and compared to baselines. Finally, a proper analysis of the limitations, along with potential avenues for future work, such as extensions to multi-expert settings or two-stage learning, would round off the investigation.
H-Consistency Bounds#
The concept of “H-consistency bounds” in machine learning offers a crucial refinement to the notion of Bayes-consistency. Bayes-consistency ensures that minimizing a surrogate loss function leads to minimizing the true risk, but only asymptotically and over all possible data distributions. H-consistency bounds, however, provide a more practical guarantee. They establish a relationship, often expressed through a concave function, between the excess risk of the surrogate loss (how much worse than optimal it performs) and the excess risk of the true loss. This means that even with limited data or within a specific hypothesis class (H), achieving low surrogate loss directly translates to low true loss, offering a finite-sample, hypothesis-dependent guarantee of performance. The strength of the bound, governed by the concave function, determines how tightly the surrogate loss approximates the true loss and is a crucial factor in assessing the quality of the surrogate loss. It’s important to note that H-consistency bounds implicitly guarantee Bayes-consistency since the bounds hold for all distributions. Understanding and deriving these bounds are central to designing effective surrogate loss functions in various learning scenarios.
Bayes Consistency#
Bayes consistency, in the context of surrogate loss functions for learning to defer (L2D), is a crucial concept signifying that minimizing the surrogate loss also minimizes the true deferral loss. A Bayes-consistent surrogate loss ensures that the learning process converges to the optimal decision strategy, even when directly optimizing the complex deferral loss is intractable. This property is particularly important in L2D because the true deferral loss function often involves the expert’s error and deferral costs, making direct optimization computationally challenging. The paper investigates various surrogate loss functions, analyzing their Bayes consistency and highlighting the key challenges in achieving both Bayes consistency and other desirable properties like realizable H-consistency and H-consistency bounds simultaneously. The identification of surrogate losses that satisfy these multiple consistency criteria is a significant contribution, enabling more robust and reliable L2D models. The results highlight that achieving Bayes consistency alone may not suffice, emphasizing the need for stronger guarantees like H-consistency to ensure good generalization performance, especially in complex, real-world scenarios. Therefore, the analysis of Bayes consistency in this paper is not merely a theoretical exercise but a practical necessity for creating effective learning-to-defer algorithms.
L2D Experimental Results#
Analyzing L2D experimental results requires a multifaceted approach. First, dataset selection is crucial: the choice of synthetic versus real-world data significantly impacts the results and generalizability. Real-world datasets introduce noise and complexities absent in synthetic settings. Second, model architecture influences performance. Linear models may be sufficient for some synthetic data but are inadequate for real-world data requiring more complex neural networks. Third, evaluation metrics must be carefully chosen to reflect L2D’s unique challenges. Focusing only on overall accuracy may be misleading, as it overlooks the trade-off between accuracy and deferral rate. Analyzing accepted accuracy and coverage provides a more nuanced understanding of model performance. Finally, comparison to baselines is vital for establishing the value of the proposed L2D approach. Showing improved results compared to established methods across various metrics offers stronger evidence of the approach’s effectiveness.
Future L2D Research#
Future research in learning to defer (L2D) should prioritize handling more complex scenarios, such as multi-expert systems and two-stage settings, where multiple experts offer opinions or the model iteratively refines predictions. Robustness to noisy or unreliable expert feedback is crucial. Additionally, exploring theoretical guarantees beyond current H-consistency and Bayes-consistency is essential for general cost functions, addressing limitations like minimizability gaps. Practical application-driven research is needed to validate L2D’s efficacy in diverse domains, along with addressing bias and fairness issues, ensuring equitable outcomes across demographics. Finally, developing efficient algorithms capable of handling large-scale datasets and complex models remains a critical direction for future development of L2D techniques.
More visual insights#
More on tables

🔼 This table summarizes the consistency properties of different surrogate loss functions for learning to defer in the specific case where the cost function is based on the expert’s classification error. It shows whether each loss function satisfies realizable H-consistency, Bayes-consistency, and H-consistency bounds. The table compares the properties of existing losses (LCE, LOVA, Lgeneral, LRS) with the newly proposed losses (LRL2D with various choices of function Ψ).
read the caption
Table 2: Consistency properties of existing surrogate losses and ours in the case of c(x, y) = 1g(x)+y.
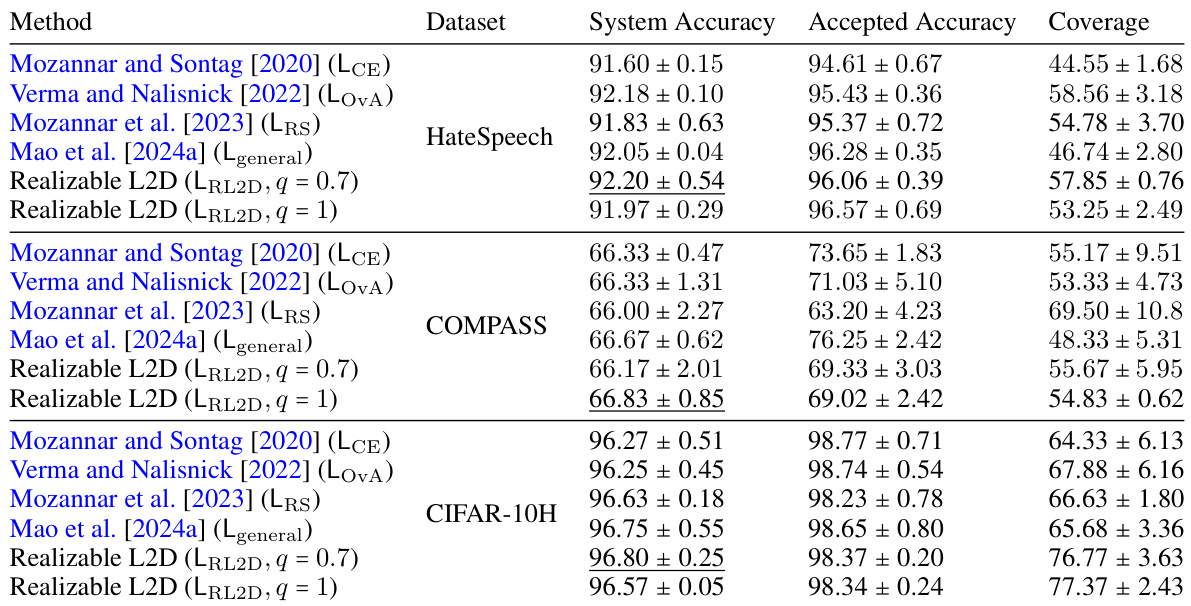
🔼 This table compares the performance of several learning-to-defer (L2D) methods, including those proposed in the paper, across three real-world datasets. For each method and dataset, it shows the system accuracy (overall accuracy), accepted accuracy (accuracy on non-deferred instances), and coverage (percentage of instances not deferred). The results demonstrate the effectiveness of the proposed Realizable L2D methods compared to existing baselines.
read the caption
Table 3: Comparison of system accuracy, accepted accuracy and coverage; mean ± standard deviation over three runs. Realizable L2D outperforms or is comparable to baselines in all the settings.
Full paper#