↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
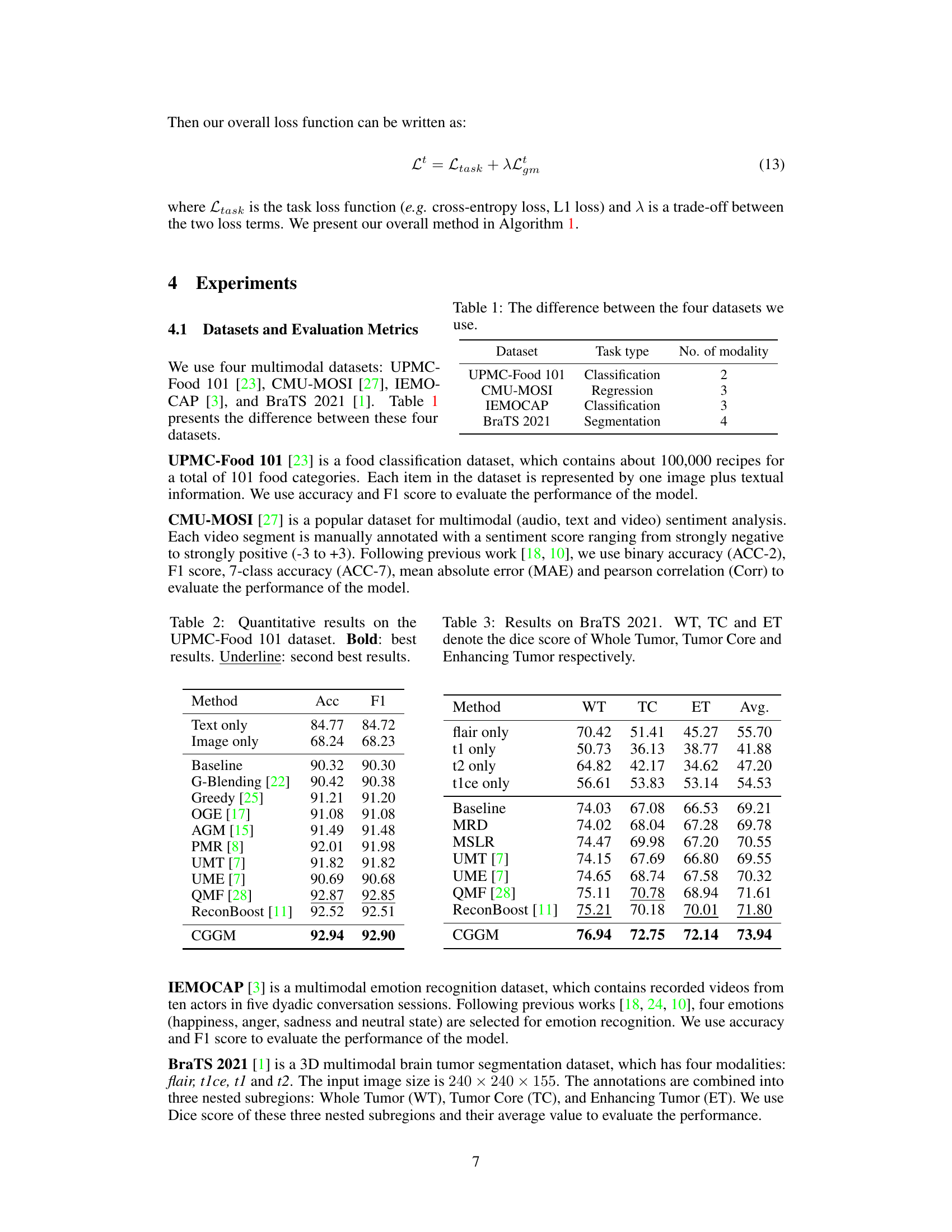
Multimodal learning, while promising, often suffers from the issue of models overly relying on one modality. Existing methods addressing this limitation have shortcomings, focusing on gradient magnitude and ignoring direction, or being restricted in task types and the number of modalities. This paper introduces a new method, CGGM (Classifier-Guided Gradient Modulation), which tackles this problem.
CGGM uses classifiers to evaluate each modality’s contribution. It then modulates the gradient magnitudes and directions of each encoder using modality-specific utilization rates derived from the classifiers. Extensive experiments on four multimodal datasets (covering classification, regression, and segmentation) showcase that CGGM consistently outperforms state-of-the-art methods, demonstrating its versatility and effectiveness.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and versatile method, CGGM, for balancing multimodal learning. CGGM addresses the common issue of multimodal models over-relying on a single modality, improving the overall performance and generalizability of such models. This is particularly relevant given the increasing use of multimodal data in various fields. The results on multiple datasets and tasks demonstrate CGGM’s effectiveness and open up avenues for further research in this active area.
Visual Insights#

This figure illustrates the architecture of the Classifier-Guided Gradient Modulation (CGGM) method. It shows how multiple modalities are processed independently by encoders (Φ1, Φ2, … ΦM), then fused by a fusion module (Ω). Crucially, classifiers (f1, f2,… fM) are included during training to evaluate the individual contribution of each modality and adjust the gradient updates accordingly. The classifiers compute the utilization rate of each modality (direction) and the speed of improvement (magnitude) to guide the update of both modality-specific encoders and the fusion module, ensuring balanced multimodal learning. During inference, the classifiers are discarded for efficiency.
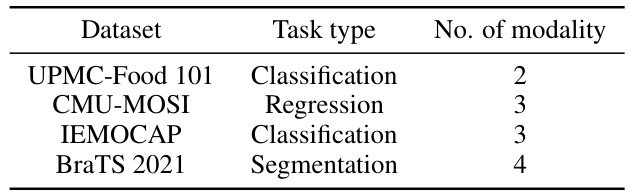
This table summarizes the key differences among the four multimodal datasets used in the paper’s experiments. It shows the dataset name, the type of task (classification, regression, or segmentation), and the number of modalities involved for each dataset. This information is crucial for understanding the diversity and scope of the experimental evaluation.
In-depth insights#
Multimodal Imbalance#
Multimodal imbalance in machine learning signifies a scenario where the model heavily favors one modality over others during training, leading to suboptimal performance. This imbalance hinders the effective integration of diverse information sources, such as text, images, and audio, ultimately limiting the model’s ability to generalize and make accurate predictions. Factors contributing to this imbalance include differences in data quality, volume, and noise levels across modalities. A dominant modality might learn faster, overshadowing less prominent ones. This issue is particularly challenging when modalities have varying levels of information richness and relevance to the task. Addressing multimodal imbalance requires careful consideration of data preprocessing techniques, appropriate fusion strategies, and possibly specialized loss functions or training algorithms that explicitly handle differences in modality contributions. Techniques like gradient modulation and data augmentation tailored to the specific modalities can help mitigate this problem. Ultimately, achieving balanced multimodal learning is crucial for building robust and accurate models capable of leveraging the full potential of diverse information sources.
Gradient Modulation#
Gradient modulation techniques in multimodal learning aim to address the issue of imbalanced learning, where some modalities dominate the training process, hindering the effective use of others. These methods typically involve adjusting the gradients of different modalities during backpropagation. Simple magnitude adjustments, such as scaling or clipping, can improve balance, but more sophisticated approaches consider the direction of the gradients. By influencing both magnitude and direction, these methods encourage a more balanced learning process, allowing the network to fully exploit the information present in all modalities. Classifier-guided gradient modulation is particularly promising as it offers an adaptive approach, using classifier outputs to guide the modulation, dynamically adjusting the learning process to enhance utilization of weaker modalities. Success depends on careful consideration of hyperparameters, such as the scaling factor applied to the gradient. However, this technique is potentially computationally expensive compared to simpler approaches, demanding additional resources for the classifiers used in the modulation process.
CGGM Method#
The Classifier-Guided Gradient Modulation (CGGM) method is a novel approach to address the issue of imbalanced multimodal learning, where a model might overly rely on a single dominant modality during training. CGGM tackles this by considering both the magnitude and direction of gradients, a more comprehensive approach compared to existing methods which often focus solely on gradient magnitude. Classifiers are strategically integrated to evaluate each modality’s contribution, providing a dynamic mechanism to modulate gradients according to the utilization rate of each modality. This ensures that under-optimized modalities receive a boost, while preventing the dominant modalities from overshadowing others. The resulting improved balance leads to more effective multimodal learning and improved performance, demonstrated across various tasks including classification, regression, and segmentation tasks on multiple datasets. This sophisticated methodology shows promise for enhancing the efficiency of multimodal learning and utilizing information from different modalities comprehensively.
Experimental Results#
A thorough analysis of the experimental results section requires understanding the research question, methodology, and metrics used. The choice of datasets is crucial, reflecting the generalizability of the approach. The paper should clearly state how the results demonstrate the effectiveness of the proposed method compared to baselines or existing techniques. Statistical significance of the results needs to be established through appropriate methods. Are there limitations in the experimental setup, and how might they affect the interpretation of findings? A visualization of the results is essential to facilitate understanding and reveal trends. Specific metrics for evaluating performance, including precision, recall, F1-score, or accuracy, along with error bars or confidence intervals, bolster the credibility of the findings. Finally, an in-depth discussion of unexpected or interesting results that deviate from expectations contributes to the paper’s strength.
Future Works#
Future research directions stemming from this Classifier-Guided Gradient Modulation (CGGM) method should prioritize addressing its computational limitations. Reducing the reliance on additional classifiers, perhaps through more efficient gradient estimation techniques, is crucial for broader applicability. Investigating the method’s robustness across a wider variety of multimodal tasks and datasets, including those with highly imbalanced data or noisy modalities, is essential. Exploring the impact of different fusion strategies and their interaction with CGGM is another promising area. Finally, a theoretical analysis to formally establish the conditions under which CGGM guarantees convergence and optimality would strengthen its foundation. Comparative studies against other advanced balancing methods are also needed to better understand CGGM’s unique strengths and limitations within the broader multimodal learning landscape.
More visual insights#
More on figures
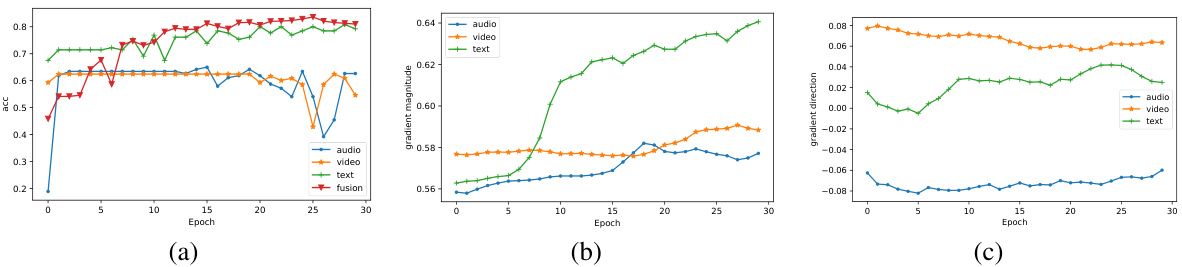
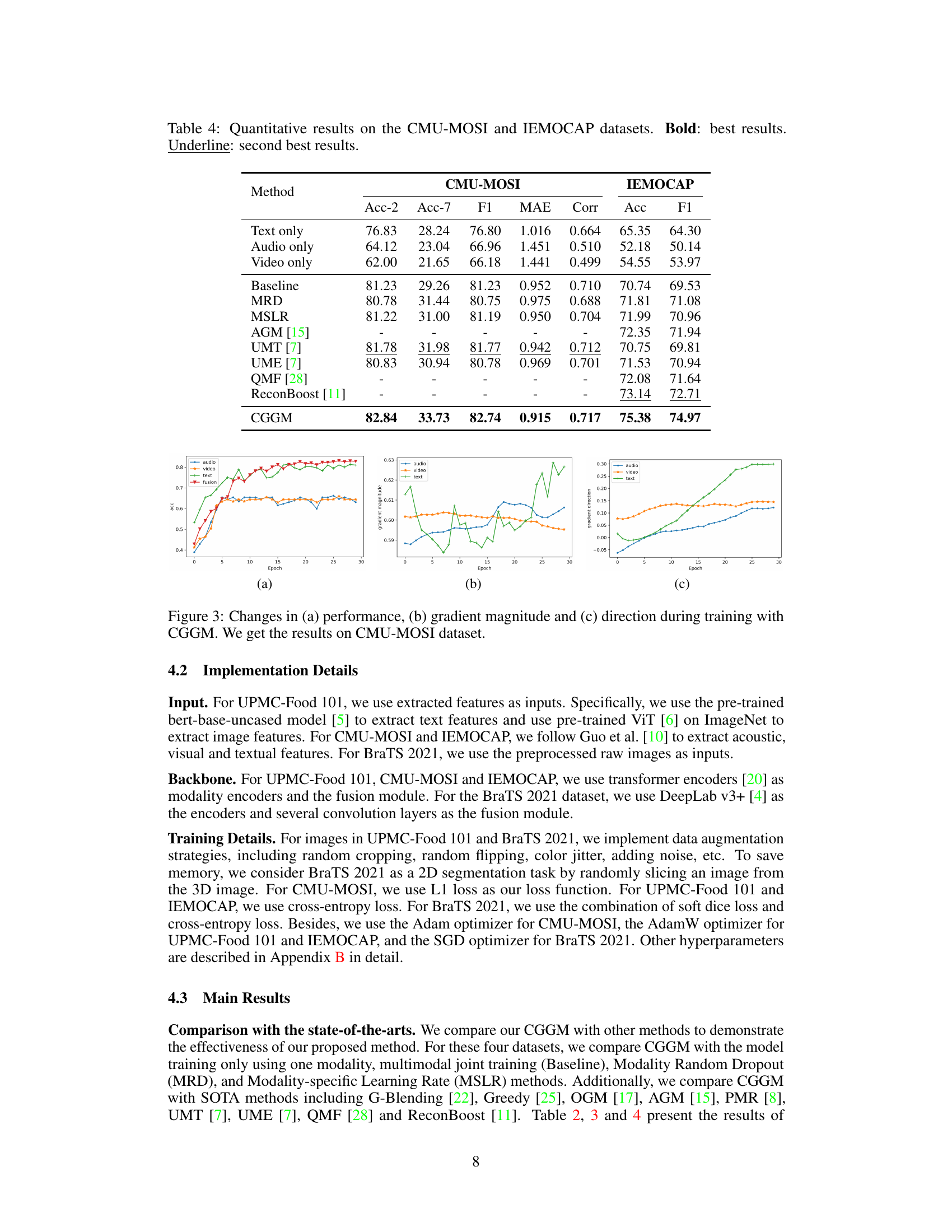
This figure shows the analysis of gradient during the training process on the CMU-MOSI dataset. (a) shows the accuracy of each modality (audio, video, text) and their fusion over epochs. (b) displays the gradient magnitude of each modality, using the Euclidean norm of the gradient vector. (c) illustrates the gradient direction similarity between each modality and the fusion using cosine similarity.

This figure displays three graphs that illustrate the training process of a multimodal model using the CMU-MOSI dataset. Graph (a) shows the accuracy of each modality (audio, video, text) and the fusion of all modalities over training epochs. Graph (b) illustrates the gradient magnitude for each modality and fusion. Graph (c) depicts the cosine similarity between each modality’s gradient and the fused gradient, showing the alignment of gradients during training.
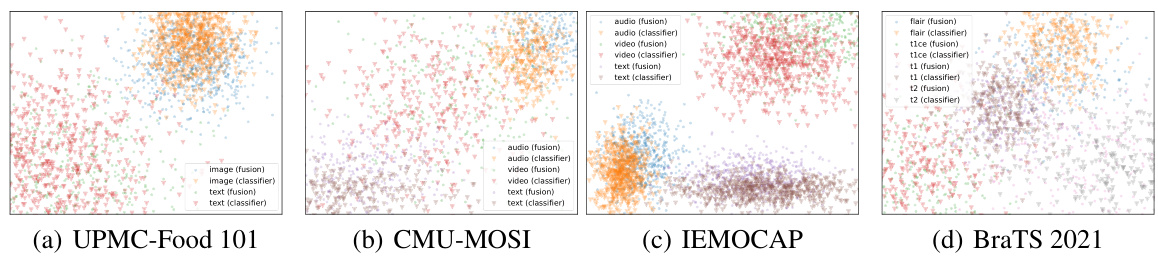
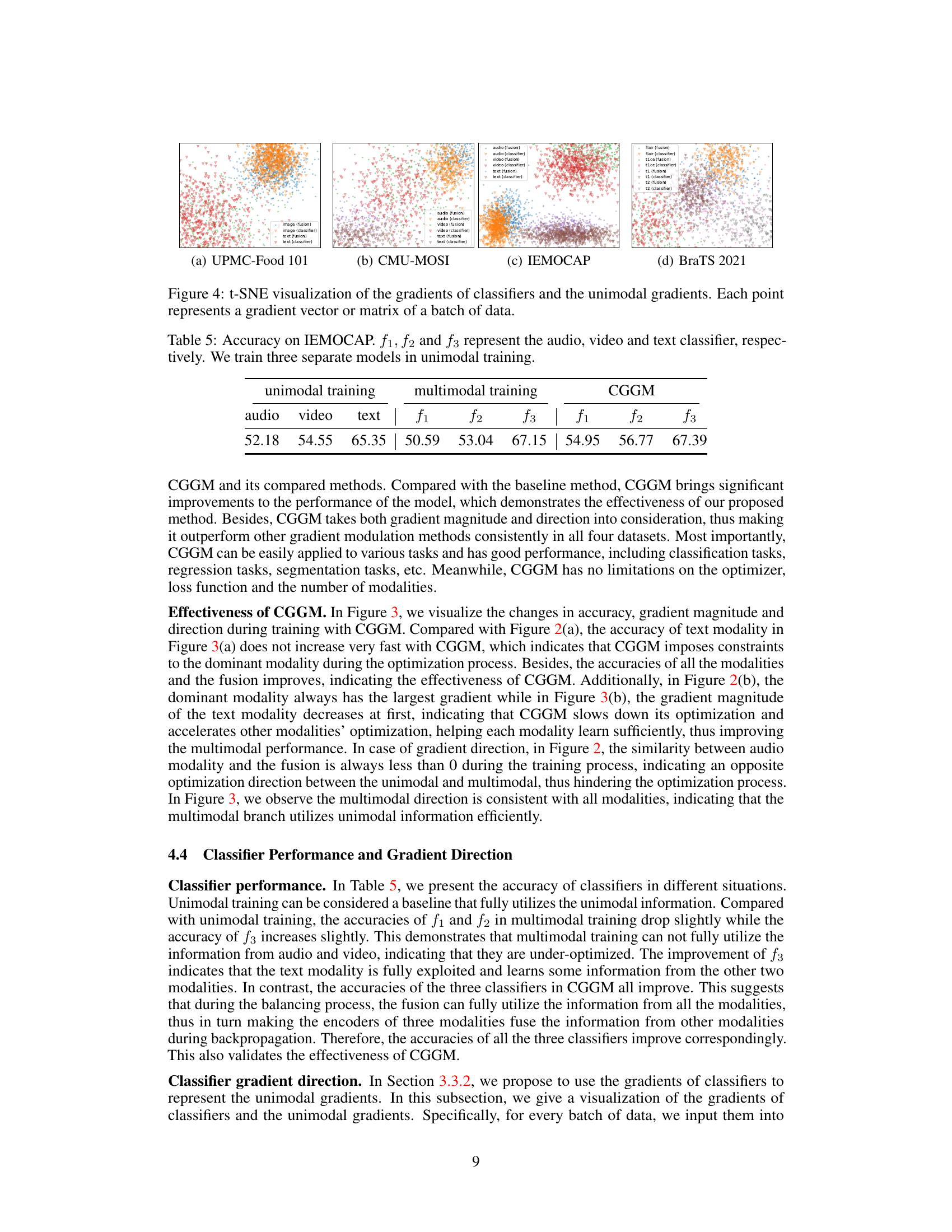
This figure visualizes the gradients of classifiers and unimodal gradients using t-SNE for dimensionality reduction. Each point in the plots represents a gradient vector or matrix from a batch of data. The plots compare the gradients obtained from the classifiers (which provide a prediction based on a single modality) to the gradients calculated for the fusion module, which integrates information from all modalities. The proximity of points suggests the similarity of the gradients. This visualization helps to demonstrate the relationship between classifier gradients and the corresponding gradients used in the multimodal learning model, supporting the claim that classifier gradients can effectively represent unimodal gradients.

This figure shows the ablation study results for hyperparameters (p) and (\lambda) in the proposed CGGM method. Subfigure (a) demonstrates the effect of varying the scaling hyperparameter (p) on accuracy and F1 score, showing an optimal range for (p) that maximizes performance. Subfigure (b) illustrates the effect of varying the loss trade-off hyperparameter (\lambda) on accuracy and F1 score, revealing an optimal range for (\lambda) that balances task performance and gradient modulation. Both subfigures use bar graphs to present the improved performance compared to a joint training baseline, highlighting the importance of carefully tuning these parameters for optimal CGGM performance.

This figure visualizes the changes in model performance (accuracy), gradient magnitude, and gradient direction during the training process using the proposed Classifier-Guided Gradient Modulation (CGGM) method. The results are specifically shown for the CMU-MOSI dataset. It demonstrates how CGGM affects the learning dynamics across different modalities. Panel (a) shows accuracy changes over epochs, while (b) and (c) illustrate the changes in the magnitude and direction of gradients, respectively. The comparison highlights the balancing effect of CGGM on the learning process.

The figure shows the changes of balancing term during the training process with and without CGGM. The balancing term is used to modulate the gradient magnitude and direction to balance the training process. From the figure, we can observe that when CGGM is used, the balancing term of each modality fluctuates around 0, indicating that the training process is balanced. When CGGM is not used, the balancing term of the dominant modality is always greater than 0, indicating that the dominant modality is over-optimized.
More on tables
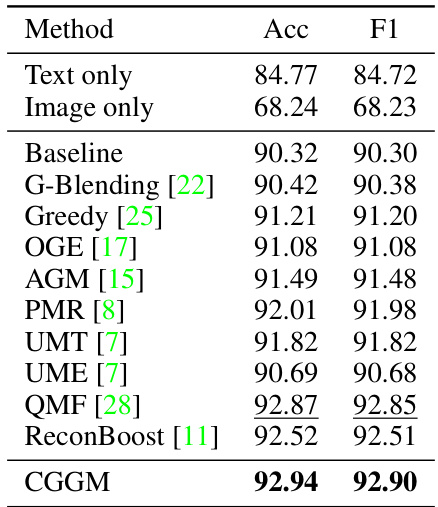
This table presents a quantitative comparison of different methods on the UPMC-Food 101 dataset, showing their accuracy and F1 score. The best and second-best results are highlighted for easy comparison. The methods include using a single modality (text or image), a baseline multimodal approach, and several state-of-the-art multimodal learning methods. The table helps illustrate the effectiveness of the proposed CGGM method.

This table presents the quantitative results of the BraTS 2021 dataset. It compares various methods, including baselines and state-of-the-art approaches, in terms of their performance on three subregions of brain tumors: Whole Tumor (WT), Tumor Core (TC), and Enhancing Tumor (ET). The average Dice score across these three regions is also provided for each method. The Dice score is a common metric for evaluating the accuracy of segmentation models.

This table presents a comparison of the performance of several methods (including the proposed CGGM) on two benchmark multimodal datasets: CMU-MOSI and IEMOCAP. For CMU-MOSI, which is a regression task, the metrics shown are accuracy (Acc-2 and Acc-7), F1 score, mean absolute error (MAE), and Pearson correlation (Corr). For IEMOCAP, a classification task, the metrics are accuracy (Acc) and F1 score. The best result for each metric is bolded, and the second-best is underlined. The results highlight the relative strengths of each method across different multimodal tasks.

This table presents the accuracy results of the IEMOCAP dataset for different training methods. The first three columns show accuracy using individual modalities (unimodal training), the next three columns show accuracy when training with all modalities simultaneously (multimodal training), and the final three columns show accuracy when training with all modalities and using the proposed CGGM method. f1, f2, and f3 represent the accuracy of the audio, video, and text classifiers, respectively. It demonstrates the performance improvement achieved using CGGM over unimodal and multimodal training.

This table presents the ablation study results on the IEMOCAP dataset to demonstrate the effectiveness of modulating gradient magnitude and direction in the proposed CGGM method. It compares the baseline model with three variants of CGGM: one modulating only the magnitude (p=1.0, λ=0), one modulating only the direction (p=None, λ=0.1), and one modulating both (p=1.0, λ=0.1). The results show that modulating both gradient magnitude and direction yields the best performance, indicating the complementarity of these two strategies in balancing multimodal learning.
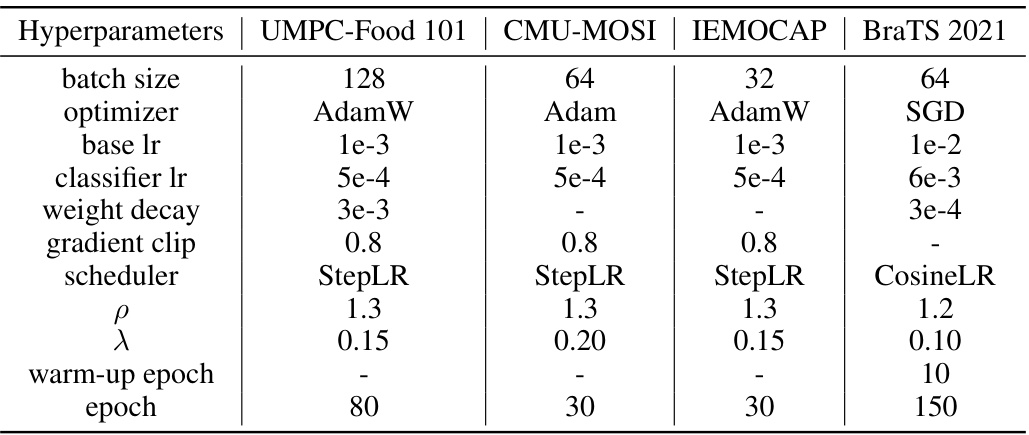
This table lists the main hyperparameters used in the experiments performed on four different multimodal datasets: UPMC-Food 101, CMU-MOSI, IEMOCAP, and BraTS 2021. These hyperparameters include the batch size, optimizer, base learning rate, classifier learning rate, weight decay, gradient clipping value, learning rate scheduler, ρ (a scaling hyperparameter for gradient magnitude modulation), λ (a trade-off parameter between task loss and balancing term), warm-up epochs, and total training epochs. The specific values used for each parameter varied across the different datasets to optimize performance for each specific task.

This table shows the additional GPU memory cost in MB for using classifiers in the proposed CGGM method across four different datasets: UPMC-Food101, CMU-MOSI, IEMOCAP, and BraTS. The memory overhead is relatively small, ranging from 8MB to 24MB, depending on the dataset.
Full paper#